浅埋大断面矩形顶管掘进面稳定性及支护压力分析

俞 淼，刘 维，史培新，贾鹏蛟

(苏州大学 轨道交通学院，江苏 苏州 215000)

矩形顶管因具有断面利用率高、施工扰动小等优点，被越来越多地应用于城市地下工程建设中，并向着大断面、长距离顶进的趋势发展.浙江嘉兴“南湖号”下穿南湖大道工程[1]中，矩形顶管机断面宽14.800 m，高9.426 m，顶程超过100.000 m，是目前世界上断面最大的矩形顶管机.随着地下空间的飞速发展，大断面超浅埋工程逐渐增多，在施工中如出现操作不当，更易引发掌子面失稳，进而导致地表沉降过大甚至塌陷，给施工安全带来了较大挑战.例如内蒙古科技大学地下通道工程[2]中，由于支护压力不够，引起掘进面失稳，造成沉降过大，影响工程的施工安全.因此，有必要研究浅埋大断面矩形顶管掘进面的稳定性及支护压力.

针对掘进面稳定性的理论研究，S.JANCSECZ等[3]提出了三维楔形体模型，基于极限平衡法推导了极限支护压力表达式.W.BROERE[4]将计算模型扩展到成层土条件，分析了土压及泥水平衡盾构施工极限支护压力.G.ANAGNOSTOU[5]研究了土拱效应对隧道开挖面稳定性的影响，优化了计算模型及支护压力的表达式.许有俊等[6]研究了砂砾石地层条件下矩形顶管开挖面的稳定性，利用梯形楔形体模型推导出开挖面主动破坏极限支护压力表达式.程诚等[7]假设破坏区域为一弧形楔形体，基于筒仓理论，推导出干砂条件下开挖面主动极限支护力计算公式.LIN Y.等[8]基于极限平衡法，提出了考虑无支护长度的三维对数-螺旋棱柱体模型，用以分析砂土中浅埋隧道掘进面的稳定性.E.LECA等[9]提出了三维锥体模型，基于上限法推导出极限支护压力表达式.LIU W.等[10-11]使用上限分析法建立了局部被动失稳模型，用以分析盾构掘进过程中的掘进面稳定性，利用模型试验分析了隧道工作面移动速度对其稳定性的影响.S.SENENT等[12]利用平面三角块体和螺旋块体共同构建失稳机动模型，研究了隧道开挖步距对掘进面稳定性影响.数值与模型试验方面，李奥等[13]利用基于盾构隧道开挖面模型试验和数值模拟，得到失稳破坏模式，提出了修正棱柱楔形体模型.周利梅等[14]针对砂性土复杂地层，利用FLAC3D研究了隧道埋深、土体内摩擦角等因素对隧道施工前方土体稳定性的影响.综上，目前研究主要集中于针对圆形盾构及顶管开挖面的稳定性，而有关浅埋大断面矩形顶管开挖面稳定性问题的研究较少.矩形顶管与圆形顶管相比，其掘进面上方土拱效应较弱，因此土体稳定性较差，掘进面更容易失稳.

为此，笔者以苏州轨道交通5号线某车站附属地下工程为依托，对掘进面稳定性展开研究.对传统楔形体模型进行优化，考虑土拱效应增加，并优化模型的几何参数，使其更接近真实情况.同时，根据优化模型计算极限支护压力最优解，并与传统模型极限支护压力计算结果进行对比.最后结合工程现场数据，对优化模型进行验证.

1 工程概况

本研究的依托工程为苏州市轨道交通5号线某车站附属地下工程.该工程地处主干道交叉路口，下穿金鸡湖大道，道路下面的市政管线密集，因此工程设计采用矩形顶管施工.图1为工程平面图.顶管掘进长度约62.8 m，共42环管节，始发井位于北侧，向南掘进直至接收井，采用钢平台进行接收.始发井端头采用三重管旋喷桩及三轴搅拌桩进行加固，接收端头采用MJS桩加固.

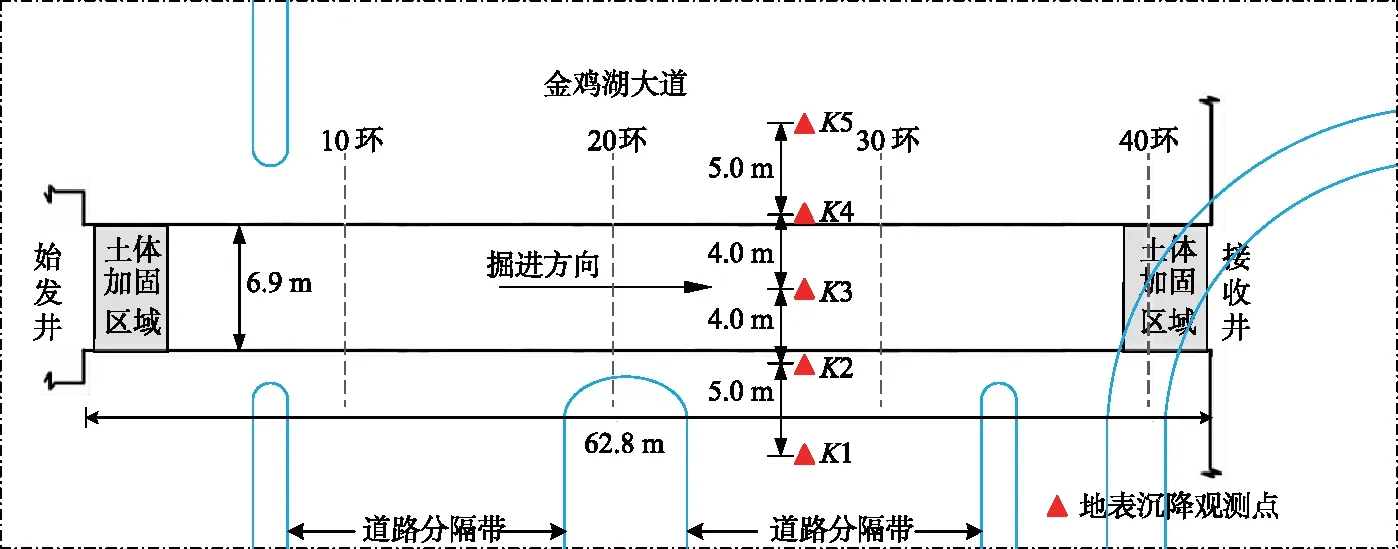
图1 工程平面图

图2为工程剖面图.在图2中，管节外截面尺寸为6.9 m×4.2 m，覆土深度约为4.5 m.顶管主要穿越的土层包括填土层(①1)和粉质黏土层(③1)，下卧土层为黏质粉土夹粉质黏土层(③3).地下水水位埋深约为地表以下2.0 m.各土层的物理力学性质参数如表1所示.

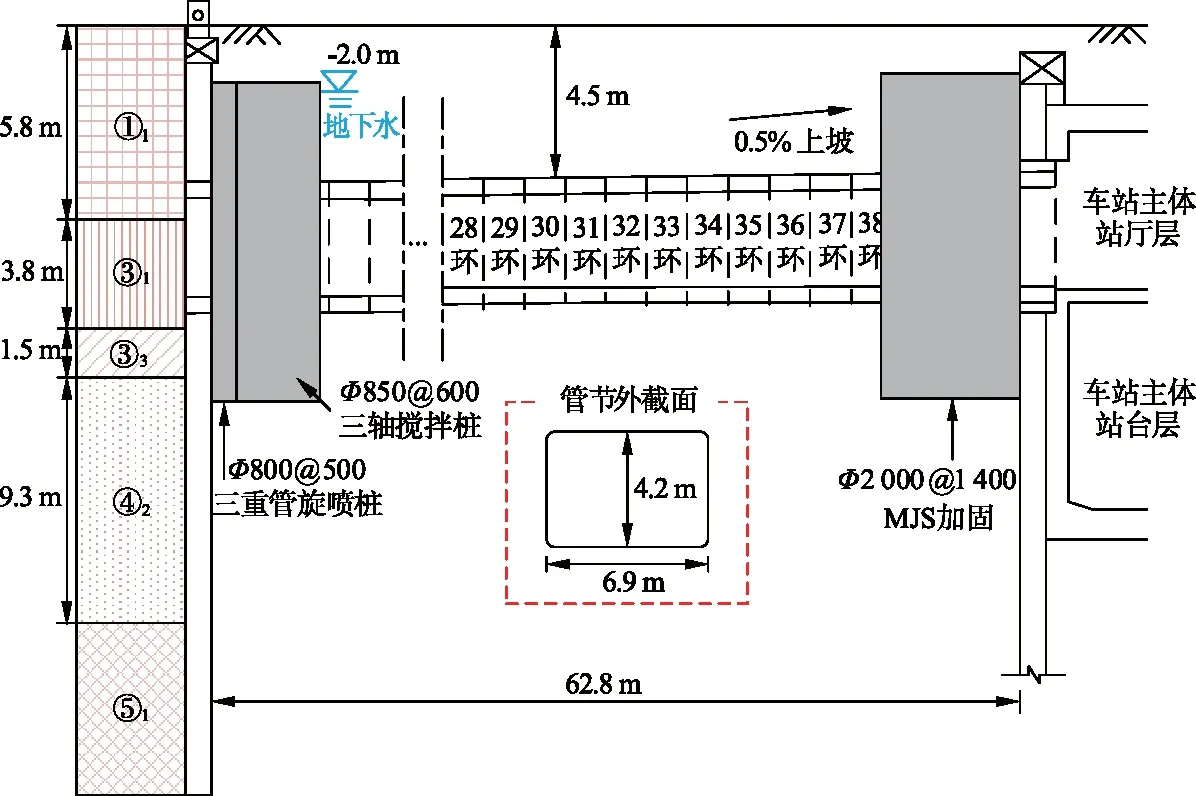
图2 工程剖面图

表1 各土层物理力学性质参数

基于穿越土层信息、顶管埋深以及穿越主干道的沉降控制要求，选用尺寸为6.9 m×4.2 m多刀盘土压平衡式矩形顶管机.顶管机断面切削率大于80%，且对称分布，掘进时动态稳定性易控制，满足施工需要.顶管机截面的现场刀盘布置实物图如图3所示.多刀盘土压平衡式矩形顶管机配件及其参数如表2所示.

图3 现场刀盘布置

表2 矩形顶管机配件及其参数

2 沉降监测

监测断面布置的观测点处地表沉降变化情况如图4所示，其中K1与K5、K2与K4分别距顶管轴线9、4 m，对称布置，K3位于轴线正上方(见图1).掘进面位置为工程的掘进面与监测断面之间的直线距离.

图4 地表沉降监测情况

由图4可知，监测断面各观测点沉降曲线规律近似，随着掘进面与监测断面距离增大，地表沉降呈现出明显的阶段性特征，且沉降值随距轴线距离增加而减小.掘进面位置为-3.0～0 m时，沉降明显增大，其中K3监测点沉降绝对值由6.6 mm突增至9.0 mm.施工进程显示，顶管掘进至28环时停机时间较长，保压能力弱，因而产生了较大的地表沉降.

土压力传感器布置示意图如图5所示.土压力传感器监测到的相关土压力值如表3所示.监测结果表明施工造成沉降过大的现象，其原因是开仓进行清障处理，此阶段土压力值减小，这与掘进面稳定性有一定的关联.地表沉降过大是由于变形不断增大，而变形的快速发展可能会导致掘进面失稳，因此有必要对掘进面稳定性展开研究.

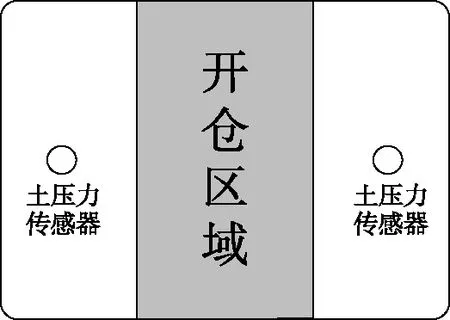
图5 土压力传感器布置示意图

表3 传感器监测的土压力值

3 掘进面稳定性理论分析

3.1 矩形顶管掘进面受力分析

矩形顶管掘进面受力简化模型如图6所示.

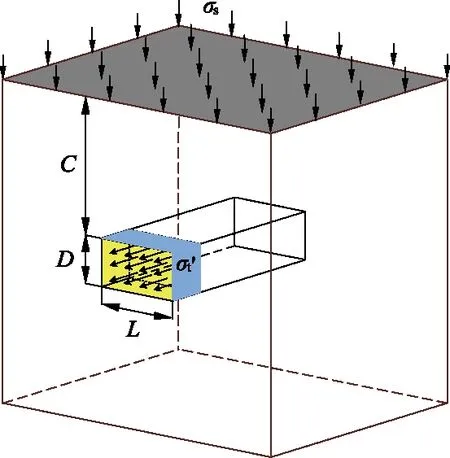
图6 矩形顶管掘进面受力简化模型

假设地层为均质地层，且符合Mohr-Coulomb破坏准则.矩形顶管断面长、宽分别为L、D，埋深为C，有效支护压力σt′均匀作用于掘进面上，隧道上方地表荷载为σs.土体的有效重度为γ′，有效黏聚力为c′，有效内摩擦角为φ′.

3.2 优化模型

传统筒仓模型由与工作面齐平的楔形体和上覆地层土柱组成.实际工程中由于存在卸荷拱，土体破坏范围会更小.因此有必要对传统筒仓模型进行改进.图7为优化后的梯形楔形体模型.

图7 优化后的梯形楔形体模型

假设开挖面失稳时滑动块形状为一个等腰梯形楔形体，滑块上部为一个梯形棱柱.楔形体顶面等腰梯形底角为α，滑动面与水平方向夹角为θ，隧道工作面宽度为L，高度为D，隧道埋深为C.掘进面前方土体破坏区域由L、D、θ和α共同决定.

图8为楔形体的受力示意图.由图8可知，滑动块上的作用力如下：① 上方棱柱体垂直作用于楔形体顶面befc上的作用力Pv；② 底部滑动面adfc上的摩擦阻力T和法向作用力N，T作用方向为沿ac方向斜向上，N垂直作用于面adfc上；③ 分别作用于侧向滑动面abc和def之上的摩擦力Ts和法向作用力Ns，Ts沿平行于ac方向斜向上，Ns分别垂直于面abc和面def；④ 作用于开挖面abed上有效支护力S，方向为沿着y轴正方向；⑤ 土体自重G.

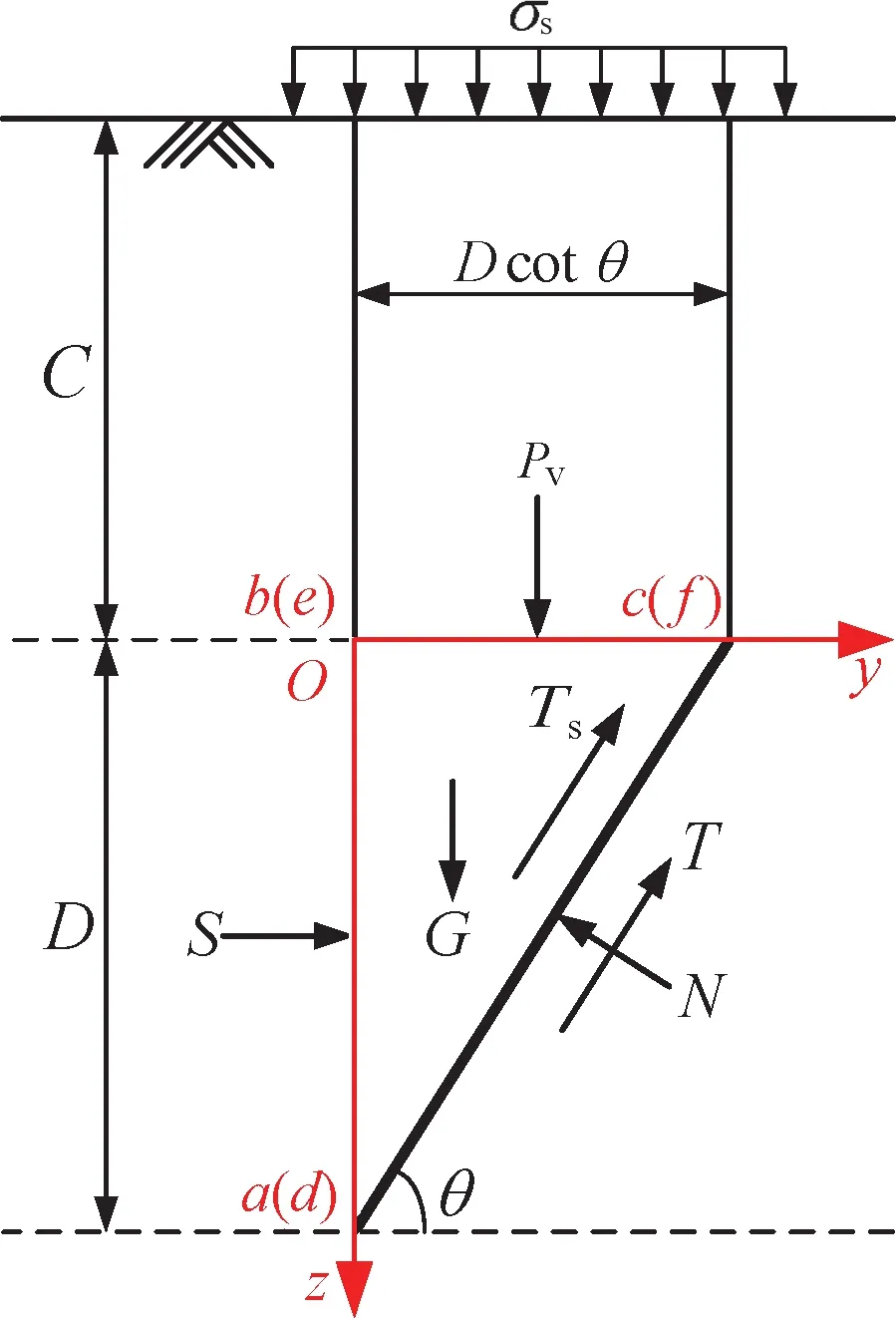
图8 楔形体受力示意图

下面对楔形体所受作用力进行推导.

1)上方棱柱体垂直作用于楔形体顶面befc上的作用力Pv.计算式如下：

(1)

式中：σv为滑动块顶部所受的竖向应力，考虑了土拱效应，用太沙基松动土压力公式[4]进行计算：

(2)

式中：λ为土体侧压力系数，计算式为λ=1-sinφ′[13]；σs为地表荷载；R为上覆土柱的体积与侧面积的比值[4]，即

(3)

2)作用于底部滑动面adfc的摩擦阻力T.计算式如下：

(4)

3)楔形体两侧滑动面作用力Ts和Ns.图9为楔形体侧面受力示意图.图10为楔形体受力俯视图.如图9、10所示，取掘进面上边界be中点作为坐标原点O.

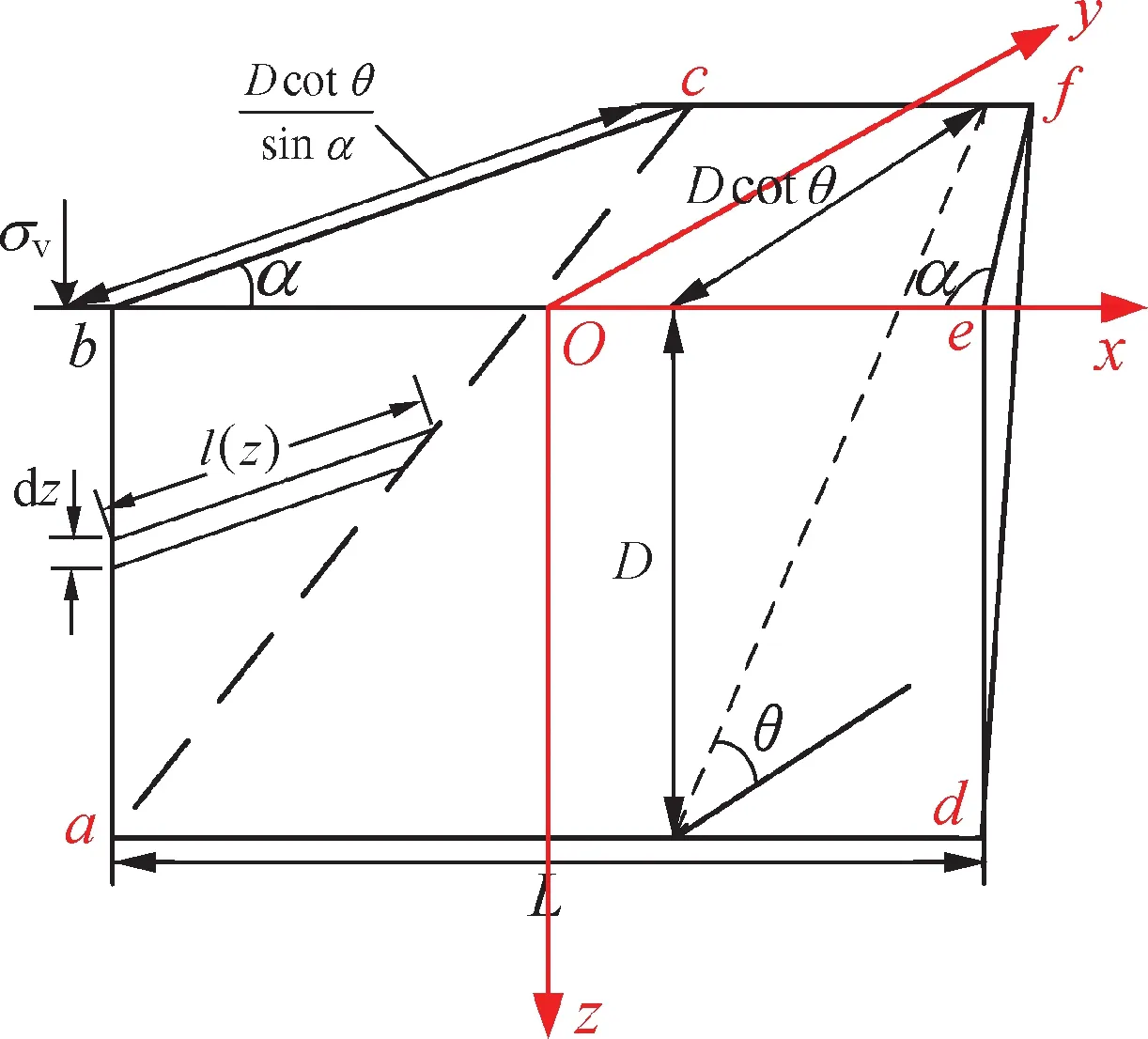
图9 楔形体侧面受力示意图

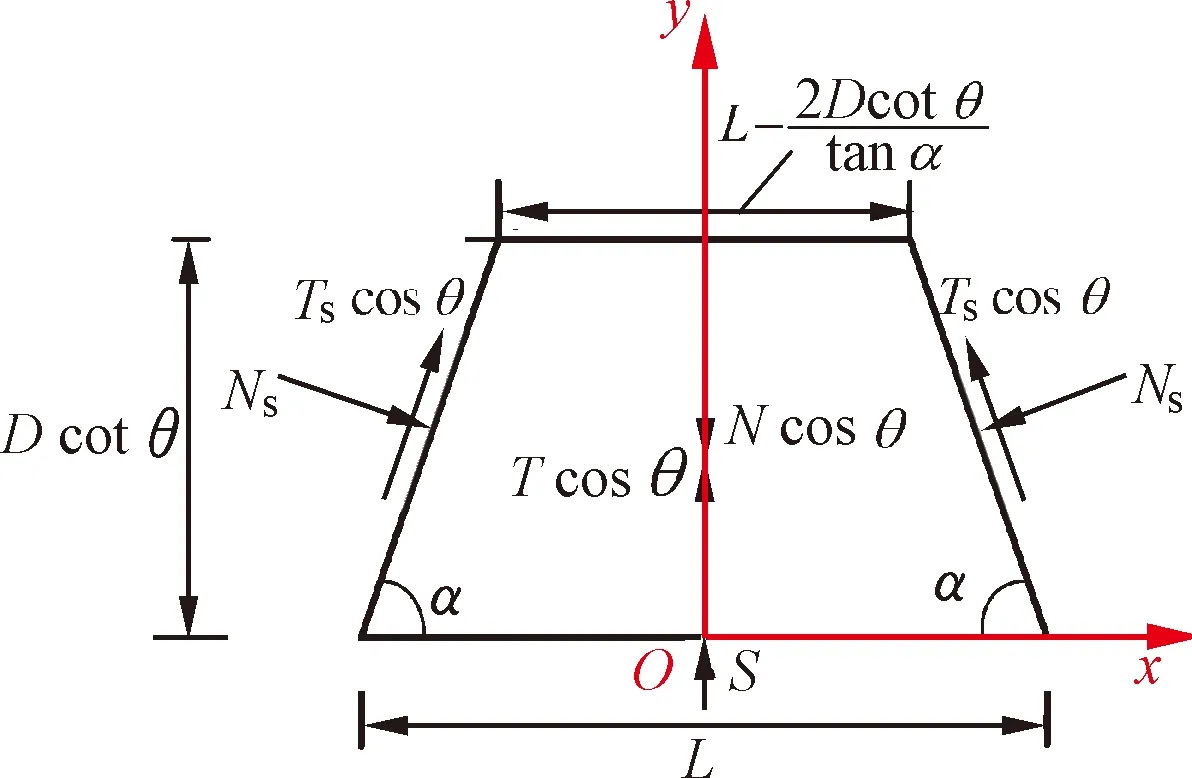
图10 楔形体受力俯视图

假设楔形体的侧向滑动面受到的竖向土压力沿埋深方向呈线性增加，则埋深为z处的竖向土压力σz为

(5)

其中竖向应力σv按照式(2)计算.则楔形体滑动块侧面法向作用力Ns为

(6)

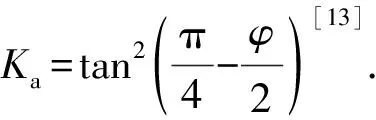
沿三角形截面的摩擦力Ts为

(7)

其中σz按式(5)计算.

4)土体自重G.计算式如下：

(8)

式中：V为楔形体体积，

(9)

由y轴方向受力平衡得

S+2Nscosα=Nsinθ-(T+2Ts)cosθ.

(10)

由z轴方向受力平衡得

Pv+G=Ncosθ+(T+2Ts)sinθ.

(11)

联立式(4)、(10)和(11)，得到有效支护压力：

(12)

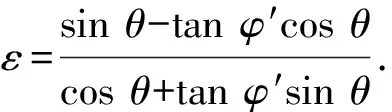
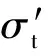
4 极限支护压力分析

4.1 最优破坏模式分析

为了研究模型最优化问题，分析在不同土体强度参数和隧道几何参数条件下最优破坏模式所对应的参数θ、α及破坏区域土体体积V(由公式(9)计算)的变化.假设地表荷载σs=0，D=6.0 m，γ′=9.8 kN·m-3，分别研究土体抗剪强度参数(φ′和c′)与隧道几何参数(C/D和L/D)变化对破坏模式的影响.有效内摩擦角φ′为15°～45°，有效黏聚力c′为0～6 kPa，C/D为0.5～2.0，L/D为1.00～2.00.表4为不同土体抗剪强度下破坏模式参数变化情况.

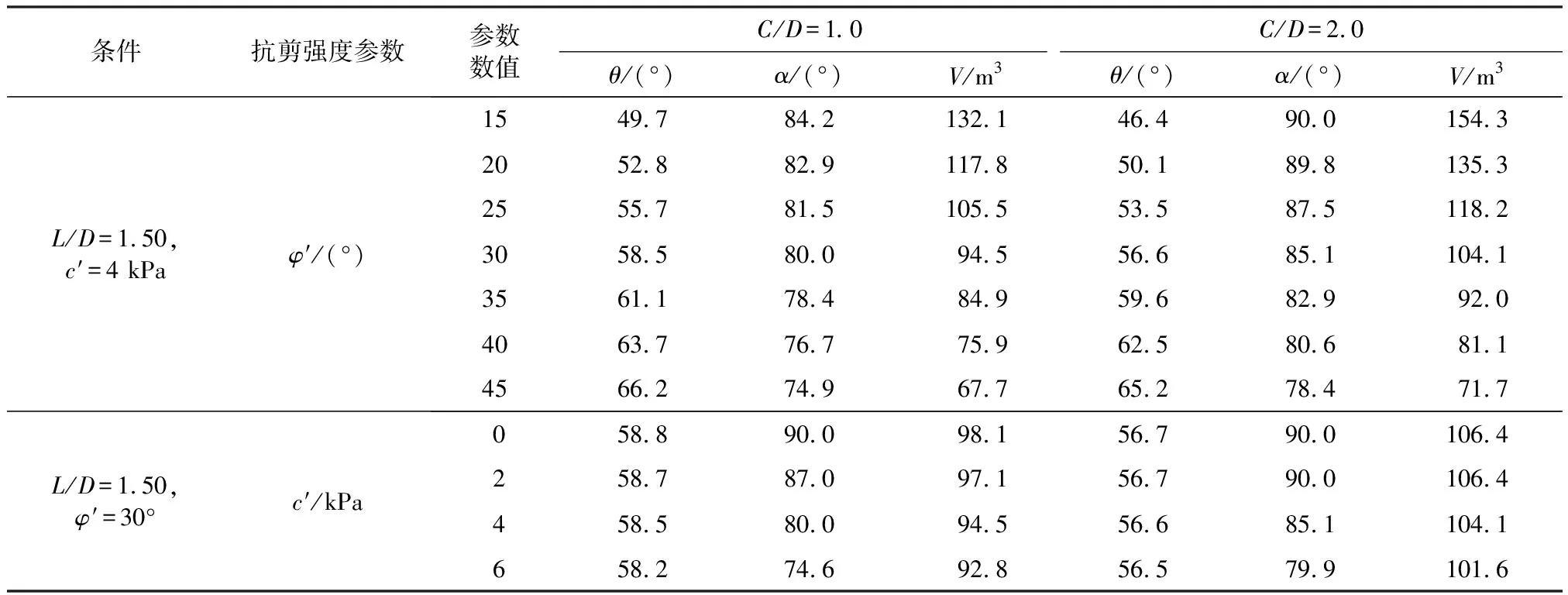
表4 不同土体抗剪强度下破坏模式参数变化情况

由表4可知：给定c′、L/D和C/D时，随着φ′增大，θ逐渐增大，而α逐渐减小，对应是破坏区域体积逐渐减小；当C/D=1.0时，θ从49.7°增加到66.2°，α则从84.2°减小到74.9°，土体破坏区域体积从132.1 m3减小到67.7 m3，减小了约48.8%；给定φ′、L/D和C/D时，随着c′增大，θ逐渐减小，α也逐渐减小，破坏区域体积随之减小.原因在于内摩擦角越大，或者黏聚力越大，抗剪强度增加，自稳能力越强，土体破坏区域就越小.表4中出现了α=90.0°的情况，说明此时修正模型退化到了传统楔形体模型，这是由于土体抗剪强度较低，导致破坏区域较大.

表5为土体抗剪强度参数一定时，破坏模式参数随几何参数变化情况.

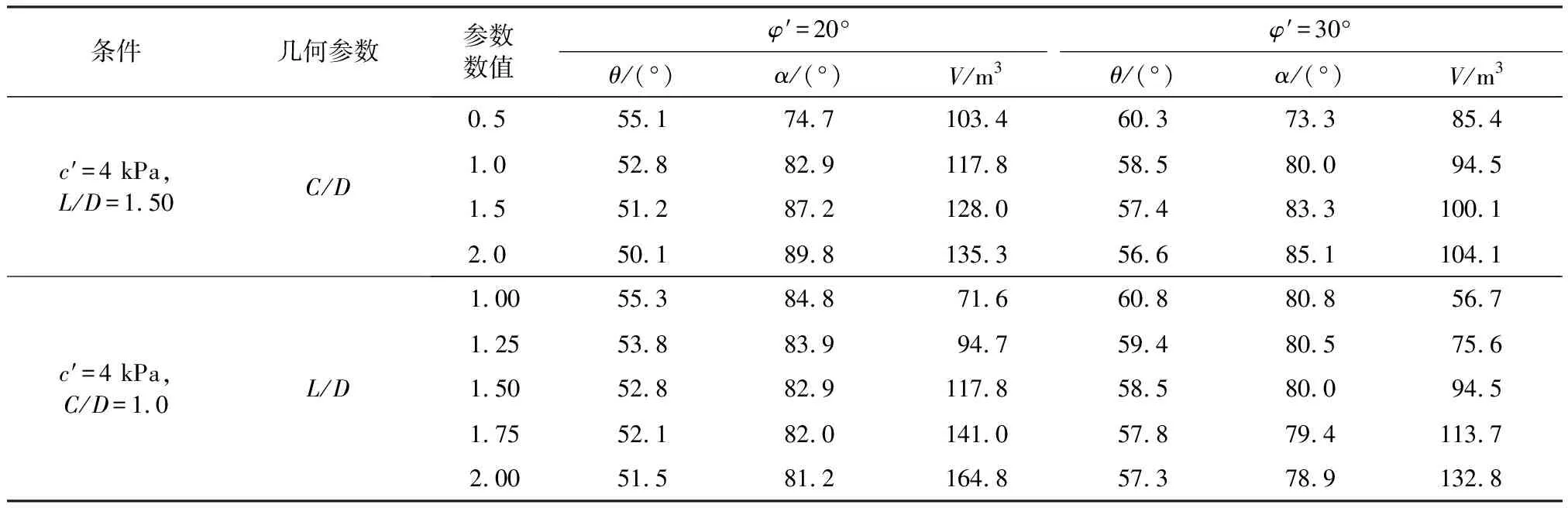
表5 土体抗剪强度参数一定时，破坏模式参数随几何参数变化情况

由表5可知，当给定c′、φ′、L/D时，随着几何参数C/D增大，θ逐渐减小，而α逐渐增大，破坏区域体积随之增大.以φ′=20°为例，θ从55.1°逐渐减小到50.1°，α从74.7°逐渐增大到89.8°，土体破坏区域体积从103.4 m3增加到135.3 m3，破坏区域体积增大了约30.9%.这是因为埋深越大，上覆土压力越大，对掘进面稳定影响越大，土体破坏区域越大.

当给定c′、φ′、C/D时，随着L/D增大，θ减小，α也减小，破坏区域体积随之增大.原因在于工作面宽度增加导致土拱效应减弱，使得上覆土压力增大，土体破坏区域越大.

4.2 极限支护压力参数分析

给定土体抗剪强度参数和隧道几何参数，对极限支护压力影响因素作参数分析，得到了不同条件下最优破坏模式所对应极限支护压力的值.参数取值与上节相同，分别研究土体抗剪强度参数(φ′、c′)与隧道几何参数(C/D、L/D)变化对极限支护压力影响.

1)土体抗剪强度参数.图11为L/D=1.50时极限支护压力与土体抗剪强度参数的关系曲线.图11a中，随着有效内摩擦角的增加，极限支护压力呈非线性减小趋势.当L/D=1.50，C/D=1.0，c′=4 kPa时，有效内摩擦角从15°增加至45°，极限支护压力减小了约88.4%.这是因为有效内摩擦角越大，随着围岩抗剪强度增加，自稳能力越强，维持工作面稳定所需支护压力就越小.

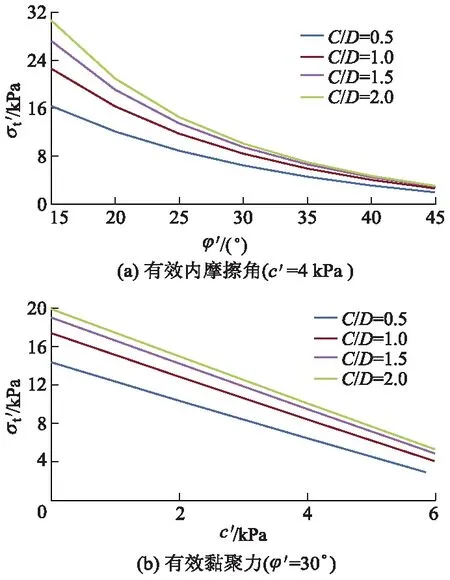
图11 L/D=1.50时，极限支护压力与抗剪强度关系曲线

图11b中，有效黏聚力对极限支护压力影响类似于有效内摩擦角，随着有效黏聚力的增加，极限支护压力呈线性减小趋势.当L/D=1.50，C/D=1.0，φ′=30°时，有效黏聚力从0 kPa增加至6 kPa，极限支护压力减小了约67.9%.原因在于土体抗剪强度增加.

2)隧道几何参数.图12为c′=4 kPa时，极限支护压力与隧道几何参数的关系曲线.图12a中，随隧道埋深与工作面高度比值的增加，极限支护压力呈非线性增加趋势.以φ′=20°为例，C/D从0.5增加至2.0，极限支护压力增加了约72.8%.原因在于埋深越大，上覆土压力增大，所需支护压力就越大.当C/D>1.0时，随着C/D的增加，曲线逐渐趋于平缓，也即极限支护压力变化幅度不明显，这主要由于工作面前方围岩的拱形效应会阻止破坏面延伸至地表.

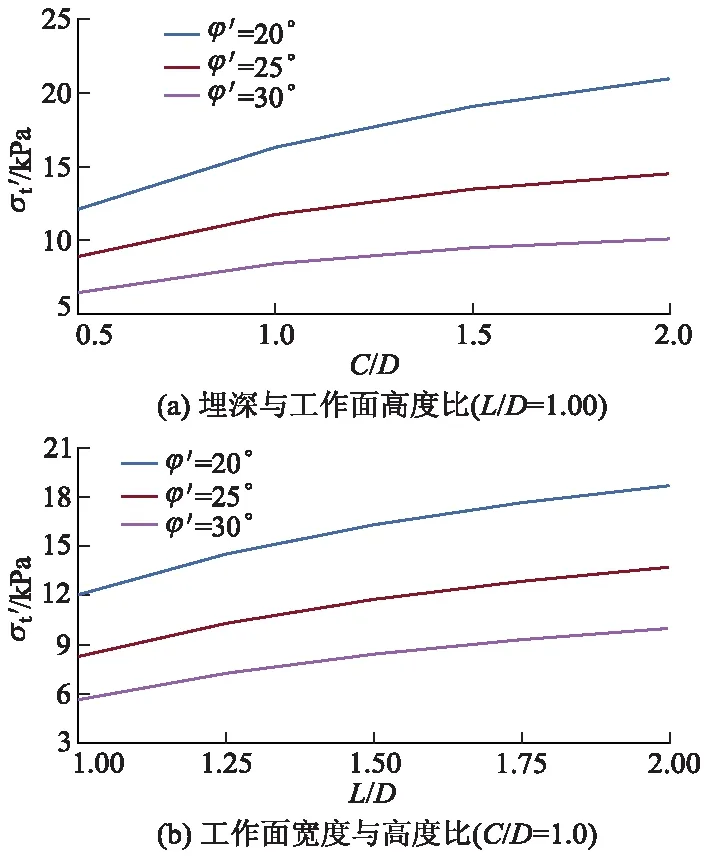
图12 c′=4 kPa时，极限支护压力与几何参数关系曲线

图12b中，随着工作面宽度与高度比值的增加，极限支护压力呈非线性增加趋势，变化规律与C/D类似，原因在于工作面宽度的增加导致了土拱效应减弱，隧道上覆土压力增大，使得工作面所需支护压力增加.

4.3 不同模型的支护压力对比

本节主要对比传统模型、优化模型的解在几何模式上的区别，并对依托工程中矩形顶管掘进面支护压力进行对比验证，结合沉降监测数据，验证本文计算模型在实际工程中的适用性.传统模型和优化模型的破坏模式特征参数(θ和α)随几何参数变化情况对比结果如表6所示.

表6 传统模型和优化模型的破坏模式特征参数随几何参数变化情况对比

由表6可知：两模型θ值相近，笔者提出的模型优化了α值，使得模型破坏情况更符合实际；随着埋深增大，优化模型α值增大，与传统模型趋于接近；随着工作面宽度增大，优化模型α值减小，逐渐偏离传统模型，这是由于考虑了土拱效应，此时优化模型的优势更为明显.

以表6中L/D=2.00，c′=4 kPa，C/D=1.0，φ′=30°，D=6 m，传统模型α=90.0°，优化模型α=78.9°为例，对两个模型体积进行对比.两模型体积对比示意图见图13，其中红线模型为优化模型.

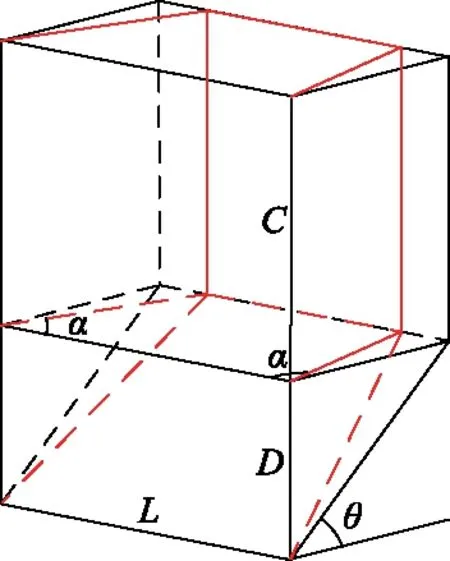
图13 传统模型和优化模型体积对比示意图

依据工程实际参数，其中土体参数按土层厚度作加权处理，通过优化模型和传统筒仓模型计算，得到极限支护压力(有效应力加上静水压力)和监测开仓清障施工阶段的监测土压力.传统模型和优化模型的极限支护压力理论计算值分别为49.03和51.36 kPa，开仓清障施工现场的支护压力监测值为71.00～90.00 kPa.通过对优化模型与传统模型结果进行对比，发现优化模型得到的极限支护压力值大于传统模型，且在主动破坏模式下偏保守，更有利于保障实际工程安全.

依据笔者提出的理论优化模型，如果实际工程中的支护压力大于极限支护压力的理论计算结果，则说明仓内支护压力合适，之所以产生地表塌陷或较大的沉降，推测可能是因施工故障或不利地层条件引起工作面支护压力不足造成的.掘进过程中土仓压力较为稳定，在洞门加固区内掘进时压力有所增大，在第28环施工停机开仓清障时支护压力明显减小，并且随开仓时间增加而逐渐减小.

5 结 论

以苏州市轨道交通5号线某车站附属地下工程为研究背景，通过对传统楔形体模型进行改进，结合工程实测数据，对优化后的修正模型进行对比验证，研究浅埋大断面矩形顶管掘进面的稳定性.

1)推导出优化模型的支护压力公式，并对其进行最优化研究.计算出各设定条件下破坏模式参数(θ、α)的最优值，得到最优破坏模式.进行参数敏感性分析，得到支护压力的变化规律，支护压力随土体抗剪强度参数的增大而减小，随隧道几何参数的增大而增大.

2)对比传统筒仓模型和优化模型可知，通过优化模型得到的支护压力值大于传统筒仓模型.实际工程中以优化模型解为参考，有利于规避施工风险.

3)依据笔者提出的理论优化模型，实际工程中支护压力大于极限支护压力理论值，说明仓内支护压力合适，则发生沉降的主要原因是由开仓清障造成的支护压力不足引起的.