基于混合精度ADC量化的大规模MIMO系统能效联合优化算法
曹海燕,汪忠亮,徐好,陈千鸿,许方敏
(杭州电子科技大学,浙江 杭州 310018)
0 引言
随着现代通信技术的发展,电子设备对网络容量以及数据吞吐率的需求日益提高。利用大规模多输入多输出(multiple input multiple output,MIMO)技术可以很好地满足要求,并且MIMO技术可以极大地提高系统的频效(即频谱效率),同时,降低功耗以提高能效(即能量效率)[1-3]。在大规模 MIMO系统接收端,每根射频链上都会部署模数转换器(analog-todigital converter,ADC)将所接收的模拟信号转变成数字信号,再交由基带处理。其中,ADC的功率损耗会随着量化精度的提高以指数级增加,因此,怎样在保持ADC较高精度的情况下尽可能减小功率损失成为近年来的研究热点之一[4]。文献[5]分析了在ADC量化比特数均为1 bit时的系统性能,文献[6]在ADC全为低分辨率的情况下阐明低精度 ADC造成的性能损耗可以通过增加接收天线的数量来补偿。文献[7]同样也是在 ADC全为低分辨率的情况下联合量化精度、导频长度和用户发射功率来优化能效。以上文献都是在ADC全部为低分辨率的情况下进行能效分析的。但在现实应用场景中,采用全低分辨率ADC会导致系统性能的损失,并且低精度ADC会导致接收端进行信道估计时出现信道失真的风险,因此学术界提出了混合精度ADC的系统架构[8]。其中一部分天线采用高分辨率ADC,以此可以在信道估计时获得更加准确的信道状态信息(channel state information,CSI),剩余天线装配低分辨率ADC来降低系统的功耗和硬件成本。文献[9]研究了在混合精度ADC架构下,采用MRC检测算法分析了大规模MIMO系统的频效。由于文献的优化目标为频效,所得结论忽略了基站端天线数以及量化精度对于能效所产生的巨大影响,不具备应用可行性。文献[10]分析了单小区大规模 MIMO系统采用混合精度 ADC架构时低精度ADC的量化位数对于系统能效和频效的影响,其中发射功率以常数代替。文献[11]针对中继系统中同时采用具有混合精度ADC和DAC的大规模MIMO系统架构,在固定发射功率的情况下分析了低精度 ADC的量化比特数对系统能效和频效的影响。文献[10]和文献[11]均在固定功率的情况下分析量化精度对系统性能的影响,而未经过优化的发射功率会导致能效和频效的结果很差。文献[12]在文献[11]的基础上研究了以系统频效为目标的发射功率优化问题,同时观察量化精度对于系统能效的影响,而忽略了基站端天线数对系统能效的影响。
基于以上分析,本文联合考虑用户发射功率、基站端天线数和低分辨率ADC量化比特数三变量的资源分配对系统能效进行优化。考虑在混合精度 ADC架构中基站端配备高精度ADC的天线数目对系统性能会产生巨大的影响,本文首先在给定基站端配备高精度ADC天线占比率z的情况下,通过在基站接收端采用MRC检测算法接收用户的发射信号,基于加性噪声量化模型[13](additive noise quantization model,ANQM)推导出具有混合精度 ADC的单小区大规模MIMO系统上行链路的可达速率和系统功耗的近似闭式表达式。以发射功率和用户服务质量为约束条件建立能效优化模型,再将分数形式的能效表达式通过分式规划方式转变为减式,利用拉格朗日算法和梯度下降法对低精度ADC量化比特数、用户发射功率以及基站端天线数进行联合优化得出最佳能效值,并在此优化算法基础上分析占比率z对系统性能的影响。
1 系统模型
本文考虑的是单小区大规模MIMO系统的上行链路。基站(base station,BS)端配备了M根天线,每根天线由单个射频链驱动,服务于小区内的K个用户,每个用户设备均为单天线。其中,有M0根天线连接高分辨率ADC,M1=M−M0根射频链连接了低分辨率ADC。其中,M0=z×M,z为高精度ADC在混合 ADC架构中的占比率。基于混合 ADC精度架构的大规模 MIMO上行链路系统模型如图1所示。
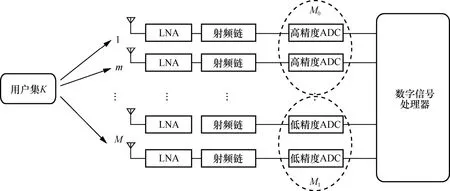
图1 基于混合ADC精度架构的大规模MIMO上行链路系统模型
假设基站具有完美的CSI并服务于均匀分布在小区内各个位置的用户,并且所有用户共享同一时频资源块。则BS接收的信号表示为:

其中,p为K个用户的发射信号功率矩阵,p=diag {p1,p2, …,pk}。G=HD1/2代表基站和用户之间的信道矩阵,H为M×K维的快衰落系数矩阵,D=diag{β1,β2, …,βk}表示大尺度衰落矩阵。n为M×1维加性白高斯噪声,满足n~ CN(0,I)。x作为K×1用户发射数据满足E{ |xk|2} = 1。由于该系统采用的是混合精度ADC的系统架构,则,定义G0表示为用户与M0根配备高精度ADC的天线之间的信道矩阵。同理,G1表示为用户与M1根配备低精度ADC的天线之间的信道矩阵。可以得到:
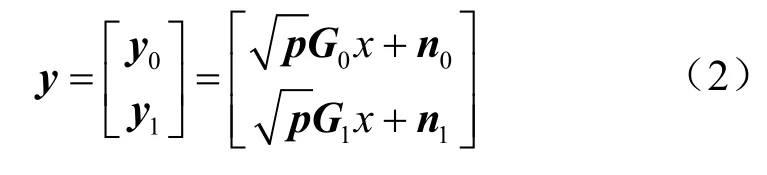
本文采用AQNM模型对量化过程进行分析。由于低精度量化存在量化误差,假设输入信号为y,则输出信号yq=αy+nq。α=1−ρ,ρ为量化信噪比的倒数,大小取决于量化比特数b,当b=1~5 bit时,ρ的参考值见表1。当b大于5 bit时,
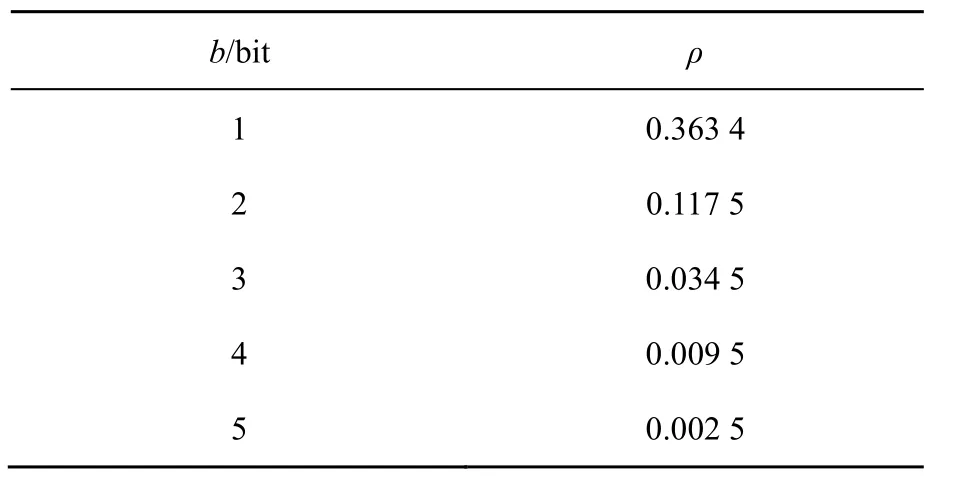
表1 不同量化精度对应的ρ值
nq为系统的加性量化噪声,其协方差函数可表示为[11]:
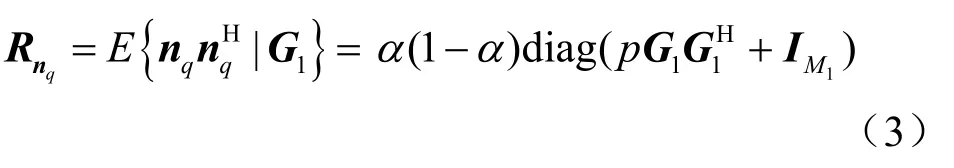
考虑所有低分辨率ADC的量化比特数相同,并假设高分辨率ADC可实现完美量化,则量化后的信号可表示为:
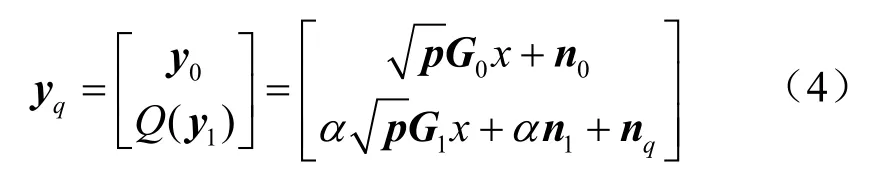
1.1 系统性能分析
本节将使用 MRC接收算法推导出上行链路可达速率的近似闭式表达式。则根据式(4),可以推导得到检测后的信号向量:
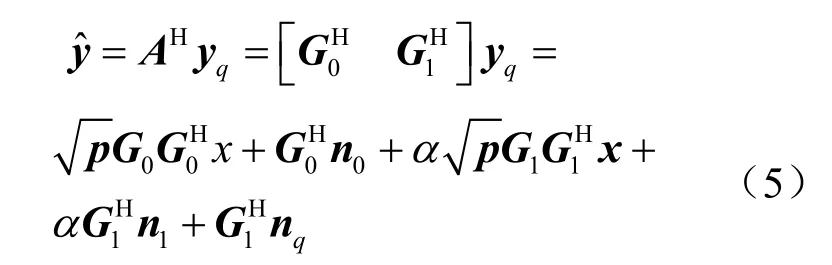
将式(5)展开,即可得到基站收到的第k个用户的信号:

其中,gH,i为第i个用户到配备高分辨率ADC天线的信道,gL,i为第i个用户到配备低分辨率ADC天线的信道,pi为第i个用户信号传输功率。根据香农公式,得到kth用户的可达速率为:
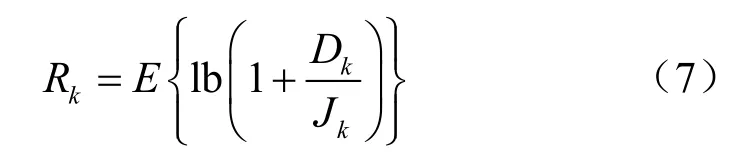
根据詹森不等式可得到Rk的下界:
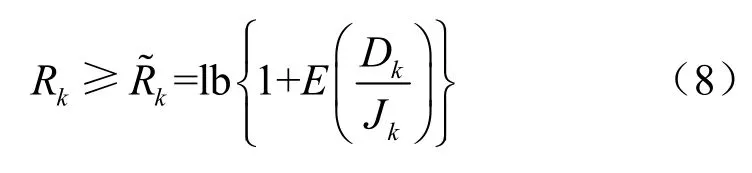
其中,Dk为期望信号功率,化简可得[14]:
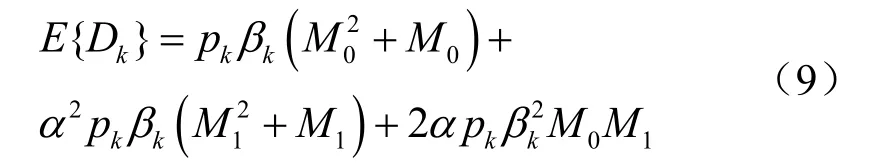
根据伽马分布可对量化噪声进行计算并化简[15]:
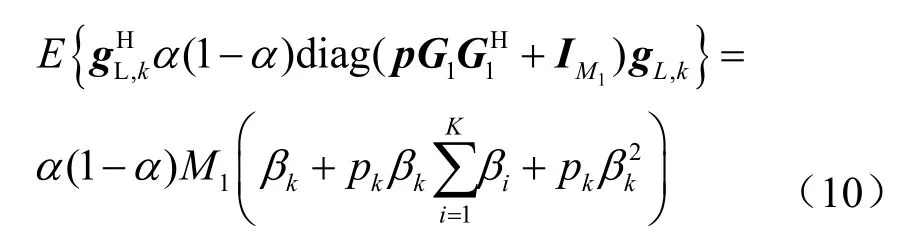
其中,Jk为干扰信号功率与噪声功率[15]。
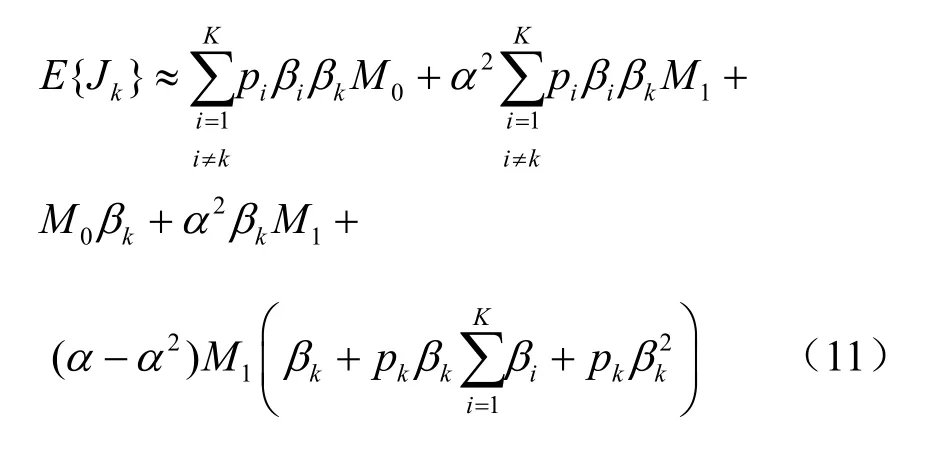
考虑一般用户上行信号的信干噪比(signal to interference and noise ratio,SINR)≫1,可将式(11)化简为:
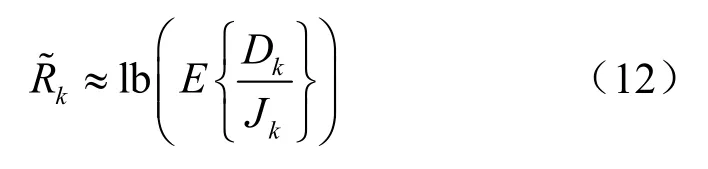
1.2 系统功耗模型
本节将介绍大规模MIMO系统的功率消耗,其主要由3个部分组成。
(1)接收端功率放大器功耗PPA的计算式为:
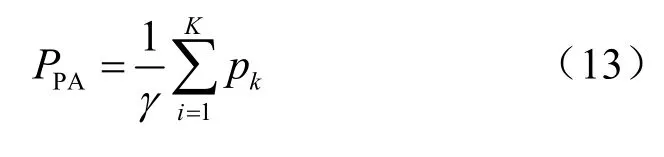
其中,γ∈ [ 0 , 1],表示功率放大器的放大效率。
(2)收发器功耗PTR的计算式为:

其中,PUE表示用户设备的功率损耗。PBS表示每根天线中电子元器件的功率损耗,主要包括模数转换器(ADC)的功率损耗PADC、自动增益控制功率损耗PAGC、低噪声放大器功率损耗PLAN以及滤波器等其他电子器件的损耗。其中,PADC=FOMWfs2b。b为量化比特数,fs为奈奎斯特采样速率, F OMW为品质因数[16],用于评价ADC的功率效率,在1 GHz带宽时能量损耗一般为5~15 fJ/conversion step(表示ADC每一次转换的步骤大约消耗5~15 fJ的能量)。用于表示其他损耗功率。收发器链路的具体功耗可具体表示为:
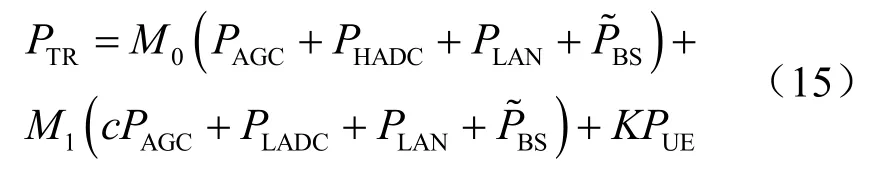
(3)基站端进行信号处理、信道编解码等线性处理过程产生的功率损耗PLP以及其他未计算的特定功耗Psite的计算式为:
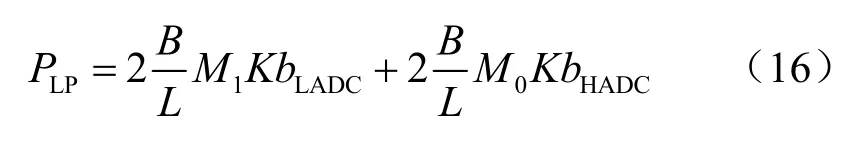
其中,B为系统传输带宽,L为基站的运算效率,假设高精度ADC可以实现信号的完美量化,则理论上bHADC应趋于无穷大。
依据式(13)~式(16),可得出系统最终消耗的总功率Ptotal:
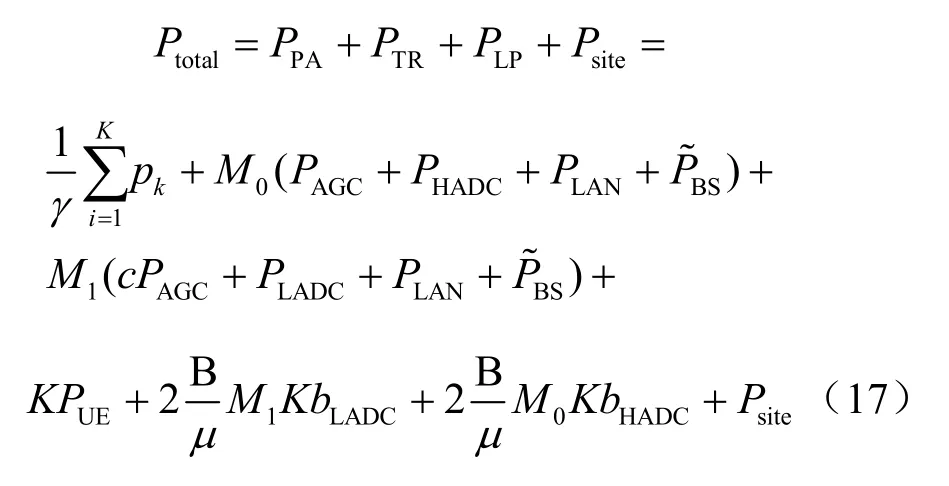
其中,c的数值与量化精度相关,表示为:

2 能效优化算法
本节将具体描述配备混合精度 ADC的大规模MIMO系统的能效优化算法,依据该算法优化低分辨率ADC的量化比特数、用户的最佳发射功率以及基站端天线数,以此得到系统的最佳能效值。
2.1 问题描述
通信系统的能效(energy efficiency,EE)可以定义为:
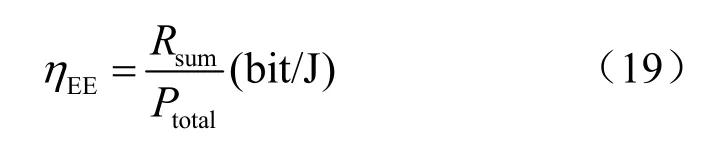
依据式(12)、式(18)和式(19),同时考虑实际系统运行中所需的最低数据传输速率和单用户的最高发射功率,可以建立以系统能效最大化为目标的目标函数:
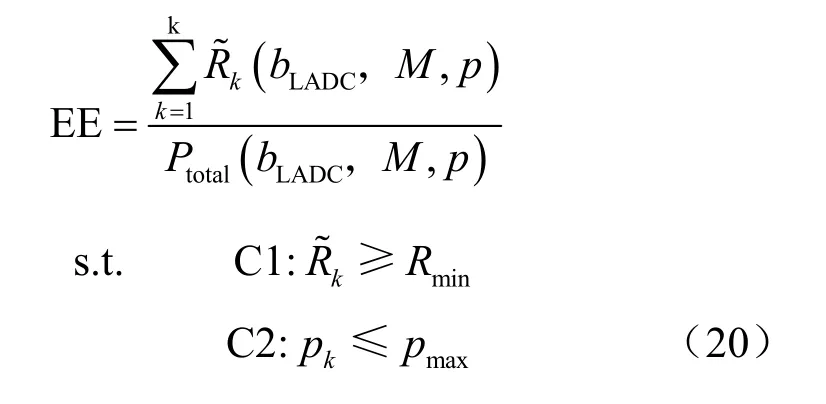
2.2 问题转化
从式(20)可以看出,这是一个具有三变量(bLADC,M,pk)的复杂非线性函数,并且含有两个线性约束条件,为了解决这个含有约束条件的非凸优化问题,需要对目标函数进行简化处理以方便计算。
首先,先对进行处理,根据对数函数计算规则,可知:
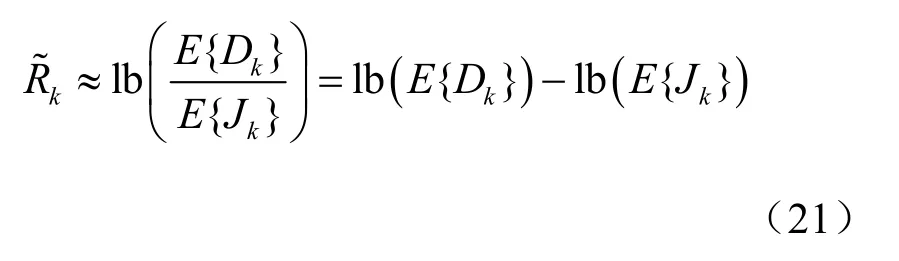
其次,利用分数规划将式(20)的分数形式化为等价的减式形式,目标函数转变为:
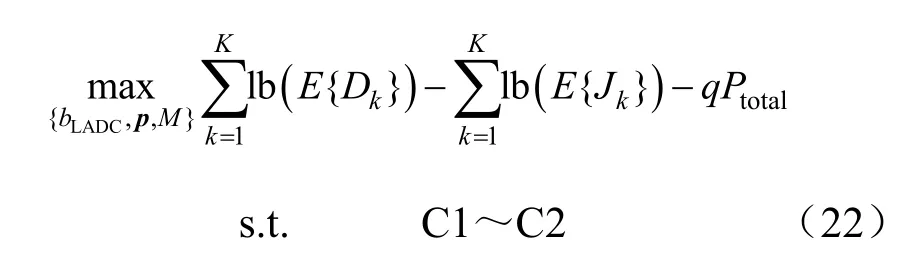
其中,q为表示能效值的辅助变量。
从式(22)中可以证明这是一个关于变量M和p的联合凸函数,因此可以采用凸优化理论来进行求解。由于这是一个具有三变量的目标函数,为了简化计算,首先应初始化量化精度bLADC,在此基础上再对p和M进行优化,之后利用迭代的方式确定最优的量化精度。
对于确定bLADC之后,采用拉格朗日方法消去约束条件,即:
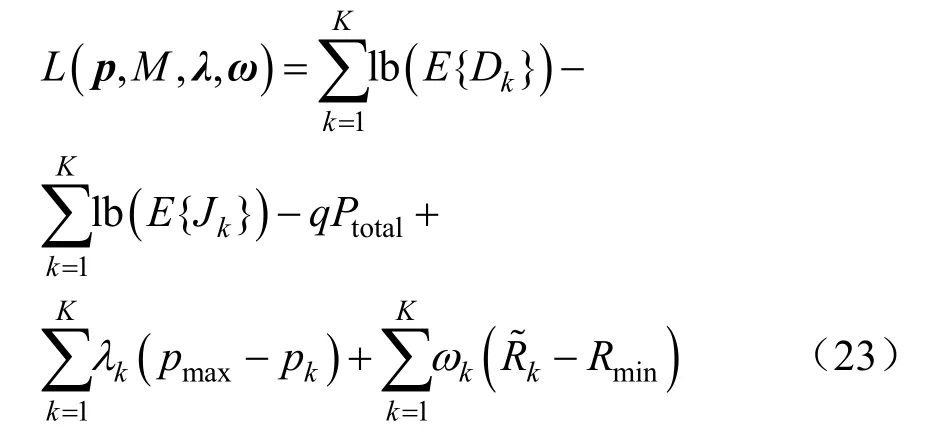
其中,λ= (λ1,λ2,… ,λK),ω= (ω1,ω2,… ,ωK),且λk≥0、ωk≥0分别表示约束传输速率和发射功率的拉格朗日乘子。
2.3 问题求解与算法优化
对于式(23)给定的优化问题,首先采用KKT条件,对pk进行求导,即令:,可得此时的最优发射功率:
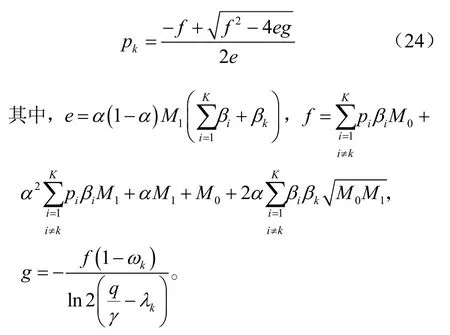
关于天线数M的优化,在此系统模型中,考虑利用,难以求得天线数M的具体表达式,也就无法再利用拉格朗日算法求得,但可以将M看作一个难以求导的参量,且,于是可以利用梯度下降法对天线数M进行优化,具体的计算式为:
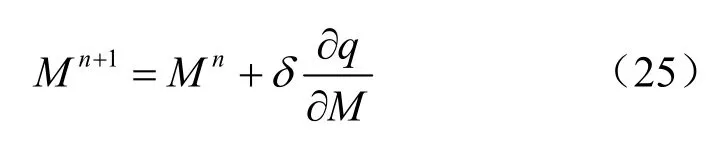
其中,δ为学习率,决定了天线数M的变化快慢,■■为向上取整符号,n为迭代次数。然而实际情况是,梯度下降法适用于无约束的情况。所以需要判断在优化pk后,每次所取的M值是否满足C1,但是可以观察到Dk中存在M的二次方,Jk中只存在M的一次方。由于该系统是一个大规模MIMO系统,天线数一般为上百根。所以在正常情况下,Dk的值是远大于Jk的,并且在之后对天线数量的仿真调试中,可以得到本文的仿真结果均满足C1,这也验证了天线数M的优化是可以利用梯度下降法来解决的。
依据式(23)~式(25)的计算分析,本文基于 Dinkelbach[17]方法提出了一种能效优化方案,通过不断地对能效值q进行迭代使之最终收敛在一个阈值内。具体算法步骤如下,其中,Δλ和Δω为拉格朗日算子的迭代步长,τ为终止循环的阈值,[x]+= m ax{0 ,x}。

3 仿真与分析
本节所给出的仿真结果将验证所提算法在能效优化方面地优越性以及其计算结果的准确性。假设信道具有完美的CSI,并且小区内部用户均匀地分布在基站周边。部分仿真参数见表2。
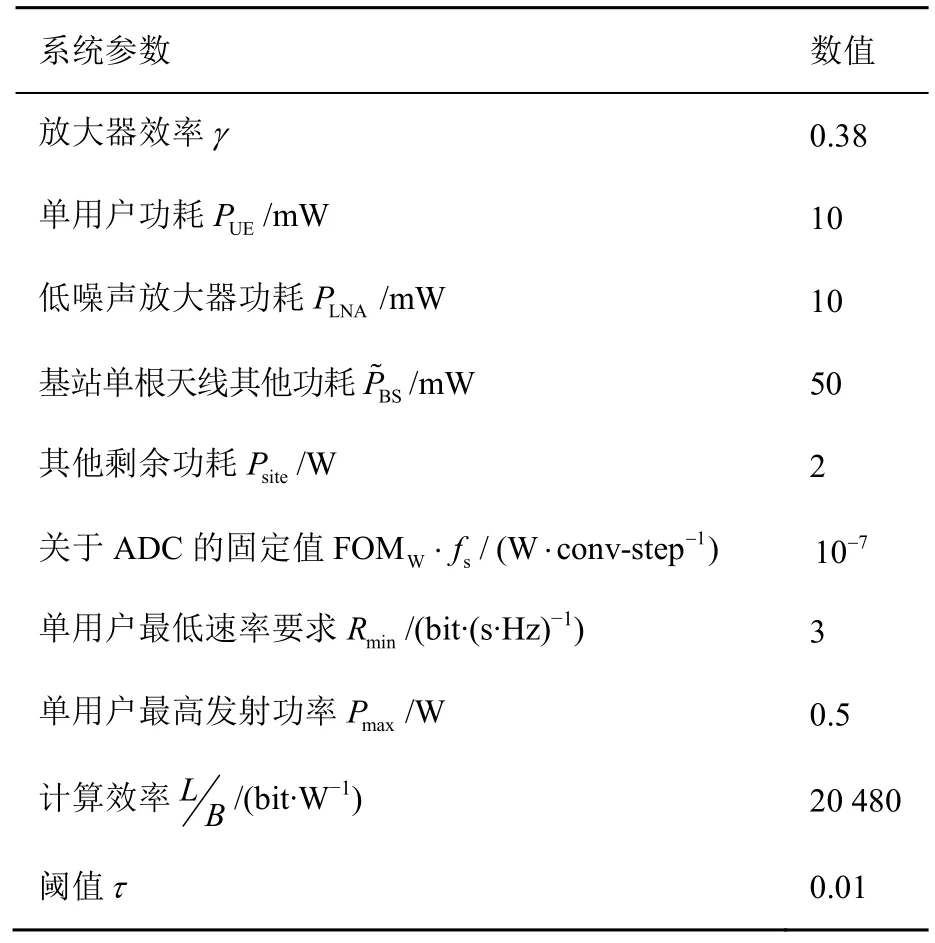
表2 部分仿真参数
不同量化比特数对能效的影响如图2所示。对3种情况进行了仿真:高分辨率ADC天线占比率z=0、高分辨率ADC天线占比率z=0.25以及高分辨率ADC天线占比率z=0.5。从图2可以看出,随着配备高精度 ADC天线占比的增加,能效反而下降,这是因为高精度 ADC意味着需要更高的能耗才能达到完美量化。不同量化比特数与占比率z对能效的影响如图3所示。
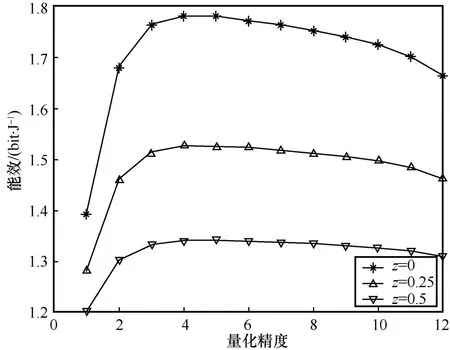
图2 不同量化比特数对能效的影响
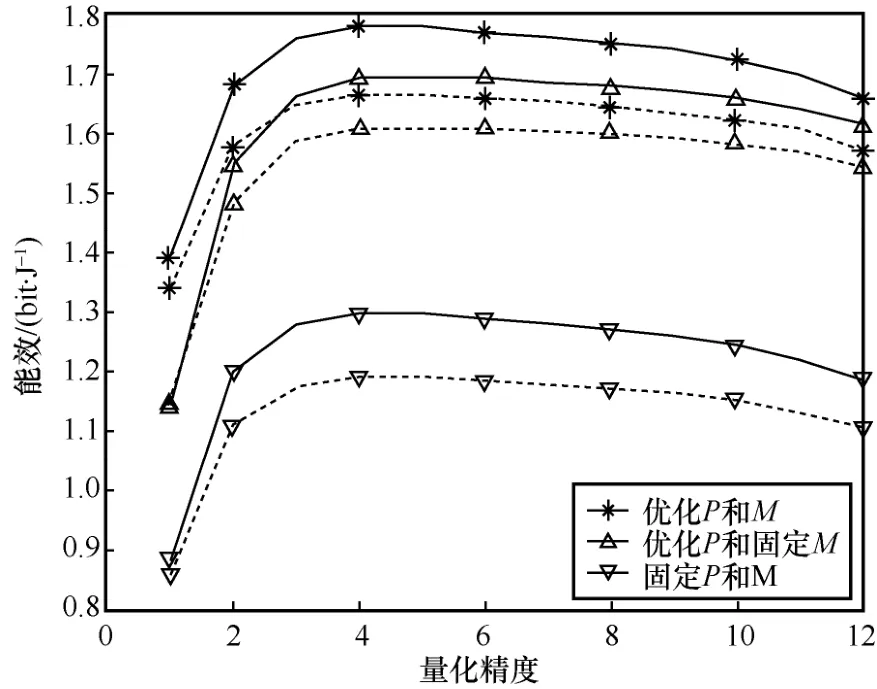
图3 不同量化比特数与占比率z对能效的影响
在图3中,由于同时优化了用户的发射功率和基站端天线数,尽管基站端配备了高精度ADC,其能效仍比文献[18]中所采用等功率分配的纯低分辨率ADC天线系统要高,其中虚线代表z=0.1时的能效仿真,实线代表z=0的能效仿真。
不同量化比特数对频效的影响如图4所示,分别对3种情况进行了仿真:高分辨率ADC天线占比率z=0、高分辨率ADC天线占比率z=0.25以及高分辨率ADC天线占比率z=0.5。仿真表明,虽然纯低精度 ADC的能效性能较之混合精度量化的系统架构更好,但后者可以带来更高的频效。此外,混合精度量化结构中的高精度 ADC可以在信道估计时降低信号失真的风险,获得更完善的CSI。综上所述,混合精度量化的系统架构可以在损失一部分能效为代价的情况下获得更好的频效。
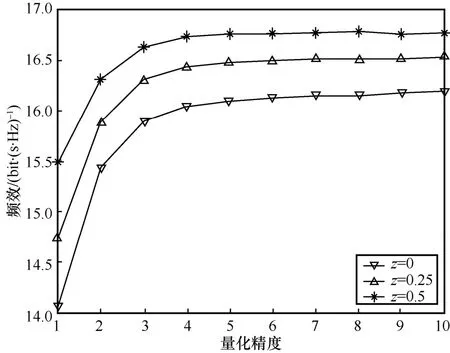
图4 不同量化比特数对频效的影响
不同用户数对能效、频效的影响分别如图5、图6所示。可以发现,使能效最优的比特数大约为5 bit。能效值会随着用户数的增多呈现先上升后下降的趋势,这是因为系统的可达速率会随着用户数的增加而提高,但同时用户端的功耗也会随之逐渐增加,且变化量会逐渐大于同比增加的可达速率。同时由于 SE=R/B(bit·(s·Hz)-1),在固定量化比特数的情况下所以频效会随着用户的增加而不断提高。图6中,b=5和b=10时的SE相同是因为随着量化精度的提高,对应的α值会趋向于1,使得其SE不再提高。从图5和图6可以看出,优化后的EE和SE值远高于文献[10]所提的等功率分配。
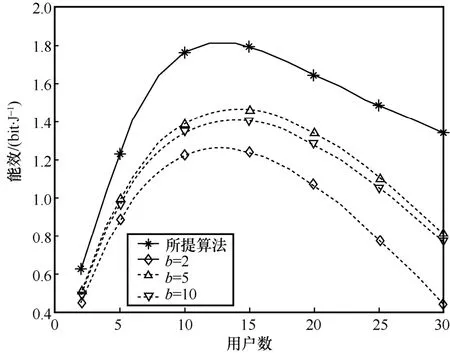
图5 不同用户数对能效的影响
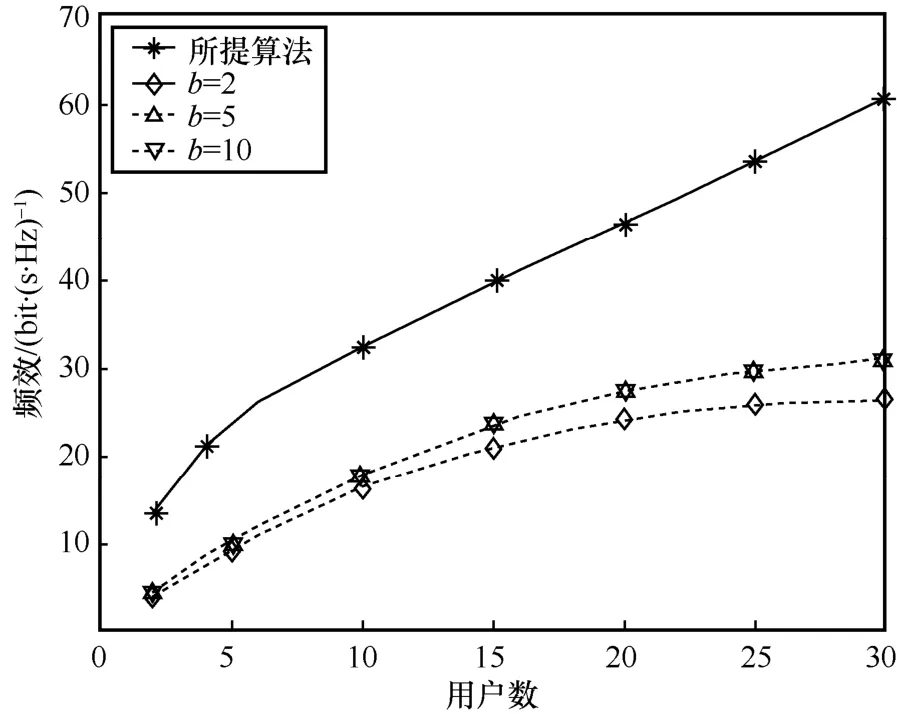
图6 不同用户数对频效的影响
量化比特数对频效和能效的影响如图7所示。从图7可以更直观地看出占比率z可以作为一个自适应的参量,通过调整z的值来权衡系统能效和频效的值。分别对以下3种情况进行仿真:高分辨率ADC天线占比率z=0、高分辨率ADC天线占比率z=0.25以及高分辨率ADC天线占比率z= 0.5。从图7可以看出,在不同情况下,当量化比特数为5 bit左右时,此时系统性能均可以大致达到最优状态,即最优的能效以及相对较高的频效。
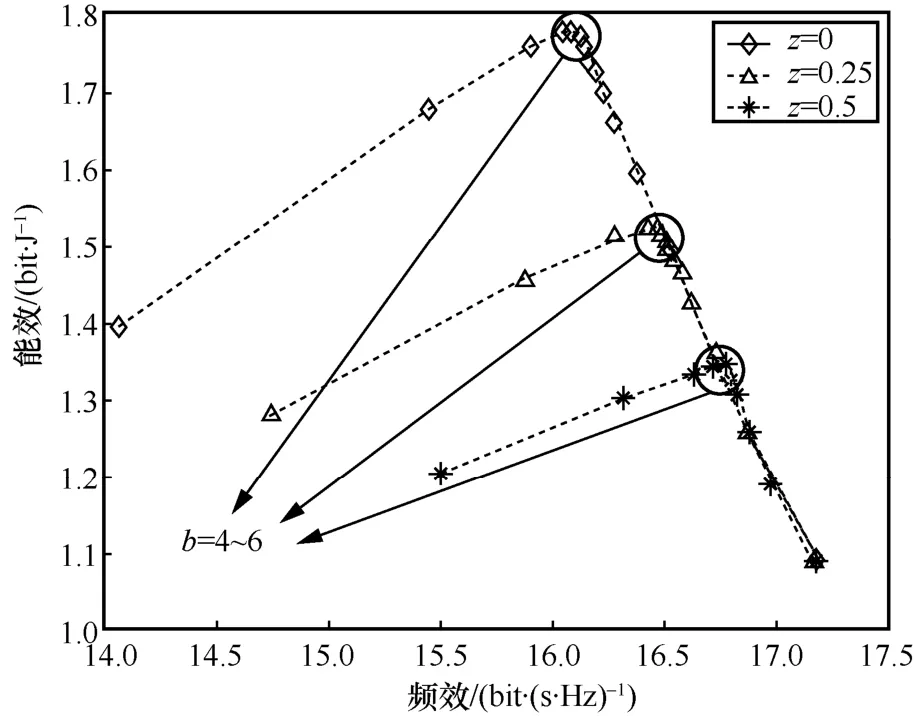
图7 量化比特数对频效和能效的影响
系统频效与接收机功耗的关系如图8所示,可以看出混合精度ADC架构的接收端功耗要高于低精度ADC架构。但是经过优化后,在相同的能量消耗情况下,频效得到很大的提高,且在较低量化位数的情况下,例如在1~3 bit时,系统频效增加较为显著,而接收机的功耗增加量几乎可以忽略不计。利用优化算法后,能量消耗甚至出现了下降,这是因为优化了天线数,使得资源分配更合理,使其达到更少的功耗。随着继续提高低分辨率量化器的量化比特数,系统的功耗会有明显的提高且频效几乎不再增加。这表明,适当选择低分辨率ADC的量化比特数(约为5 bit),使得系统可以在频效和功耗之间得到更好的折中。
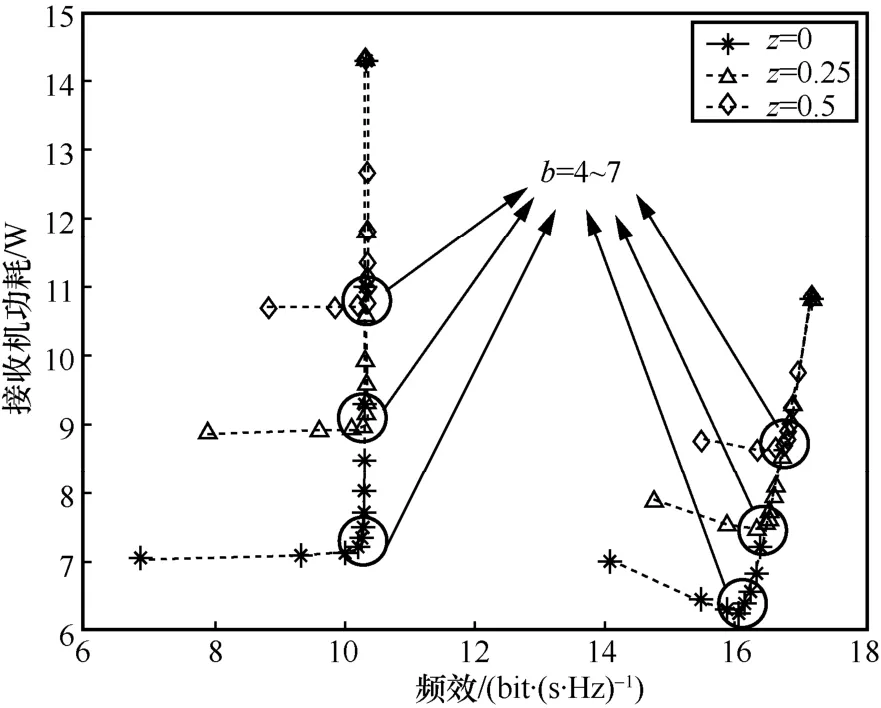
图8 系统频效与接收机功耗的关系
4 结束语
针对配备混合量化精度 ADC的大规模MIMO系统所带来的功耗过大的问题,本文提出了联合用户发射功率、低分辨率ADC量化比特数和基站端天线数进行优化的算法。采用交替迭代的优化方式得到最优的能效值。仿真结果验证了该优化算法对于能效和频效均有一定程度的优化。进一步分析了配备高分辨率ADC的天线占比率z对系统能效和频效的影响,发现z可以看作一个自适应的参量,通过改变z的大小对能效和频效在系统中所占的权重进行动态调整,以满足不同工作场景的需求。后续的研究将进一步考虑在未知信道状态信息的情况下能效的优化情况。

