基于动态安全域的静态电网输电线路安全概率自动评估方法

陈莉波，白困利，周统刚，秦煜森

（国网重庆市电力公司，重庆 404100）

0 引言

输电线路的运行效率直接决定了静态电网的工作质量。现代静态电网复杂庞大，设备容量和电网容量的不断增大导致电网电压等级不断升高，为了追求更大的规模效益，以区域电网互联为目的的高压输电技术逐步应用到静态电网中[1]。采用高压传输技术可以改善电力系统的运行效率，但也会使电力系统的不确定性增大。受到天气、人为破坏以及线路设备等因素的影响，输电线路会存在较大的运行安全问题，为此有必要设计并应用输电线路的安全概率自动评估方法。

安全概率评估主要指的是针对目标运行过程中可能存在的危险性以及可能产生的后果进行综合评价的分析方法，输电线路安全概率的评估结果对于线路的维修与管理工作具有较高的参考意义。从输电线路安全概率评估方法的研究现状来看，基于AADL的安全评估方法以及基于电压相量时序轨迹特征的安全评估方法应用范围较广，然而在实际应用过程中，上述现有的评估方法存在明显的评估效果不佳、应用价值低等问题，为此提出了动态安全域的概念。

安全域是指在给定的网络结构和特定的事件情况下，在注入空间中定义了满足各种安全稳定条件的操作点。在概率安全分析的概念中，安全被视为系统的工作状态，与将要到来的干扰有关。在系统出现故障时，系统处于暂态稳定状态，此时称之为“动态安全域”。将动态安全域应用到静态电网输电线路安全概率自动评估方法的优化设计工作中，提高输电线路安全概率评价的可行性。

1 静态电网输电线路安全概率自动评估方法设计

在传统输电线路安全概率自动评估方法的基础上，应用动态安全域的概念，在静态电网环境中对评估方法进行优化。优化的输电线路安全概率评估流程，如图1所示。

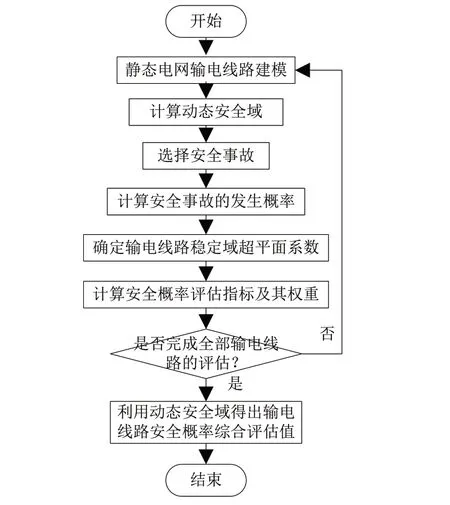
图1 静态电网输电线路安全概率自动评估流程图

按照上述流程首先确定评价目标，对影响输电线路安全状态的参量进行分析，并确定评估指标，对其进行量化处理，得出综合评分和安全概率等级，以此作为评估方法的最终输出结果。

1.1 构建静态电网输电线路数学模型

从结构上来看，静态电网输电线路由线路杆塔、导线、绝缘子、拉线、接地装置等元件构成，输电线路的工作参数包括长度电阻、电感、电容和电导[2]。其中导体自电位系数与互电位系数可以表示为：

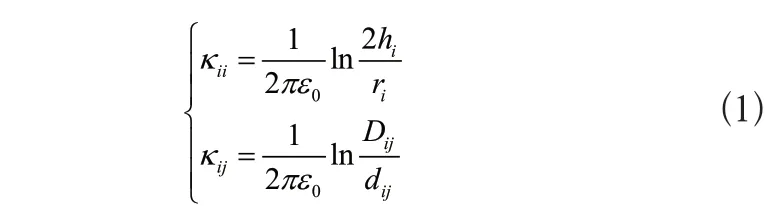
式(1)中hi和ri分别为输电线路导线i对地的平均高度和半径，Dij和dij对应的是导线i与j之间的镜像距离和实际距离，变量ε0为输电线路所处环境中的空气介电常数，Kii和Kij分别为导线i的自电位系数及其与导线j之间的互电位系数。输电线路单位长度阻抗的计算公式如下：

式(2)中Rii表示交流电阻值，hi为对地高度值，表示的是几何平均半径，ΔX对应的是大地影响修正项，最终的计算结果即为导线i的自阻抗及其与导线j之间的互电阻。按照上述方式可以得出静态电网输电线路中的其他工作参数，将其导入到输电线路的结构模型当中，最终得出静态电网输电线路数学模型的构建结果。

1.2 自动采集输电线路实时运行数据

以构建的输电线路模型为基础，采集线路的实时运行数据，具体包括电压、电流、负荷、潮流等。以电压数据为例，该类型数据的自动采集结果可以表示为：

其中U0和Ut分别表示输电线路的初始电压和t时刻电压采集结果，θi表示节点i电压的相角。在构建的线路模型上设置测点，按照上述方式可以得出输电线路在任意时刻的运行数据采集结果。

1.3 计算静态电网输电线路动态安全域

静态电网输电线路在经历一个大扰动后，通过继电保护、自动重合闸等装置切除故障后，切除故障，假设故障持续的时间为，可以把输电线路经历这个扰动的过程分为三部分，分别记为事故前线路Gfront、事故后线路Gafter和事故中线路Gaccident，上述三个阶段下的输电线路方程可以表示为：

式(4)中fGi为状态函数，x0、x1和x2分别为三个阶段的状态变量，y为扰动发生时的注入总量，τ为事故清除时间[3]。则节点注入空间上静态电网输电线路动态安全域可以量化表示为：

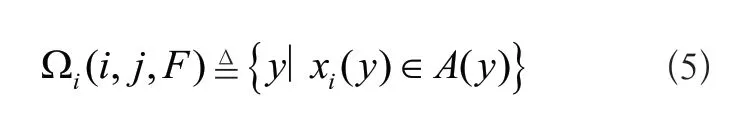
其中F为既定事故，通过公式(4)的计算可以得出变量xi(y)的具体取值，A(y)为由注入功率所决定的平衡点的稳定域。图2表示的是静态电网输电线路的动态安全域。

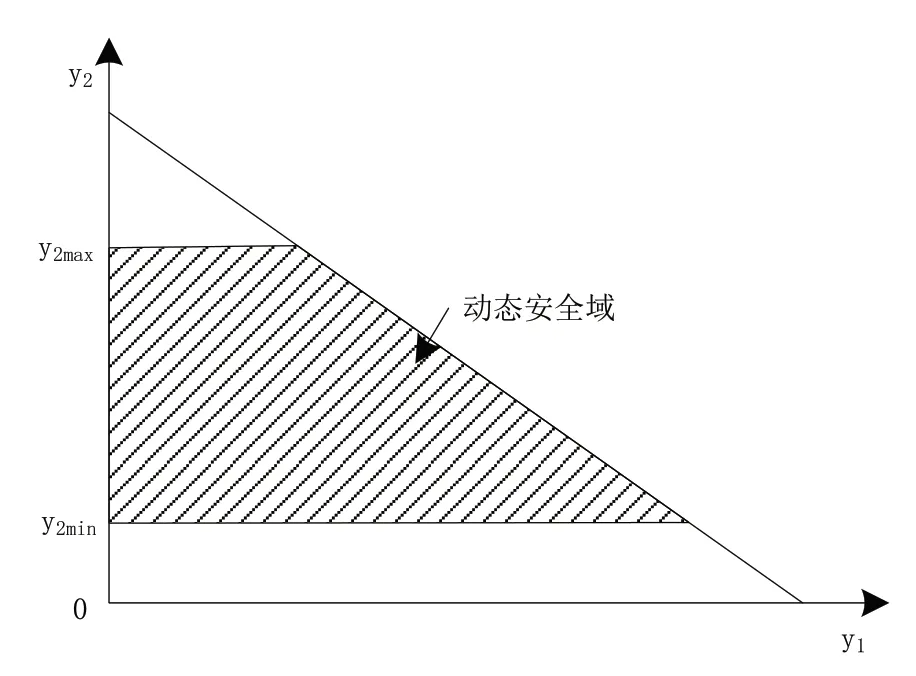
图2 静态电网输电线路动态安全域示意图

对于给定事故及注入功率，定义tcr为事故临界注入点，tcr满足以下条件：tcr时刻前输电线路保持暂态稳定，tcr时刻后输电线路处于失稳状态。在已知注入功率量的前提下，判断当前注入是否为临界注入点，若判断结果为正确，则该点即为临界注入功率点，否则调整注入功率量，重复上述搜索步骤，直到得出搜索结果为止[4]。用临界注入功率上下限的超平面来描述电力系统的动态性安全域，该临界超平面可表示为：

其中αi和βi分别为动态安全域超平面方程的系数，Pi和Qi对应的是注入功率空间上的临界注入向量。利用公式(6)表示的超平面进行拟合计算，得出静态电网输电线路动态安全域参数的计算结果。

1.4 选择并计算输电线路安全概率评估指标

静态电网输电线路在运行过程中会发生的安全事故包括电压越限、线路过载等类型，其中电压越限事故的发生与输电线路自身的运行状况有关，相关影响因素包括线路负荷、负荷分配等运行参数的变化，线路过载的影响因素包括线路的焦耳热量、线路辐射热量、线路对流热量等。根据输电线路安全影响因素的分析结果，在科学性、整体性原则的约束下，选择线路安全概率的量化评估指标，其中部分指标的选择情况如表1所示。

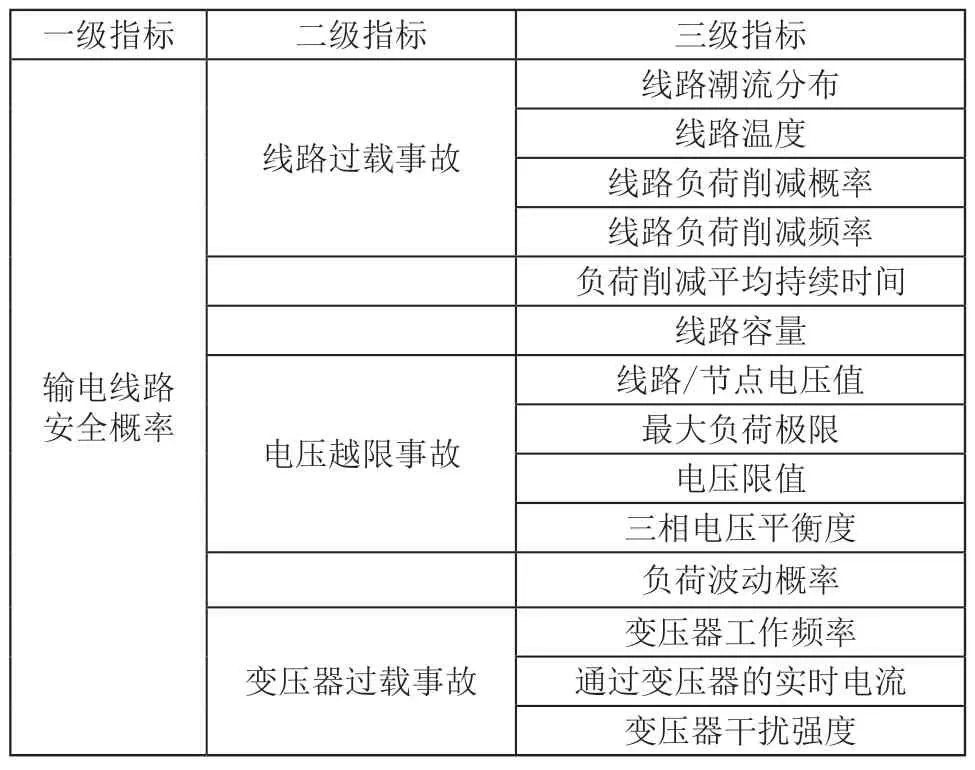
表1 输电线路安全概率评估指标说明表

表1中负荷削减概率指标的计算公式如式(7)所示：

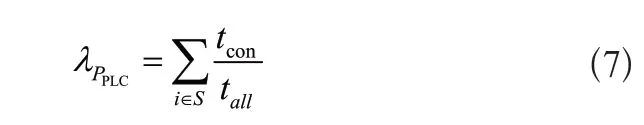
式(7)中tcon和tall分别为输电线路处于安全状态的持续时间以及运行总时间，参量S为线路负荷削减的状态集合。同理可以得出线路负荷削减频率、负荷削减平均持续时间以及线路容量指标的计算公式为：

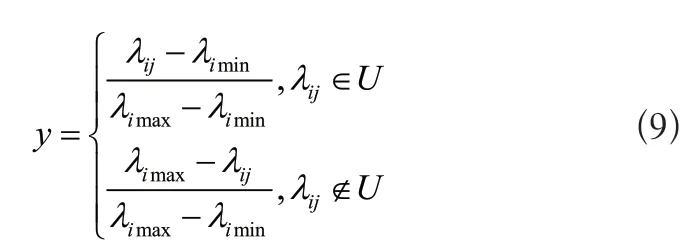
式(9)中λij为设置评估指标的实际取值，λimax和λimin为评价指标的最大值和最小值，而U对应的是正向指标集合。在此基础上，利用式(10)计算任意两个评估指标之间的相似度。

式(10)中m表示评估工作中设置的指标数量，λp和λq分别为第p和q个指标的量化值。若最终计算得出μi,j的值高于0.85，则判定p和q指标的相关性过高，需要剔除其中任意一个指标，降低指标之间相关性。

1.5 求解静态电网输电线路安全概率评估指标权重值

采用层次-熵组合法代替了传统权重计算法，用层次分析法求出了主客观权重，用熵权法求客观权重，把主客观权和客观权值相结合，再用最小二乘法优化了权值，通过多重组合逐层推理，得到了主客观相结合、自主优化的评价指标权值。层次分析法的基本思路是把多目标问题分解成多个目标，再用定性和模糊定量的方法求解多目标多方案优化问题[5]。熵权法的基本原则是对评价指标的信息熵进行计算，如果一个指标的信息较低，那么它所能提供的信息就会更多，从而使其在综合评价中的作用也会更大，所赋给的权重值就应该越大。利用层次分析法和熵权法得出的初始权重，分别记为ωj和φj，经过最小二乘法优化后得出的指标权重计算结果如式(11)所示：

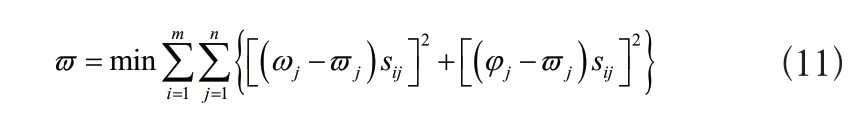
式(11)中sij为评价指标的无量纲化处理结果，m和n分别为层次分析法和熵权法计算得出的权值数量。通过对公式11的求解即可得到综合权重值。

1.6 实现静态电网输电线路安全概率自动评估

应用动态安全域计算输电线路中任意元件h发生故障时的动态不安全概率为：

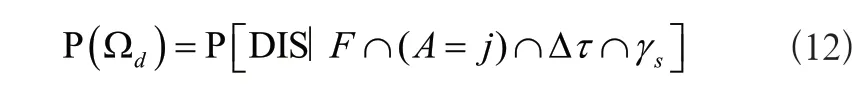
其中γs为故障发生地点离线路首端与线路总长度的比值，Δτ为故障持续时间。最终在动态安全域的支持下，静态电网输电线路安全概率的自动评估结果可以表示为：

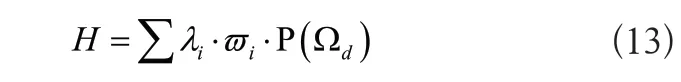
将评估指标的具体取值以及式11、式12的计算结果代入到式13中，得出输电线路安全概率评分，结合静态电网的安全使用规范，确定当前输电线路的安全等级。

2 性能测试实验分析

以测试基于动态安全域的输电线路安全概率自动评估方法的运行性能为目标，在某静态电网输电线路背景下，得出安全概率评估结果，并从评估精度性能和方法应用性能两个方面，判断优化设计方法是否达到预期设计效果。

2.1 配置静态电网输电线路环境

此次实验选择某市中心的静态电网作为研究背景，该电网包括交流输电线路和直流输电线路两个部分，其中交流输电线路的连接结构如图3所示。

图3 静态电网交流输电线路接线结构图

图3表示的输电线路中包含5个变压器设备，用来实现电压的转换，而选择的直流输电线路中的变压器安装数量为2个。交流输电线路和直流输电线路的长度分别为2.46km和4.85km，线路允许通过的最大电流值相同，均为6.0A，直流输电线路的电压等级为220kV，线路的弹性系数和抗拉强度分别为7000MPa和180MPa，单线分裂形式为单分裂，安装的绝缘子类型属于悬式绝缘子。为了保证静态电网的运行安全，此次选择的输电线路均为绝缘导线，在初始状态下检测各条输电线路的健康状况，保证选择的研究对象无故障现象。

2.2 描述性能测试实验过程

在实验开始之前，通过更换输电线路上的元件设备、加设干扰源以及人为破坏等方式，降低静态电网输电线路的安全等级，并计算出不同状态下线路安全概率的理论值，作为判断评估结果是否精准的标准数据。按照输电线路的地理位置，将其划分为6个组别，每个组别包含的线路数量不同，但线路长度相同。利用传感器设备收集不同工况下的输电线路运行数据作为实验的数据样本，将其代入到主测计算机中，通过安全概率自动评估方法的运行得出评估结果。图4为线路1-12的安全概率评估结果。

图4 静态电网输电线路安全概率评估结果

按照上述方式可以得出两种类型所有输电线路的安全概率评估结果。为了方便对优化设计方法评估性能的评估，设置安全概率评估误差作为评估精度性能的测试指标，其数值结果为：

其中Ptheory和Pass分别表示安全概率评估的理论值和实际输出结果。而优化设计评估方法的应用性能测试指标设置为：输电线路安全事故的发生频率faccident、安全事故持续时间Δtaccident以及事故带来的经济损失Mloss，在实际测试过程中指标Mloss可以通过数据记录与统计直接得出，指标faccident和Δtaccident的测试结果如下：

式(15)中naccident表示安全事故发生的次数，Ttest为测试时长，tend和thappen分别为输电线路安全事故的发生时间和结束时间。为保证基于动态安全域的静态电网输电线路安全概率自动评估方法的优化效果，要求安全概率评估误差不得高于0.5%，事故发生频率不得高于4次/月，事故持续时间和经济损失的最大预设值为0.5h和3.0万元。

2.3 性能测试结果分析

统计相关数据，通过式(14)的计算得出优化方法评估精度性能的测试结果，如图5所示。

图5 输电线路安全概率自动评估方法精度性能测试结果

从图5中可以直观的看出，优化设计方法在交流输电线路和直流输电线路中的概率评估误差分别为0.25%和0.14%，均低于0.5%。将优化设计的评估方法应用到输电线路的安全管理工作中，根据评估方法的输出结果进行线路维护，经过公式15的计算得出评估方法应用性能的测试结果，如表2所示。

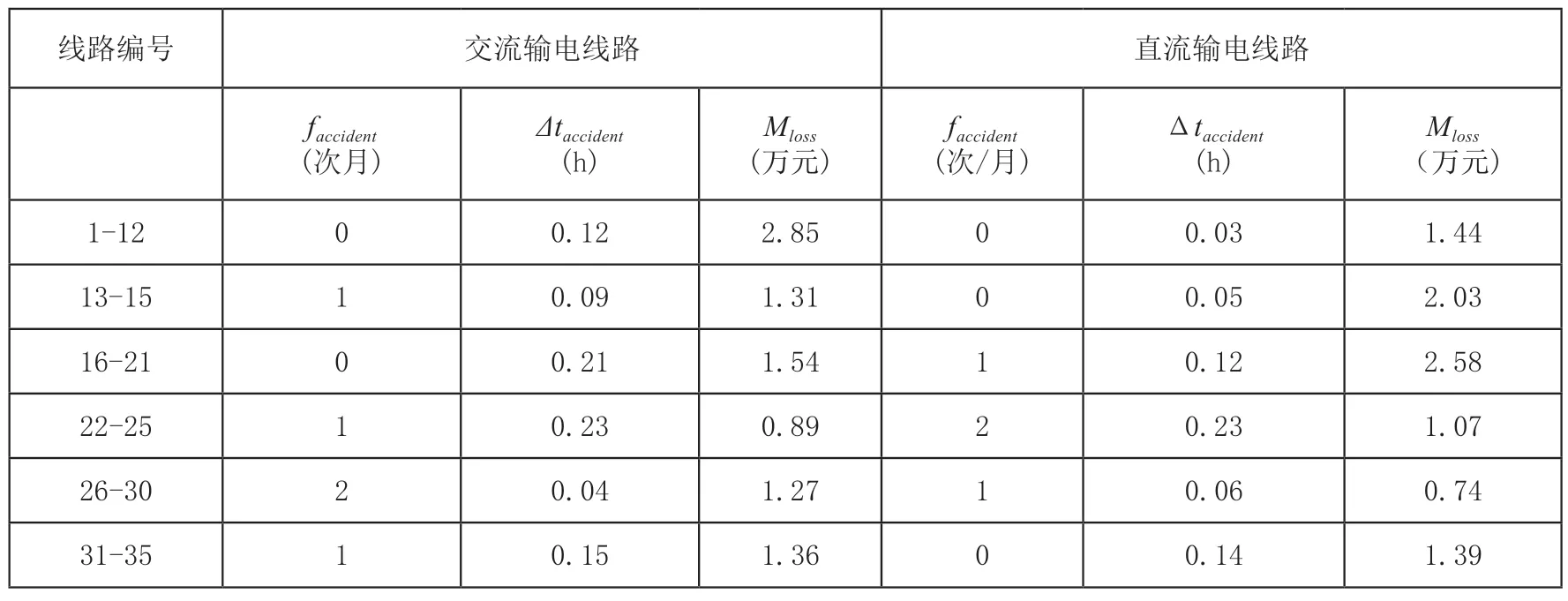
表2 输电线路安全概率评估方法应用性能测试结果

综合两种输电线路环境，可以得出应用评估方法后，输电线路安全事故发生频率的平均值为0.75次/月，平均事故持续时间和经济损失分别为0.123h和1.54万元，均满足预期要求。

3 结语

输电线路的安全性直接决定了静态电网的稳定性以及用户的用电质量，通过动态安全域理论的应用，给出较为精准的安全概率评估结果，参考评估结果可对输电线路的安全事故进行预防控制。