一种求解资源约束项目调度问题的改进引力搜索算法

刘永利，张晓阳

（河南理工大学 计算机科学与技术学院，河南 焦作 454000）

0 引 言

资源约束项目调度问题（resource constrained project scheduling problem，RCPSP）是指在可再生与不可再生资源的约束条件下，根据活动的优先关系计算项目的最小完工时间［1］，其在项目管理、施工和生产计划等诸多领域［2］备受关注。

求解RCPSP主要采用精确算法和启发式算法。精确算法包含分支定界［3］、分支裁剪［4］和基于事件的方法［5］。受限于计算复杂度和NP-hard等因素，精确算法仅适用于解决小规模问题，截至目前，最好的精确算法也只能在实例不受高度资源约束的情况下解决最多涉及60个活动的项目［6］，但现实中项目数往往超过这个规模，且要求解决方案必须快速确定，所以针对RCPSP的研究重心集中在启发式算法领域，以期在准确性、计算速度、简化操作和灵活性之间寻找最佳的平衡［6］。R.Zamani［7］提出了一种基于磁铁 分频算子的遗传算法，通过局部搜索提高算法的性能；还提出了基于遗传算法和隐式枚举搜索技术的算法［8］，可有效提高算法的计算速度，并易于得到更优的解集；S.Elsayed等［9］提出了一种基于双算子的综合进化算法，其中的元启发式算法自适应选择，可避免算法陷入局部最小值；JIA Q等［10］提出了一种改进的粒子群优化算法，该算法使用排序优先技术表示粒子，并基于双对齐的局部搜索技术改进算法的求解，在解决项目调度问题库（a project scheduling problem library，PSPLIB［11］）

中的问题时，该算法的性能优于其他PSO变体；A.Thammano等［12］提出了一种基于遗传算法的综合方法，该综合方法将禁忌搜索［13-14］和模拟退火［15］应用于小部分种群中，以减少计算时间；E.Rashedi等［16］提出了引力搜索算法（gravitational search algorithm，GSA），该算法以自然界中常见的万有引力现象为灵感，将其转化为随机搜索最优解的过程，利用个体间的引力实现群体间的信息交互，从而找到最优解。

引力搜索算法因其流程简单、参数较少、易于实现等特点，在已有的启发式算法中脱颖而出，目前已广泛应用于不同类型问题的优化求解。然而，引力搜索算法也存在不足，如容易陷入局部最优和精度不高等，且算法的收敛性易受到迭代次数的影响，导致计算成本较高。

鉴于此，为了更有效地求解RCPSP，得到项目的最小完工时间，本文将向心力概念引入GSA中，以有效平衡粒子的探索能力与开发能力，且避免算法陷入局部最优；同时，将Logistic混沌映射引入到RCPSP求解，通过Logistic映射得到的混沌序列具有随机性和不可预测性，这两种性质可以增加算法找到最优解的概率，避免陷入局部最优解。

1 问题描述

RCPSP中，假定所有活动和优先约束均已知，且必须实现所有活动［17］，每个活动的执行均须遵循优先关系与资源约束，其中优先关系是指活动j必须要等到其所有的前置活动pred（j）结束之后才会被执行。

RCPSP的基本描述如下：项目由非循环节点活动（activity-on-node，AON）网络拓扑表示。网络拓扑结构包含（N+2）个活动，其中第一个和最后一个活动分别表示开始和结束活动，称为虚拟活动，不占用时间和资源。所有活动共享R种可再生资源，其中第k种可再生资源的可利用总量为Rk（k＝1，2，…，R）。第j个活动的持续时间为dj，对资源k的需求量为rjk。此外，所有参数的值均为非负整数。单模的RCPSP数学模型为

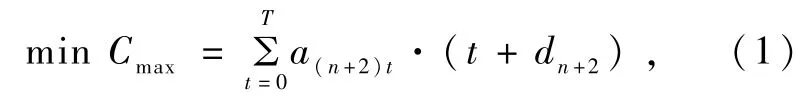
约束条件为

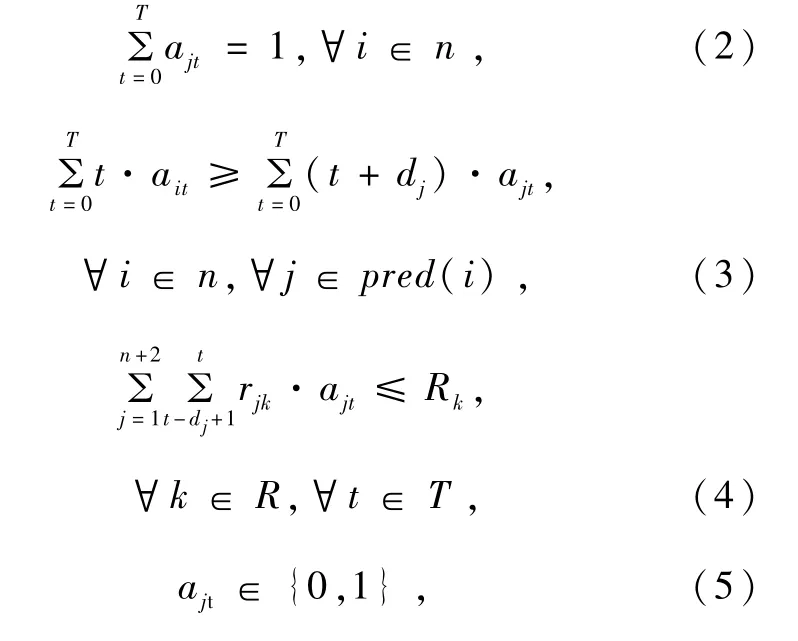
决策变量ajt定义为

RCPSP的目标函数为最小完工时间，即式（1）中的Cmax；式（2）保证每个活动只能被执行一次；式（3）保证活动i在其所有前置活动完成前不能开始执行；式（4）确保活动必须在其所需的可再生资源可用时执行。

2 求解RCPSP的引力搜索算法

2.1 算法简介

引力搜索算法的灵感来源于万有引力定律和牛顿第二定律。依照万有引力定律，搜索空间中的各个粒子之间存在相互作用力并在万有引力的作用下朝着质量较大的粒子方向移动。同时，搜索空间中个体的运动遵循牛顿第二定律。随着算法不断迭代，最终整个种群会聚集在质量最大的个体周围，找到的质量最大个体即为全局最优解。因此，根据引力搜索算法，可将求解最大值优化问题转化为在搜索空间中搜索质量最大的个体问题。

相较于其他元启发式优化算法，GSA算法具有较强的全局搜索能力且操作简单、易于扩展。但GSA算法的收敛性会受到迭代次数的增加而降低，并有陷入局部最优的倾向，而且当涉及到矩阵运算时GSA算法计算成本较高。针对该问题，提出改进的引力搜索算法（improved gravitational search algorithm，IGSA），该算法将向心力概念引入GSA，可有效避免算法陷入局部最优并提高求解精度。

IGSA算法中，向心力大小与物体质量、线速度成正比，与物体间距离成反比。质量越大，行星朝太阳运动的速度越快，能更快地找到最优解。同理，线速度越大和距离越小也能达到这种效果。

向心力公式为

式中：F为物体之间的向心力；M为物体质量；V为线速度；R为两者之间的距离。

根据式（7），得到线速度V表达式，即

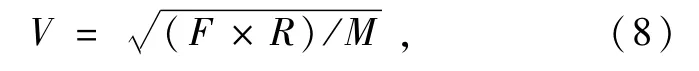
为方便计算，将线速度V表达式更新为

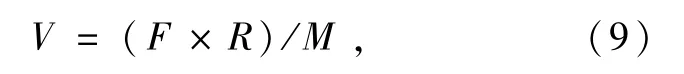
根据式（9），迭代过程中速度更新公式为

式中：fit为当前搜索代理的适应值；fitg为迭代过程中的最优适应值；Dis（x，xg）为当前搜索代理与全局最优搜索代理之间的距离。

根据速度表达式，可得到位置更新公式，即

为了更全面描述搜索过程，该算法将寻找最优解的过程分为勘探阶段，开发阶段和避免陷入局部最优解阶段。勘探阶段为两个物体在向心力作用下做近似圆周运动；开发阶段为随着迭代次数增加，物体之间的距离逐渐缩小；避免陷入局部最优解阶段物体之间的距离为定值。开发阶段式（11）可提高算法的收敛速度，并避免陷入局部最优。

2.2 相关机制

在求解RCPSP过程中，调度生成机制与邻居生成机制必不可少。此外，为进一步提高寻优的效率和效果，在求解过程中引入混沌机制，增强算法的多样性。多样性是指在生成解决方案后算法有一定的概率可重新执行插入操作或交换操作，执行完此变异操作后，算法可能会得到更好的解决方案和更优的最小完工时间。

2.2.1 调度生成机制

调度生成机制通过给定的优先级列表为每个活动分配开始时间，从而确定可行的调度。该机制主要包括串行调度和并行调度。本文采用每次执行一个活动的方式依次调度，隶属于串行调度。

串行调度方案通过阶段式的扩展部分调度表生成可行调度方案，其中部分调度表是指只有一部分活动被分配完成时间的调度表［18］。在每个阶段，调度生成方案得到所有可调度活动的集合称为决策集，然后使用特定的优先级规则，从决策集中选择一个或多个活动进行调度，最终得到调度结果。串行调度的具体步骤如下。

（1）初始化，n＝1。

（2）计算可调度活动决策集合Dn。

（3）选择Dn中具有最高优先权值的活动i，同时获取该活动i的持续时间di和在t时间资源r的剩余量（t＝1，2，…，T；r∈R，t为当前时刻，T为总时间）。

（4）从已调度集合Sn中获取活动i的所有前置活动中的最迟完成时间，并将其作为i的最早可能开始时间ESi。

（5）计算活动i在满足时序和资源约束条件时的最早开始时间Si，并计算活动i的完成时间Fi。

（6）将活动i从Dn中删除，同时更新Sn+1。

（7）n＝n+1。

（8）若n值不大于活动数，则跳至步骤（2）。

2.2.2 邻居生成机制

当前解决方案的邻居可通过插入或交换操作得到。当执行完插入或交换操作后，可能会违反优先规则和资源约束，所以需要重新对新的解决方案进行串行调度操作使其可行。下面以一个具体实例说明插入和交换操作。表1为当前解决方案，图1和图2分别表示对当前解决方案执行插入和交换操作。

表1 当前解决方案Tab.1 Current solution

假设实例共9个活动，对表1所示的解决方案分别执行插入和交换操作。

（1）插入操作：选择活动5执行插入操作，使其移动到新的位置。在活动5的最后一个前置活动2和最早的后继活动8之间随机选择一个活动，以活动8为例，得到此活动的位置为6，即将活动5插入位置6，并依次移动活动8和活动7的位置，最终结果如图1所示。

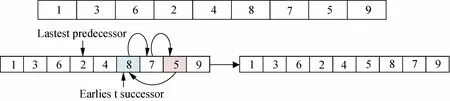
图1 插入操作示例Fig.1 Insert operation example

（2）交换操作：选择活动4执行交换操作。在活动4的最后一个前置活动2和最早的后继活动7之间随机选择一个活动，以活动3为例，得到此活动的位置为2，即将活动4交换到活动3的位置2，活动3交换到活动4的位置5，其他活动位置不变。最终结果如图2所示。

图2 交换操作示例Fig.2 Exchange operation example

2.2.3 混沌机制

混沌映射用于生成混沌序列，是一种由简单的确定性系统产生的随机性序列，具有非线性、随机性、遍历性和长期不可预测性等特征。常见的混沌映射有Logistic映射、Gussian映射、Singer映射等。本文选用简单易用的一维Logistic混沌映射，其数学表达式为

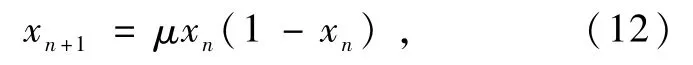
式中：n为迭代次数；μ∈［0，4］，为Logistic控制参数；x∈（0，1）时，Logistic映射处于完全混沌状态。

图3表示初始值x0一定时，随着控制参数μ取值变化，迭代过程中可得到的取值范围。由图3可以看出，在μ越接近4的地方，x取值范围越是平均分布在0到1的区域。图4表示初始值x0为0.5，迭代次数为300，控制参数μ分别为2.5与3.98时x的取值范围。由图4可以看出，μ3.98时迭代生成的值处于随机分布状态，μ2.5时，经过一定次数的迭代后，生成的值将收敛到一个特定的数值。

图3 控制参数取值Fig.3 Value of the control parameter

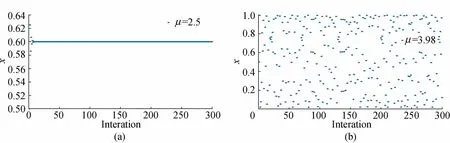
图4 不同控制参数迭代后的值Fig.4 Values of different control parameters after iteration

2.3 求解步骤

基于上述3种机制和算法，改进的引力搜索算法解决RCPSP的步骤如下。

（1）初始化种群数量n、最大迭代数MaxIt、Logistic控制参数μ和初始值x0。

（2）随机初始化，并对初始化后的解执行串行调度操作使其可行。

（3）生成新的解。按照式（10）和（11）得到步长stepsize。若0＜stepsize≤0.3，对当前解执行插入操作；若0.3＜stepsize≤1，对当前解执行交换操作。生成的新解可能会违反优先规则或资源约束，所以需要对新解执行串行调度操作使其可行。

（4）评估质量。根据优先规则和资源约束得到最佳适应度的值Cmax。若解的适应度值Fj＞Cmax，更新此解的适应度值；若解的适应度值Fj＝Cmax，计算平均资源利用率，将资源利用率更高的保存在迭代中。

（5）多样化。分别使用随机函数与混沌机制中的式（12）生成0～1的参数K和Pa，若K＞Pa，则对相应的解进行交换操作得到新的解并对新解重新评估质量。

（6）当相对误差MPE的值为0或达到最大迭代数MaxIt时，输出Cmax和对应的调度方案，否则跳到上述（3）。

3 结果与分析

为了评估IGSA算法求解RCPSP的效果，选择PSPLIB数据集进行对比实验。PSPLIB数据集包含难易程度不同的调度问题实例，这些实例根据每个项目所包含的活动数量分为几组，包括J30，J60，J90和J120基准测试问题集等。对于该数据集，测试集中包含了每个项目的最优解，称之为参考值。对比算法包括粒子群优化算法（particle swarm optimization，PSO）、布谷 鸟 搜 索 算 法（cuckoo search，CS）、GSA和无混沌机制的IGSA（NCM-IGSA）。

为了保证实验结果的准确性，对所有的对比算法设置种群数量n为25，最大迭代数MaxIt为400。PSO，CS算法，GSA和NCM-IGSA中的参数Pa为固定值0.25，IGSA的Logistic控制参数μ为4和初始值x0为0.6，PSO算法的速度和位移公式由式（13）～（14）表示，GSA的引力常量G随着迭代增加而减小，计算如式（15）所示。通过与测试集中的参考值进行比较，使用相对误差（MPE）、最优值（best cost，BC）衡量算法的性能，其中相对误差MPE的值等于［（算法求得的最优解-参考值）／参考值］。除此之外，为了使实验结果更严谨，将数据集中的实例运行10次，得到平均值（AVG）并进行比较。选择的测试集为PSPLIB中的J3001_01，J6001_01，J9001_01，J12001_01，其参考值分别为43，77，73和105。实验结果如表2所示。

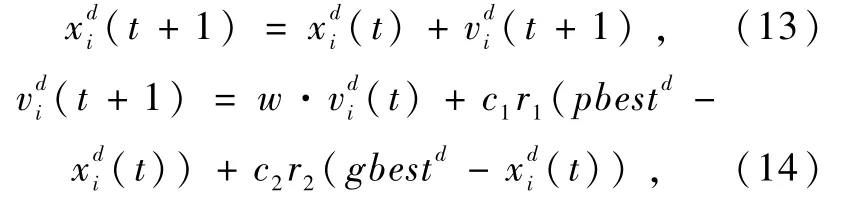
其中，式（13）和（14）分别为在t时刻d维空间中第i个粒子的位置与速度更新公式；w为惯性权重，取w＝1；c1与c2为两个加速度系数，用于平衡个人经验和社会经验，一般取c1＝c2＝2；r1和r2为［0，1］内均匀分布的随机数；pbestd为到目前为止第i个粒子在d维空间中搜索到的最好位置；gbestd为整个粒子群搜索到的全局最优位置。

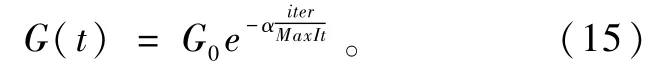
式中：G0为100；α为20；iter为当前迭代次数；MaxIt为最大迭代数。

由表2可以看出，PSO，CS，GSA，NCM-IGSA和ICF-GSA 5种算法在测试集J3001_01上皆能达到最优值43，相对误差均为0，但每个算法运行10次后求得的平均值分别为43.6，43.4，43.6，43.4，43.2，由此可见，ICF-GSA算法相较于其他对比算法得到最优解的概率更高。所以在解决活动数为30的小规模问题时，ICF-GSA的效果优于其他4种算法。

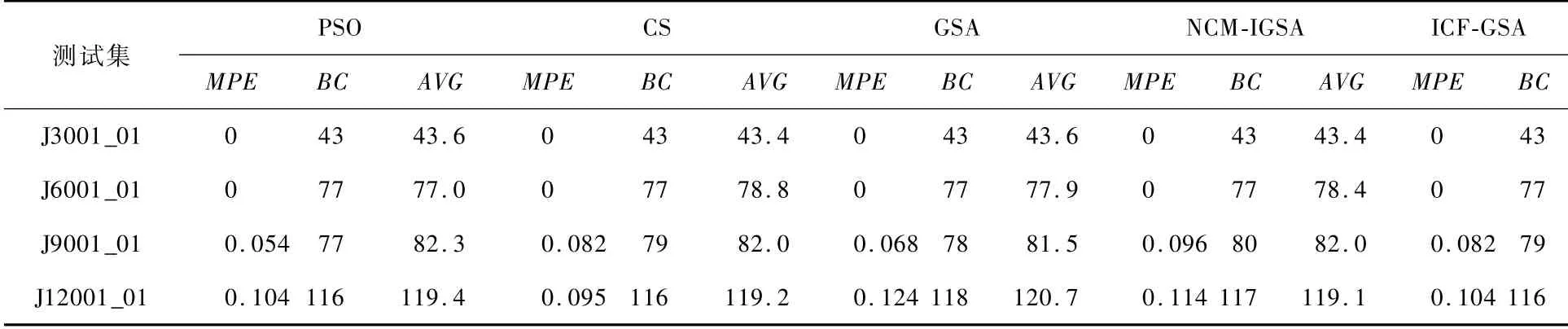
表2 实验结果Tab.2 Experimental results

在活动数为60的中规模调度问题的测试集J6001_01上，5种算法均能得到最优解，相对误差均为0，但CS，GSA，NCM-IGSA 3种算法的平均值分别为78.8，77.9和78.4，而PSO和ICF-GSA的平均值为0，说明这两种算法运行10次后的结果皆为最优值77，所以在解决中规模问题时，PSO和ICF-GSA算法效果优于其他3种对比算法。

在解决活动数为90和120的较大规模调度问题测试集J90001_01和J12001_01时，5种算法均未能达到参考值。虽然PSO算法和CS算法得到的最优值与IGSA相同，都更接近于参考值，但IGSA的平均值小于PSO算法和CS算法。综上可知，IGSA在求解RCPSP时较为有效，易于得到较好的调度结果。

3.1 资源利用率分析

资源利用率可评估算法在最小完工时间内的资源利用情况，避免资源浪费。取每个算法运行10次实例结果中的1次，以测试集J3001_01和J12001_01为例，分析PSO，CS，GSA，NCM-IGSA和IGSA在最小完工时间（最优值）内的资源利用率，实验结果分别如图5～6所示，其中最大资源利用率设置为1，红色实线表示0.8，紫色点划线表示0.6。

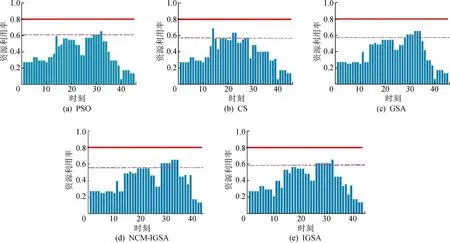
图5 不同算法在测试集J3001_01上的资源利用率Fig.5 Resource utilization of the different algorithm on the test set J3001_01

当测试集为J3001_01时，5种对比算法得到的最优值分别为45，45，45，43和43。由图5可以看出，在最优值的时间范围内，PSO，CS，GSA，NCM-IGSA和IGSA 5种算法资源利用率超过0.6的分别有5份、3份、7份、7份和7份，占总时间的11%，6%，15%，16%和16%，所以NCM-IGSA和IGSA算法能更好地利用资源；当测试集为J120001_01时，5种算法得到的最优值分别为124，121，120，124和116，同理，由图6可以看出，测试集为J12001_01时，5种对比算法资源利用率超过0.8的分别有16份，19份，22份，13份和出，PSO在第90次迭代时得到其最优值45，在第228次迭代时相对误差MPE为0；CS在第91次迭代得到其最优值45，在第266次迭代时相对误差MPE为0；GSA在第105次迭代得到其最优值45，在第279次迭代时相对误差MPE为0；NCM-20份，占总时间的12.9%，15.7%，18.3%，10.5%和17.24%。可见，相比其他算法，GSA和IGSA更能充分利用资源，避免造成资源浪费。

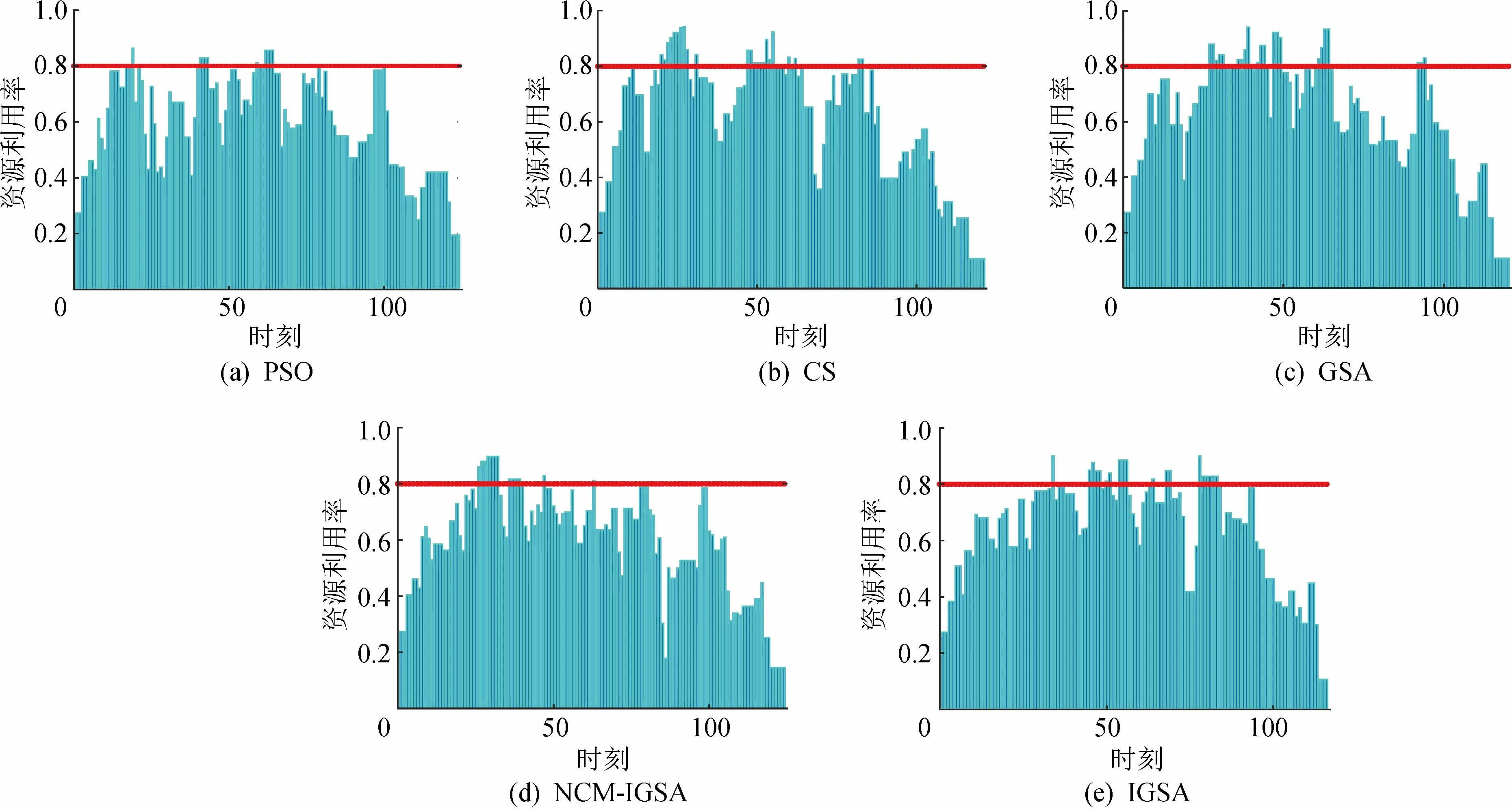
图6 不同算法在测试集J12001_01上的资源利用率Fig.6 Resource utilization of the different algorithm on the test set J12001_01

3.2 收敛性分析

收敛性可衡量算法求解最优值的速度。本文同样以每个算法运行10次实例结果中的1次且测试集为J3001_01和J6001_01为例，以最优值与MPE为度量指标，每种算法迭代400次，分析PSO，CS，GSA，NCM-IGSA和IGSA 5种算法收敛到最优解与相对误差为0的速度。实验结果如图7～8所示。

当测试集为J3001_01时，5种算法得到的最优值分别为45，45，45，43和43。由图7可以看IGSA在第120次迭代得到其最优值43，在第294次迭代时相对误差MPE为0；IGSA经过53次迭代得到其最优值43，在第209次迭代时相对误差MPE为0。相较于其他对比算法，IGSA在解决小规模调度问题时能更快收敛到最优值。

图7 测试函数为J3001_01时的收敛曲线Fig.7 Convergence curves with the test function of J3001_01

当测试集为J6001_01时，5种算法得到的最优解皆为77，由图8可以看出，PSO在第36次迭代得到其最优值77，在经过313次迭代后相对误差MPE的值为0；CS在第27次迭代得到其最优值77，在经过223次迭代后相对误差MPE为0；GSA在第209次迭代得到其最优值77，在经过367次迭代后相对误差MPE为0；NCM-IGSA在第108次迭代得到其最优值77，在第259次迭代时相对误差MPE为0；IGSA在迭代刚开始时即能得到最优解77，且在第170次迭代时相对误差MPE为0。相对于其他算法，IGSA在解决中规模调度问题时也能更快收敛到最优值。这意味着IGSA能够在搜索空间中快速找到最优解，并有效避免陷入局部最优，提高了算法的收敛速度。

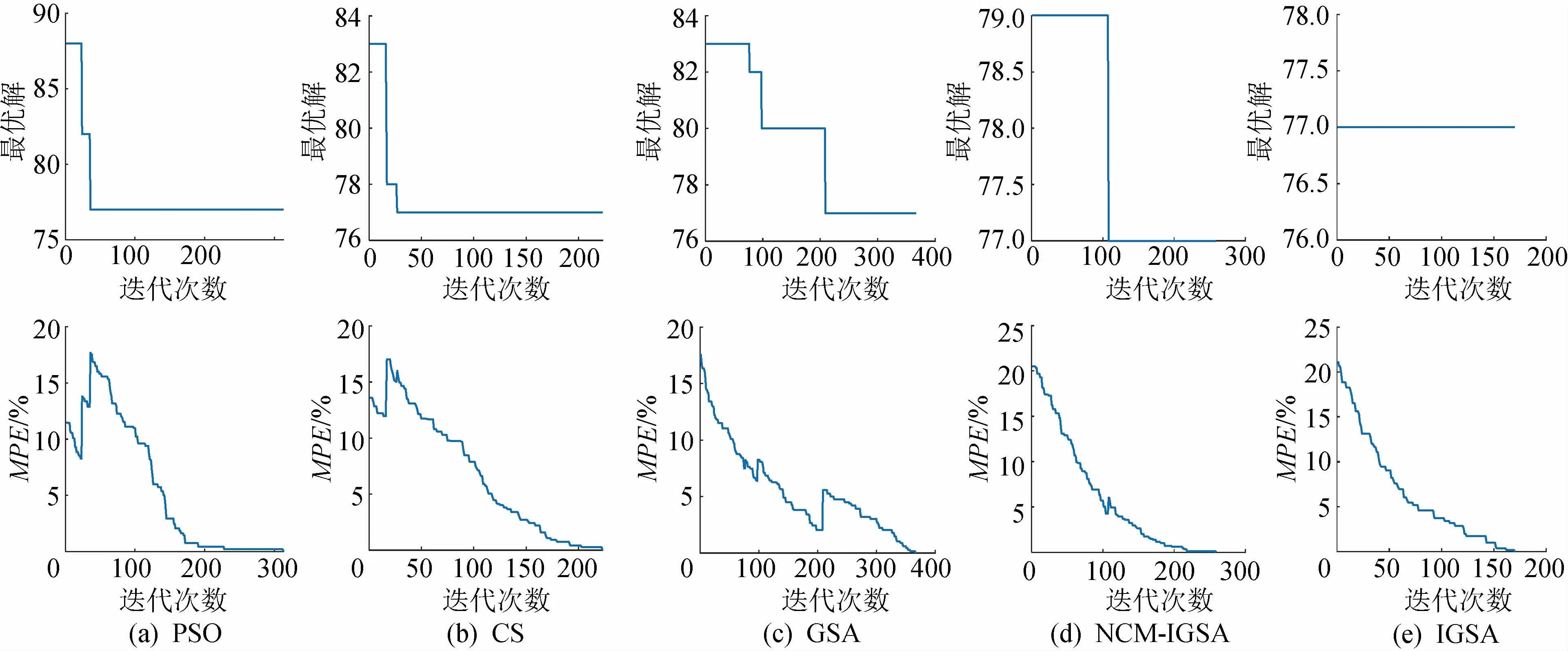
图8 测试函数为J6001_01时的收敛曲线Fig.8 Convergence curves with the test function of J6001_01

4 结 语

为了提高引力搜索算法的收敛速度并避免陷入局部最优，本文在该算法的基础上引入向心力，并在求解RCPSP的过程中加入混沌机制，提出改进的引力搜索算法IGSA。为了评估算法的优化表现，在PSPLIB问题实例J30，J60，J90和J120上进行了实验。实验结果表明，在解决RCPSP问题时，相较于其他算法，IGSA得到的最优解更接近于测试集的参考值，在资源利用和收敛性方面也优于其他算法。