基于小波分解与恒星日滤波的BDS多路径削减方法
杨威,张秋昭,马晓东
(1.中国矿业大学 环境与测绘学院,江苏 徐州 221116;2.中铁大桥勘测设计院集团有限公司,湖北 武汉 430051)
0 引 言
随着科学技术与工程技术发展,国内大型复杂结构建筑数量不断增加,传统变形监测方法局限严重,应用全球卫星导航系统(global navigation satellite system,GNSS)观测技术进行变形监测已成为保证建筑结构健康安全的重要渠道,然而,受轨道误差、电离层延迟、对流层延迟、相位中心偏移与多路径误差等影响,GNSS载波相位测量技术精度一般为厘米级,要达到变形监测的毫米、亚毫米级,必须严格消除误差项。短基线(<3 km)情况下,通过载波相位双差技术可基本消除多路径误差以外的误差项。
国内外学者提出了多种方法降低测站周围环境、卫星测站几何结构对多路径误差的影响。除改进天线和硬件外,还改进了数据后处理方法,常用的数据后处理方法包括信噪比法[1]和恒星日滤波法[2]。然而,信噪比与多路径效应影响之间存在时间差且无法量化[3],具有一定局限性。文献[4]发现在测站恒定不动且周围环境不变时,卫星与地面测站及周围反射面的几何构型具有周期重复性。J.F.Genrich等[5]依据这一特征首先提出恒星日滤波法(sidereal filtering,SF),由此逐渐发展出基于观测值域和坐标域的SF[6-8]。利用坐标域SF对首次观测解算坐标提取多路径误差序列,并以此对重复观测定位结果进行修正,容易实现且计算简单。但该方法采用平均星下点周期,忽略了卫星间的差异性,无法有效应用于具有3种不同类型轨道的北斗卫星导航系统(Beidou satellites navigation system,BDS)多路径缓解中[9]。观测值域SF通过对首次观测值提取单差残差或双差残差,再对每颗卫星残差进行滤波处理得到各卫星的多路径误差序列,然后对每颗卫星观测值域进行改正[10]。该方法考虑了每颗卫星重复周期不完全相同的特点,适应性强,计算相对复杂。此外,在应用SF提取多路径误差序列时,还要采用合理的滤波方法,常用的滤波法有小波滤波[11]、EMD滤波[12]、Vondrak滤波[13]等。
由于BDS独特的星座设计,众多学者发现BDS卫星的多路径效应特征显著不同于其他系统的,因而进行了大量研究。WU X L等[14]提出一种缓解IGSO卫星和GEO卫星伪距多路径的方法;MA X等[15]发现BDS系统GEO卫星观测值的多路径效应呈低频变化特征,而IGSO卫星和MEO卫星主要呈高频变化特征;YE S等[9]研究了BDS卫星多路径重复周期,并提出了BDS系统的载波相位多路径消除方法;DONG D N等[16]提出了多路径半天球图(multipath hemispherical map,MHM),实现了多路径效应的实时在线解算和改正;DAI W等[17]对MHM算法和恒星日滤波算法进行了对比分析,提出了多路径误差参数化改进模型。
本文针对BDS系统星座特性,提出一种恒星日滤波与小波结合的多路径削减方法,该方法基于重构后的载波相位和伪距单差残差提取多路径误差序列,对每颗BDS卫星分别进行多路径误差改正,采用单频单历元LAMBDA算法解算基线处理实测数据。结果表明该方法能有效削弱多路径误差,提高定位精度。
1 多路径误差理论
多路径效应引起的路程差[10]可表示为

式中:D为接收机天线与反射体间的水平距离;θ为反射信号的入射角;λ为信号波长;α为测站周围反射体的反射系数;Δφm为多路径效应引起的相位延迟量。
由式(1)可知,多路径误差的大小受反射体反射系数、反射信号入射角和反射体到接收机天线的距离等因素影响。静态基线下,反射系数与距离可认为不变,入射角则与卫星相对地面的运行轨迹密切相关。而卫星相对地面的运行轨迹是周期重复的,所以多路径误差也应随卫星运行轨迹周期变化。
2 BDS卫星星下点重复周期
由于卫星多路径误差变化具有周期性,研究中可利用首次观测提取出的多路径误差序列改正重复观测数据,卫星的多路径周期应与其星下点周期一致,因此必须计算出每颗卫星的星下点周期。对于BDS系统的3种卫星,GEO卫星和IGSO卫星的星下点轨迹周期约为1 d,而MEO卫星的星下点轨迹周期约为7 d。由于周期近似于整数天,需要求出每颗卫星重复周期的时间提前量。根据广播星历给出的轨道半径与角速度改正,求出该时刻的卫星运行角速度
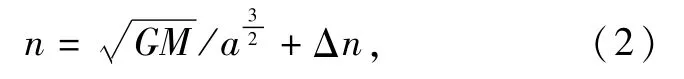
对于GEO卫星和IGSO卫星,时间提前量
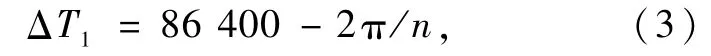
对于MEO卫星,时间提前量

以2017年1月和2月的BDS星历数据为基础,从中提取所有历元时刻的相关轨道参数,参照式(3)~(4),求出所有观测到的卫星在各个星历时刻所对应星下点周期的时间提前量,见图1~3。

图1 GEO卫星时间提前量Fig.1 Time advance of GEO satellite
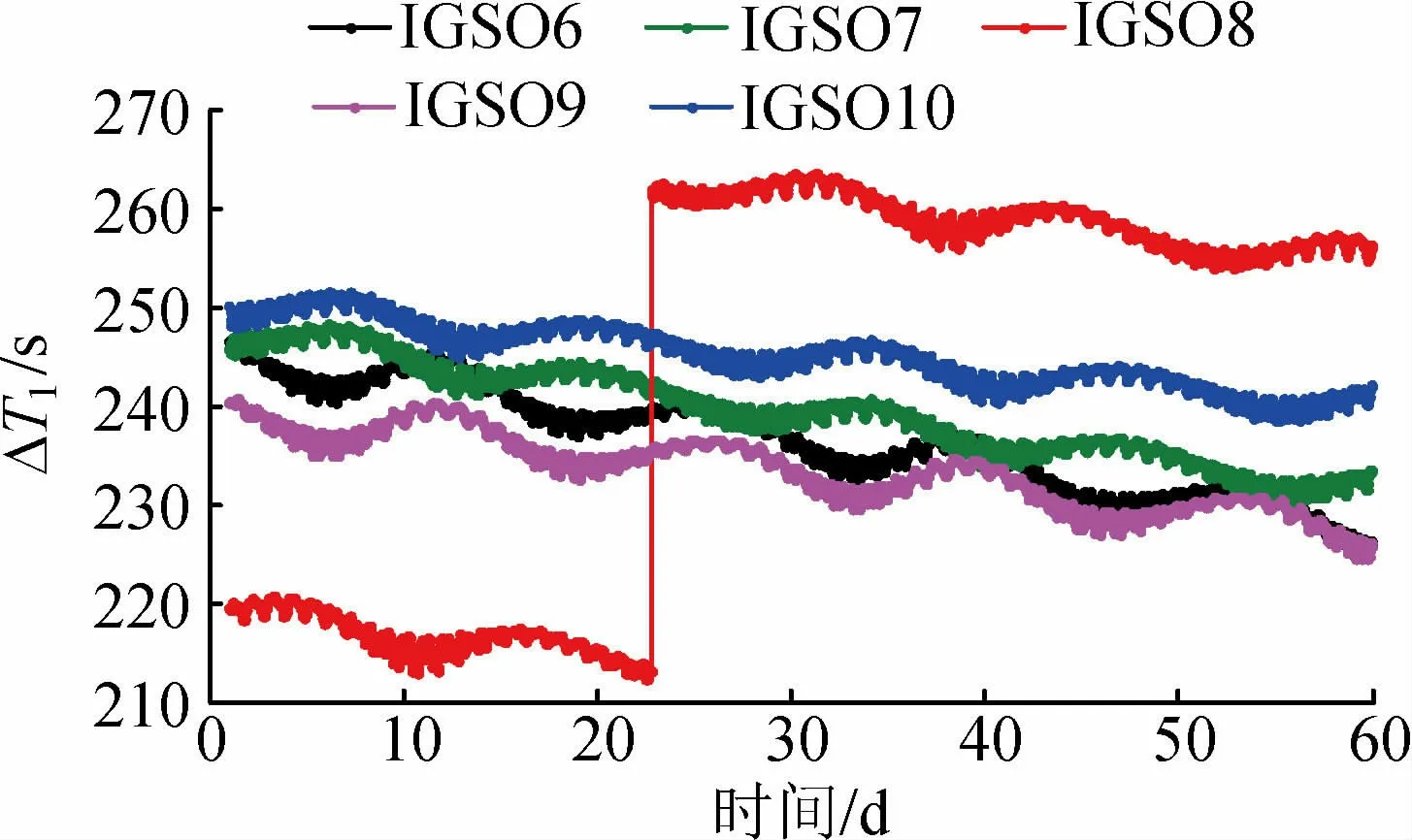
图2 IGSO卫星时间提前量Fig.2 Time advance of IGSO satellite
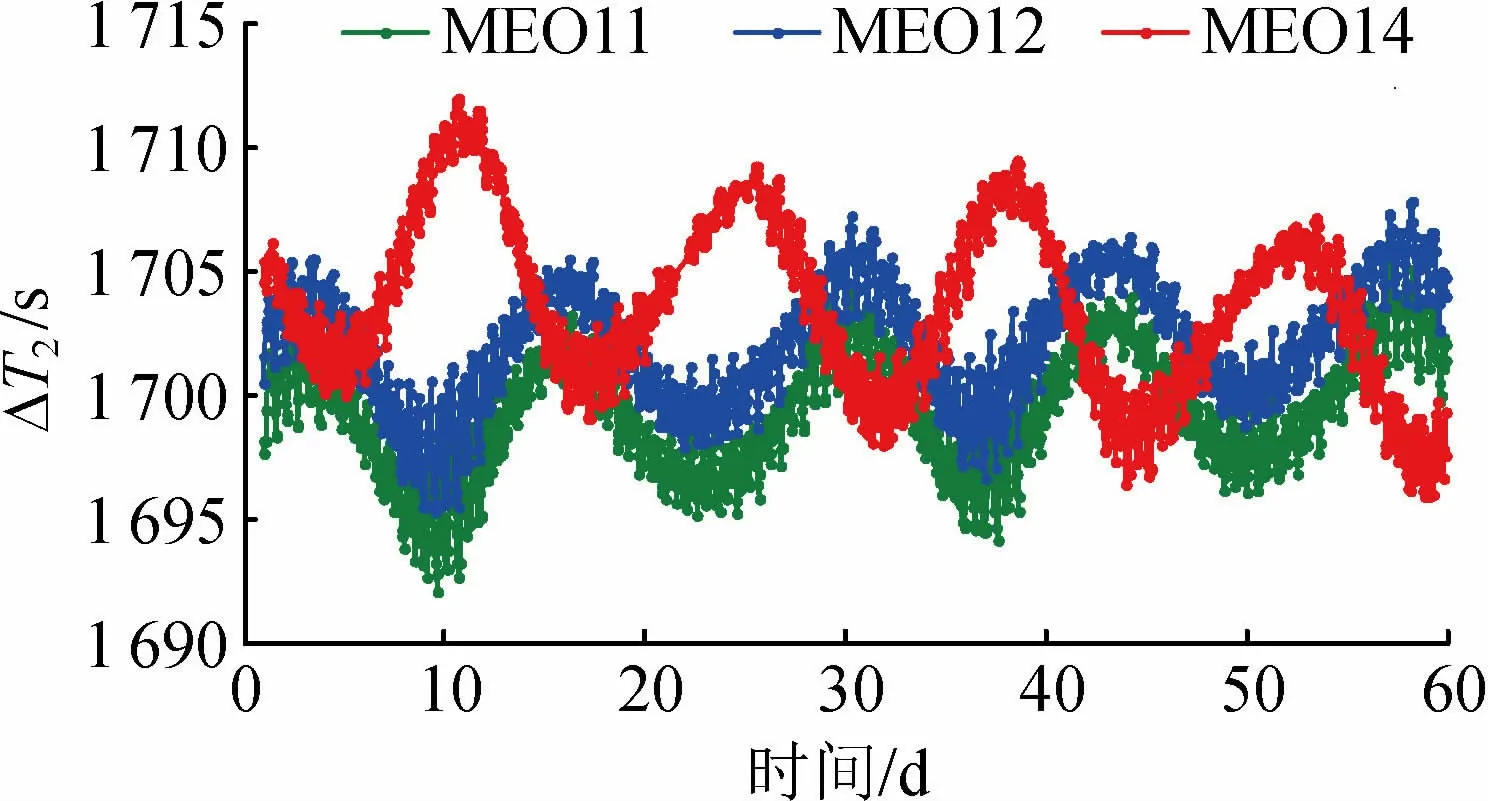
图3 MEO卫星时间提前量Fig.3 Time advance of MEO satellite
由图1~3可知,3种不同类型的卫星对应的平均时间提前量各不相同,同一类型的卫星对应的时间提前量也不一样,即便是同一颗卫星在不同时间段的时间提前量也不同,所以修正多路径误差不仅要精确到单颗卫星,还要精确到每颗卫星的对应时刻。
3 单差残差重构
短基线双差伪距和载波相位观测方程为
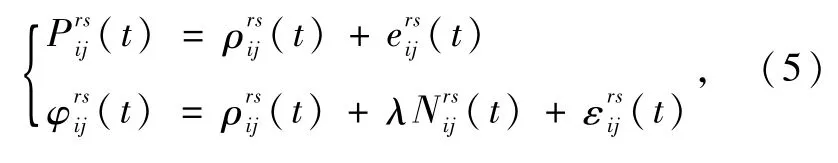
设静态模型下可观测卫星颗数为m,则单频单历元可得到2(m-1)个双差方程,将近似值归入观测值并线性化可得

其中,x和y分别为双差模糊度和双差基线向量,A和B分别为二者的系数阵,l为伪距和载波组合双差观测值,dd为双差残差项。
短基线双差基本可以消除钟差、电离层延迟、对流层延迟和星历误差,所以双差残差项残余主要为多路径误差。由于双差过程中基准星为最大高度角卫星,并非恒定卫星,造成部分卫星的部分历元双差残差项缺失,可以通过反求单差残差规避。由单差到双差的转换过程为

其中,sd为单差残差,D为转换矩阵,且为奇异矩阵,无法求逆。
为解决D无法求逆这一问题,采用C.Albe等[18]在2000年提出零均值假设,即,使矩阵D变为非奇异矩阵,则式(7)可以写为
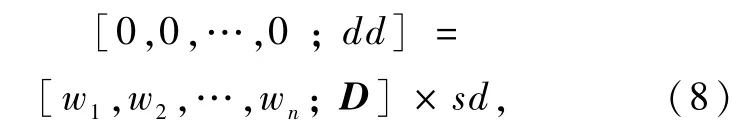
其中,wi为控制条件方程质量的关键因子,即观测值的权,该值受观测值自身质量影响。本文采用高度角定权的方式确定权阵大小,即wi=sin2(θ)。则单差残差可重构为
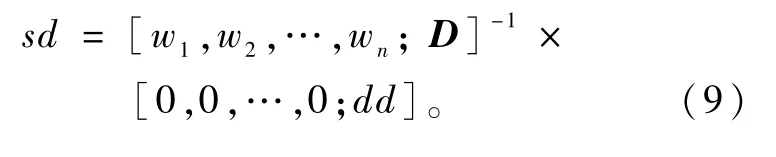
4 单频单历元BDS多路径的SF算法
考虑到BDS卫星重复周期的差异性,应基于观测值域进行恒星日滤波。对于单频单历元载波相位解算,观测方程必须包括伪距方程,否则会造成秩亏,因此应同时对载波和伪距方程进行去多路径处理。其主要步骤如下。
(1)以解算结果的均值x作为基线向量的已知解,将其带入第一次观测数据解算,反算整周模糊度并取整得y,将x和y回带到式(2)得到双差载波和伪距观测值残差v。
(2)利用式(6)将双差观测值残差转换为单差观测值残差。
(3)使用小波滤波方法分解单差残差项,提取每颗卫星的载波和伪距多路径误差序列。
(4)基于第一次观测数据的广播星历计算每颗卫星的时间提前量,根据时间提前量调整单差残差多路径误差时间序列并转化为双差序列。
(5)从第二次观测数据双差方程的残差项中减去双差残差多路径序列,用LAMBDA算法单频单历元解算基线。
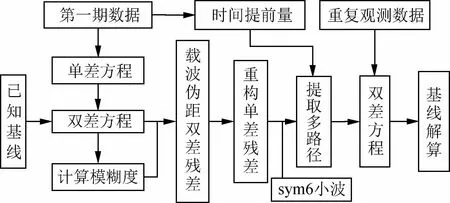
图4 单差残差恒星日滤波算法流程Fig.4 Flow of single difference residual sidereal filter algorithm
5 多路径误差改进试验
采用一组实测单频数据验证本方法,数据采集时间为2016年9月9日至26日,每日采集4 h BDS数据,采样频率为1 s,地点为江苏省徐州市中国矿业大学环测楼楼顶,接收机型号为天宝R10,主站安置于无遮挡无多路径环境并开启接收机多路径抑制功能,移动站周围模拟多路径环境,并关闭接收机多路径抑制功能。以其中17,23和24日的数据为基础进行改正和展示。
5.1 计算重复观测提前量
观测时期C01~C05为GEO卫星,C06~C10,C15为IGSO卫星,C11,C12和C14为MEO卫星。根据DBS卫星星下点重复周期可知,9月24日1~10号和15号卫星的时间提前量应为9月23日对应时间段的广播星历计算的平均值,9月24日11,12,14号卫星的时间提前量应为9月17日对应时间段的广播星历计算的平均值,其计算结果如表1所示。

表1 9月24日BDS卫星重复观测提前量Tab.1 Advances of repeated observation of BDSsatellite on September 24
5.2 单差残差
采用单差残差重构步骤,提取17,23和24日每颗BDS卫星的单差残差序列,受篇幅所限图5~7仅给出C01,C06和C14卫星的载波相位单差残差,图8为C14卫星的伪距单差残差,采用相关系数法分别求取每颗卫星17与24日、23与24日的单差残差序列的相关性与错位时间的关系曲线(即遍历计算两个序列错位[-10 000~1 000]s的相关系数值),其最大相关值点为重复观测提前量。表2给出示例卫星分别在17—24日和23—24日多路径误差曲线的最大相关值及其对应的重复观测时间提前量。
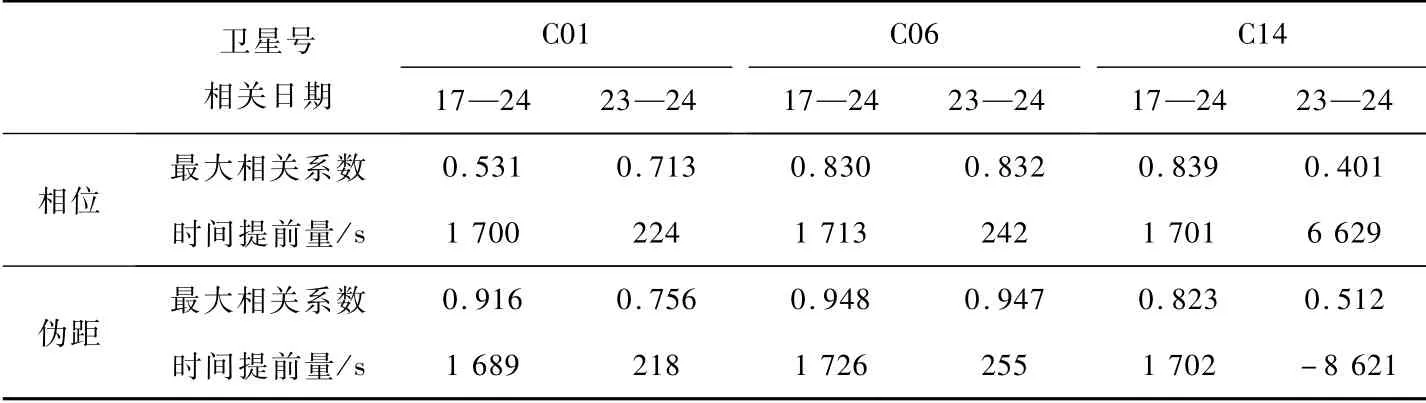
表2 C01,C06,C14卫星单差残差序列相关性与时间提前量Tab.2 Correlations and advances of C01,C06,C14 single difference residual sequence
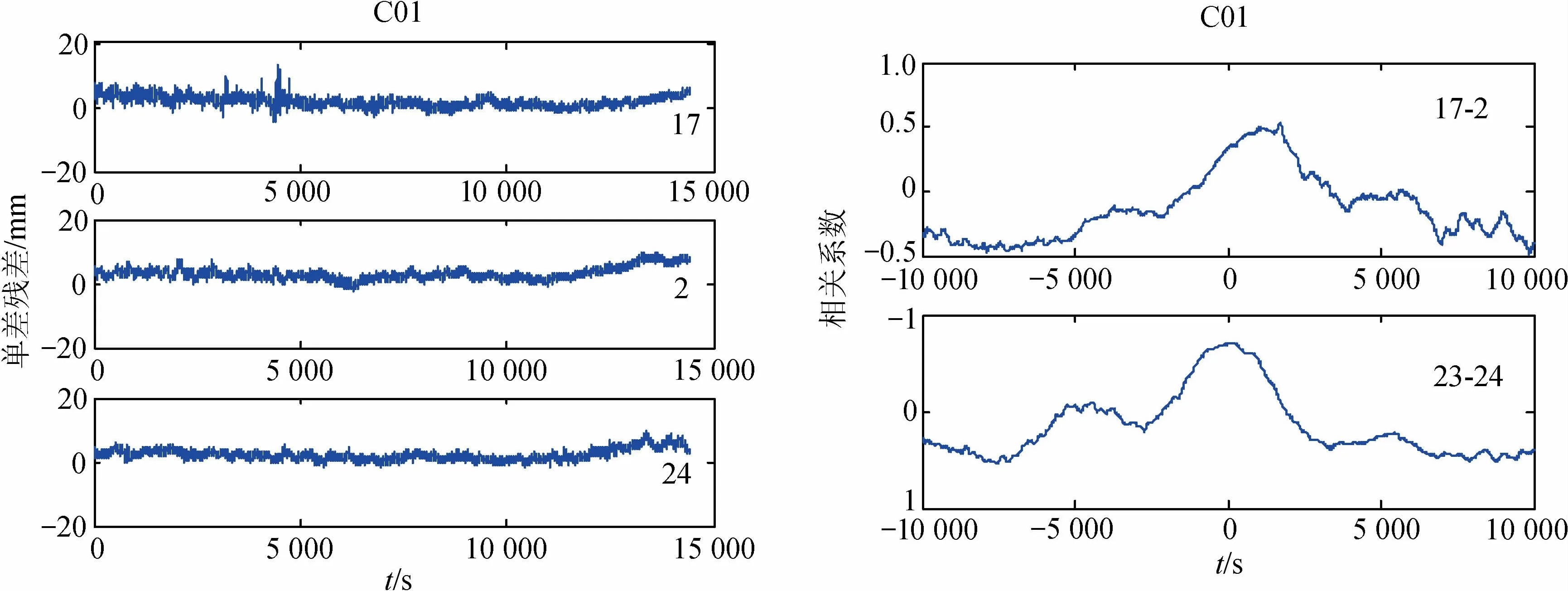
图5 1号GEO卫星载波单差残差序列及相关系数Fig.5 Carrier phase single difference residual sequence and correlation coefficient of GEO 01

图8 14号MEO卫星伪距单差残差序列及相关性Fig.8 Code single difference residual sequence and correlation coefficient of MEO 14
根据BDS卫星星下点重复周期可知,GEO卫星和IGSO卫星的星下点轨迹周期均为近1 d,故C01和C06卫星在23—24日的单差残差序列中表现出良好的相关性。C01卫星载波和伪距最大相关系数分别为0.712 7和0.755 7,最大相关处时间提前量分别为224和218 s,与通过星历计算的226 s十分接近。同时C06卫星相位和伪距最大相关系数分别为0.832 2和0.947 4,最大相关处时间提前量分别为242和255 s,与244 s理论值相符。MEO卫星的星下点轨迹周期均约7 d,故C14卫星在17日和24日的单差残差序列中表现出良好的相关性,最大相关系数分别为0.839和0.822 9,最大相关处时间提前量为分别为1 701和1 702 s,与理论值1 704 s相符;23—24日的单差残差序列则并没有明显的同趋性,最大相关系数仅为0.401。
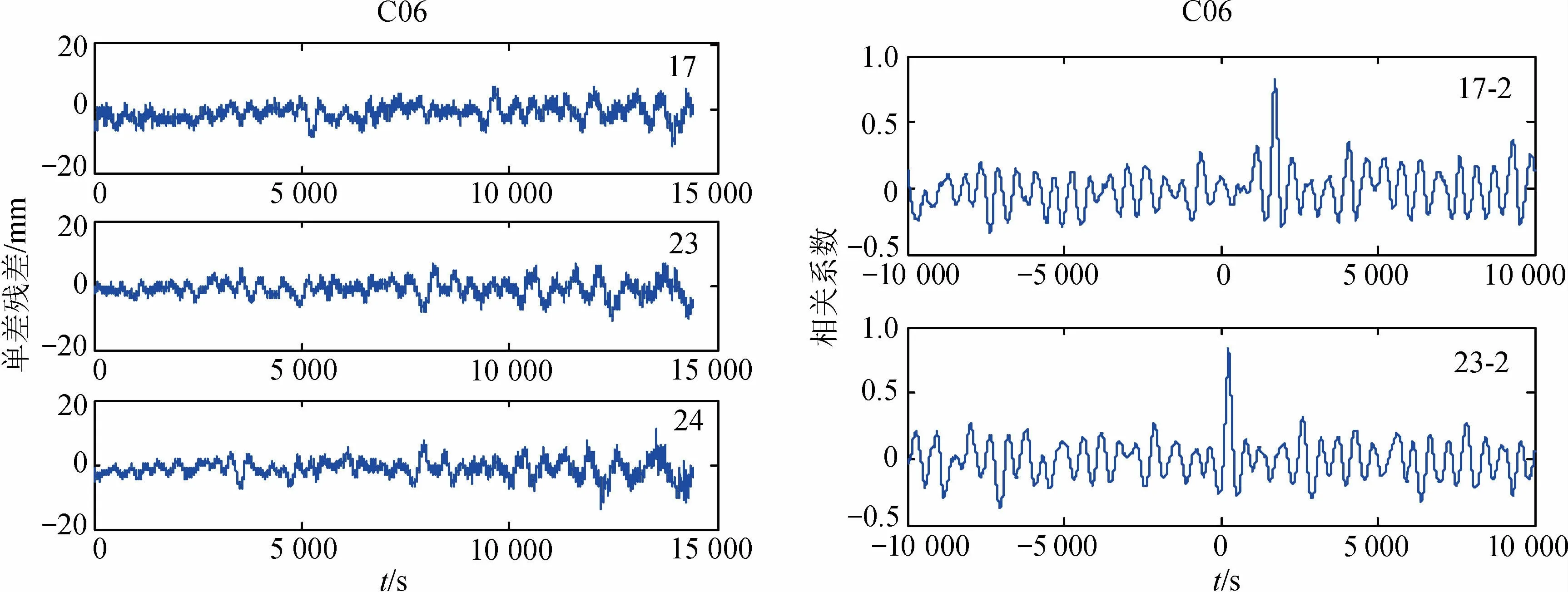
图6 6号IGSO卫星载波单差残差序列及相关性Fig.6 Carrier phase single difference residual sequence and correlation coefficient of IGSO 06

图7 14号MEO卫星载波单差残差序列及相关性Fig.7 Carrier phase single difference residual sequence and correlation coefficient of MEO 14
5.3 sym6小波提取多路径误差
小波滤波器通过伸缩平移变换将信号分解成不同的频率层[19]。文献[20]指出多路径误差主要存在于低频层,而高频层主要包括白噪声或建筑物的高频振动信号,因此需去掉高频部分而保留低频部分,重构原始单差残差序列。对比不同小波基函数对模拟噪声的去噪效果,选取sym6小波提取多路径误差序列,分解级数为4层,选取两层低频的进行重构。
采用sym6小波方法对17日MEO卫星和23日GEO卫星、IGSO卫星的载波和伪距单差残差序列进行分解,将提取的低频部分视为多路径误差。图9为C01,C06和C14卫星的单差残差多路径时间序列。
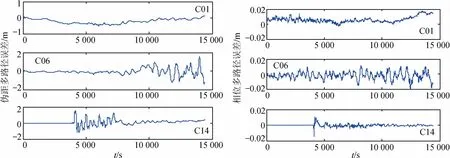
图9 单差残差提取的多路径误差序列Fig.9 Multipath error sequences of single difference residual extraction
5.4 改正多路径误差
根据时间提前量调整17日的单差载波和伪距多路径误差序列,使之与24日观测数据的多路径误差在时间上保持一致。将提取的单差多路径误差转化为双差形式后带入双差方程求解,其转换方程为式(8),相当于双差转单差的逆变换。图10为使用本文方法改进多路径误差前后的E,N,U偏差图,该图以基线解算结果的平均值为参照解,以误差值的标准差为评价标准,表3为E,N,U改进效果。
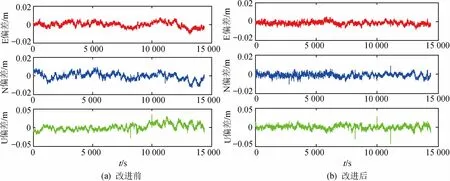
图10 多路径误差改进效果Fig.10 Improvement effects of multipath error mitigation

表3 基线解算E,N,U偏差改进效果Tab.3 Improvement effect of baseline solution deviation of E,N,U directions
如图10所示,左图为改进前的多路径误差基线E,N,U偏差图,右图为改进后的偏差图,改进后的偏差平滑效果明显。由表3可知,改进前的E,N,U偏差分别为2.87,3.59和8.05 mm,改进后相应削弱为1.72,2.03和5.00 mm,精度相应提升了40.1%,43.5%和37.9%。
6 结 语
本文系统阐释了BDS系统3种卫星的星下点重复周期特性,针对由此造成的多路径误差特性,提出了一种应用于BDS卫星多路径削弱的数据后处理方法。该方法基于观测值域重构每颗卫星的相位和伪距单差残差序列,应用sym6小波分解,从中提取多路径误差序列,并将其按提前量调整序列后改正到重复观测数据的相位和伪距方程中,然后使用LAMBDA方法单频单历元解算基线向量。最后,对一组实测数据实施上述方法,结果表明,该方法能有效削弱多路径误差,提高了定位精度,使E,N和U精度分别提升40.1%,43.5%和37.9%。

