多调和算子组主次谱间隙的估计

黄振明

(苏州市职业大学 数理部, 江苏 苏州215104)

众所周知，Riemann流形上最基本的椭圆型算子是拉普拉斯算子Δ，也称调和算子，如果流形是紧致的，则Δ有离散谱，其所有离散谱构成的集合蕴含了流形的重要的几何和拓扑信息。国内外众多学者运用算子法和分析法等多种方法，对调和算子Δ[1-2]、双调和算子Δ2[3-5]和多调和算子Δn[6-7]的离散谱问题进行了全面深入的研究，并推广讨论了一些由Δ构成的算子组的谱问题[8-9]，得到了相应问题谱的近似值或估计不等式，他们更感兴趣的是推出不受区域度量限制的谱的万有不等式。最近，笔者在文献[8]中讨论了如下一类偏微分算子组的谱问题：

(1)

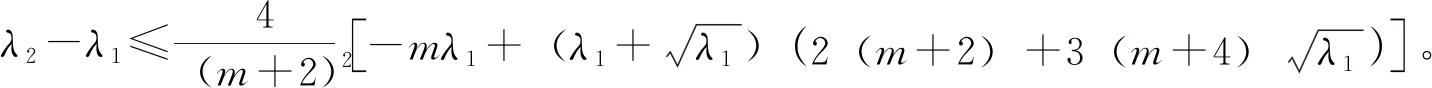
(2)

将问题(1)中的方程个数和左右算子阶数进行推广，讨论问题(1)的一般情形，即下列多调和算子组的广义谱问题：

(3)

其中，常数ai≥0(i=1,2,…,l)。因为相邻两谱的差具有很强的实际意义，例如在物理学中描述原子、分子等微观粒子运动状态的方程中，相邻谱的差就对应了粒子由一种能级状态跃迁到邻近另一种状态时所吸收或释放的能量。所以，对相邻两谱，尤其是前两个谱的间隙估计受到了国内外多位学者的重视[10-12]，本文也仅探讨问题(3)的主、次谱间隙的估计，运用变分原理[13]，对满足s>r≥1,l≥2的任意整数得到了估计问题(3)主次谱间隙的一个上界不等式，主要成果如下：

定理1问题(3)的主、次谱λ1和λ2的间隙有如下的万有估计①：

(4)

注①: 特别地，当s=l=2,ai=0(i=1,2),r=1时，估计结论式(4)恰好就成为了式(2)，即文献[8]中定理1的等价形式。

1 预备知识

(5)

假设问题(5)的主谱λ1对应的主特征向量为u，满足正规化条件：

(6)

这里，∇表示梯度算子，利用式(5)、分部积分、边界条件和式(6)，有：

(7)

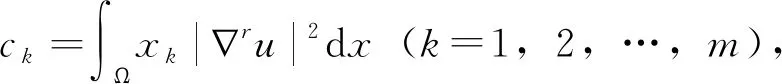
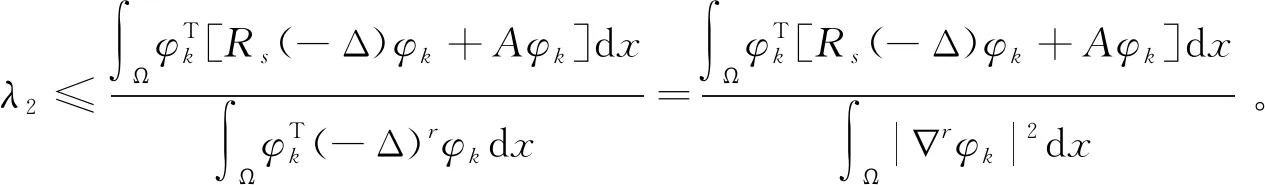
(8)

利用φk的定义、式(5)和简单的计算可得：

Rs(-Δ)φk+Aφk=(xk-ck)Rs(-Δ)u-2BRs-1(-Δ)uxk+(xk-ck)Au=xkλ1(-Δ)ru-2BRs-1(-Δ)uxk-ckλ1(-Δ)ru，

这里，B=diag[s,s+1,…,s+l-1]，再利用测试函数φk与u的广义正交性，有：

(9)

另一方面，利用分部积分，有：

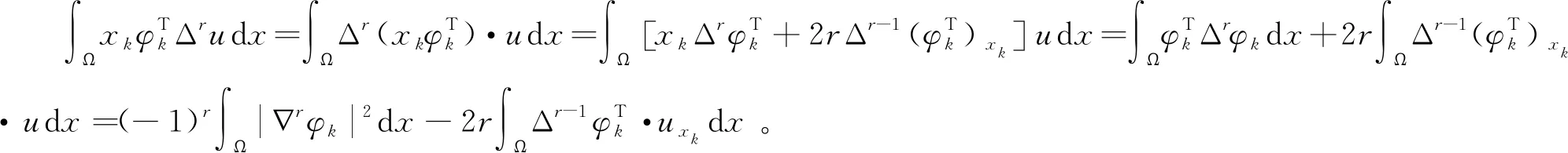
(10)

从式 (9) 和 (10)，可得 ：

(11)

2 定理的证明

引理1 设u是问题(5)对应主谱λ1的特征向量，则：

这里，C=diag[c1,c2,…,cl],ci≥0(i=1,2,…,l),j=r+1,r+2,…,s。

证明: (a) 首先，用数学归纳法证明在齐次边界条件下，方程(-Δ)s+i-1vi+aivi=λ(-Δ)rvi对应主谱λ1的特征函数vi满足下列估计式：

(12)

当ki=r+1时，由分部积分公式、Schwarz不等式和式(6)，有：

此时，式(12)成立。假设ki=r+n≤s+i-3时，式(12)成立，则当ki=r+n+1时，利用分部积分、Schwarz不等式和假设前提，有：

化简上式，得：

即ki=r+n+1时，式(12)也成立，于是式(12)得证。其次，反复运用式(12)和(7)，有：

(13)

于是：

引理1(a)得证。

(b)利用式(6)、分部积分、Schwarz不等式和(13) (其中，取ki=r+1,i=1,2,…,l)，有：

引理1(b)证毕。

引理2设u是问题(5)对应主谱λ1的特征向量，则：

(j=1,2,…,s-1)

证明: (a) 利用分部积分和Δ的定义，有：

上述D=diag[c1,-c2,…,(-1)l-1cl]，于是引理2(a)得证。

(b)类似地，

引理2(b)得证。

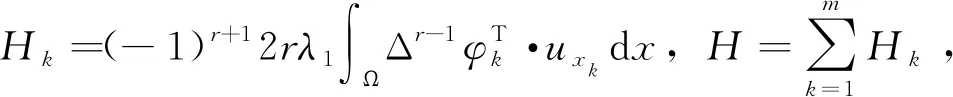
证明: 运用分部积分，有：

移项得：

于是，根据引理1(b) ，有：

引理3得证。

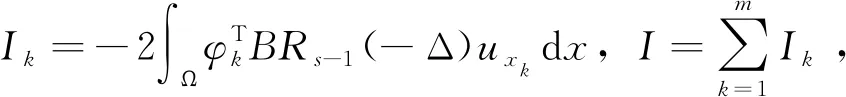
证明: 运用分部积分，有：

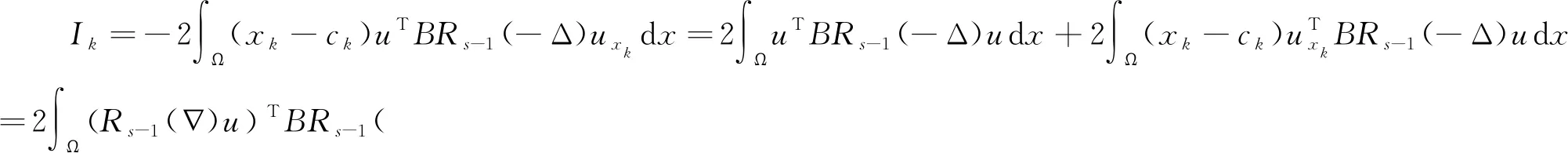
这里F=diag[s-1,s,…,s+l-2]，上式移项后，有：

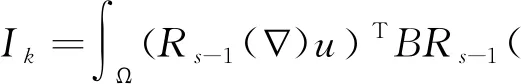
利用引理2(a)和引理1(a)，有：

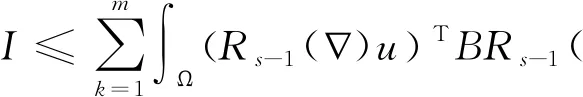
引理4成立。

引理5 测试函数φk和主谱λ1满足下列不等式：

证明: 利用φk的定义和分部积分，有：

上式移项求和，并利用引理2(b)和式(6)可得：

(14)

利用式(14)、Schwarz不等式、引理2(b)和式(13)，有：

(15)

根据式(14)和(15)，引理5成立。

定理1的证明: 在式(11)中将k从1到m求和，有：

将上式代入式(8)，可得：

(16)

从引理5，可得：

(17)

于是，将引理3、4中的估计结论和式(17)同时代入式(16)，化简即得定理1中的式(4)。

3 结语

自然界、工程技术中许多的复杂问题都可归结为高阶微分系统的谱问题，在有关调和算子谱估计等问题的研究基础上，推广讨论了高阶调和算子组的谱问题，借助变分原理，得到了估计主次谱间隙的一个上界不等式，结果显示，参考文献[8]中讨论的问题仅是本文问题的特殊情形，因此，本研究结论在微分算子的谱理论以及物理等学科中有着更广的应用价值。