基于深度神经网络算法的风电功率短期预测模型

朱宗玖，刁海岸

(安徽理工大学 电气与信息工程学院，安徽 淮南，232001)

2021年上半年，我国风电新增装机1 084万kW，累计装机达到2.92亿kW[1]。风电已经从补充能源逐渐变为替代能源。但风力发电受到天气因素等影响，风电输出功率不稳定，大规模风电入网还会影响电网的安全稳定。对短期风电功率进行准确预测有助于优化电网调度，保障电力系统的稳定运行。常见的风电功率预测方法可分为物理预测和统计预测，物理预测主要通过风电场附近环境条件和天气信息将风能计算成风机的动能来预测功率[2]，但该方法中很多环境条件不能被准确描述，预测误差较大。统计预测方法通过分析历史数据之间的规律建立模型，包括BP神经网络和各类神经网络等人工智能算法[3]，可以避免因环境条件描述不准确而导致的预测误差，文献[4]使用鲸鱼算法优化支持向量机对风电功率进行预测，但没有考虑时间序列对风电功率的影响，预测精度较低。随着深度学习模型的发展[5]，卷积神经网络(convolutional neural network，CNN)和循环神经网络(recurrent neural network，RNN)[6]在风电预测中取得了良好的效果，深度学习模型较于传统物理预测方法和统计预测方法，它有更好的预测效果。文献[7]建立长短期记忆网络(long-short term memory，LSTM)对风电功率进行了超短期预测，解决了使用RNN预测易丢失长时记忆信息等缺点，但预测精度还有待提高。文献[8]使用门控循环单元(gated recursive unit，GRU)对风电功率进行预测，GRU不仅结构简单，还提高了预测效果，但未考虑到数据维度过高难以建立预测模型的情况。

因此，本文结合CNN和GRU算法，提取历史数据的时间序列特征，对风电功率进行短期预测。使用主成分分析(principal component analysis，PCA)法减少风电功率数据维数，再使用CNN对降维后数据序列进行特征提取，对历史风电功率数据进行训练，从而建立GRU网络模型。最后，通过黑龙江某风电场实测数据进行仿真分析，并将该结果与GRU和CNN的结果对比。

1 数据分析降维

1.1 主成分分析(PCA)

建立预测模型，首先，需要找到影响风电功率的因素，获取风电功率历史值和同一时刻影响风电功率的风速、风向、温度等6种时间序列数据。由于数据维数过多，会造成模型中的数据冗余，在参与模型预测前须先使用主成分分析法对数据进行降维。

主成分分析可以将风电功率多维数据分解成可以代替原始数据的低维数据集，提取到对模型预测最有用的特征值。假设原始风电功率数据矩阵A={X1,X2,…,Xm}(数据的维数为m)，先进行中心化:

(1)

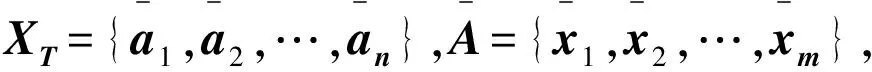
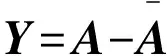
(2)

求得协方差矩阵为

C=YTY

(3)

求得C的m个特征向量按大小顺序组成矩阵W，只取W的前l列求降维矩阵：

Tl=YWl

(4)

这样就得到了低维的风电功率数据矩阵，能够有效降低后续模型的计算量，并且有助于模型的特征提取和建模分析。

1.2 分析结果

模型输入数据为风电功率、风速、风向、气温、气压和轮毂高度空气密度6项一维时间序列，数据矩阵的n为样本的个数，m为6。

将数据进行主成分分析(表1)，可以发现，前3个主成分对风力发电功率的影响最大，贡献率近93%，因此，采用前3个主成分对数据进行高度概括。

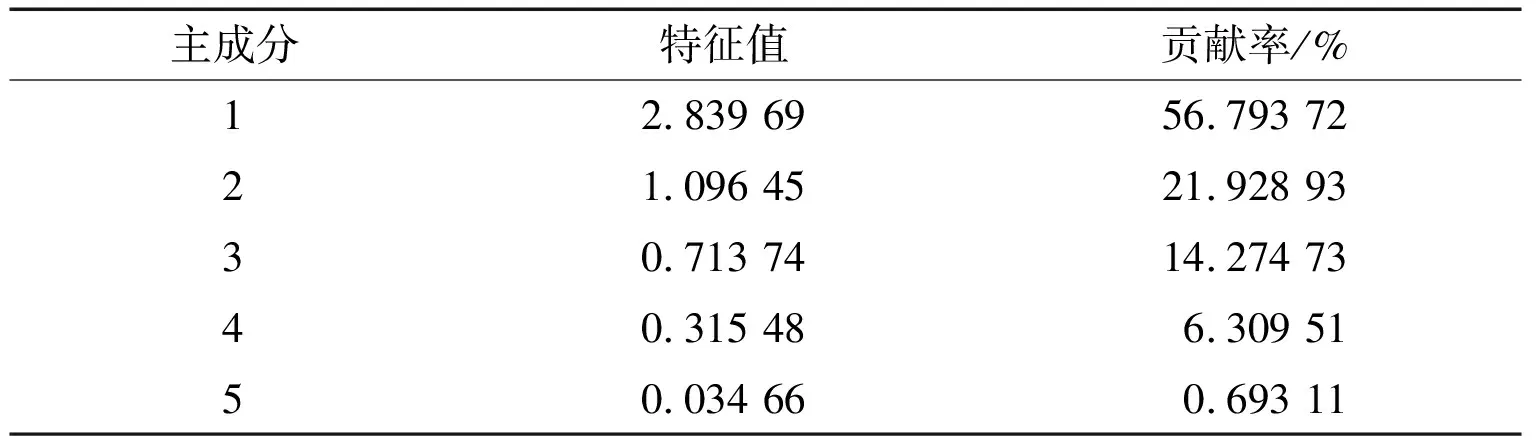
表1 风力发电功率主成分贡献表

2 CNN-GRU风电功率预测模型

2.1 卷积神经网络(CNN)

CNN是一种可以很好地处理高维数据的人工神经网络。它通常应用于视觉图像、视频识别和文本分类中。降维后的风电功率数据依然包含多维信息，为了完整描述风电数据，提出时空矩阵，时空矩阵数据基于降维后的风电场环境信息和时间序列，时空矩阵X显示为

(5)

其中，k代表第k维信息；n为随时间序列的样本个数；Xk(n)代表第k维信息在n时刻记录的数据。为了在时空矩阵中提取风电功率信息，使用CNN对时空矩阵进行处理，CNN的结构见图1。首先，卷积神经网络将许多二维时空矩阵堆叠成三维矩阵块。然后，对这些块进行卷积运算。卷积运算可以得到一个高度抽象的特征，在卷积操作之后，卷积操作的输出使用池化操作。池化操作不会使输入矩阵的深度发生变化，但可以减少矩阵的大小和节点的数量，从而减少整个神经网络中的参数。经过反复的卷积和池化操作，得到高度抽象的特征，并展平为一维向量，因此，可以与全连接层连接。可以迭代计算全连接层的权重和偏置参数。最后，通过激活函数的输出得到预测结果。

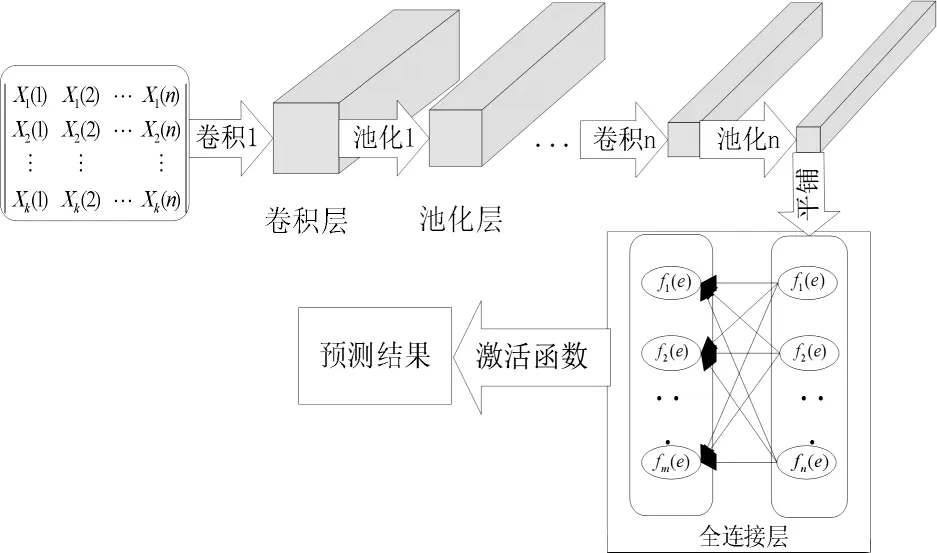
图1 CNN结构

2.2 门控循环单元(GRU)

门控循环单元(GRU)优化了循环神经网络(RNN)和长短期记忆网络(LSTM)，改进了RNN对历史值的长期依赖，同时对LSTM的结构进行了优化，使用一个更新门代替了LSTM中的记忆门和遗忘门。

GRU基本单元的内部结构见图2。其中，⊙为矩阵元素相乘；⨁表示矩阵相加；xt为当前节点输入；yt为当前隐藏节点的输出；ht-1为上一节点传递的状态；ht为传递给下一节点的状态。

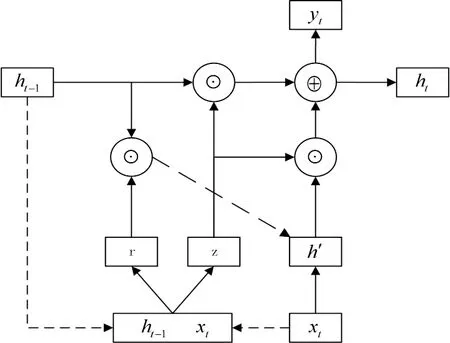
图2 GRU基本单元内部结构

提出超短期风电功率预测模型，需要基于历史风电功率时间序列来预测未来时刻的风电功率，网络结构中已经包含历史风电功率的特征，当输入风电功率xt，将和上一节点传下来的状态ht-1一起进入网络进行运算，其中，ht-1包含了之前网络中的信息。首先，在网络中使用重置门r重置上一时刻状态ht-1，计算式为

(6)

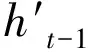
(7)

h′包含了当前输入xt信息及上一时刻信息。第三，使用更新门z对包含的隐藏状态中不重要的信息进行遗忘，对当前节点信息进行记忆，计算式为

ht=(1-z)⊙ht-1+z⊙h′

(8)

得到当前的状态ht将输出到下一个节点进行计算，从而得到准确的预测输出。

2.3 CNN-GRU混合模型

结合GRU模块能够较好地处理时序数据和CNN模块适合处理矩阵数据的优点，提出了CNN-GRU混合神经网络，见图3。

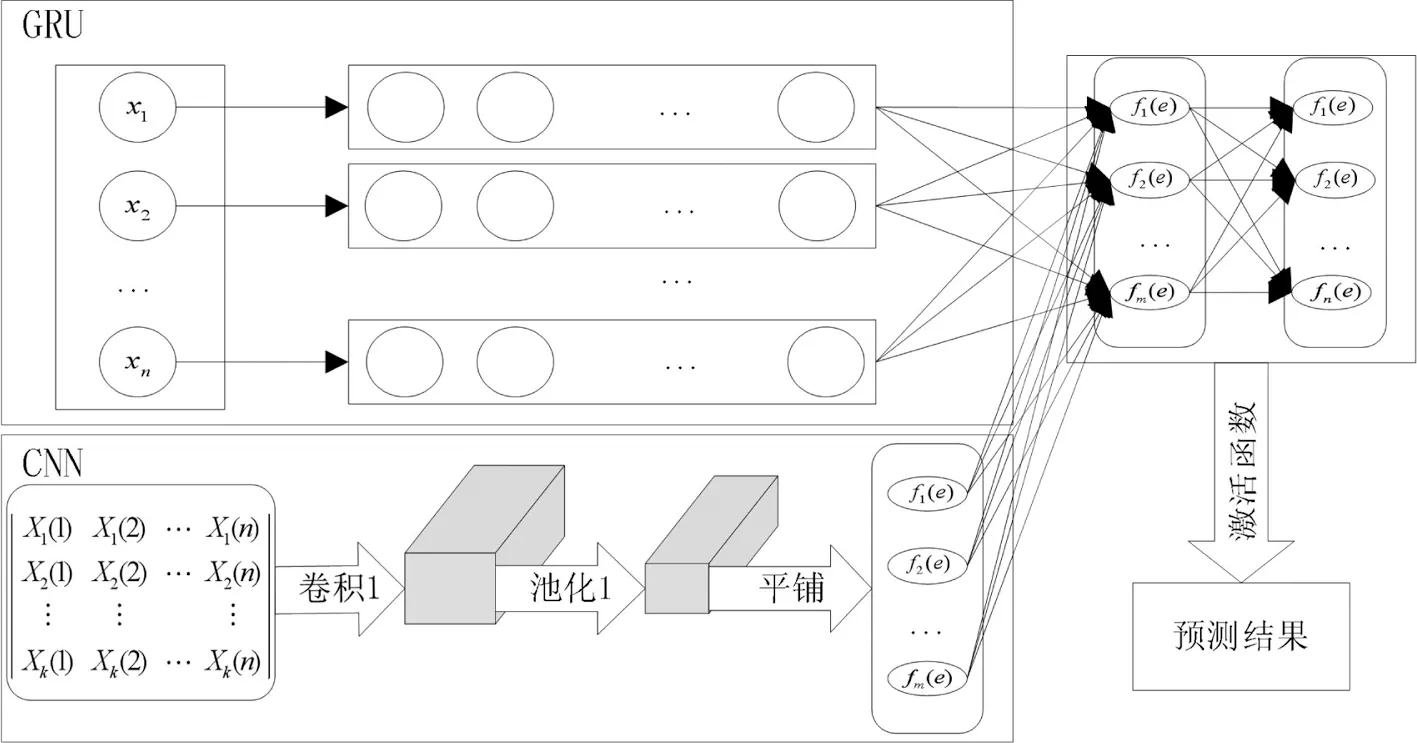
图3 CNN-GRU混合神经网络模型

所提出的CNN-GRU混合神经网络由1个GRU模型和1个CNN模型组成。输入是降维的风电功率数据；输出是对未来风电功率的预测。由于CNN模型擅长处理时空矩阵、图像等二维数据。本文的CNN模块输入的是一段时间的风电功率的时空特征矩阵，使用局部连接和共享权重直接从时空矩阵数据中提取局部特征，并通过卷积层和池化层获得有效表示。CNN的结构包括2个卷积层和1个平铺操作，每个卷积层包含1个卷积操作和1个池化操作。第2次池化操作后，将高维数据展平为一维数据，CNN模块的输出与全连接层相连。

GRU模块的目的是捕捉长期依赖关系。GRU模块可以通过记忆单元长期学习风电功率历史数据中的有效信息，而遗忘门过滤掉无效信息。GRU模块的输入是一段时间的风电功率的时序数据；GRU 模块包含许多门控循环单元，所有这些门控循环单元的输出都与全连接层相连。通过计算全连接层中所有神经元的平均值，可以得到风电功率预测结果。CNN-GRU方法流程图见图4。

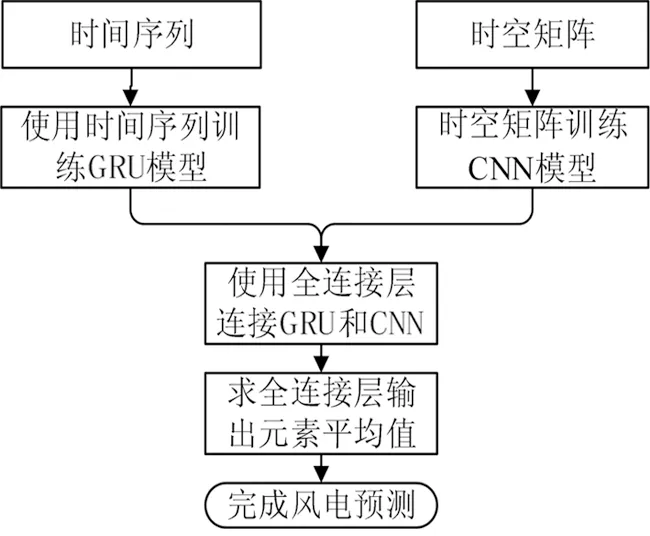
图4 CNN-GRU模型预测流程图

3 算例验证分析

3.1 算例设置

根据1.2节得出的分析结果，模型选取数据为东北某风场2017年1个月的风电功率数据和对应时间的风速、风向和温度进行短期风电功率预测，数据采样间隔为5 min，共8 640列数据。选择24 d数据作为训练集，3 d数据作为测试集，3 d数据作为预测集，以前2 h的风电功率数据预测下一时刻的风电功率。

实验基于Windows10操作系统，软件采用MATLAB2020b，CPU为InterI5-8400，GPU为GTX1060，使用GPU进行训练测试。

3.2 模型评价指标

选用平均绝对误差MAE、相对误差MAPE和均方根误差RMSE分别对本模型和其他传统模型进行比较[9]，计算公式为

(9)

(10)

(11)

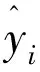
3.3 实验结果分析

为了评估 CNN-GRU 模型的性能和稳定性，选择了几个最常用的神经网络作为对比模型，包括卷积神经网络(CNN)模型和门控循环单元(GRU)模型。通过学习训练数据集获得GRU、CNN和CNN-GRU模型的参数，并将测试数据集馈送到3个预测模型。评估预测模型是否经过良好训练和学习的参数是损失函数的损失值。交叉熵函数被选为损失函数，它表征了2个概率分布之间的距离。交叉熵越小，2个概率分布越接近。交叉熵L公式如下：

(12)

其中,n是训练样本数量。损失值越接近零，预测模型越适合训练集。3种风电预测模型的损耗值见图5。

从图5可以看出，GRU和CNN-GRU模型收敛速度很快，经过 200 次迭代，它们的损失值均低于0.05，但 CNN 模型在第200次迭代时损失值仍为0.03，且CNN模型有轻微波动。所有方法在 500 次迭代后都达到了较小的损失值，这意味着所有方法都可以较好地学习训练集并在测试集上取得良好的性能。可以发现，训练集超过 500 次迭代，损失值下降得极其缓慢。如果继续增加迭代次数，所有模型在测试集上虽然表现良好，但不能对预测集进行准确预测，很明显500次后模型过拟合，所以，本次实验的迭代次数定为500次。

对GRU、CNN和CNN-GRU模型3 d风电功率预测训练，在表 2中分别给出了3个模型的负荷预测结果的MAPE和RMSE。从表2可以看出，CNN模型的3个评价标准比GRU模型低得多。由于本文的数据集大部分是时空矩阵数据，将时空矩阵数据展平为一维时间序列数据会存在一定的信息损失，因此，GRU模型无法充分学习训练集信息。而CNN擅长处理高维数据，并且可以充分快速地处理时空矩阵。提出的CNN-GRU模型是GRU模型和CNN模型的融合，提供了最好的预测结果。CNN-GRU模型的RMSE指标是所有模型中最小的。CNN-GRU模型可以较好地学习时间序列数据和时空矩阵，并从数据集中提取更多特征。CNN-GRU模型的MAPE和RMSE的平均值分别为1.443 5%和0.254 5。提出的CNN-GRU模型相对于CNN模型,均方根误差减少了17%，相对于GRU模型，均方根误差减少了41%。

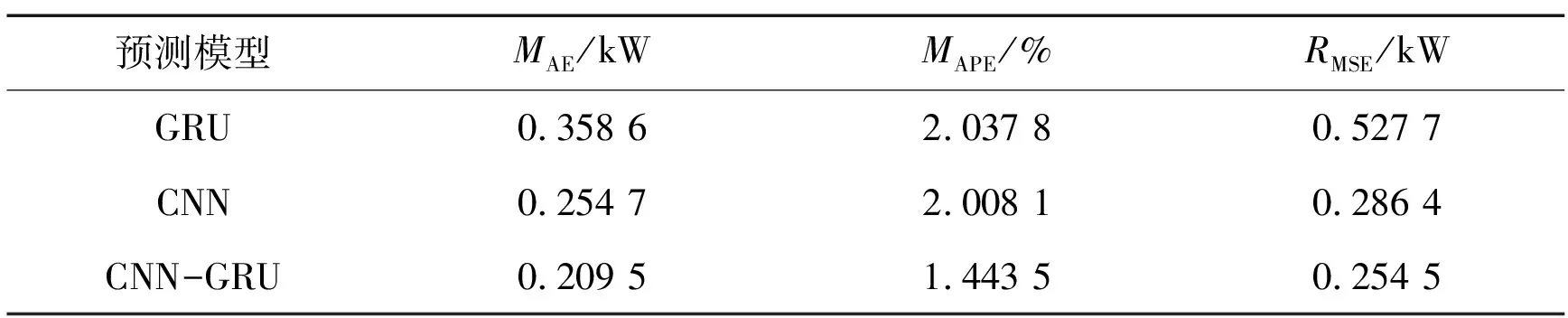
表2 CNN-GRU与传统算法的性能比较

所提出的 CNN-GRU 模型的各项评价指标值都很低，这表明，所提出的 CNN-GRU 模型在4个模型中实现了最好的预测性能。此外，预测集作为所有3个模型的输入，被发送到4个训练好的模型以预测实际风电功率。最后，得到3种模型的预测结果，并与实际风电功率进行对比，结果见图6，3种模型的预测曲线均拟合良好，无论是在波峰还是波谷，2条线几乎重叠。由于风电功率变化范围大，很难看到预测结果的细节，因此,将4种模型的相对误差分别绘制，见图7。

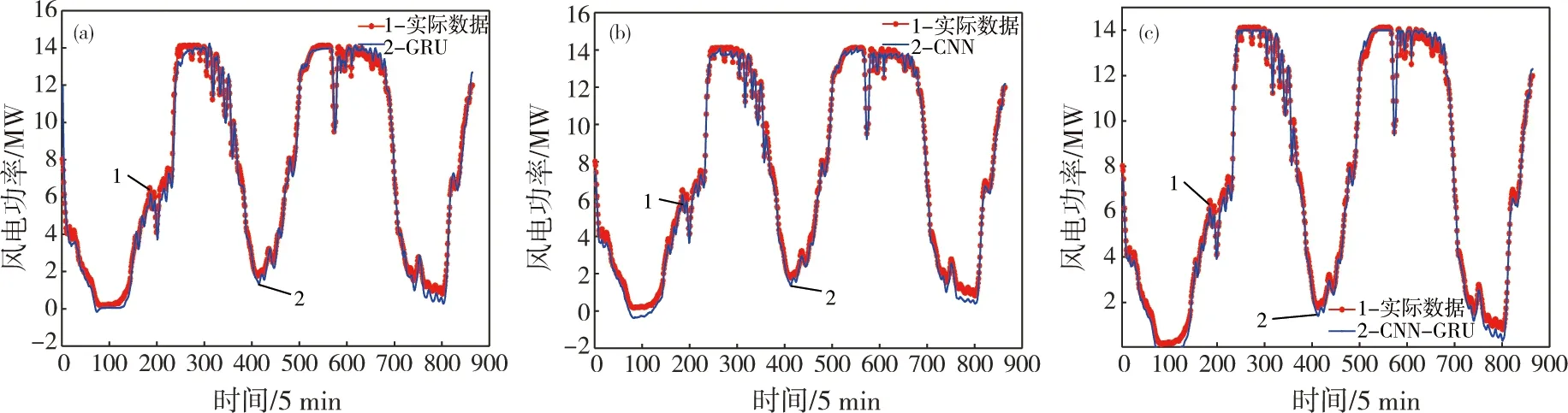
(a)GRU；(b)CNN；(c)CNN-GRU

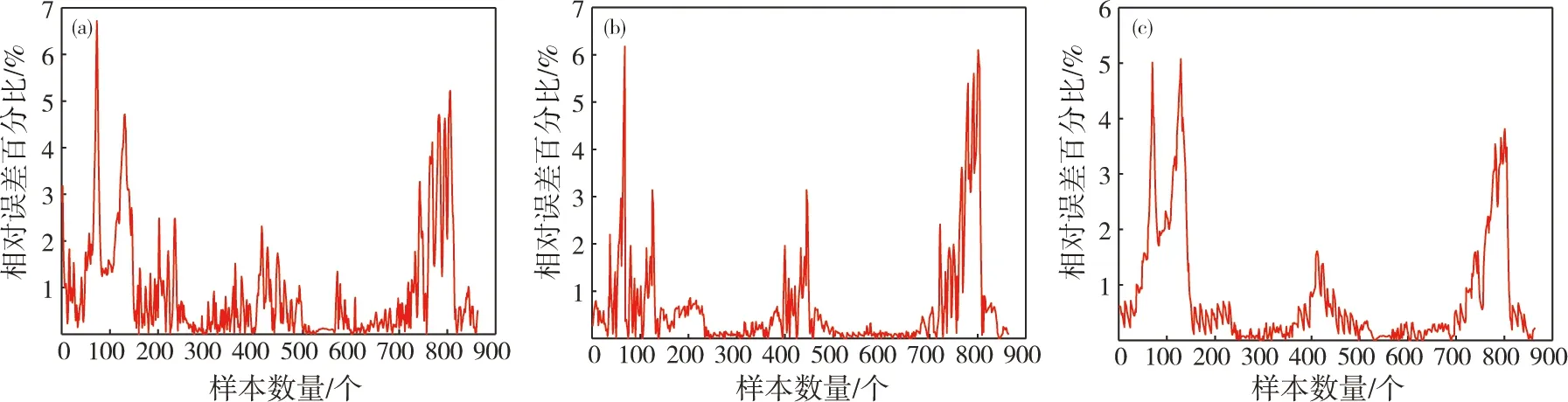
(a)GRU；(b)CNN；(c)CNN-GRU

从图7(b)可以看出，GRU的相对误差百分比波动最大，从0到7%波动，GRU预测模型的最大相对误差百分比为6.719%，MAPE为2.037 8%。从图7(c)可以看出，CNN-GRU模型的相对误差百分比从0到5%,波动最小，CNN-GRU预测模型的最大相对误差百分比为5.074%，MAPE为1.443 5%。CNN模型的最大相对误差百分比为6.175 98%，MAPE为2.008 1%。从预测集的实验来看，所提出的CNN-GRU模型实现了最准确和稳定的预测结果。将3个模型和实际数据的所有风电功率预测结果和实际风电功率绘制，见图8。

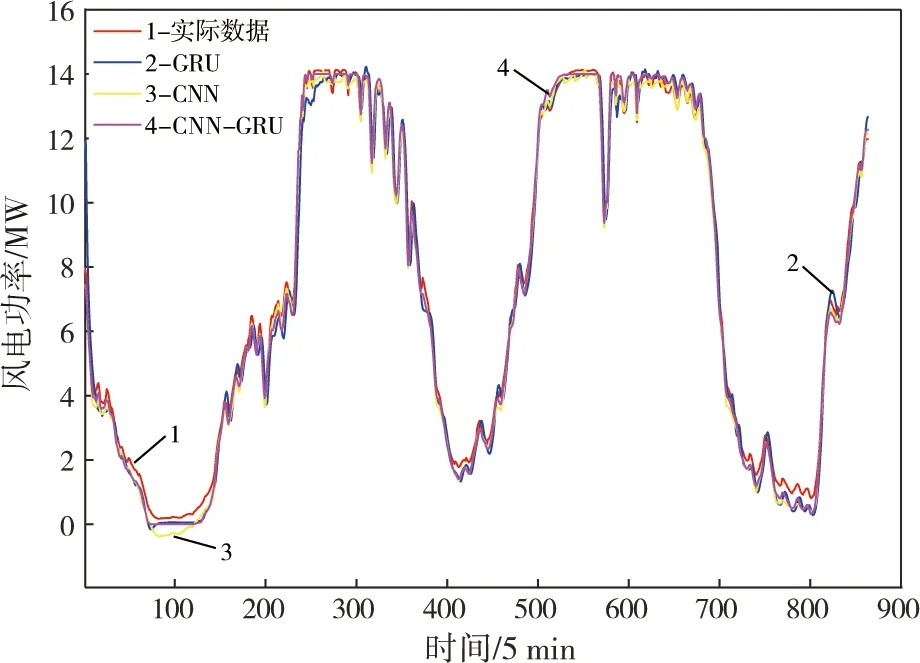
图8 不同预测模型的结果与实际数据的对比

在图 8中，3个模型都可以在预测集上进行准确预测，提出的 CNN-GRU 预测方法最适合。GRU、CNN模型无法准确分析风电功率波动规律，导致预测精度下降。相比之下，CNN-GRU 模型可以有效学习风电功率变化趋势，准确分析到达峰值期间输入特性对风电功率的影响，保证了预测精度。

4 结语

1)为了提高风电功率预测的准确率，提出了基于GRU模型和CNN模型的CNN-GRU风电功率预测模型。模型可以从影响风电场风电功率的可变数据中提取特征来快速准确地预测风电功率。

2)在黑龙江某风电场预测的实际实验中，将提出的CNN-GRU模型与GRU和CNN模型进行了比较。仿真结果表明，本文的算法模型可以较好地处理时间序列数据和时空矩阵数据，并且可以有效地提取数据集的隐藏特征。所预测的结果MAPE和RMSE最低，相比CNN模型,均方根误差减少了17%，相比GRU模型，均方根误差减少了41%。