基于TOPSIS和灰色关联度的电网企业运营项目风险衡量模型

丁智华， 黄鑫， 林可尧

(国网福建省电力有限公司，福建，福州 350001)

0 引言

电网企业越来越重视运营项目风险衡量工作，通过风险衡量结果找出潜在风险，为企业升级与转型提供更加可靠的发展战略[1]。因此，文献[2]提出了一个基于rSYR指标的风险衡量模型，结合企业运营项目存在的问题，分析这些问题在项目中的风险贡献度，同时为了避免项目规模效应，还对该指标进行了标准化处理，加强模型的衡量效果。文献[3]基于稳健极端值模型，刻画企业的项目风险类别，优化风险衡量模型。

但是以上方法的风险衡量模型的衡量步骤相对单一，无法对风险类型进行细分，由此，引入TOPSIS和灰色关联度方法，对电网企业运营项目风险衡量模型的构建过程进行详细描述。其中，灰色关联度是对象变化关联的度量结果；TOPSIS是technique for order preference by similarity to ideal solution的简称，译成中文为逼近理想解的排序方法，该方法通过计算有限的评价指标与理想解，对评价数据进行最优排序。

1 电网企业运营项目风险衡量模型

1.1 度量电网企业运营项目风险元

风险指标是实际结果与预期结果之间的衡量指标，因此建立衡量模型，需要将风险作为衡量指标[4]，此时，为了使构建的模型能够有效衡量运营项目风险，引入风险元的基本内涵，并度量电网企业运营项目风险元。

现阶段，电网企业运营项目风险元即运营项目中存在的主要问题包括：项目立项时，可行性报告编制质量不高，缺乏深度，导致项目范围不清、清单不实、概算不实；需求报送，物资或服务供应商报送不及时、不准确，且不确定材料影响实施进度；过程管控方面，施工管理单位落实协调、跟踪等管理职责不到位，项目节点经济核算不一致，成本信息不对称，技术方案不落实，经常变更或签证导致预算失控；验收收尾中存在一些隐蔽环节，验收不够详细，甚至计划少，容易出现廉政风险。

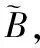
(1)

模糊风险元的度量公式为

(2)

式中,G表示归一化常数,W(fi)表示论域W中，映射范围fi为[0,1]的模糊函数。灰色风险元的度量公式为

(3)

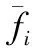
(4)

1.2 基于TOPSIS和灰色关联度设置风险衡量

根据TOPSIS和灰色关联度基本定义，设置模型衡量电网企业运营项目风险衡量的一般步骤。规范风险指标，利用熵权法确定风险指标的权重，以此构建指标矩阵：

(5)

对4个风险元指标进行评价，对应的指标统一用uij表示。鉴于风险元指标之间的差异性较大，因此规范化处理上述公式，得到无量纲化指标矩阵：

(6)

熵权法确定风险指标权重，第j个指标的熵值为

(7)

式中,hi表示熵值,gij表示第j类风险元中第i种方案的比重。因此根据上述计算，得到第j个指标的熵权为qj，指标权重为qi[8]。在整个项目的执行过程中，包括供货与设备提供进度、规范文件编制、厂家收资、交付施工阅纸进度等都属于关键点，此类细微之处也存在难点，因此，需要将指标权重规范化即与规范化的矩阵相乘，在每一个环节保证项目的执行力，得到加权标准化矩阵C，然后根据正理想解和负理想解，确定样本数据的欧氏距离和灰色关联度。下列公式为理想解的计算结果：

(8)

(9)

根据上述计算结果，得到正理想解和负理想解之间的灰色关联度[9]。其中两个理想解的灰色关联系数，计算公式为

(10)

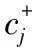
(11)

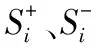
(12)

依据贴近度Ti对风险元指标进行排序，Ti值越大说明样本越贴近正理想样本,越小则越贴近负理想样本。通过TOPSIS和灰色关联度，设置模型衡量步骤。

1.3 构建风险衡量模型

根据风险元度量结果可知，目前的风险虽然主要分为4个大类，但从企业自身的角度来说，运营项目风险指标可以分为内部风险和外部风险。表1介绍了目前几种常见的风险因素[11]。

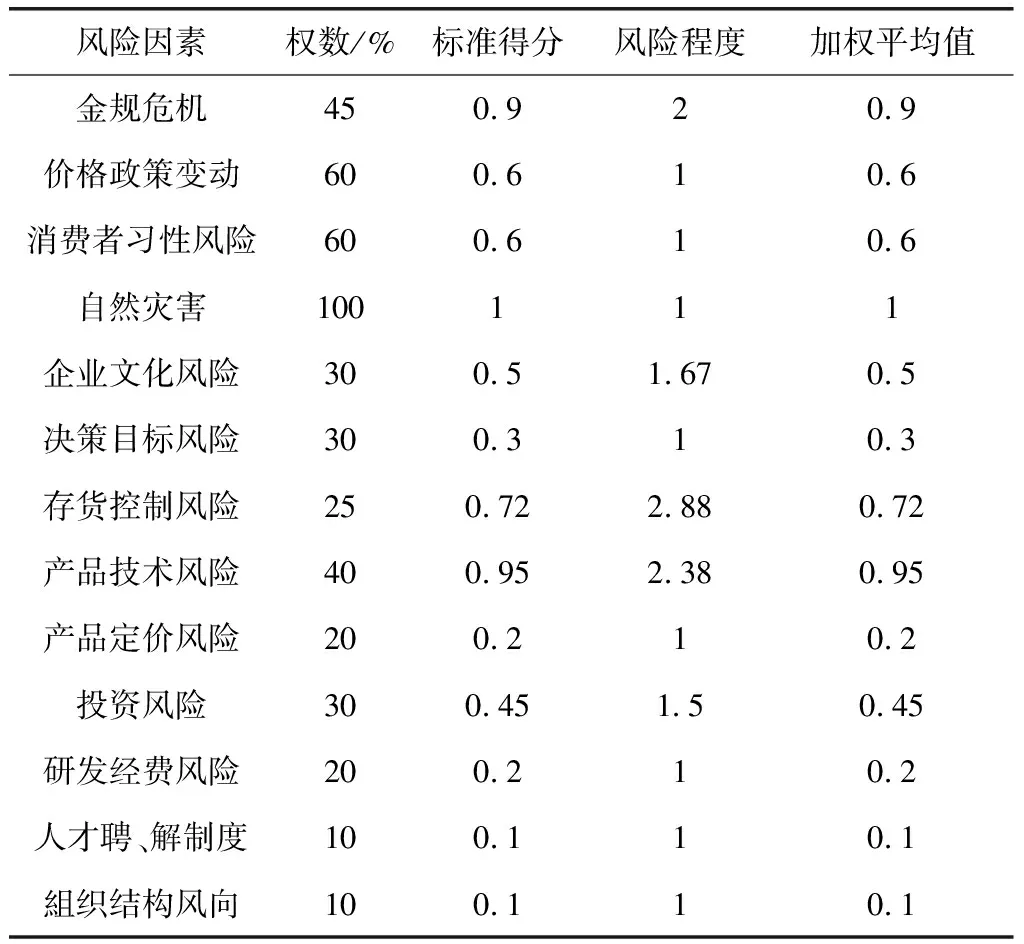
表1 常见的企业运营项目风险因素

表1中风险程度的数值，是权数与标准得分之间的比值。根据表1中的多项企业运营项目风险因素，结合基于TOPSIS和灰色关联度的风险衡量步骤，建立风险衡量模型，该模型具有二维属性，如图1所示。

图1 模型的二维属性示意图

根据图1中的数据可知:横坐标表示模型满足衡量预期和不满足预期，其中原点左侧为不满足区间，右侧为满足区间；纵坐标表示风险指标衡量结果的真实程度，其中上部表示衡量结果可信，下部表示衡量结果不可信。将度量的指标和设置的衡量步骤，与设计的模型衡量结构之间建立连接，至此在TOPSIS和灰色关联度的应用下[12]，建立电网企业运营项目风险衡量模型。

2 仿真实验

以某电力公司提出的工程进度计划与其合同草案为数据来源，以中标后签订的中标通知书和合同为准则，以安全建设协议和廉政协议声明为基础，对工程施工进度、安全控制、质量保证、合理造价等全过程进行控制，从而使变电站电网企业项目的存在和实施具有一定的权威性和普遍价值意义，可以应用到本次仿真实验当中。

将此次设计的风险衡量模型作为实验组，以文献[2]方法(传统模型1)和文献[3]方法(传统模型2)作为对照组，根据建立的仿真测试平台，对比分析本文方法风险指标衡量效果。

2.1 构造加权标准化矩阵

此次设计模型过程中，根据风险元度量结果，计算风险指标权重。下列公式是根据式(7)得到的加权标准化矩阵C的计算结果：

(13)

根据上述计算结果，按照式(8)得到同一属性指标的正理想解和负理想解；然后根据式(9)计算理想解的欧氏距离；最后根据式(10)，得到正理想解和负理想解的灰色关联度系数，从而获得灰色关联度。在上述计算分析基础上，无量纲化处理欧氏距离和灰色关联度，利用式(11)计算正理想解和负理想解的接近程度，最后根据式(12)计算相对贴近度，对风险指标进行排序优选。实验组完成上述步骤后建立风险衡量模型。为了保证此次设计的模型可以投入实验测试，设置了5类分辨系数，评价加权标准化矩阵的熵权二级指标，结果如图2所示。

图2 二级指标价值评估结果

根据图2中的测试结果可知，依据式(13)，对风险元指标进行排序，贴近度越大越说明样本越贴近正理想样本,越小则越贴近负理想样本，其中:从可靠性方面来看，E组的二级指标评估值最优；从经济性角度来看，同样是E组的二级指标评估值最优；从技术监督的角度来看，D组的评估值最优；从运行小指标来看，E组有更好的评估结果。综合上述测试结果，将分辨系数φ的值设置为与E组一致的值。其他两种传统方法也按照自身的设计步骤，建设衡量矩阵。比较3个不同的风险衡量模型，获取电网企业运营项目风险的衡量效果。

2.2 风险衡量效果测试

利用设置好的仿真测试平台模拟多组电网企业运营项目风险指标，以文中设计模型为实验组，图3为仿真结果以及3个测试组对风险指标的衡量结果。

(a)文中设计模型

根据图3可知，此次设计的模型，其风险指标衡量结果与仿真测试平台的仿真数据高度近似，最高可达0.59，相似度最高为98%，而两个传统模型的风险衡量结果却与仿真数据之间存在较大差异，可见此次设计的模型衡量风险的能力更强。

2.3 风险类型识别效果测试

保持基本测试条件不变，利用3个测试组，识别仿真空间中虚拟的风险数据，并对风险类型进行定位区分。测试结果如图4所示。

(a)文中设计模型

图4中，此次设计的模型将风险类型进行准确分类，而两个传统模型的风险分类效果并不理想，因此其风险程度衡量结果，可能会偏离仿真数据，贴近负理想样本。可见TOPSIS和灰色关联度应用下，本文设计模型的识别能力得到提升。

3 总结

在参考传统设计方法的基础上，将TOPSIS和灰色关联度方法与衡量模型相结合，实现了模型整体性能的优化。但根据此次设计过程可知，由于TOPSIS和灰色关联度方法的计算步骤较为复杂，因此在设置模型的衡量步骤时操作较为困难，很容易出现计算错误的情况。因此今后的研究任务中，可以对TOPSIS和灰色关联度方法进行计算步骤优化，使整个设计过程更加简洁便利，提高整体工作效率。