Hyperparameter on-line learning of stochastic resonance based threshold networks

Weijin Li(李伟进), Yuhao Ren(任昱昊), and Fabing Duan(段法兵)

College of Automation,Qingdao University,Qingdao 266071,China

Keywords: noise injection,adaptive stochastic resonance,threshold neural network,hyperparameter learning

1. Introduction

Gradient-based optimizers are commonly used for training neural networks,but a necessary condition for successfully implementing the network performance optimization is the continuously differentiable activation functions therein. However,the introduction of the piecewise-linear(e.g.,ReLU)[1,2]or the hard-limited (e.g., binarization) activations[3,4]has gained increasing attention in recent years due to the fact of training much deeper networks or largely saving memory storage and computation.[1–8]Therefore, training the neural network with nondifferentiable or zero-gradient activation functions becomes a tricky problem for applications of available gradient-based optimizers.

A natural way of training threshold neural networks by the gradient-descent based back-propagation algorithm is approximating the nondifferentiable threshold neuron to a smoothed activation function,[6,9–13]but performing the network testing with threshold activation functions and the well trained network weights. For instance,a conventional method is to substitute the sigmoid function 1/(1+e−λu)with a large parameterλ>0(e.g.,λ=10)for the threshold neuron.[9–11]Unfortunately, the generalization performance of the threshold neural network is unsatisfactory in testing phase,because network weights are inadequately trained for the saturated regimes of the sigmoid function.[6,9–13]

Recently, the approach of noise injection becomes a useful alternative option to optimize the artificial neural network.[4,6,8,12–22]It is interesting to notice that the benefits of injecting noise in threshold neural networks can be viewed as a type of stochastic resonance effect,[22]because there is also a nonzero noise level for improving the performance of nonlinear systems.[6,12–14,23–33]By injecting artificial noise into the saturated regime of activation function[4]or smoothing the input-output characteristic of hard-limiting neurons with an ensemble of mutually independent noise components,[6,12,13]the non-differentiable threshold networks own a proper definition of the gradients. Then, the gradientbased back-propagation algorithm can successfully perform in finely transformed threshold neural networks. Meanwhile, a stochastic resonance based threshold neural network on the distribution of injected noise into the hidden layer is proposed for effectively recycling the back-propagation training algorithm.[6,12,13]Furthermore,using a stochastic gradient descent (SGD) optimizer, we actually realize a noise-boosted back-propagation training algorithm in this kind of stochastic resonance based threshold networks by adaptively learning of both weights and noise levels.[13,29]

The introduction of injected noise into the threshold neural network extends the order of dimension of the parameter space, and also poses a challenge to the SGD optimizer for finding a good optima in the non-convex performance landscape of the loss function.[34–38]This is because the SGD optimizer is sometimes trapped in a domain of the flat landscape of the loss function,and the gradients with respect to the noise level and network weights approach zero.[36–38]In this paper,the noise-boosted Adam optimizer is further demonstrated to train the stochastic resonance based threshold neural network more effectively in comparison with the SGD optimizer. It is shown that,with the powerful hyperparameter on-line learning capacity of the Adam optimizer,[34–38]the designed threshold network can attain the much lower mean square error (MSE)for function approximation or the higher accuracy for image classification. Moreover, in the testing phase of the stochastic resonance based threshold neural network,the practical realization of the threshold network trained by the Adam optimizer requires less computational cost than that of the optimized threshold network by the SGD optimizer. The benefits of injected noise manifested by the Adam optimizer in each hidden neuron with different noise levels also conduce to the research of exploiting adaptive stochastic resonance effects in machine learning.

2. Main results

2.1. Stochastic resonance based threshold network

Consider anN×K×Mfeed-forward threshold neural network with three layers.[6,12,13,29,39,40]The input layer receives the datax ∈RN×1,and the weight matrixW ∈RK×Nconnects the hidden layer and the input one. The hidden layer consists ofKthreshold neurons[41]described as

with an adjustable threshold parameterθkfork=1,2,...,K.The weight matrixU ∈RM×KconnectsKthreshold neurons in the hidden layer withMlinear activation functions in the output layer, andy ∈RM×1denotes the network output vector.

It is seen from Fig. 1(a) that the threshold activation functionψ(u) of Eq. (1) is nondifferentiable atu=θkand with zero-gradients foru ̸=θk. Based on the noise injection method,[6,12,13,29,39,40]we can replace the activation functionψ(u) in Eq. (1) with a differentiable one. This process is formed by injecting a sufficiently large numberTof mutually independent noise variablesηtwith the common probability density function (PDF)fη(η), as shown in Fig. 1(b). Then,a continuously differentiable activation function is deduced as the substitution,i.e.,the expectation[6,12,13,29]

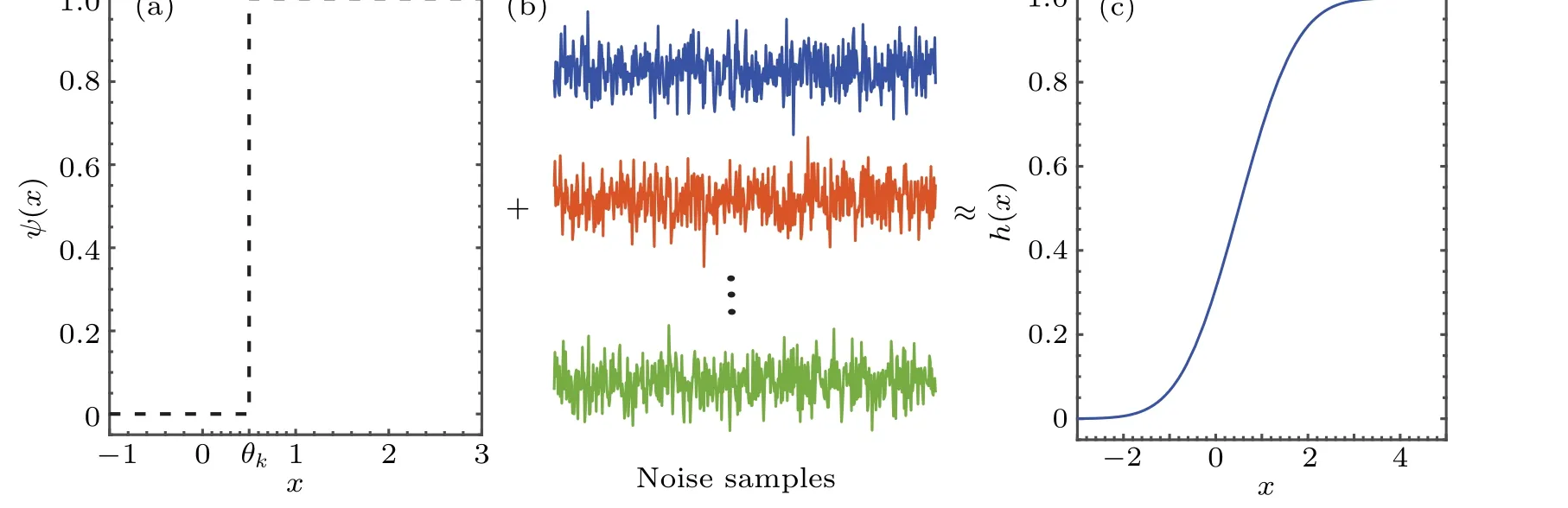
Fig.1. (a)Threshold activation function ψ(u)in Eq.(1)with the threshold parameter θk,(b)an ensemble of T noise samples with a common level σ of the standard deviation and(c)the noise-smoothed activation function h(x)with learnable parameters θk and σ.

It is interesting to note that, for the designed threshold neural network with the hidden neuron given by Eq. (2),the aforementioned difficulty of training threshold neural networks can be overcame,because the activation functionh(x)in Eq.(2)has its finely defined gradient∂h(x)/∂x=fη(θk −x).Furthermore,it is emphasized that the effective learning ability of the designed threshold neural network is also extended by the introduction of the learnable parameters of noise levelsσkand thresholdθkin Eq.(2).During the training process,the parametersσkandθk,as well as the network weight matricesWandU, are all optimized by the gradient-based learning rule. Specially, we here represent the corresponding gradients as∂h(x)/∂σk=∞θk−x ∂fη(η)/∂σkdηand∂h(x)/∂θk=

−fη(θk −x)with respect toσkandθk,respectively. Thus,the back-propagation learning algorithm can be successfully implemented for training the designed threshold neural network.

2.2. Motivated example

Let{x(ℓ),s(ℓ)}Lℓ=1denoteLexamples of the training set to train the desinged threshold network in a supervised learning manner, ands ∈ℛM×1represents the desired response vector. The loss function of the empirical mean square error(MSE)can be calculated as

where‖ · ‖denotes the Euclidean norm. LetΘ ∈{W,U,θk,σk}denote the learnable parameter of the designed threshold network,the plain stochastic gradient descent(SGD)optimizer updates the parameterΘby the learning rule

Then, the 1×K×1 (K= 10) stochastic resonance based threshold neural network is trained to fit the training set{x(ℓ),s(ℓ)}Lℓ=1sampled from the target function of Eq. (5).Here,the learning rate takesα=0.01,the initial noise levelsσk(0)=1, the initial threshold parametersθk(0) and the initial weight vectorsW(0)andU(0)are uniformly distributed in the interval [−1,1]. The learning process ofJmseof the designed threshold network is shown in Fig. 2 via the SGD optimizer for different initial values of learnable parameters.

It is important to note in Fig. 2 that the SGD optimizer is sensitive to the initial values of parameters. For example, setting the initial weightW1,1=−5 and the noise levelσ8=1, it is seen in Fig. 2 that the MSEJmse(∗) of the designed threshold network converges to a local minimum ofJmse=1.149×10−3after 5000 epochs of training. However,when the initial values ofW1,1=−2.3 andσ8=0.2 are not properly set, it is shown in Fig. 2 that the learning trajectory of the MSEJmse(▽) is stuck in a flat landscape of the network performance surface, because the gradient herein is almost zero in every direction. Here,besidesW1,1and the noise levelσ8,other parametersΘ ∈{W,U,θk,σk}are fixed.

Next, we employ the Adam optimizer to update the parameterΘof the stochastic resonance based threshold neural network by the learning rule[34]

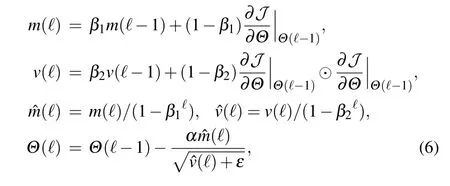
whereβ1=0.9 andβ2=0.999 are attenuation coefficients,0<ε ≪1 is the regularization parameter,m(ℓ) denotes the first-order moment with its corrected value ˆm(ℓ)andv(ℓ)is the second-order moment estimation with its corrected value ˆv(ℓ).The operator⊙denotes the Hadamard product. Likewise,starting from the initial values ofW1,1=−2.3 andσ8=0.2,it is seen in Fig. 2 that the MSEJmse(+) of the designed network trained by the Adam optimizer can escape from the flat landscape of the network performance surface,and finally converge to the minimum ofJmse=1.109×10−3.Here,other parametersΘ ∈{W,U,θk,σk}(not includingW1,1andσ8)are fixed as the converged values searched by the SGD optimizer. This result clearly shows that the Adam optimizer,compared with the SGD one, is more efficient for optimizing the designed stochastic resonance based threshold network.

Fig.2.(a)Performance surface and(b)the corresponding contour of the MSE Jmse versus the weight W1,1 and the noise level σ8 of the eighth hidden neuron. The learning curves of Jmse of the designed threshold network are also illustrated for different optimizers.

Furthermore, it is shown in Fig. 3 that the Adam optimizer can optimize the designed threshold network with a smaller MSEJmse=1.137×10−5after 1600 epochs of training.Here,the performance surface is still illustrated versus the weightW1,1and the injected noise levelσ8, but the optimum value ofJmse=1.137×10−5is searched over the the whole space of the learnable network parameters by the Adam optimizer.The parametersΘ ∈{W,U,θk,σk}includingW1,1and the noise levelσ8are simultaneously updated by the learning rule of Eq.(6).

It is emphasized that each hidden neuron in Eq.(2)is associated with one noise levelσkfork=1,2,...,K. Thus, in the training process of the designed threshold network,the injected noise will manifest its beneficial role as the convergence of the noise levelσkreaches a non-zero(local)optimum. It is seen in Figs.2 and 3 that,for a given weightW1,1nearby 1.2,the conventional stochastic resonance phenomenon can be observed as the noise levelσ8increases. When the noise levelσ8reaches the corresponding non-zero(local)optimum,the MSEJmseattains its minimum. It is noted that the resonant phenomenon of the designed threshold networks characterized by the MSEJmseis induced by a bundle ofKnoise levelσkin the hidden neurons.The stochastic resonance phenomenon shown in Fig.2 or Fig.3 only describes a slice of the MSEJmseversus the noise levelσ8for visualization. In view of the learning curves of theKnoise levelsσk,Fig.4 also presents the distinct characteristic of the adaptive stochastic resonance effect in the training phase. The learning curves of the injected noise levelsσkin Fig.4 show that the noise levelsσkstart from the same initial value of unity, and converge to different but non-zero optima. This fact also validates the practicability of the proposed noise-boosted Adam optimizer in Eq.(6)by adaptively optimizing the noise level in the training phase.

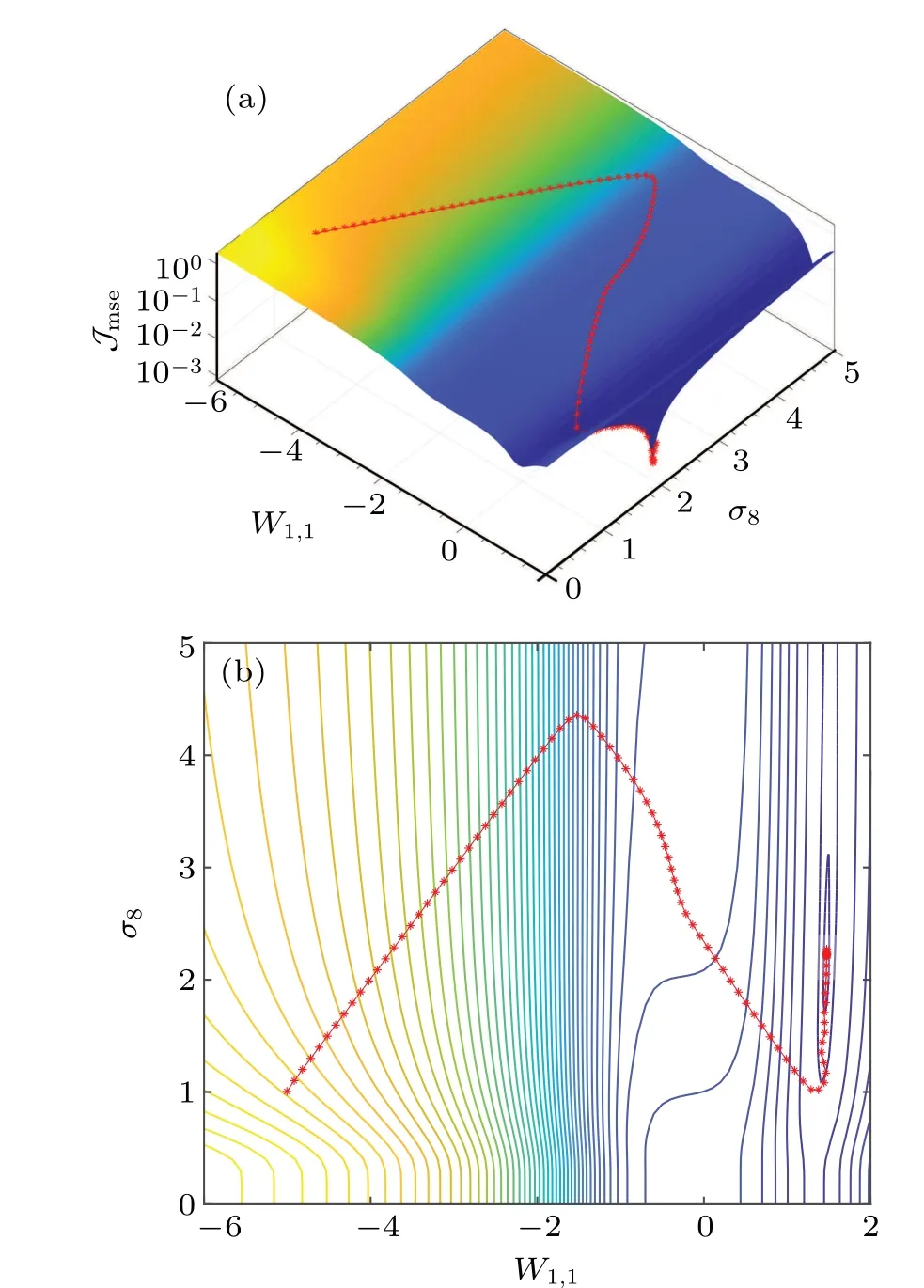
Fig. 3. (a) Performance surface and (b) the corresponding contour of the MSE Jmse versus the weight coefficient W1,1 and the noise level σ8 of the eighth hidden neuron. The learning curve(∗)of Jmse is also illustrated for the Adam optimizer.

However,the hidden neuronh(x)in Eq.(2)is a limit expression,which ensures the success of training,but cannot be realized in practical testing of the threshold neural network. In testing experiments, the hidden neuronh(x)needs to be realized as

where a finite numberTof threshold activation functions in Eq. (1) are activated byTmutually independent and identically distributed noise componentsηt, respectively. For 103testing datax(ℓ) equally spaced in the interval [−2,2], the trained threshold neural network with the hidden neuronsh(x)indicated by Eq. (7) is simulated for 102times. In each trial,for thek-th hidden neuronh(x) (k=1,2,...,K),Tindependent noise componentsηtare randomly generated at the converged noise levelσkafter the training phase. Then, the outputs of the designed threshold network are averaged as an approximation to the target function of Eq.(5).

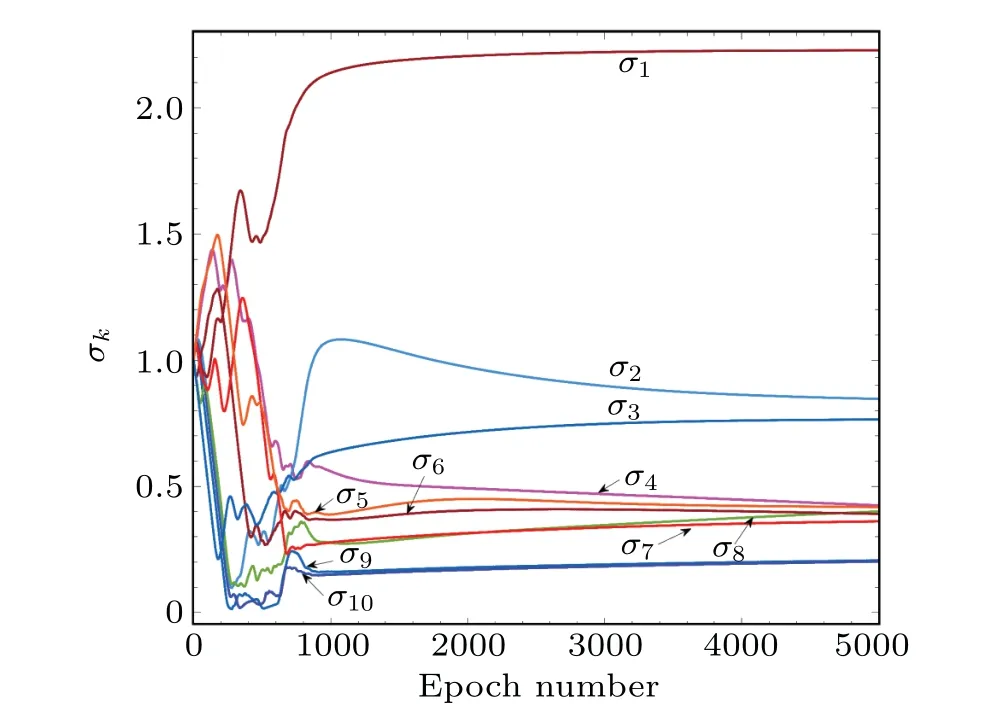
Fig. 4. Learning curves of K =10 noise levels σk in the hidden layer of the designed stochastic resonance based threshold network. Other parameters are the same as those in Fig.3.

For different numbers ofT,the experimental results of the MSEJmseare shown in Fig.5(a)for testing the trained threshold networks by both optimizers. It is seen from Fig.5(a)that,in order to achieve the same MSEJmse, the designed threshold network trained by the Adam optimizer needs a smaller numberTof threshold activation functions in Eq.(1)as well as the noise componentsηt. For instance,when the statistical mean value of the MSEJmse=4×10−4,T=3×103threshold functions in Eq. (1) are required for the designed threshold network trained by the Adam optimizer,whereasT=104threshold functions are required for the SGD optimizer. In Fig. 5(b), usingT=104threshold functions assisted by the injected noise with the same size,the output(blue dashed line)of the well trained threshold network by the Adam optimizer is plotted. For comparison,the target function(red solid line)of Eq. (5) is also illustrated. It is seen in Fig. 5(b) that the trained threshold neural network performs well on approximating the target unidimensional function in the testing phase.It is emphasized that, in the practical realization of the designed threshold network,the beneficial role of injected noise is accomplished by averaging an ensemble of threshold functions driven by the same size of injected noise samples in each hidden neuron,whereby the application of adaptive stochastic resonance in threshold neural networks is evidently confirmed.

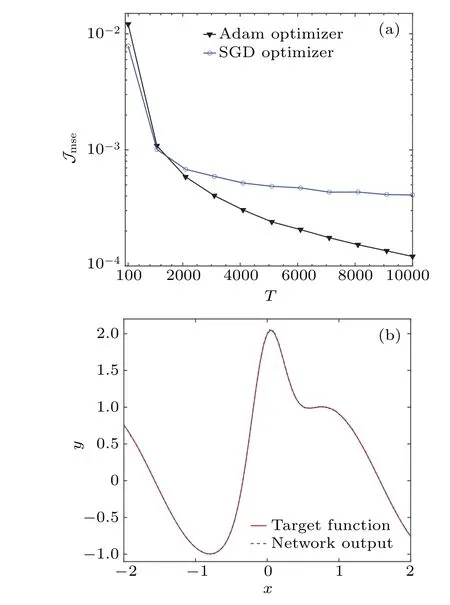
Fig.5. (a)Experimental results of the MSE Jmse for 103 testing points of the target unidimensional function in Eq.(5)versus the number T. Here,102 trials are realized for each point of experimental results,and the ensemble of outputs of T threshold functions activated by T noise samples is regarded as the realization of the hidden neuron of Eq.(7). (b)The output of the trained threshold network by the Adam optimizer as the approximation(blue dash line)of the target function of Eq.(5). For comparison,the target function(red solid line)of Eq.(5)is also plotted.

2.3. Two-dimensional function approximation

Furthermore, we consider the test of a two-dimensional benchmark function

The stochastic resonance based threshold neural network is designed with the size 2×50×1. The 16×16 training set of{x(ℓ),s(ℓ)}Lℓ=1sampled from the target function of Eq. (8) is equally spaced in the range [−3,3]×[−3,3]. After 2×104training epochs, the MSEsJmseare achieved as 0.1003 and 7×10−4for the SGD optimizer and the Adam optimizer, respectively. The Adam optimizer is still superior to the SGD optimizer in training the designed threshold network to approximate the two-dimensional function in Eq.(8).For 32×32 testing set sampled from the target function of Eq.(8)over the range[−3,3]×[−3,3],Fig.6(a)illustrates the outputs of the trained threshold network as the approximation(patched surface)of the two-dimensional functionf(x1,x2)in Eq. (8). The experimental results of the MSEJmseare obtained as 0.1012 and 7.5×10−4for the SGD optimizer and the Adam optimizer,respectively. Especially,Fig.6(b)illustrates the relative errors|y −f(x1,x2)|/∆between the outputyof the trained threshold network by the Adam optimizer and the testing data. Here, the maximum relative error is obtained as max|y −f(x1,x2)|/∆=5.188×10−3and the maximum difference∆=maxf(x1,x2)−minf(x1,x2)=13.4628 for the target function in Eq.(8)in the range[−3,3]×[−3,3].

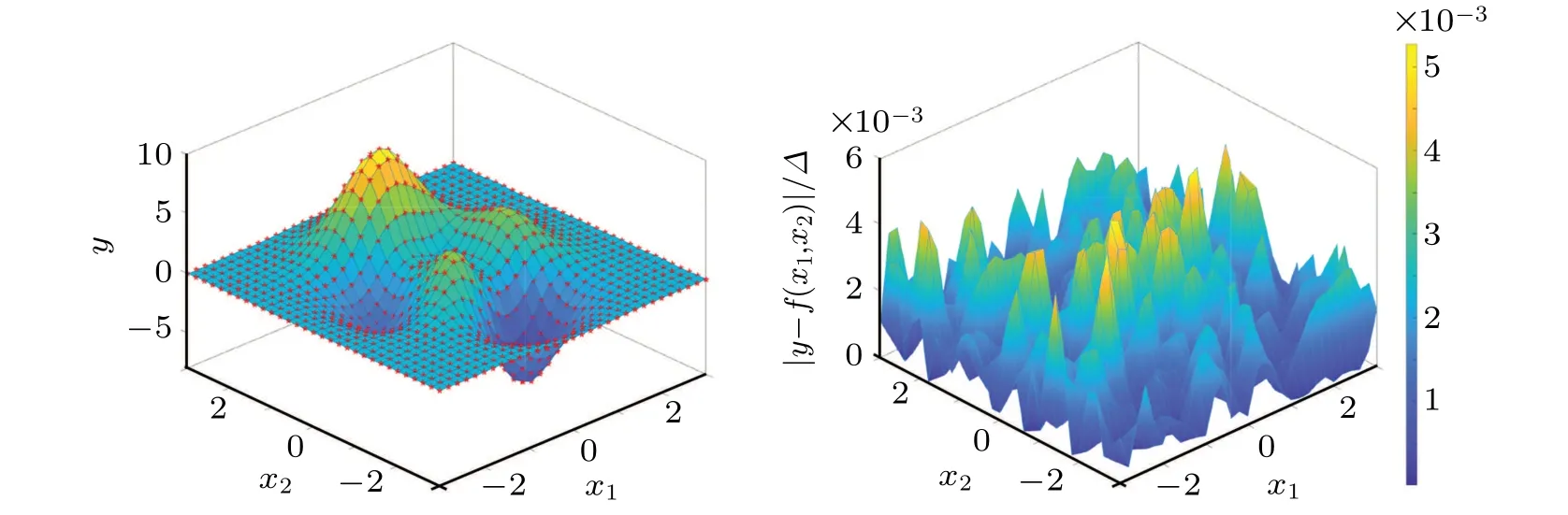
Fig. 6. (a) Network outputs y of the trained threshold neural network by the Adam optimizer as the approximation (patched surface) to the 32×32 testing data(⋆)of the two-dimensional function f(x1,x2)in Eq.(8). (b)The corresponding relative error|y−f(x1,x2)|/∆between the threshold network output and the testing data. For reference,the maximum difference ∆=max f(x1,x2)−min f(x1,x2)=13.4628 is taken for the target function in Eq.(8)in the range[−3,3]×[−3,3].

2.4. Real world data set of the function regression

We also validate the trainedN×20×1 threshold network on nine real-world data sets.[42–50]The dimensionNand the lengthLof data sets are listed in Table 1,and the computer is equipped with CPU of Intel Core i7-6700@3.40 GHz and 16G RAM DDR4@2133 MHz. Using the two-eight rule, 80% of data are used for training,while 20%of data are employed to test the trained threshold neural network. Table 2 reports the training and testing results of the MSEJmseof the stochastic resonance based threshold neural network for two considered optimizers. It is seen in Table 2 that the Adam optimizer can optimize the designed threshold network with a lower MSEJmsethan the SGD optimizer does in both training and testing data sets. The hyperparameter on-line learning of stochastic resonance based threshold networks via the Adam optimizer enables more precise control of injected noise levels in the hidden layer, leading to significantly improved performance of the designed threshold network.

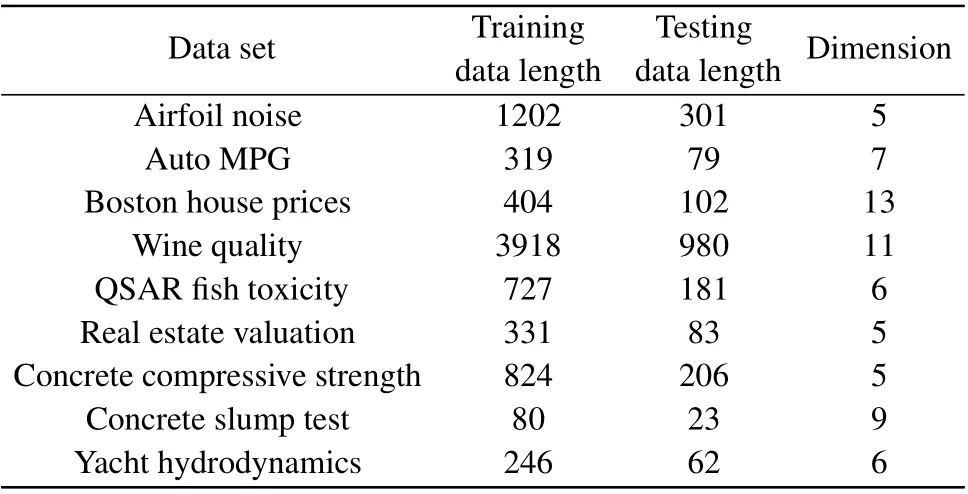
Table 1. Feature dimension and length of data sets.

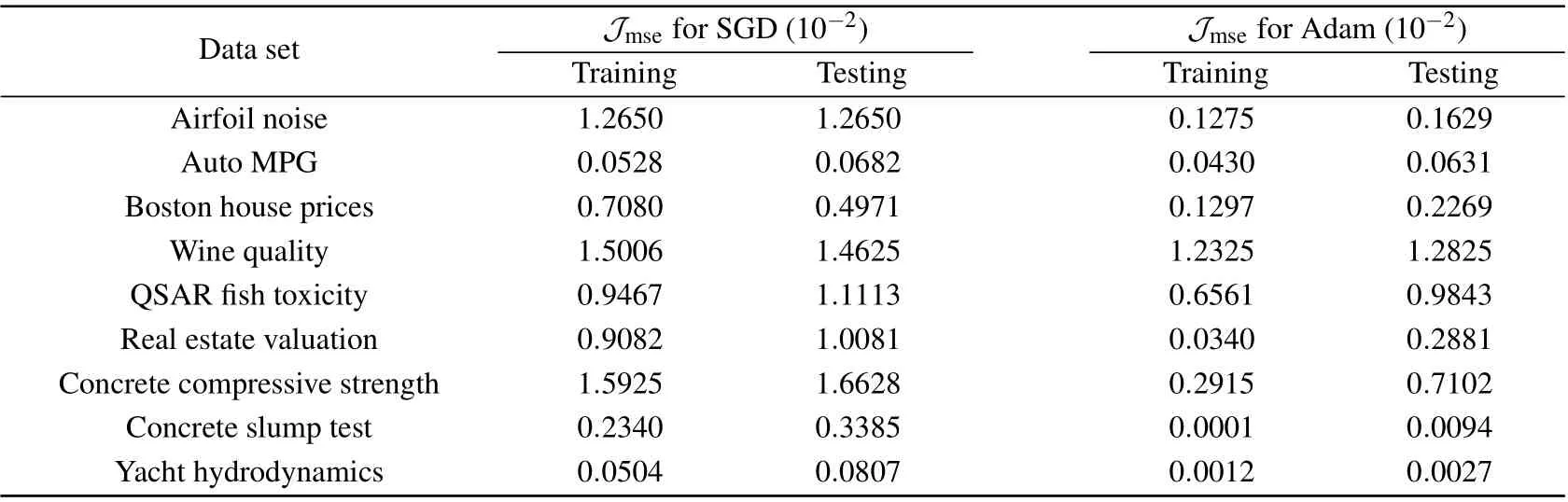
Table 2. Experimental results of the MSE Jmse of designed threshold threshold networks.

2.5. Recognition of handwritten digits

We further incorporate the expectation expression of Eq. (2) into the deep convolution neural network for image classification. The architecture of the deep convolution neural network contains 20 convolutional filters with the size 9×9 and the same padding, the hidden layer with 20 neurons indicated by Eq. (2), the factor-2 pooling layer, and the fully connected layers with 10 neurons. The benchmark data set of MNIST consists of a training set of 6×104and a testing set of 104gray-scale images(28×28)representing the handwritten digits from 0 to 9. Here, we employ 104images with the training set and the test set in a ratio 4:1. Using the SGD and Adam optimizers,the training accuracies of the designed convolution neural network versus the training epoch number are shown in Fig. 7. It is seen in Fig. 7 that the designed convolution neural network optimized by the Adam optimizer generally achieves a higher accuracy for recognizing handwritten digits. For the well trained convolution neural network after 50 training epochs,usingT=10 threshold functions assisted by the injected noise with the same size,the experimental accuracy rate in the test set is 98.41% for the Adam optimizer and 97.63% for the SGD optimizer, respectively. For comparison,it is noted that the full-connected backward propagation network[29]and the support vector machine[51]achieve the accuracy rates of 97%and 94.1%,respectively. The accuracy rate 98.41%obtained by the trained convolution threshold neural network by the Adam optimizer indicates a very satisfactory efficiency of the deep learning method. These results demonstrate that the injection of noise into threshold neurons facilitates the optimization of the designed deep convolution neural network, and the hyperparameter on-line learning of the Adam optimizer can also train the deeper stochastic resonance based threshold networks for image classification with a competitive performance.

Fig.7.Learning curves of accuracies of the designed convolution neural network on the MNIST data set.

3. Conclusion

In summary,in order to optimize the threshold neural network in the training phase, we replace the zero-gradient activation function with the continuously differentiable function that is based on the PDF of the injected noise. However, this substitution strategy introduces a group of noise parameters related to the noise PDF,and poses challenges for the training algorithm. For function approximation and image classification,it is shown that,due to the hyperparameter on-line learning capacity,the Adam optimizer can speed up the training of the designed threshold neural network and overcome the local convergence problem existing in the SGD optimizer. More interestingly, the injected noise not only extends the dimension of the parameter space wherein the designed threshold network is optimized,but also converges to a nonzero noise level in each hidden neuron. This distinguishing feature is closely related to the adaptive stochastic resonance effect,and also indicates a meaningful application of the stochastic resonance phenomenon in artificial neural networks.

However,it is noted that the Adam optimizer can train the artificial neural network to fit the target function well or recognize labels in classification more correctly. Then,for noisy observations of a target function or the uncorrected labels,the overfitting problem may occur for the training process of the designed threshold network by the Adam optimizer. Noting the the regularization in the loss function contributed by the injected noise,[16,17]it is much more meaningful to further investigate the generalization performance of the stochastic resonance based threshold neural network,especially for the low signal-to-noise ratio of the acquired signals by sensors. In Eq. (2), only the Gaussian noise injected into the designed feed-forward threshold neural network is considered. It will be interesting to find the optimal injected noise type to achieve the improved performance of the designed threshold network with respect to the noise PDF.In addition,we test the convolution threshold neural network with the injection of noise on image classification of the MNIST data set, and the potential applications of this kind of deep convolution threshold neural networks on more challenging data set, e.g., CIFAR-10 and ImageNet,also deserve to be explored.

Acknowledgement

Project supported by the Natural Science Foundation of Shandong Province,China(Grant No.ZR2021MF051).