Spatial correlation of irreversible displacement in oscillatory-sheared metallic glasses

Shiheng Cui(崔世恒), Huashan Liu(刘华山), and Hailong Peng(彭海龙)

School of Materials Science and Engineering,Central South University,Changsha 410083,China

Keywords: metallic glasses,mechanical property,molecular dynamics

1. Introduction

Metallic glasses are promising in engineering application due to their unique mechanical properties stemming from the disordered atomic-level structure.[1–3]Merits of the disordered structure,however,are limited by the brittle fracture of the materials. When a region of irreversible rearrangement starts at locals of weakly-bonded atoms in the deformed amorphous solids,[4–8]the local plastic zone can trigger the birth of a newly merged plastic zone nearby.[9,10]Cascades of the plastic zones organize in space within a band due to the strong spatial correlation, and the band may eventually percolate the whole system,viz. the phenomenon of shear banding,[11–14]eventually leading to the catastrophe failure of the materials. Thus,the ultimate fate of the materials is determined by the spatial correlation of the plastic events in the disordered structure.

Despite numerous investigations on the mechanical response of amorphous solids, the decay behavior of the plastic correlation is still controversial. A first and intuitive expectation is that the correlation should decay fast to zero with distance due to the shear localization phenomenon commonly observed.[2,3,8]The finite range of the correlation advocates a typical length scale for such localized rearrangement,e.g.,the so-called shear transformation zones(STZs).[15,16]An exponential decay of the non-affine displacement manifests this case as that reported in a variety of glassy materials, including metallic glasses, Lennard–Jones mixtures, granular materials, and colloidal systems.[6,15,16]However, a power-law decay that is long-range correlation has also been reported in colloidal glasses, which implies a non-vanishing length scale for the plastic events.[17,18]There is evidence that the exponential decay observed could be due to the finite size effect,which truncates the power-law decay in large systems into a spurious exponential decay in small systems.[19,20]

Besides the finite-size effect,correlation anisotropy is another important factor to affect the decay formula of the correlations. Any local irreversible rearrangement induced by non-affine displacements can be considered as an Eshelby inclusion that generates a quadrupole-like stress field in the surrounding matrix.[21]Interaction of different local plastic events, thus, is maximum in the quadrupolar directions. This certainly affects the correlation decay of non-affine displacement. In the short-time interval where the harmonic response approximates,i.e., in the zero-load limit, the four-fold angular symmetry has even been observed for the non-affine correlations in the sheared two-dimensional (2D) Lennard–Jones solids.[22,23]Since the macroscopic response of glasses is largely determined by the organization of plastic events in relatively large time scale, how the correlation will behavior like,especially by the effect of anisotropy,is important to understand the mechanical properties of glasses.

In this study,we performed classical molecular-dynamics(MD) simulations on CuZr metallic glasses (MGs) with an oscillatory shear at different amplitudes. Benefit of the oscillatory shear is that we can simply quantify the irreversible displacement of atoms by square displacement field at comparing two configurations of zero strains,i.e., one is before shear loading and the other one is after shear unloading.This quantification does not involve the process of subtracting affine component as that essentially needs in continuous shear.[4]Another advantage is that a sharp yielding transition can be clearly observed under oscillatory shear,e.g.,in terms of the bifurcation of potential energy hysteresis,[24]diffusive transition,[25]and irreversibility transition at yielding.[26]

2. Simulation details

We conducted MD simulations on Cu50Zr50alloys with the embedded atom method (EAM) potential, utilizing the force filed parameters that has been proved to be adequate to describe the amorphous state of Cu–Zr metallic glasses.[27]The alloys was first equilibrated at 2000 K,with the atoms are randomly placed in configuration space, then cooled down to zero temperature at a cooling rate of 2.0×1012K/s. During cooling the NPT ensemble(constant particle number,constant pressure,and linear-scaled temperature with simulation steps)was utilized to adjust the simulation box to give zero pressure in every dimension. The simulation time step is 1 fs at the cooling process,while is 2 fs at shear deformation. The oscillatory shear was performed using athermal quasistatic shear(AQS) protocol, which is the deformation under quasistatic conductions.[28]In this procedure, the system is always kept in local potential energy minimums while ignoring the effect of thermal activation. Specifically, the particle position was firstly deformed affinely according to:r′x=rx+dγry,withdγ= 4×10−3the elementary strain increment in every step. Then, the system is relaxed into the nearest local potential energy minimum via energy minimization using the conjugate gradient algorithm. This procedure is repeated until the strain reaches the amplitudeγmax. Then,shear direction is instantaneously reversed until−γmaxarrives. A full circle of the oscillatory shear includes the strain change:0→γmax→0→−γmax→0. All the simulations were performed via software package LAMMPS,[29]withN=5000 atoms included in the simulation box. A bigger system withN=4×104atoms is simulated to check the finite size effect.More simulation details can be also found in Ref.[30].

3. Results and discussion

Oscillatory shear was applied on the samples with a variety of shear amplitudes,i.e.,γmax=0.05, 0.06, 0.07, 0.08,0.09, 0.1, 0.11, 0.12, 0.13, for totally 200 cycle times. At small(γmax<0.08)and large(γmax>0.1)amplitudes,potential energy of the system reaches the steady state up to twenty cycling times, while up to forty cycling times in between.This is consistent with the critical behavior,i.e., a diverging critical cycling times,found at the yielding of Lennard–Jones systems.[31]We are interested in the steady state that the system reached after the critical shear times, and all the results shown in the following are obtained in this regime. Here the steady state is referred either to the limited configurations the system periodically visits at small strain amplitudes or to the plastic-flow regime at large strain amplitudes (typically relative to the yielding strain).[25,31]

An exemplary of the mechanical response for the MGs during 3-cycling times in the steady state was shown in Fig.1.Atγmax≤0.09, the shear stress shows a straight linear relationship with cycling time,which indicates an elastic response for the alloys. Atγmax>0.09, this linear response is clearly to be destroyed, with the maximum stress the system reaches dropping down comparing to the one atγmax=0.09. Interestingly, the stress is non-zero when the strain is zero (at the position when the cycle number is an integer) in this regime.This is clearly the clue that the alloys experiences viscoelastic response, as the phase lag between stress and strain emerges.By this,we conclude that the yielding point can be unambiguously determined atγ=0.09 in this metallic glass.

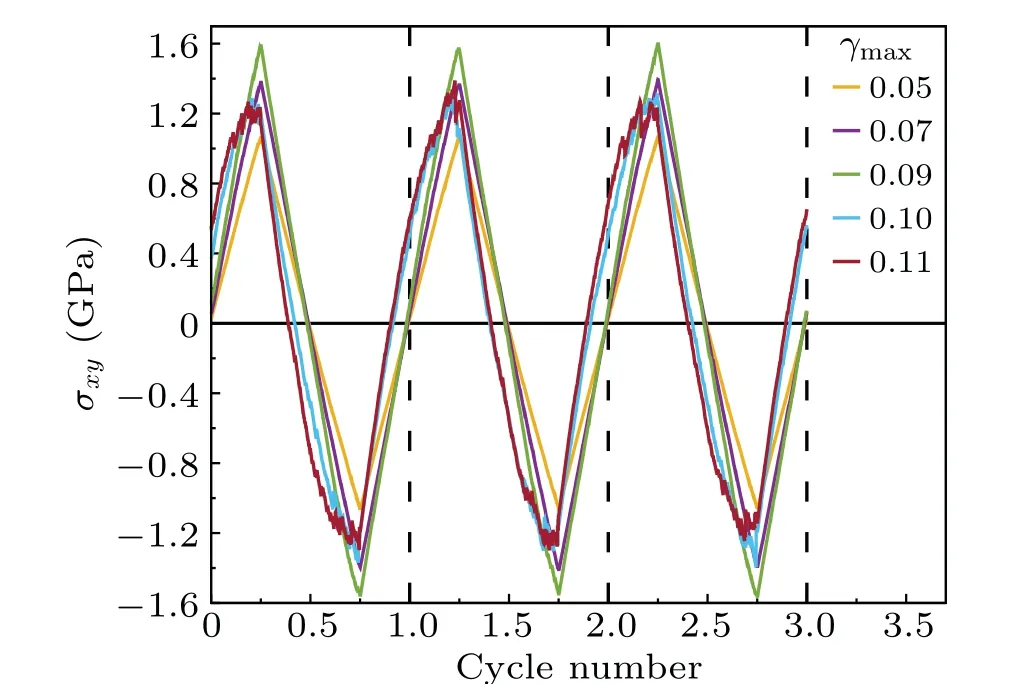
Fig.1. The stress evolution of CuZr metallic glasses under oscillatory shear for the selected 3-cycling time in the steady state. This picture has been updated.

A clear-cut definition of yielding point can also be seen from the maximum stress the system reached in the oscillatory shear,[24]which is in contrast to the difficulty of determining yield strain in continuous loading process. The maximum stress in steady regime is shown in Fig. 2(a). A clear transition happens at the yielding pointγY(=0.09)in the large system (N=4×104), while it is not so obvious in the small system(N=5×103). This yielding point can be validated in terms of the stress evolution during the loop, which is found to be small difference during the loading and unloading process atγmax≤0.09, while a significant hysteresis emerges atγmax> 0.09 (Fig. 2(b)). This is consistent with the results found in Fig.1.

Usually,the yielding transition is connected with the percolation of the localized plastic regions throughout the system,i.e., the shear banding phenomenon. We checked that the square displacement of atoms in the adjacent zero-strain configurations at different strain amplitudes(Figs.2(c)–2(f)),finding the plastic regions indeed concentrate in a narrow plane atγmax>γY,i.e., formation of a shear band (SB), inN=4×104system. However, we do not find a clear SB inN=5×103after yielding,which could be due to the fact that the box length is too small to let an SB nucleate. This would explain the absence of the sharp transition found in Fig. 1(a)for the small system size.

Fig.2.(a)Maximum shear stress obtained during the oscillatory shear in the steady state for N=5×103 and N=4×104 atoms system.(b)Stress versus strain in the steady state at different shear amplitudes. (c)–(f)Visualization of atomic displacement in the time interval of half oscillating periodicity at different strain amplitudes for N=4×104 system.

Correlation of the local plastic events is important to understand the macroscopic behavior of metallic glasses, as it gives the clue how the local events organize in space. To this end, we calculated the spatial correlation function of square displacement, ∆r2, in the adjacent of two zero-strain configurations. As the system is athermal, ∆r2represents the nonaffine response of atoms as that in continuous shear deformation. The correlation functionC(r)is defined as

We constrain the analysis in the shear plane (θ=π/2), and typically choose four different directions (φ=0.5π,1.0π,1.5π, and 2.0π). In small system correlations of different directions collapse together both in elastic and plastic regime (see Figs. 3(a)–3(c)), indicating an isotropic behavior of the irreversible correlation. This is in the scenario of homogeneous deformation even beyond the yielding point

where no SB is observed. Decay of the correlator exhibits an exponential formula(see the straight dashed lines in top panels of Fig. 3),C(r)∼e−r/ξ, withξthe characteristic length for the ensemble of plastic events.ξis found to be around one atomic diameter(which is about 2.7 ˚A defined as the first maximum position in pair distribution function) in the elastic regime, and increases beyond one diameter in the plastic regime. The exponential decay of the correlator and the value of the characteristic length is consistent with results reported elsewhere.[6,15,16]

Situation changes in large system. Although the correlator is isotropic and in the exponential decay in elastic regime similar to that in small system, the decay clearly deviates in different directions atγmax≥0.09 (bottom panels in Fig. 3).Specifically,correlation of irreversible displacement is still under exponential decay in the normal direction of the SB plane,with the characteristic length increasing with strain amplitude.In contrast, it decays quite slowly in the direction parallel to the SB plane in an algebraic formula,C(r)∼r−β, with the value ofβstrongly fluctuating with strain amplitude.

The discrepant decaying behavior is ascribed to the homogeneous or inhomogeneous yielding transition. In small system the deformation is homogenous even atγmax>γY,

where no SB can be observed. The correlation of irreversible displacement, then, displays as an isotropic and exponential decay. It is similar for large system in elastic regime as the deformation is still homogenous. BeyondγYstrong anisotropy emerges due to the generation of SB. An exponential decay in the normal direction of SB may imply the finite width of the SB,while the algebraic decay in the parallel direction indicates the strong interaction between plastic events that organizes inside this plane. It should be noted that amorphous solids are not necessarily to be deformed or ruptured in an inhomogeneous matter, as temperature levitation can induce a homogenous-to-inhomogeneous transition or brittle-to-ductile transition.[32]This would rationalize the discrepant decaying formula of the plastic correlations reported before.[6,15–18]

Fig.3. Correlation of square displacement in small system(top panels)and in large system(bottom panels)under oscillatory shear. Note that panels(a)–(d)show the correlation function in semilog plot,while panels(e)–(f)in double log plot.

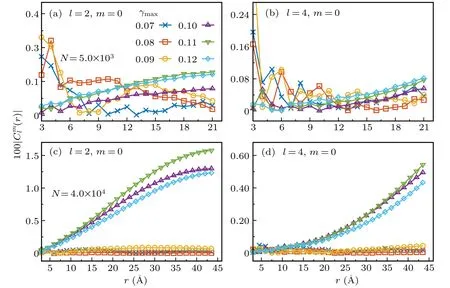
Fig. 4. Correlation anisotropy of the square displacement for polar (a) and quadrupolar (b) symmetries in a small system, and for the same symmetries[(c)–(d)]in a large system under oscillatory shear. Only the order m of the strongest signal is shown here.

Different decaying formula at different directions is due to the nature of anisotropy. To quantify the anisotropic behavior,we project the azimuthal-dependent correlator onto spherical harmonics,Yml,similar to the anisotropic characterization of pair distribution functions:[33]

The obtained anisotropic signal is finite,but much weaker in the small system than that in the large system(see Fig.4).This is expected as the deformation is almost homogeneous in small system as alluded above. In large system a clear increment of the signal with distance can be found atγ>γY,consistent with the deviated correlation functions in different directions (see Fig. 3). The emerged polar symmetry could be due to the emergency of shear band, while the quadrupolar symmetry could be due to the quadrupolar filed generated by Eshelby inclusion as that reported in 2D Lennard–Jones solids.[22,23]But it should be noted that the intensity of polar is much stronger than the one of quadrupolar. Thus,the polar symmetry is the dominant anisotropy in this case. The spectrum saturates at large distance for polar symmetry, whereas it still shows an increasing tendency at the maximum distance that can be achieved in the large system investigated. This may indicate that the typical length scale for the quadrupolar symmetry is larger than the one of the polar symmetry.

4. Conclusions

Classic molecular-dynamics simulations were performed on the oscillatory shear of CuZr metallic glasses to investigate the spatial correlation of irreversible displacement. We find the decay of the correlation is isotropic and exponential-like in the small system, where the deformation is homogeneous;the correlator is anisotropic in the large system,where the deformation is inhomogeneous as evidenced by the formation of shear band. It shows the exponential decay in the normal direction,while the power-law decay in the parallel direction to the shear band plane. By projecting the azimuthal-dependent correlation function,we found a strong polar symmetry,and a weaker quadrupolar symmetry after yielding in the large system. Thus,we conclude that the anisotropic correlation of irreversible displacement is dominated by the inhomogeneity of the plastic deformation in the metallic glasses.

Acknowledgements

The authors acknowledge the computer resources provided by High Performance Computing Cluster(HPC)of Central South University.

Project supported by the Natural Science Foundation of Hunan Province,China(Grant No.2021JJ30833).