Low-temperature heat transport of the zigzag spin-chain compound SrEr2O4
Liguo Chu(褚利国) Shuangkui Guang(光双魁) Haidong Zhou(周海东)Hong Zhu(朱弘) and Xuefeng Sun(孙学峰)
1Department of Physics,Key Laboratory of Strongly-Coupled Quantum Matter Physics(CAS),University of Science and Technology of China,Hefei 230026,China
2Department of Physics and Astronomy,University of Tennessee,Knoxville,Tennessee 37996-1200,USA
3Institute of Physical Science and Information Technology,Anhui University,Hefei 230601,China
Keywords: spin chain,quantum spin system,thermal conductivity
1. Introduction
Quantum effects are enhanced in those antiferromagnetic (AF) systems with small spins, low dimensionality or spin frustration. The famous quantum spin systems in lowdimensional cases are theS=1/2 Heisenberg chain and theS=1 Haldane chain,which can exhibit gapless spin liquid or spin gapped ground state.[1–4]Geometrically frustrated magnets,in which the magnetic interactions are incompatible with the underlying lattice symmetry, have attracted much attention. In such systems, the competitive interactions prohibit the energy-minimized local spin configuration from extending globally, and result in a macroscopically degenerate ground state in which many novel magnetic behaviors can emerge.Even in rare-earth compounds where the anisotropic moments induced by spin–orbit coupling are commonly regarded as the classical ones in the low temperature limit, with the help of magnetic frustration,some novel magnetic properties have been discovered experimentally.[5–7]
SrEr2O4belongs to the family of isostructural magnetically frustrated compoundsAB2O4(A= Sr, Ba andB=lanthanide).[8]In these materials,theBions are located inside two kinds of differently distorted oxygen octahedrons,resulting in two magnetically inequivalentBsites. In SrEr2O4, the two sets of Er magnetic moments form two different zigzag Ising spin chains along thecaxis, which connect with each other to form a distorted honeycomb sublattice with the honeycomb layer perpendicular to the chain direction, as shown in Fig.1. Thus,this material is a special one-dimensional and frustrated spin system.The intra-chain and inter-chain spin exchanges have not been determined experimentally. However,the magnetic susceptibility data demonstrated a rather large Curie–Weiss temperatureθCWof−13.5 K, compared to the N´eel temperatureTNof 0.75 K.[9]Actually,the previous studies revealed some unusual magnetic properties in SrEr2O4. At low temperatures there is the coexistence of AF long-range order(LRO)and incommensurate short-range order(SRO)involving Er1 sites and Er2 sites, respectively.[9,10]It was also determined that the magnetic moments on Er1 sites and Er2 sites point toward thec-axis anda-axis directions, respectively. ForB||a,a 1/3 magnetization plateau was observed and indicated a field-induced two-spin-up one-spin-down (UUD)phase.[11]
It has been known that the heat transport of lowdimensional spin systems exhibit many interesting properties due to the possible transport of magnetic excitations and the spin–phonon scattering. In particular, large magnetic heat transport has been found in some one-dimensional and two-dimensional spin systems.[12–14]In some frustrated spin systems, the peculiar spinon excitations associated with the quantum spin liquid state have also been found to transport heat.[15–17]However, in more spin frustrated materials the magnetic excitation seems to scatter phonons rather than to carry heat.[18,19]In this work, we study the magnetic and heat-transport properties of SrEr2O4single crystals by using magnetic susceptibility, specific heat and thermal conductivity measurements at very low temperatures down to 0.3 K and in high magnetic fields up to 14 T. Thermal conductivity results indicate that phonons are the main heat carriers in this material, while magnetic excitations play a role of scattering phonons.
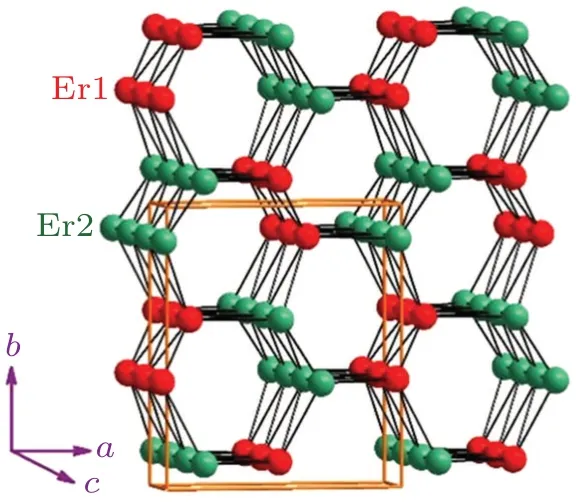
Fig.1. Schematic plot of the crystal structure of SrEr2O4,in which Er ions on two inequivalent sites form two zigzag chains. The other atoms are omitted for clarity.
2. Experiment
High-quality SrEr2O4single crystals were grown by using the floating-zone technique. The x-ray backscattering Laue photographs as well as x-ray diffraction were used for identifying the crystal quality and crystallographic directions.Large pieces of crystals were cut into long bar-shaped samples along the crystallographic axes for the thermal conductivity measurements, which were carried out in a3He refrigerator equipped with a 14-T magnet.[18,19]The specific heat was measured by the relaxation method in the temperature range from 0.4 K to 30 K on a physical property measurement system (PPMS, Quantum Design). Magnetization and magnetic susceptibility were measured using a Quantum Design superconducting quantum interference device with a vibrating sample magnetometer (SQUID-VSM), equipped with a3He refrigerator insert. For all measurements above, the magnetic field were applied along theaaxis orcaxis.
3. Results and discussion
3.1. Magnetic susceptibility and magnetization
Figure 2(a)shows the temperature dependence of magnetizationM(T)at 1.7 K to 0.45 K and in various magnetic fields along thecaxis. In 0.01-T field,a clear drop of magnetization occurs at 0.75 K, which indicates an AF phase transition according to the previous works.[9,11]BelowTN=0.75 K, theM(T)curves tend to approach finite values as temperature decreases. The transition temperature decreases with increasing field to 0.1 T and meanwhile the drop becomes weaker. AtB=0.4 T the drop is replaced by a slope change ofM(T)at∼0.7 K. With further increasing field, theM(T) curves display a monotonic increase with decreasing temperature, indicating that the Er1 sublattice enters a high-field polarized state.Figure 2(b) shows the results of the zero-field cooling (ZFC)and field cooling(FC)data ofM(T)forB||aat 0.45 K and 1 K.Spin freezing behavior in this material can be excluded since there is no significant difference between the FC and ZFC data.ForB=0.1 T,theM(T)has a broad peak at 0.75 K,which is also due to the AF transition.

Fig.2. (a)Magnetization measured at the temperature from 0.45 K to 1.7 K with various magnetic fields along the c axis. (b)Magnetization with fields along the a axis obtained both after ZFC and FC procedures. (c) and (e)Magnetization curves of SrEr2O4 single crystals at 0.45 K and 1 K with magnetic field along the c axis and a axis,respectively. (d)and(f)The differential curves of the magnetization dM/dB corresponding to panels (c)and(e).


3.2. Specific heat
Figure 3 shows the temperature dependence of specific heat of SrEr2O4single crystal in various magnetic fields along two different crystallographic axes. The zero-field data shows a sharpλ-type peak atTN∼0.73 K, which is attributed to the long-range AF transition.[9]Besides,there is a large broad peak at low temperatures,indicating significant magnetic contributions from the short-range spin correlation or crystal field effect(CEF)of Er3+ions.
In order to extract the magnetic contribution to the lowtemperature specific heat, other terms such as phonon specific heat(Cph),nuclear Schottky specific heat(Cn),and crystal field Schottky specific heat (CCEF) should be determined and subtracted from the measured data. The nuclear Schottky specific heat from Er3+nuclear moment is negligibly small in the present temperature range,[20,21]hence it could be ignored without causing considerable errors. It is known that the Er3+multiplet4I15/2splits into eight Kramers doublets in the distorted octahedral crystal field.[22]Therefore, we take these low-lying CEF energy levels to calculateCCEFby using a multi-level Schottky specific heat expression:[23]

whereεiorεj(i,j=0,1,2,3,4)is one of the five lower sublevels of the splitting4I15/2multiplet of which the magnitudes were determined in Ref.[14],giorgjis the degeneracy of each energy level,andRis the universal gas constant. Two sets of the crystal field energy levels for the two crystallographically inequivalent Er3+ions were substituted into Eq.(1)to calculate theirCCEF,as shown in Figs.3(a)and 3(c). After subtracting the CEF contribution,the remaining terms of specific heat are plotted in Figs.3(b)and 3(d).
To further subtract the contribution of phononsCph, a truncated odd-order Taylor series expansionCph(T)=β3T3+β5T5+β7T7was used to fit the zero-field data at high temperatures.[24]The results of fitting are shown by the black dashed lines in Figs. 3(b) and 3(d). Based on the approximation formulaβ3=(12/5)π4nAR/(θD),the obtained fitting parameterβ3=1.52×10−4J/K4·mol gives a Debye temperatureΘD=447 K, which is comparable to that (460 K) obtained from the thermal expansion experiment.[25]Here,nAis the number of atoms in each molecule.

Fig.3. Low temperature specific heat of SrEr2O4 single crystals measured with magnetic field B c (a) and Ba (c). CCEF is the calculated CEF specific heat which is described in details in the main text. (b)and(d)Remaining specific heat after subtracting the CEF contribution for Bc and Ba,respectively. The black dashed lines show the fitted results of phonon specific heat by using a Taylor series expansion. Inset: the zoom-in of the low-temperature data at zero field.
The magnetic contribution to specific heatCmis obtained usingCm=C −CCEF−Cphand is plotted in Fig. 4. At zero field,besides the small and sharpλ-type peak atTN∼0.73 K,there is a broad peak at∼1.3 K, which should be related to the development of the incommensurate short-range magnetic order.[9]For, theλ-type peak is completely smeared out by a magnetic field as low as 0.2 T. The broad peak shifts slightly to lower temperature with applying weak fields(≤1 T), which rules out the possibility of the Schottky origin. For, as the magnetic field increases theλpeak shifts to lower temperatures, which is a typical result for an AF system. At the same time, the peak becomes lower and broader but is still discernible with increasing field up to 1 T.It is worth noting that the broad peak does not change with applying weak magnetic fields(≤1 T)but is strongly affected by higher fields. Nevertheless,the magnetic specific heat data indicate strong magnetic fluctuations in this low-dimensional spin system.
SrEr2O4belongs to a family of geometrically frustrated magnets with the chemical formulaAB2O4,most of which can be described by the one-dimensional (1D) axial next-nearest neighbor Ising(ANNNI)model.[26,27]Indeed,SrEr2O4shows some characteristics of 1D ANNNI model, such as a double N´eel ground state and a 1/3 magnetization plateau in the intermediate field.[28–30]However, the rigorous ANNNI model may not be fully applicable to SrEr2O4. Theoretical calculation and experimental results verified the existence of a specific heat peak whose position changes with magnetic field.[31–33]This is a bit different from what we observed in SrEr2O4.
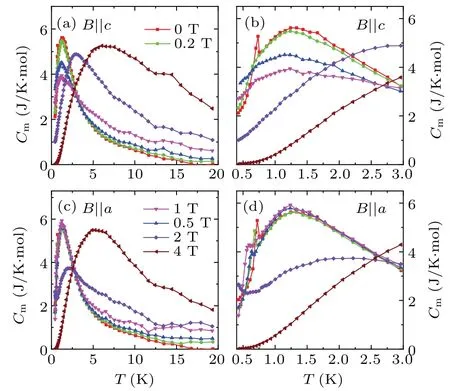
Fig. 4. Magnetic specifci heat of SrEr2O4 in various magnetic feilds forc(a)and Ba(c). (b)and(d)Zoom in of data for T <3 K.
3.3. Thermal conductivity
Figure 5 shows the temperature dependence of thermal conductivityκof SrEr2O4single crystals in various magnetic fields with heat current along theaaxis orcaxis and at temperatures from 0.3 K to 30 K.The inset shows the comparison ofκaandκcin zero field. They show a nearly isotropic behavior except for slight difference at low temperatures. Since SrEr2O4has a low-dimensional spin system,in which the exchange coupling along thecaxis is much stronger than that along theaaxis,the isotropic heat transport indicates that the spin excitations mainly play a role of scattering phonons rather than carrying heat. This is further confirmed by the strong increase ofκin high magnetic fields, which can be attributed to the suppression of magnetic excitations by high fields. At very low temperatures,the phonon thermal conductivity tends to follow aT3temperature dependence known as the boundary scattering limit.[34]Hence, the change of the zero-fieldT1.5power law dependence ofκctoT2.5in 14-T field, as shown in Fig. 5(c), demonstrates that the magnetic excitations scattering of phonon is significantly suppressed by such a large magnetic field, and theT3behavior tends to be established.Another feature of the zero-fieldκ(T)data is the kink around 1.2 K, which has some correspondence to the broad peak of magnetic specific heat. Apparently,the magnetic fluctuations evidenced by the specific heat can induce strong scattering of phonons.[35–38]
Figures 6 and 7 show the low-temperature magnetic field dependences ofκaandκc,respectively,for fields up to 14 T.A notable result is that the field dependence ofκis mainly determined by the field direction rather than heat current direction,which can be attributed to the anisotropic magnetic properties. This also indicates that there is no sizeable magnetic heat transport in this low-dimensional spin system.

Fig. 5. Temperature dependences of thermal conductivity along the a axis(κa) and that along the c axis (κc) of SrEr2O4 single crystals for magnetic field applied along either the a axis or the c axis. The inset shows the zerofield κa and κc for comparison.

Fig. 6. Magnetic field dependences of κa at low temperatures with field applied along either the a axis or c axis.
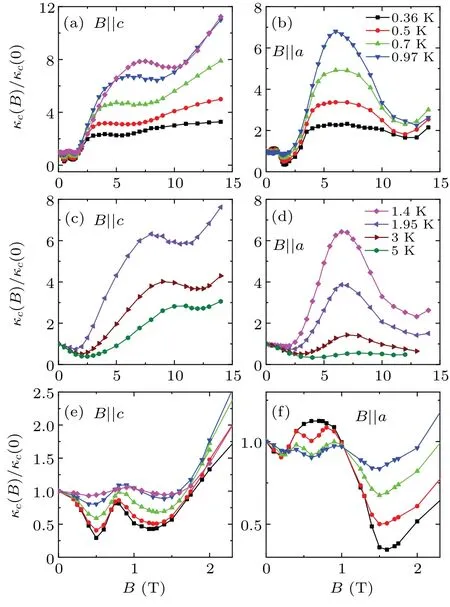
Fig. 7. Magnetic field dependences of κc at low temperatures with field applied along either the a axis or c axis.


4. Summary
In summary, the thermal conductivity, magnetic susceptibility, and specific heat at very low temperatures are studied for SrEr2O4single crystals, which is known as a frustrated zigzag spin chain system. The magnetic field induced magnetic transitions for eitherB||corB||aare characterized by magnetization results, while the specific heat data indicates strong spin fluctuations at low temperature. The thermal conductivity shows strong magnetic field dependence,indicating the strong coupling between phonons and magnetic excitations. At very low temperatures, the magnetic transitions induce minima at theκ(B)isotherms and high magnetic field induces a strong increase ofκ. These results indicate that the low-temperature thermal conductivity of this material are mainly contributed by phonons,while magnetic excitations play a role of scattering phonons.
Acknowledgements
We thank Jichuan Wu for helps on experiments. Project supported by the National Natural Science Foundation of China (Grant Nos. U1832209 and 11874336). The work at the University of Tennessee(H D Zhao)was supported by the NSF with Grant No.NSF-DMR-2003117.
- Chinese Physics B的其它文章
- Magnetic properties of oxides and silicon single crystals
- Non-universal Fermi polaron in quasi two-dimensional quantum gases
- Purification in entanglement distribution with deep quantum neural network
- New insight into the mechanism of DNA polymerase I revealed by single-molecule FRET studies of Klenow fragment
- A 4×4 metal-semiconductor-metal rectangular deep-ultraviolet detector array of Ga2O3 photoconductor with high photo response
- Wake-up effect in Hf0.4Zr0.6O2 ferroelectric thin-film capacitors under a cycling electric field

