基于投影寻踪—灰色理论的多地区电网投资决策方法
殷旭锋
(广东电网有限责任公司江门供电局,广东 江门 529000)
0 引言
电力发展规划中明确提出,电网效益评价准确度对于实现电网精细化管理有着重要作用。传统依赖于专家打分和指标体系的评价方法,指标权重易受不确定性因素影响,难以实现精确量化。针对复杂电网脆弱节点辨识困难问题,现有文献提出了以下解决方法:一是层次分析法—灰色关联度的综合评估模型,实现了专家经验主观性和节点数据客观性的良好结合[1];二是一种基于电网安全运营视角的综合评价方法,但是对于如何降低主观因素的干扰并未说明[2];三是对主客观权重进行了融合,但其在主客观权重融合时未阐述方法的合理性[3]。而模糊综合评估和区间数评估理论,则利用线性方法求解权重,结果易受单一因素影响导致评估信息不够全面[4]。
在电网企业投资分配决策方面,目前已有部分学者展开研究。这些研究从宏观上对电网投资效益进行总体评价,微观上对电网投资效益进行单体评价,根据效益评估结果进行等比例经费分配,但忽略了投资效益最大化的提升要求[5]。根据电网项目投资的经济性、可靠性以及发展性建立投资组合模型的多目标函数,通过变权理论投资决策量化模型的优化求解,突出了不同企业的投资重点,但考虑的因素有限,无法基于各地区电网发展状况进行预算分配[6-8]。
综上所述,现有文献针对指标权重的研究具有一定的主观性,且缺乏对各地区电网经费合理分配等方面的研究。本文引入投影寻踪—灰色理论来评价各地区电网效益,可实现预算资金的合理分配,提升电网精细化管理水平。
1 地区电网投资能力评估指标体系
对于电网而言,投资能力的评估研究对于电网实现合理投资规模的确定具有较强的战略意义。根据地区电网发展状况与运行特点,构建的指标体系要考虑经济、规模、运营、社会4个方面。地区电网综合投资能力评价指标体系如表1所示。

表1 地区电网投资能力综合评价指标体系
2 投影寻踪—灰色理论模型
2.1 投影寻踪模型
投影寻踪模型能够降低数据复杂性,保证数据处理的准确性。通过将高维数据投影转化为一维数组,进而分析数据样本特征。
2.1.1 数据标准化处理
电网企业综合效益评估的问题可以描述为:由m个待评估对象构成的集合为Q={Q1,Q2,…,Qm},n个指标构成的指标集为S={S1,S2,…,Sn},各指标具有不同的物理意义,评估矩阵为X=(Xij)m×n。采用极值法进行数据处理,公式如下
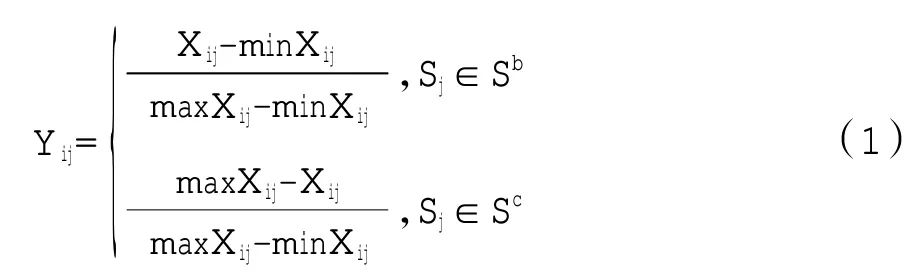
其中,max Xij和min Xij分别为第j个指标的最大值和最小值;Xij为指标的评价值;Sb和Sc分别为S中效益型和成本型指标的下标集。
2.1.2 构造投影指标函数
本质上,投影的主要目的是将高维数据映射到低维子空间,以寻找反映原高维数据结构的特征投影向量。对标准化评估矩阵Y进行投影,则Y在单位投影方向向量a上的投影值Pi为

其中,a=[a1,a2,…,an]为单位投影向量。
投影值的局部投影点需尽量凝聚成若干个点团,且点团之间应尽可能地散开。因此,投影指标函数可表示为
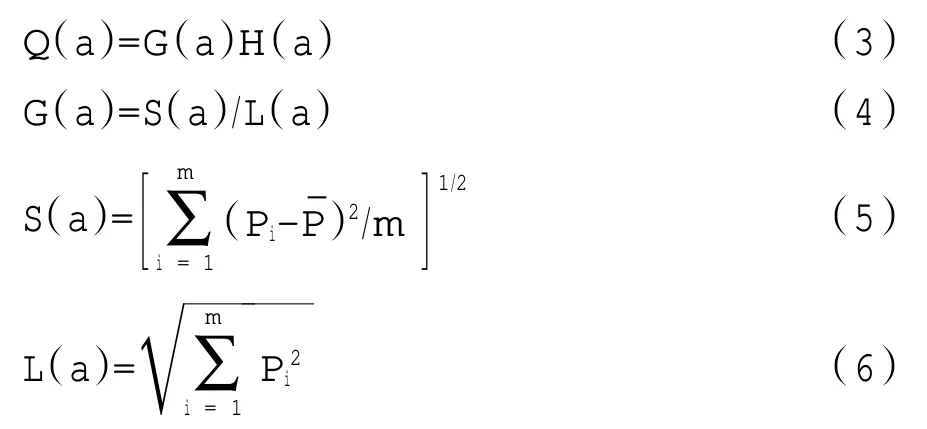
G(a)由Pi的标准差S(a)以及模长L(a)构成,为Pi的均值。
H(a)描述了投影后的局部密度点。H(a)可定义为
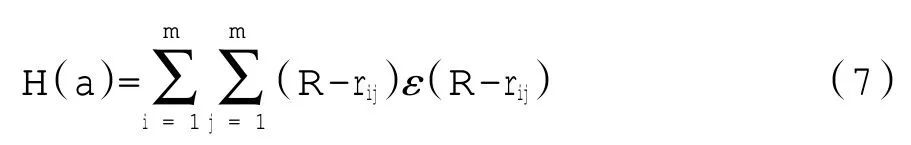
R表示局部密度的窗口半径,这里的R取值为0.1L(a);rij=|Pi-Pj|/L(a)表示样本之间的距离;ε(k)表示阶跃函数,k=R-rij,当k≥0时,ε(k)=1,当k<0时,ε(k)=0。
2.1.3 投影指标函数优化模型
在样本中指标评价值确定的情况下,Q(a)的大小与方向向量a有关。通过构造出最大化优化模型,就可以计算出最优投影向量。由于a为单位投影方向向量,满足,所以可将ω=(a12,a22,…,an2)作为指标权重向量。该模型能够体现不同指标对总体效益的影响程度,解决了权重确定中存在的主观因素影响问题。投影指标函数优化模型如下

2.2 灰色关联投影理论
灰色关联投影法将投影理论与灰色理论进行融合,对决策方案进行量化评价。灰色关联投影理论考虑不同方案之间的信息,避免单方向偏差[9]。
2.2.1 加权灰色关联矩阵
设Y0=(Y01,Y02,…,Y0j,…,Y0n)为理想样本参考序列,Y0j为第j个指标值的最大值。将Y0作为母因素,Yij作为子因素,可得二者之间的关联度eij为
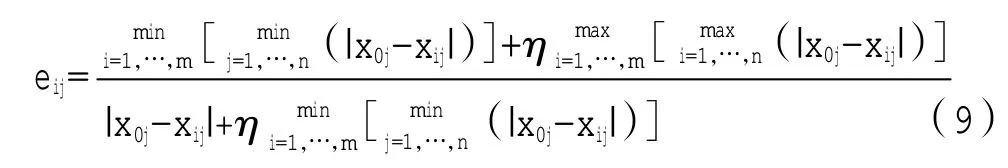
其中,η(0≤η≤1)为分辨系数,在实际应用中,通常人为规定η=0.5。由(m+1)×n个eij组成判断矩阵E=(eij)(m+1)×n,(i=0,1,2…,m;j=1,2…,n)。
2.2.2 灰色关联投影值
将每个待评方案作为一个行向量(矢量),θi为灰色关联投影角,ωj为指标权重列向量。待评方案Qi与理想方案Q0的夹角余弦为
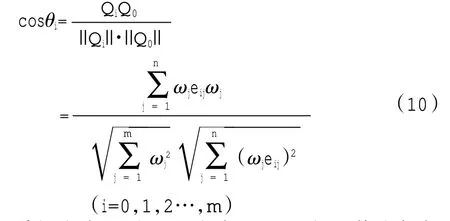
待评方案Qi在理想方案Q0上的投影值为灰色关联投影值Ti

以各被评估对象的Ti值作为效益度量标准,Ti值愈大,对应的评估对象效益值就越高。
3 基于效益的投资分配决策方案
依据灰色理论得到的电网效益评估值,实现电网投资决策的经费分配,使得电网综合效益最大化,同时使不同分配经费的分配结果与分配计划最小化,提高经营绩效,优化企业资源配置。本文建立多目标投资经费分配优化模型如下。

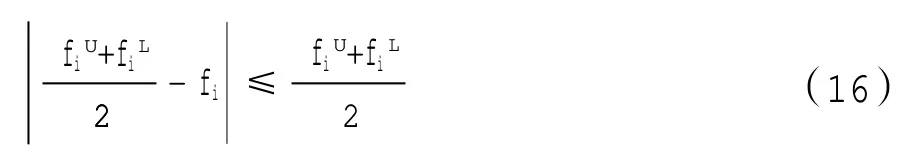
根据往年电网公司预算分配经费和实际分配经费情况,可以得到投资经费的申请准确度,记si为第i个地区电网公司申请的投资经费对应的申请准确度,则

记fi0(i=1,2,…,m)为第i个地区电网预测的投资经费,ti为第i个地区电网申请的投资额,则

其中,Ti为第i个地区电网投资能力综合效益值;各地区电网公司总投资经费为F;fiL,fiU为第i个地区电网对应规定投资下限和对应规定投资上限。
4 算例分析
本文选取隶属于某省下辖的Q1、Q2、Q3、Q44个地区电网作为研究对象。
4.1 投影寻踪模型确定指标权重
利用线性递减权重粒子群算法对投影指标函数优化模型进行求解。设置初始条件为:粒子群数目N=50个,学习因子U1=2,U2=2,最大迭代次数M=1 000次,umax=0.9,umin=0.4,计算出的各评估指标最佳投影方向及权重如表2所示。
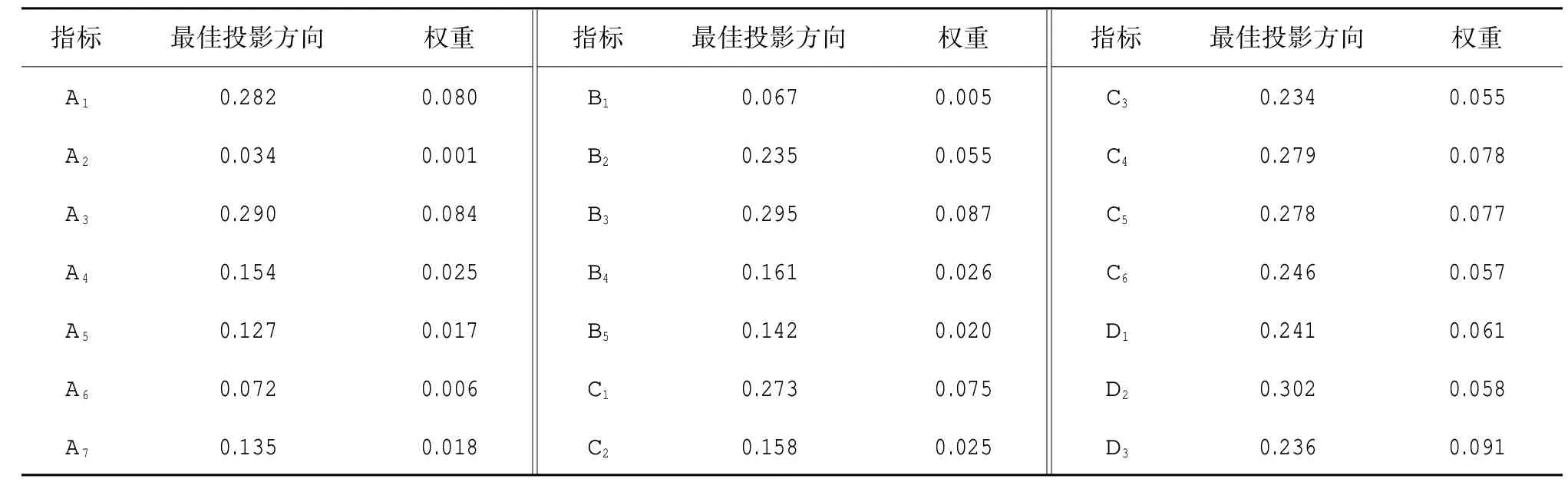
表2 指标最佳投影方向及权重
4.2 计算灰色关联投影值
由标准化后的判断矩阵可知,各待评指标的正理想解均为1。依据式(9)计算各指标下的灰色关联系数。依据式(11),结合各指标权重,可以计算出各地区电网企业的综合效益评估值。
4.3 投资经费决策分配
在满足各地区电网发展的同时,需要降低对低效或无效资产的投入,提高电网企业整体投资效益,进一步优化企业的资源配置。某省电网企业总投资经费预算为10.52亿元,各地区电网企业综合效益、投资能力、申请经费、申请准确度如表3所示。
采用上文中的投资分配模型进行求解。求解时先代入表3的数据,再利用gamultiobj函数求解,可得Q1=2.16亿元,Q2=2.80亿元,Q3=2.64亿元,Q4=2.92亿元。由此可见,本文所提出的投资经费决策模型为提高电网企业整体效益、优化资源配置提供了科学的决策方式。
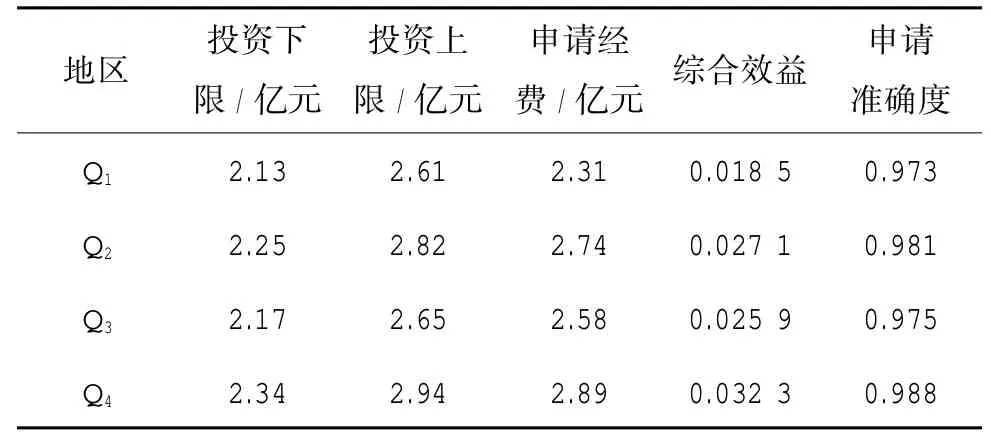
表3 各电网企业效益及投资经费情况
5 结束语
本文运用投影寻踪理论有效地解决了地区电网效益评估过程中指标权重的确定易受主观因素干扰的问题。结合灰色理论,通过求解灰色投影值来确定各地区电网的综合效益。实例案例表明,所提方法能够与实际结合,针对性地为电网企业效益评估以及投资决策提供一种新的方法。

