机场水泥道面日周期温度效应

凌建明，刘海伦，石 蓉，杨 帆，唐 龙

（1.同济大学道路与交通工程教育部重点实验室，上海 201804；2.同济大学民航飞行区设施耐久与运行安全重点实验室，上海 201804；3.四川省机场集团有限公司，四川成都 610000；4.民航机场规划设计研究总院有限公司，北京 110041）

温度变化对水泥道面性能影响显著。板内温度变化一方面影响板间接缝传荷能力［1］，另一方面也会导致道面板产生温度翘曲脱空，改变道面板受力模式［2］。此外，板内温度应力的存在，还会影响道面结构长期服役性能［3-4］。因此，深入研究水泥道面的温度影响对水泥道面的设计与评价具有重要意义。

水泥道面温度影响的研究方法包括理论解析法和试验研究法。1927年，Westergaard［5］基于Winkler地基推导了温度翘曲板的变形和应力解析解，奠定了理论解析法的基础；随后有限元数值求解的引入为理论解析提供了更为便捷的途径［6］。理论解析法虽然实施方便，但理想化的假定条件使其具有一定局限性。而试验研究法基于实测数据分析，是对理论解析法的验证和校正。国外相关试验研究以美国为代表：公路领域方面，美国于20世纪30年代在Arlington建立试验场［7］，之后又建立了Minnesota等多条试验路［8］，基于大量现场数据完善了其公路路面结构设计理论；机场领域方面，美国联邦航空局（FAA）于20世纪90年代在其国家机场道面设施实验室（NAPTF）进行了水泥道面的温度翘曲试验研究［9］，之后，又在Denver等多个国际机场道面中埋设大量传感器，分析环境-荷载耦合作用下机场道面的长期性能状况，以完善其机场道面设计与评价理论［10］。国内相关试验研究以同济大学为代表：公路领域，景天然等［11］、姚祖康等［12］基于现场数据分析了水泥路面板内温度应力，田波等［13］、李思李等［14］则着重研究了温度与层间结合的关系，相关研究完善了我国公路路面设计理论；机场领域，实测分析研究始于2014年［15］，仅在浦东国际机场［2，16］、松原查干湖机场［17］等少数机场具有实测数据。

综上可知，国内外研究主要服务于道面设计。近年来，随着研究逐步深入，温度对道面性能评价的影响逐渐引起重视［18］。其中，兼具平均温度变化和温度梯度变化的日周期温度，对道面性能评价的影响更为显著。然而，受限于机场飞行区封闭性的特殊要求，国内目前缺乏系统的实测数据，亟需补充完善。

为此，本文利用我国西南某国际机场跑道道面的温度、应变及弯沉实测数据，分析日周期内机场水泥道面的温度效应，揭示机场水泥道面日周期内的温度效应规律，为完善我国机场水泥道面性能评价理论提供参考。

1 试验方案

1.1 道面信息

本试验依托西南某国际机场工程，试验地属亚热带季风性湿润气候，气候温和。试验板位于机场某跑道中线东侧第二列板，距跑道南端约220 m（图1板A），平面尺寸5.0 m×5.0 m；道面结构自上而下为42 cm水泥砼面层、沥青基隔离层、40 cm水稳碎石基层以及压实土基；道面横缝为设传力杆假缝，纵缝为设传力杆平缝。道面于2020年4月浇筑完成，测试时已经历1次寒暑循环。道面未通航，仅承受零星车辆荷载。

1.2 传感器布设及数据采集

为监测道面温度响应，在板内埋设温度传感器和应变传感器。温度传感器采用拜安BA-OFT 10光纤光栅温度计，在板角处竖向分4层等间距埋设。应变传感器采用拜安BA-OFS15E光纤光栅应变计，在纵缝板边中点和板角、横缝板边中点和板角各选择1处，每处板顶、板底各埋设1支应变计。传感器埋设采用钢筋支架固定。传感器布设位置见图1。

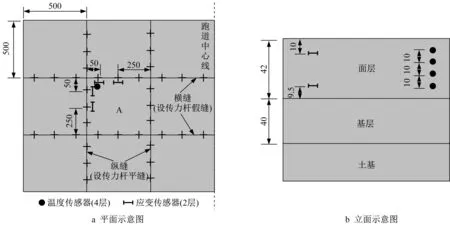
图1 道面传感器布设位置示意图（单位：cm）Fig.1 Layout of sensors in airport pavement slab（unit:cm）

传感器感知信号经光缆传输至室内采集仪，由拜安FT 210-16采集仪解调换算后输出所需物理量，换算参数由厂家提供。数据采集时间为2021年4月1日09：00—2021年4月4日08：30，数据采样频率为1次·（10 min）-1。测试期间气温12～18℃，天气状况为阴转多云。

1.3 弯沉测试

采用Carbrol车载落锤式弯沉仪（falling weight deflectometer，FWD）测试道面弯沉。其承载板半径15 cm，荷载脉冲时长0.03 s，设9个传感器（D1～D9），见图2a。荷载级位设为200 kN。测试位置选取板中、纵缝板边中点和板角、横缝板边中点和板角，见图2c；为测试接缝传荷能力，边、角位置需跨缝测试；同时，为比较接缝两侧加载弯沉差异，在板边和板角接缝两侧分别加载，见图2b。

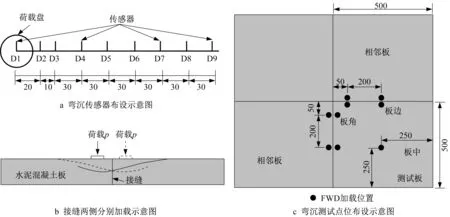
图2 弯沉传感器及FWD测试点位布设示意图（单位：cm）Fig.2 Layout of deflection sensors and FWD testing points（unit:cm）

2 数据分析

2.1 道面温度

由图3a可知，同一时刻，板内温度沿竖向呈非线性变化。图3b显示，板内不同深度温度按日周期性波动；波动幅度随深度增加而依次减小，相位也顺次滞后，各层相位差约为1 h。温度梯度（板顶与板底温度差/传感器距离）及平均温度同样呈日周期循环波动；正温度梯度在下午14：00—16：00之间达到极值，负温度梯度极值则一般出现在早晨07：00—08：00之间。

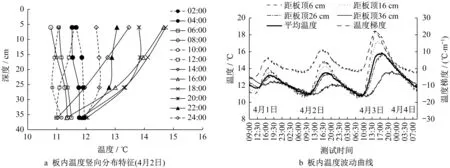
图3 道面板日温变化特征Fig.3 Daily temperature variation characteristics of concrete slab

2.2 应变

原始应变数据包含道面有效总应变和混凝土终凝时刻的原始总应变，原始总应变影响道面固化翘曲、干缩、徐变等长期形变分析，但对日周期应变波动规律影响不大。本试验未捕捉到原始总应变，取为0。

图4表明，各点不同深度应变呈周期约24 h的循环波动。白天多数时段上层应变高于下层，表明板体下层相比上层呈收缩趋势，道面中部拱起、四周下翘；夜间则相反。因而板内层间应变的相对大小差异是道面翘曲的根本原因。从相位上分析，各处上层应变均滞后于下层，相位差约为2～4 h。

图4 板内应变变化特征Fig.4 Strain variation characteristics of concrete slab

采用线性内插法获得应变计埋深的温度数据，以横缝板边中点为例分析板内应变随温度变化规律。由图5可知，板内应变随温度变化具有显著滞回特征，滞回曲线近似为椭圆。对比图4应变数据分析认为，滞回特征的直接成因是应变随温度变化存在相位差，相位差越大（小于6 h），滞回圈短轴越大；滞回特征的根本原因则可能是混凝土材料温度变形的滞后性。

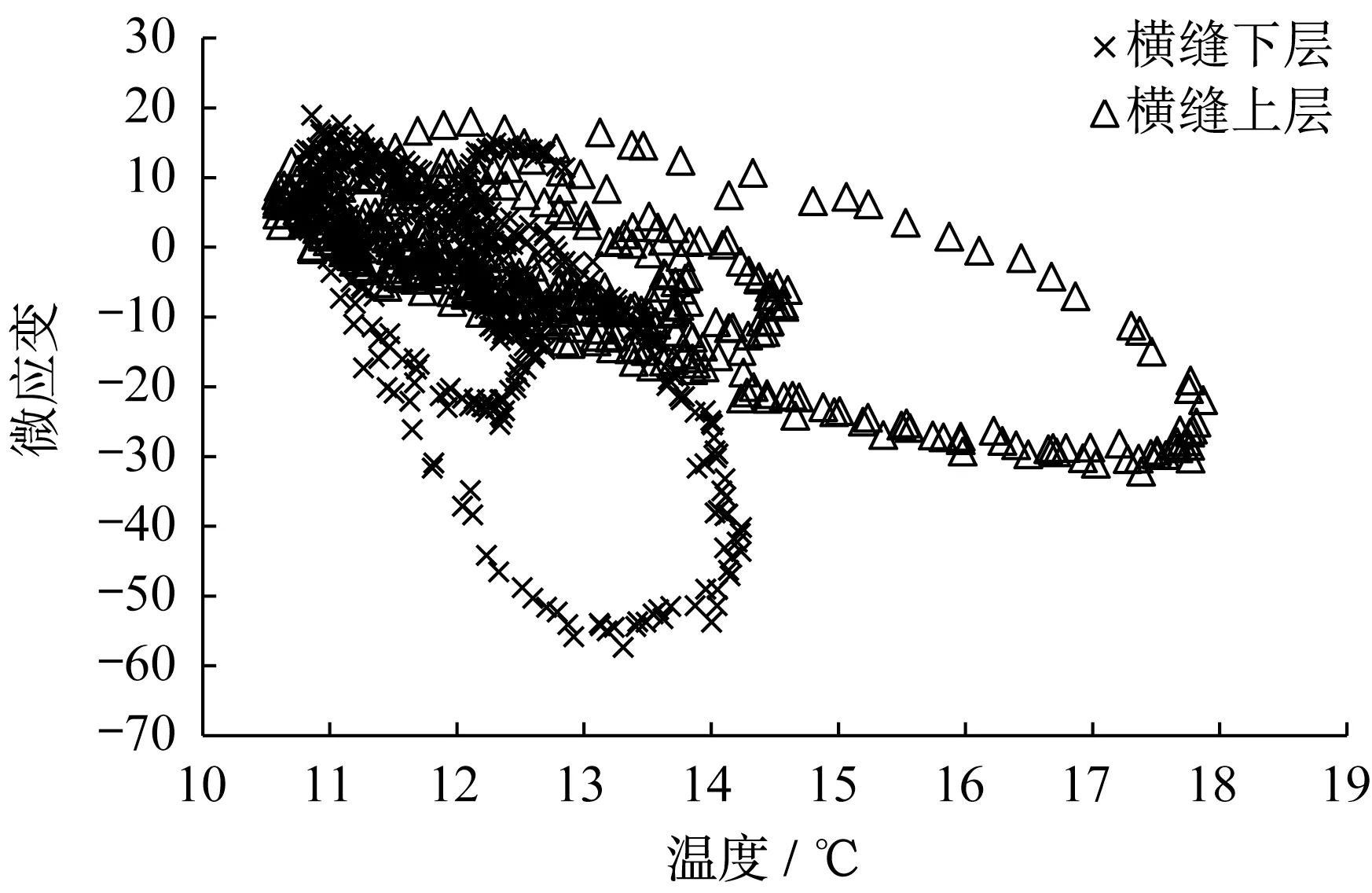
图5 板内应变-温度滞回特征（横缝板边中点）Fig.5 Hysteretic characteristic of strain versus temperature(midpoint of transverse joint)

2.3 道面曲率

道面板内竖向温度梯度的存在，导致道面板顶和板底的形变并不一致。在一定假定条件下，理论上可通过板顶和板底的应变推算道面翘曲曲率［19］：

式中：ρ为道面板翘曲曲率，m-1，正值为向上翘曲，负值为向下翘曲，ρ绝对值越大道面板翘曲越显著；εt、εb分别为板顶应变和板底应变；D为板顶与板底应变计间距，m。

按式（1）计算不同接缝类型板边、板角的翘曲曲率。图6显示，道面曲率基本在正温度梯度时为负，负温度梯度时为正；且温度梯度绝对值越大，ρ绝对值越大；每日14：00—16：00左右道面向上翘曲最为显著，每日06：00—07：00左右道面向下翘曲最为显著。假定道面翘曲后呈球面，计算各点翘曲量（负值为向下翘曲）。板边位置，纵缝（设传力杆平缝）翘曲量为-0.836～0.322 mm、横缝（设传力杆假缝）翘曲量为-0.480～0.127 mm；板角位置，纵缝翘曲量为-3.517～1.143 mm、横缝则为-3.428～0.892 mm；由此可知，板角翘曲比板边更为显著，且接缝为设传力杆平缝时，道面翘曲量更大。道面板温度翘曲导致面层与基层间形成脱空，其日周期循环变化的特征对刚性道面性能评价造成极大影响［16］。

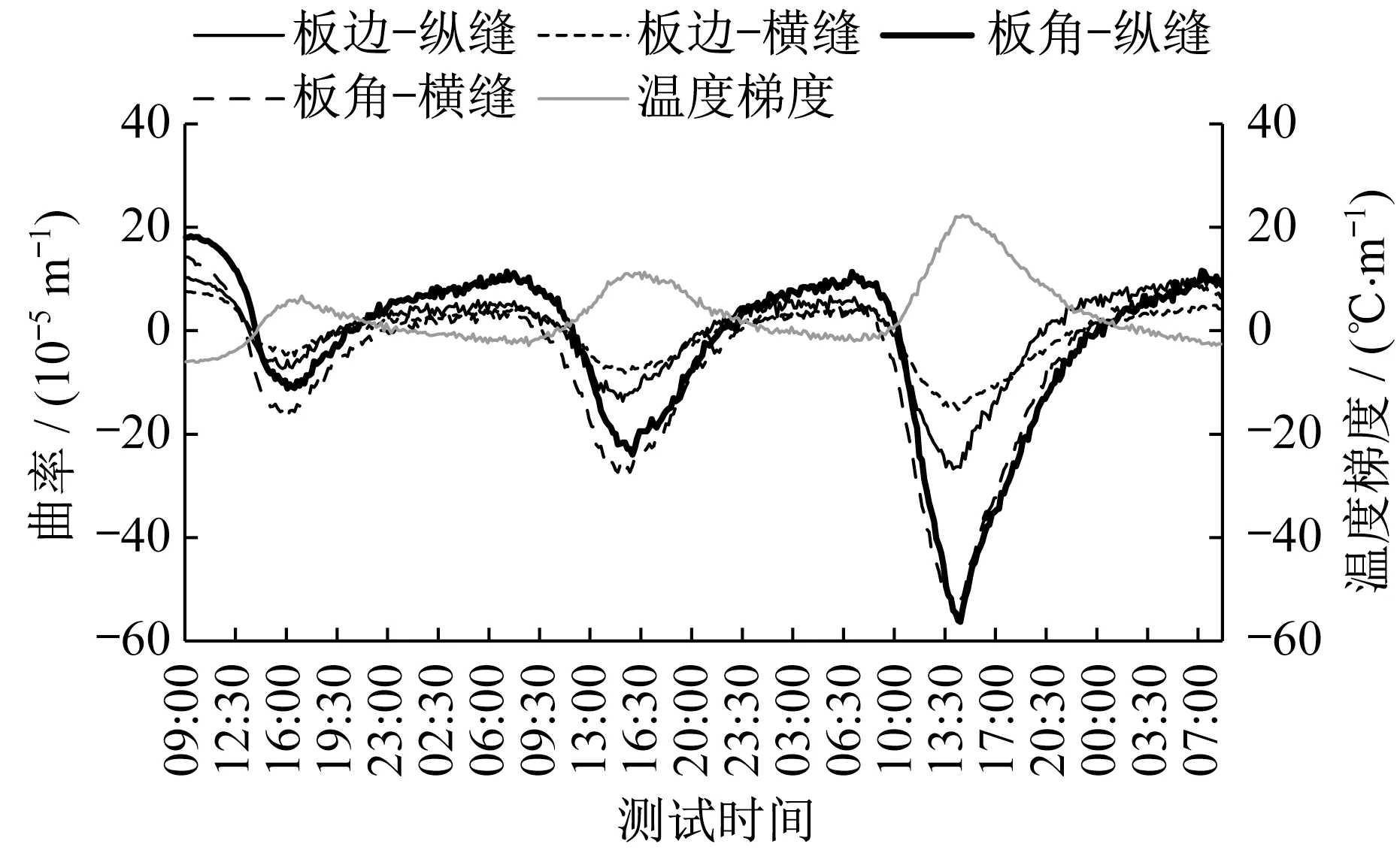
图6 道面曲率随温度梯度波动曲线Fig.6 Curve of pavement curvature fluctuation with temperature gradient

图7结果显示，道面曲率-温度梯度曲线同样呈现一定滞回特征，但相比温度-应变滞回曲线，由于板顶与板底应变差和温度差的相位差更小，其滞回特征更不明显。因此，分析道面曲率-温度梯度间相关关系能更好地反映道面板温度效应下的形变特征。

以一次方程y=-ax+b的形式拟合道面曲率与温度梯度间的关系式，如表1所示。

由表1可知，各曲线拟合系数R2均值达到0.8以上，表明道面曲率变化80%以上由温度梯度所致。各点4月1日至4月3日3 d内a的拟合结果稳定；据其物理意义结合曲率理论计算式［20］可知，a即为水泥砼热膨胀系数，其拟合结果均值为（0.87～2.43）×10-5。各点a值差异反应了各点道面板翘曲受约束程度不同；a越小，表明受约束程度越高；这与前述翘曲量计算反映的结论一致。此外，图7及表1显示，温度梯度为0时，道面曲率并不为0，可能是道面板固化温度梯度影响了道面实际的翘曲形态［21］。

表1 道面曲率与温度梯度间关系拟合结果Tab.1 Fitting results of trelationship between pavement curvature and temperature gradient

图7 道面板曲率-温度梯度滞回曲线Fig.7 Hysteresis loop of slab curvature versus temperature gradient

2.4 道面弯沉及弯沉指标

2.4.1 弯沉值

图8为同板板中、板边及板角处弯沉（下文如无特别说明，均为同板弯沉）随温度梯度变化曲线。由图8可知，随着温度梯度变化，板中弯沉基本稳定（变异系数仅4.9%）；板边和板角弯沉均随正温度梯度增大而减小，随负温度梯度增大而增大。横缝处（设传力杆假缝），板边弯沉变异系数为4.3%，板角弯沉变异系数为14.2%；纵缝处（设传力杆平缝），板边弯沉变异系数为7.0%，板角弯沉变异系数则达到15.2%。表明温度翘曲对板角弯沉影响程度更大，且设传力杆平缝道面弯沉更易受温度翘曲影响。

图8 道面最大弯沉和温度梯度日变化曲线Fig.8 Daily variation curve of maximum deflections and temperature gradient

2.4.2 接缝传荷系数

接缝传荷系数（load transfer efficiency）以板边接缝两侧未受荷板弯沉与受荷板弯沉之比表征，即

式中：ELT为接缝传荷系数；DLoad、DUnload分别为受荷板和未受荷板弯沉，即图2a中D2、D3读数，μm。

图9表明，24 h之内，设传力杆假缝道面ELT极大值与极小值仅相差4.4%，基本无变化；而设传力杆平缝道面ELT波动较大，白天下午时段显著高于其他时段，绝对值变化幅度达到12.9%。这表明平缝类道面的接缝传荷能力更易受温度变化影响。

图9 接缝传荷系数日变化Fig.9 Daily variation of load transfer efficiency

温度对接缝传荷能力的影响分为两方面：一方面是由于道面平均温度变化（胀缩）导致接缝张开或闭合，影响接缝传荷能力；另一方面是由于道面竖向温度梯度变化（翘曲），接缝截面转动改变接触条件，影响接缝传荷能力。目前，季节性平均温度变化对接缝传荷能力影响的研究较多，而日周期温度变化条件下，平均温度和温度梯度对接缝传荷能力的影响差异并不明朗［22］。

以ELT变化较大的设传力杆平缝为例，分析平均温度和温度梯度对ELT的影响。从图10可知，ELT随道面平均温度升高而增大，随温度梯度增大而增大；以一次函数拟合ELT与二者关系，道面平均温度、温度梯度与ELT之间拟合系数R2分别为0.65、0.86，温度梯度与ELT之间相关性更好；这表明，日周期内道面接缝传荷能力波动更受温度梯度变化影响。

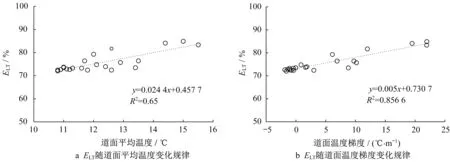
图10 E LT随道面温度变化规律Fig.10 E LT versus pavement temperature

2.4.3 弯沉比

我国《民用机场道面评价管理技术规范》（MH/T 5024—2019）采用弯沉比法判定道面板底脱空，即以“板边或板角荷载中心弯沉/板中荷载中心弯沉”作为脱空判定值，并根据不同接缝传荷等级选取相应判定标准。由前述分析可知，道面边、角弯沉受温度变化影响显著，而板中弯沉则基本稳定；因此，基于弯沉比进行板底脱空判定时必然受到温度变化的影响。

以纵缝处为例（图11），板边和板角的弯沉比均随正温度梯度增大而减小，随负温度梯度增大而增大；24 h之内，原位测试的板边和板角弯沉比变异系数分别为8.15%、16.17%。道面温度变化对弯沉比的这种影响可导致板底脱空的误判［18］。

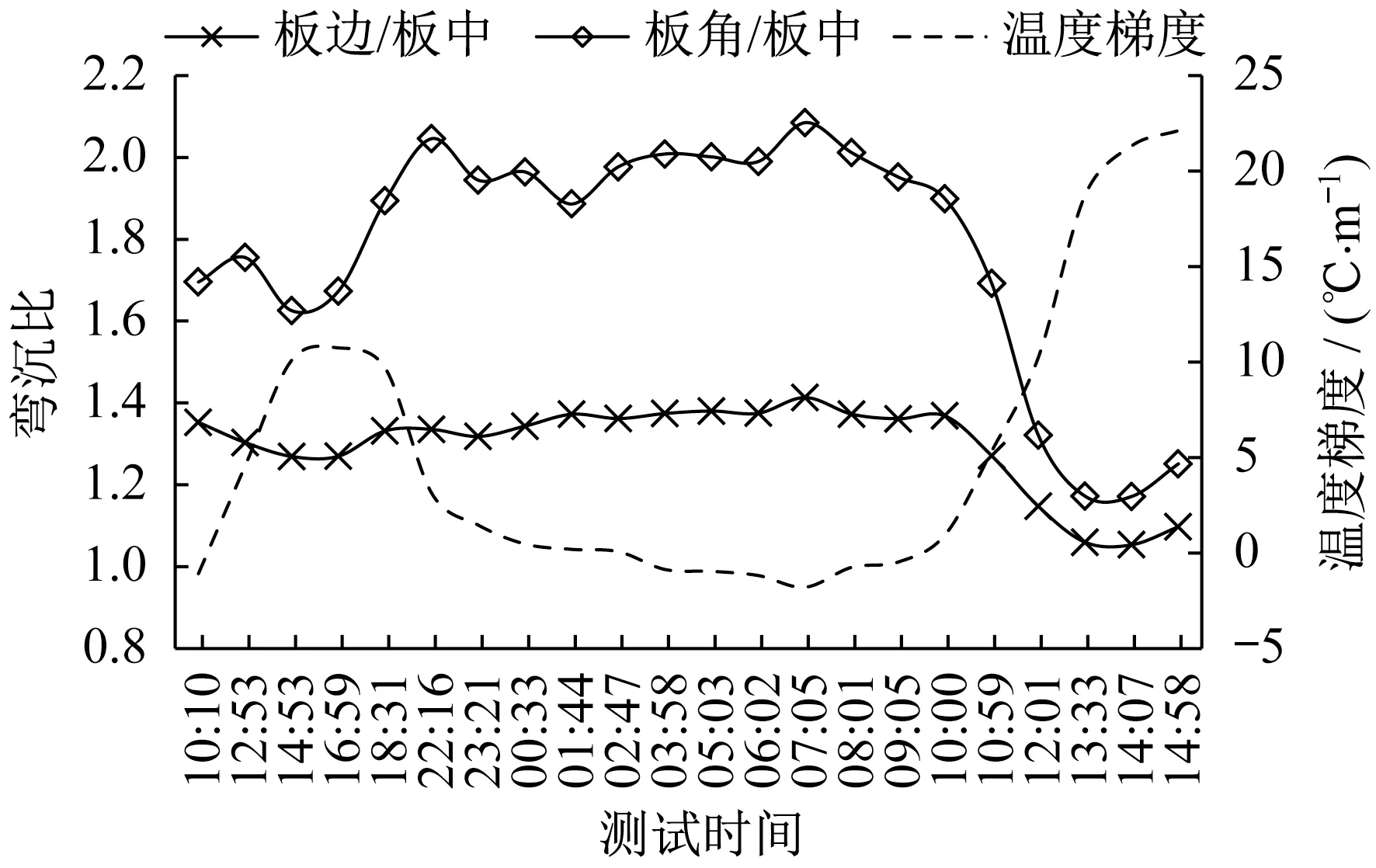
图11 弯沉比与温度梯度日变化曲线（纵缝）Fig.11 Daily variation curve of deflection ratio and temperature gradient

2.4.4 接缝两侧弯沉之和

接缝两侧弯沉之和（sum of deflections on two sides of joints）是刚性道面性能评价中的一项指标。其计算式如下：

式中：DS为接缝两侧弯沉之和，μm。

由于道面接缝截面的竖向不均匀性，在接缝两侧分别加载可获得同一接缝的不同接缝传荷能力。因此，通过在接缝两侧分别加载以及24 h原位监测的方式，可获得不同接缝传荷能力条件下的DS，以及不同温度条件下的DS。进而可分析接缝传荷能力和温度对DS的影响。从图12可知，当ELT不变时，DS也无变化（横缝板边、纵缝板边及横缝板角）；而当ELT存在较大差异时，DS仍然稳定（纵向板角）；表明DS与接缝传荷能力之间可能存在相互独立的关系。

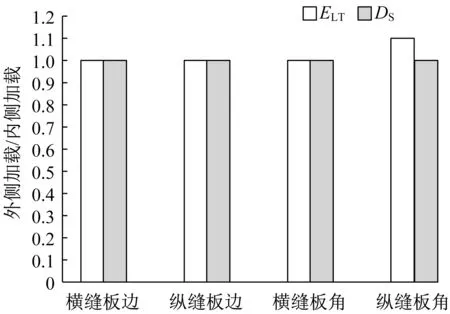
图12 D S与E LT变化对比Fig.12 Comparison of variation of D S and E LT

以零温度梯度时刻（本文为03：00）弯沉值为基准，计算不同温度梯度下DS的变化值ΔDS，分析温度梯度与DS的关系。图13表明，DS随着温度梯度增加而减小。二次函数拟合结果显示，板边及板角的ΔDS与温度梯度之间拟合系数R2均达到0.84以上；结合前述测试结果认为，DS能够在较好地避免接缝传荷影响的同时反映道面温度翘曲程度。

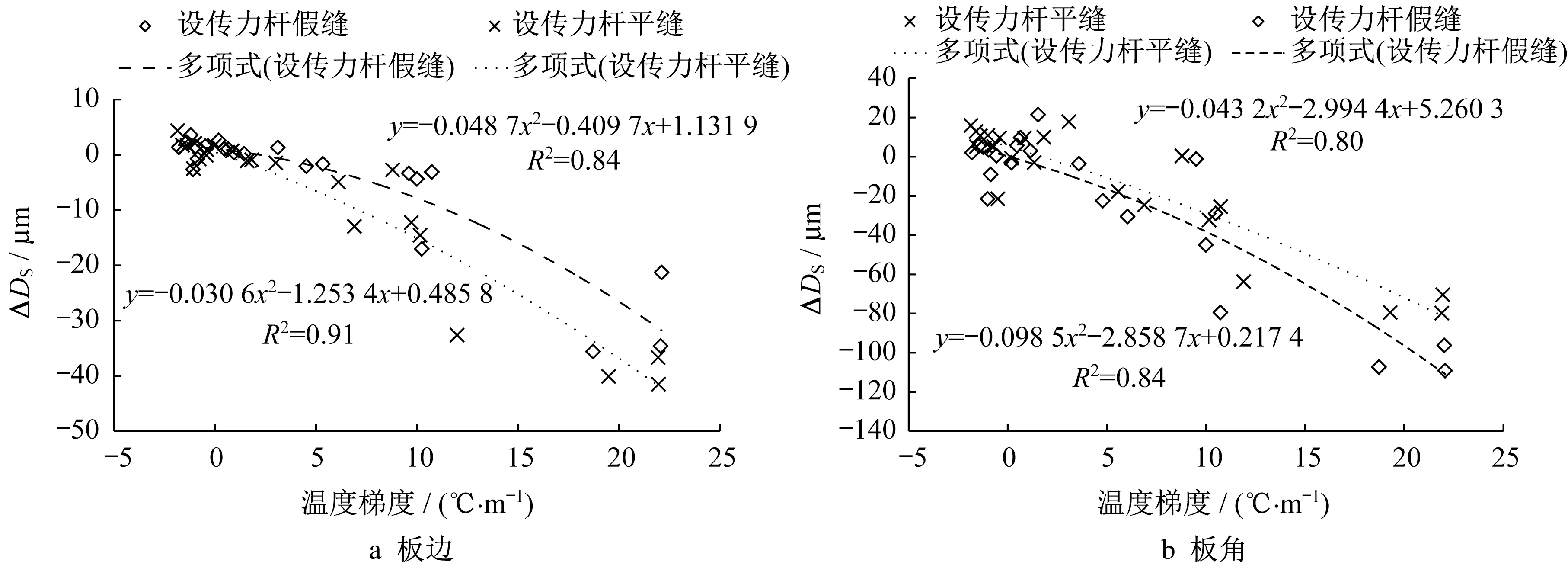
图13 D S与温度梯度间关系Fig.13 Relationship between D S and temperature gradient

3 讨论与建议

数据分析结果显示，水泥道面日周期温度效应对机场水泥道面性能评价影响显著，尤其影响板底脱空评价结果。温度对机场水泥道面板底脱空评价的影响主要体现在：①温度梯度导致道面发生温度翘曲脱空，且随日周期温度变化反复出现和恢复，是一种“假脱空”，虽然在实际工程中无需处治，但会干扰真正需要处治的唧泥脱空判别。②既有机场水泥道面板底脱空判定标准是基于不同接缝传荷能力水平选定，而温度变化影响接缝传荷能力测试结果。因此，为实现机场水泥道面的精准评价与养护，在进行道面板底脱空评价时应考虑温度影响。

目前主流的道面板底脱空判定仍基于弯沉检测，如需考虑温度影响进行板底脱空判定，其重点与难点仍在于如何区分接缝传荷和板底脱空对弯沉的影响［23］。采用既有方法判定机场水泥道面板底脱空时，由于不同脱空条件下获得的接缝传荷系数并不相同［24］，接缝传荷评价和板底脱空评价二者的耦合作用可能会导致结果的误判。而此次试验发现，DS与温度梯度之间存在较高的相关性，且DS可能与接缝传荷系数相互独立。DS的上述特征表明其在考虑温度影响进行水泥道面板底脱空时具有一定优势，未来可考虑对DS的相关特征展开进一步研究，以期实现温度影响条件下水泥道面板底脱空的精准识别。

4 结论

（1）道面板内温度、平均温度均呈日周期性波动；温度沿深度方向传递的滞后性特点导致板内形成竖向温度梯度；温度梯度同样呈周期性波动，正、负温度梯度分别在14：00—16：00和07：00—08：00达到极值。

（2）日周期内，道面板内应变循环波动，且应变随温度变化呈现一定滞回特征；二者相位差是导致曲线滞回特征的直接成因，根本原因则可能在于混凝土材料温度变形的滞后性。

（3）道面曲率随日周期温度变化呈现周期性波动，白天板体中部拱起、四周下翘，夜间则相反。板角翘曲大于板边，接缝类型差异对道面板边位置翘曲影响较大，对板角位置则基本无影响。道面曲率-温度梯度曲线滞回特征较弱，能较好地反映道面板温度效应下的形变特征。

（4）日周期温度变化条件下，道面边、角弯沉及板底脱空判定值均随正温度梯度增大而减小，随负温度梯度增大而增大；道面板中弯沉则基本不受温度变化影响；接缝传荷系数波动更多受温度梯度变化影响。

（5）接缝两侧弯沉之和DS与温度梯度之间存在良好相关性，且DS可能与接缝传荷能力无关；表明DS在考虑温度影响进行水泥道面板底脱空判定时具有一定优势，建议对其特征展开进一步研究，以实现水泥道面板底脱空的精准识别。