Elastic electron scattering with CH2Br2 and CCl2Br2:The role of the polarization effects

Xiaoli Zhao(赵小利) and Kedong Wang(王克栋)

1School of Science and Technology for Opto-electronic Information,Yantai University,Yantai 264005,China

2School of Physics,Henan Normal University,Xinxiang 453007,China

Keywords: electron scattering,elastic cross section,shape resonance

1. Introduction

Electron–molecule collisions are of fundamental importance and have many applications ranging from purely scientific(e.g.,physic-chemistry of interstellar and environmental media) to industrial uses (plasma-based processing, energy conversion).Study of low-energy electron collisions with biomolecules is motivated by their importance in the understanding of radiation damage,particularly of DNA.[1]Despite a growing demand for electron-assisted data (cross sections,transport coefficients) the accurate simulation of electron–molecule scattering at low energies still remains a computational challenge. One of the difficulties for theoretical calculations is how to accurately describe the polarization between the scattering electron and the target. At low energies, only the elastic channel is electronically open and the distortion of the electronic cloud is taken into account by allowing virtual excitations from the ground state. This effect combined with the proper solution of the scattering problem,including the exchange interaction,is known as static-exchange plus polarization(SEP)approximation.Several methods were developed to solve electron–molecule scattering problems,and theR-matrix method is one of them.[2,3]In theR-matrix method, the SEP model uses singlet excitations out of the Hartree–Fock (HF)wave function to represent target polarization effects,and will give rise to the important questions: (i)how many of the virtual orbitals must be included in a calculation in order to provide a reliable cross section and an accurate resonant parameter? (ii) how many of valence orbitals are allowed to form two-particle-one-hole states to describe the polarization? (iii)how do these virtual orbitals and valence orbitals(to form twoparticle-one-hole states) affect the elastic cross section? (iv)how to obtain the convergence cross section. Recently, theoretical groups[4–11]have addressed some of these issues using different methods to describe the electronic excitation states,at specific levels of multichannel coupling. It was pointed out that many challenges have to be overcome to obtain reliable cross section. When employing theR-matrix approach at the SEP level,several groups[12,13]studied the convergence of integral cross sections and shown the dependence on polarization effects as a function of the number of virtual orbitals.These calculations, however, were limited to discuss the influence from the virtual orbitals, and no discussion of the influence from the valence orbitals was given.

In this work, we present a comprehensive study of electron collisions with dibromomethane (CH2Br2) and dichlorodibromomethane(CCl2Br2)molecules for energies up to 20 eV by using theR-matrix method. CH2Br2and CCl2Br2can be decomposed by solar ultraviolet radiation in the upper atmosphere to release atomic bromine or fluorine, which can react with stratosphere ozone layer and destroy it.[14]Collision of low-energy with halomethane is a primary step in plasmaprocessing chemistry and may play a role in the chemistry of the atmosphere. We performed systematic calculations to look for an improvement in the description of the polarization effects. Our aim is to investigate the resonant spectra presented in the elastic cross sections and to discuss how the inclusion of polarization affects resonances and cross sections. The rest of this paper is organized as follows.In Section 2 we highlight some relevant points of the theoretical method and present the computational procedure for the calculation. In Section 3,we present the results and our discussion. Finally, In Section 4,we also present a brief summary of our results.

2. Computational details

We use the UK molecularR-matrix code to carry out the scattering calculations. This method has been described carefully elsewhere,[2,3]thus here we just present some relevant details. Within theR-matrix method, configuration space is divided into an inner and an outer regions. The inner region is defined inside a sphere of radiusr=13a0which completely contains theN-electron wave function of the target. This region is where the complicated physics occurs because allN+1 electrons interact strongly so that both exchange and correlation effects must be taken into account. TheR-matrix method represents theN+1 electrons wave function using a closecoupling approximation which can be written as follows:

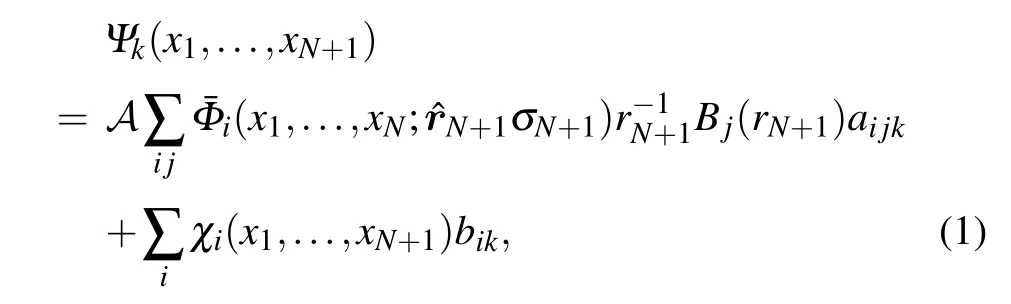
here the ¯Φidenotes the channel functions constructed from theN-electron target state,andAis an antisymmetrization operator.xNis the spatial and spin coordinate of theNth electron.Bj(r) represents the continuum orbital. Theχiis additional(N+1)-electron bound states. Coefficientsaijkandbikare variational parameters determined as a result of the matrix diagonalization. The sum in the second term of Eq. (1)represents the short-range correlation and polarization effects,running over all configurations for (N+1) electrons that areL2functions. In the inner region,the continuum orbitals were constructed using Gaussian-type orbitals(GTO)[15]for which we used up tolmax=4.

In the outer region, a one-particle wave function represents the continuum electron which moves in a local longrange potential. In this region, the scattering electron is distinguishable from the target electrons,and both exchange and correlation are neglected. The inner region data on the boundary is used to solve the outer region problem. Matching the asymptotic solutions to know expressions, theK-matrix,Smatrix, resonant parameters and cross sections can be determined.

Scattering calculations were performed in SEP and closecoupling (CC) approximations. For the SEP calculation,we include the ground state wavefunction in expansion (1),andN+1 configurations involving single excitation from the ground state are used to describe close-range correlationpolarization effects. TheL2functions take the form

where the core orbitals of the molecule are always doubly occupied byNcelectrons and the molecule is allowed to polarize by promoting one electron from the valence space to the selected number of virtual orbitals,which are also available for the scattering electron. The SEP approximation as described can give the good resonance parameters for shape resonances and can also reveal core-excited resonances associated with single excitations of the target molecule. But it is probably necessary to perform close-coupling calculations to obtain reliable parameters for the Feshbach resonances. In order to check the stability of our calculations and influence of virtual orbitals(VOs)and active electrons(AEs),we performed several SEP calculations at four different levels for each molecule.In the case of CH2Br2,the number of VOs open for target excitations is 31 and 39(this is the largest one for HF/cc-pVDZ calculation). For CCl2Br2,the number of VOs open for target excitations is 40 and 48. We allow one electron from a different number of occupied valence orbitals(OVO)to excite and form holes. The number of active electrons we used is 8, 12,and 16 for CH2Br2and 12, 16, and 20 for CCl2Br2. Table 1 summarizes the number of VOs and AEs used in four different SEP models for each molecule.

Table 1. The number of molecular orbital and active electronsemployed in the SEP model for each molecule.

In the CC model,the target can be electronically excited and a number of states are included in expansion(1).Inclusion of excited states describes some of the polarization effects,but for targets with high polarizability,additionalL2functions must be included. TheL2functions take the form

The calculations were performed at the ground state equilibrium geometry. The molecule geometries were taken from CCCBDB database[16]at the B3LYP/6-31+G**level.The relativistic effect is not considered in the present paper. The data of their equilibrium geometries is given in Table 2. The calculated dipole moment for CH2Br2is 1.75 D in the SEP model and 1.68 D in the CC model,which is comparable to the experimental values of 1.43 D,[16]although our results are overestimated. Our predicted dipole moment for CCl2Br2is 2.49 D in SEP model and 2.44 D in CC model. There is no available dipole moment of CCl2Br2for comparison.When the electron energy is low,the long-range dipole potential becomes important,inducing a systematic enhancement of the cross sections.This effect is usually taken into account with a Born-closure procedure.[17]In the present work,we focus on the discussion of the polarization effects on the resonance and cross section,and then our cross sections are not corrected for this effect.

Table 2. Equilibrium geometry data used for ground state of CH2Br2 and CCl2Br2. Distances in ˚A and angles in degrees.

3. Results and discussion

In Fig. 1 we show integral cross sections (ICSs) for CH2Br2and CCl2Br2. The cross sections were obtained in different SEP approximations and CC 1 state approximation for energies up to 20 eV. All models yield similar results for electron energies above 0.5 eV for CH2Br2and above 1.5 eV for CCl2Br2. For very low scattering energies, however, the predictions differ considerably and there are pronounced structures in the cross sections,which are signatures of shape resonances. The cross sections in the low-energy region are more sensitive to the polarization than these in the high-energy region. This is the main reason why differences in the lower region are bigger than in the higher region. Unfortunately,there is no experimental elastic cross-section data available for comparison. For the purpose of investigating the nature of related resonances and to assign them to the corresponding symmetries of theC2Vgroup, we calculated the symmetry decomposition of ICSs in SEP and CC 1 state models. The results are shown in Figs. 2 and 3 for CH2Br2and CCl2Br2, respectively. Resonances are usually judged by two points. One is that their cross sections show enhancements in the vicinity of a resonance.The other one is that the eigenphase sum changes by a factor of aboutπradians in the relatively narrow energy range.Here we obtained the position of a resonance according to the eigenphase sum.The obtained positions and symmetries of resonances are summarized in Table 3.

Table 3. Position of the resonances (eV), obtained in four different SEP models and CC1 state model. The available experimental and MS-Xα results are also shown for comparison.

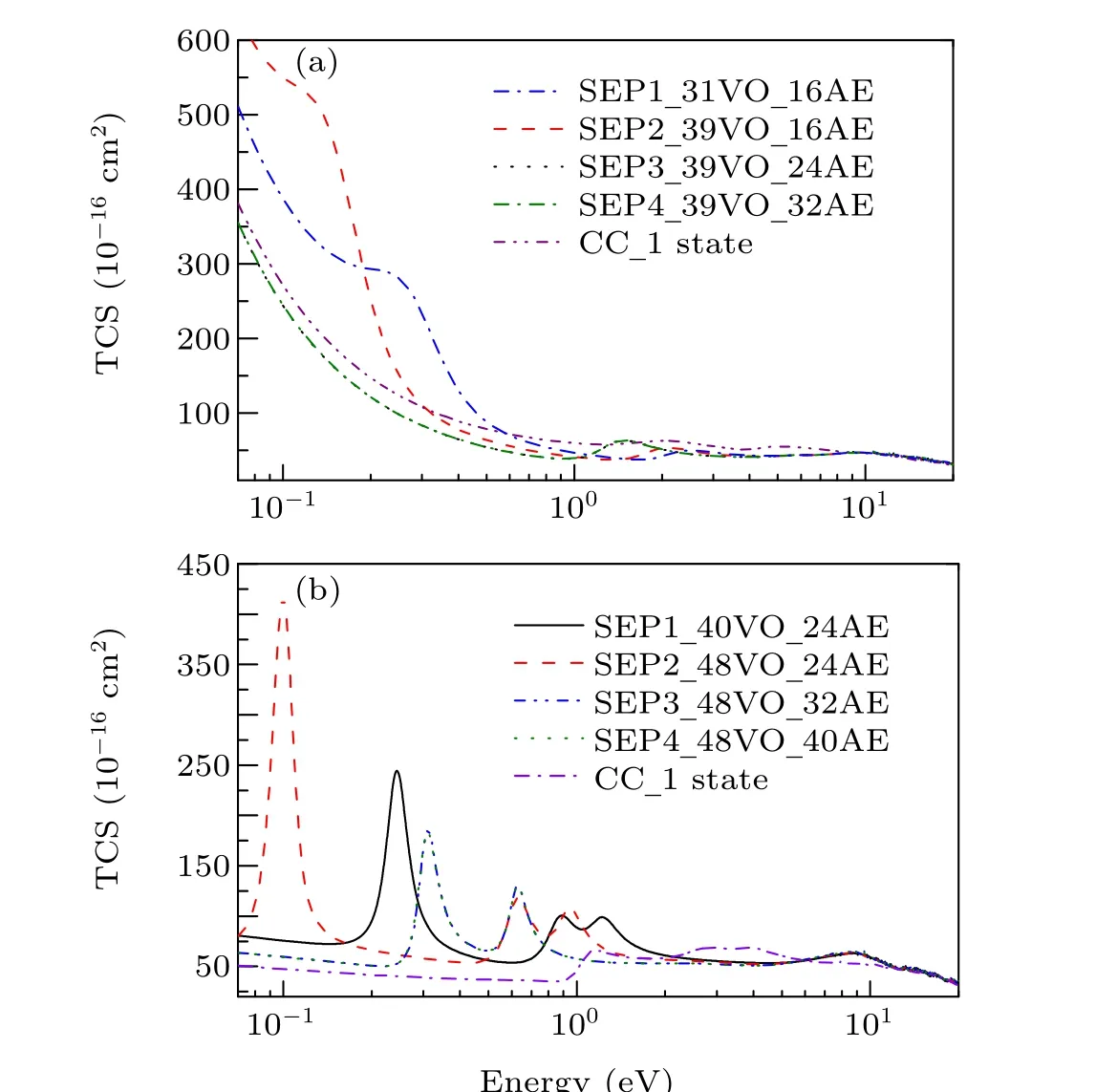
Fig. 1. Integral elastic cross section for (a) dibromomethane and (b)dichlorodibromomethane obtained in different SEP approximations and CC 1 state approximation.

Fig.2. Symmetry decomposition of the elastic integral elastic cross section for electron collision with dibromomethane in four different SEP approximations and CC 1 state approximation.

The electron transmission spectrum reported by Modelliet al.[18]suggested a single structure (σ2∗resonance) at 1.93 eV for CH2Br2which they assigned to a shape resonance with a C(2p)character. The position of theσ2∗resonance was estimated at 1.68 eV from multiple scattering (MS)-Xαand at 1.88 eV from continuum multiple scattering(CMS)-Xα.[18]Compared with the ETS data, our calculated position ofσ2∗resonance in CC 1 state and SEP1 models is too high in energy, and that in the SEP2 model is slightly high and shows relatively good agreement. In order to improve the position of the resonance it is necessary to consider more VOs and AEs in describing the polarization effects in SEP calculations. We have used the largest number of the VOs within HF/cc-pVDZ wave function in the SEP2 model. And then we performed the SEP3 calculation including 12 OVOs and theσ2∗resonance moves to 1.61 eV.It should be noted that SEP1 and SEP2 predict a low-lyingσ∗resonance at 0.27 eV and 0.14 eV,respec-1tively,which are in good agreement with the value of 0.20 eV at MS-Xαlevel. This resonant peak was not observed in the ETS because it shows the sharp increases at the smaller energies. All the present models predict a broad high-lyingπ∗resonance located at 6.74–7.36 eV.Thisπ∗resonance is possibly too broad to be detected in the measurement.

Results for the symmetry decomposition of elastic cross section for electron scattering from the ground state of CCl2Br2are presented in Fig. 3. All models predict twoσ∗resonances which are signatures of shape resonances. They are observed at 1.22 eV and 4.32 eV in the CC 1 state model,at 0.88 eV and 1.24 eV in the SEP1 model, at 0.63 eV and 0.95 eV in the SEP2 model, at 0.32 eV and 0.63 eV in the SEP3 model and at 0.32 eV and 0.63 eV in the SEP4 model.Clearly, with increasing the VOs and active electrons in the SEP calculation,the positions of these two resonant peaks decrease. The retention of a large number of VOs and active electrons in the SEP model provides the necessary polarization potential in anab initioway,which is crucial for determining the resonances and their resonance parameters. It should be noted that almost no differences observed between the elastic cross sections of SEP3 and SEP4 calculations indicate the convergence of SEP results of the present 32 AEs calculation.There is also aπ∗resonance detected at 6.48 eV in CC 1 state model,at 0.24 eV in the SEP1 model,and 0.09 eV in the SEP2 model. The position of theπ∗resonance decreases with increasing the polarization in the calculations, and becomes a bound state in both SEP3 and SEP4 models. It is noted that resonances of B1in CC 1 state model are not clearly in Figs.2 and 3, and we judged from their eigenphase sum. The small peaks in higher energy region in these fgiures are nonphysical resonances which are related with pseudostates.

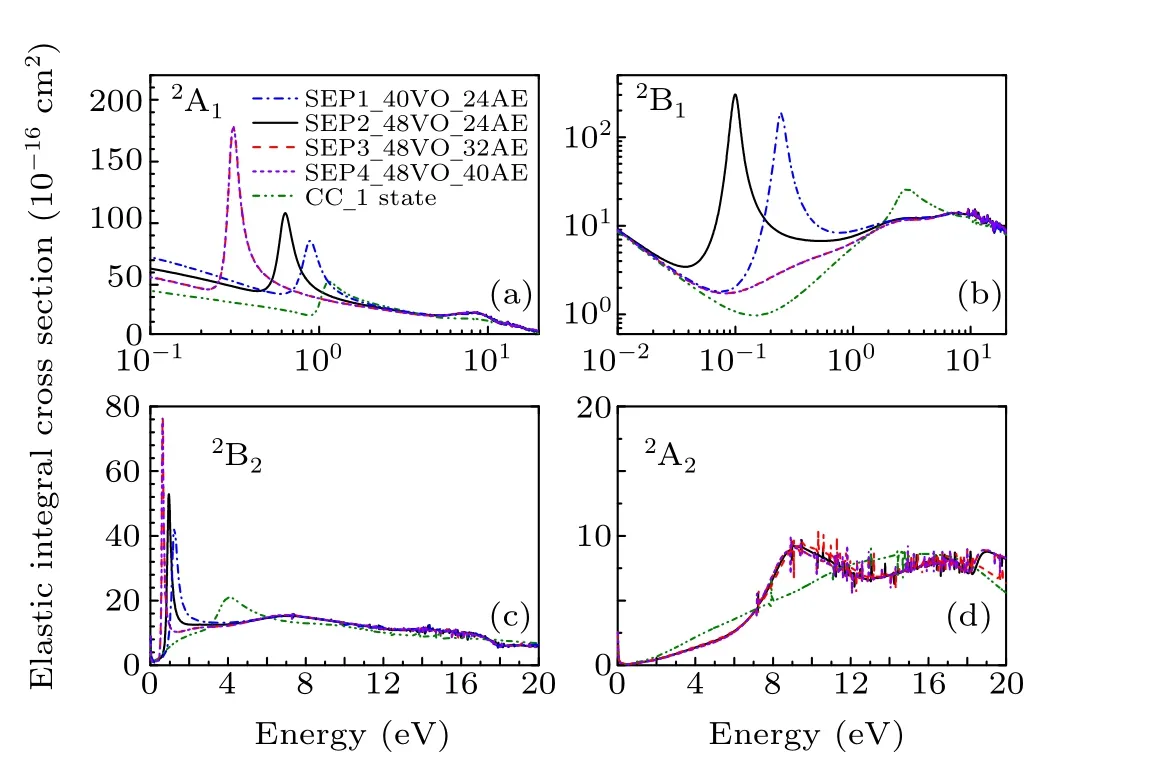
Fig.3. Symmetry decomposition of the elastic integral elastic cross section for electron collision with dibromomethane in four different SEP approximations and CC 1 state approximation.

Olthoffet al.[19]measured the electron transmission spectrum of CCl2Br2, and observed twoσ∗shape resonances at 0.4 eV and 1.0 eV,respectively. They also measured the yield of negative fragments using the DEA spectroscopy. Energies of maxima for Cl−and Br−production due to dissociative attachment are indicated at about 0.3 eV and 0.7 eV, respectively, which are in agreement with their ETS results. They noted that the electron transmission resonance near 1.0 eV must be due to electron capture in aσ∗2orbital with predominantly the C–Cl character, and the lower energy resonance must be due primarily to electron capture into aσ∗1orbital of the C–Br character. The calculated position ofσ∗2resonance in the SEP2 model is in good agreement with ETS data. The calculated position ofσ∗1resonance is above the experimental data. In order to improve the position of this resonance, we performed SEP3 calculation to include more AEs in the scattering calculation. Theσ∗1resonance moves down to 0.32 eV,in better agreement with the ETS data of 0.40 eV.[19]However,since we used the same polarization for each symmetry,this leads to the overcorrelation ofσ∗2, which located at the lower position in energy at 0.63 eV in SEP3 calculation. This also leads to the overcorrelation ofπ∗,which becomes a bound state.

The evaluation of differential cross section (DCS) is a stringent test for any scattering theory. In the present work,theK-matrix from four SEP models and the CC 1 state model are used to calculate DCSs following the procedure implemented in the program POLYDCS.[20]Figures 4 and 5 show the DCSs at 1 eV, 3 ev, 6 eV, 10 eV, 15 eV, and 20 eV for CH2Br2and CCl2Br2. There is no experimental data or other theoretical results at those energies for comparison. As shown in Fig. 4, obvious differences are seen among the results of different models for CH2Br2for the energies of 1 eV,indicating that polarization effect is important at lower energies. The results demonstrate that it is necessary for more VO and active electrons to be included in the SEP calculations to obtain the convergent elastic DCS for lower energy. With increasing the incident energy,polarization becomes less important,and as a consequence the SEP and CC results become similar.We have used 32 active electrons and the maximum number of VOs in the SEP4 model. Then we perform another SEP calculation to take 40 active electrons into account and obtain almost the same cross sections as SEP4. The result is not shown in the present paper. This provides a strong indication that a good convergence has been achieved to the elastic channel for SEP4 results in the energy region below 20 eV.It is noted that there are many Rydberg states existing for both molecules. These Rydberg states can affect the core-excited resonances and have no effect on shape resonances and elastic scattering cross sections.

Figure 5 shows the DCSs at 1 eV,3 ev,6 eV,10 eV,15 eV,and 20 eV for CCl2Br2molecule. Like CH2Br2,in the case of 1 eV,CC 1 state, SEP1, SEP2, and SEP3 models predict different DCS,which means that DCS is sensitive to the polarization in the low-energy region. As the energy is increasing,all SEP results show almost the same DCS.It is noted that SEP4 DCS is coincident with SEP3 result at all the impact energy studied here,supporting that good convergence of SEP3 DCSs has been obtained. For impact energy of 15 eV,the agreement between DCSs of the four SEP models and CC 1 state model shows that polarization is not important. For other energies,the presence of polarization in SEP models changes substantially the DCS,comparing to the one obtained at a CC 1 state calculation.

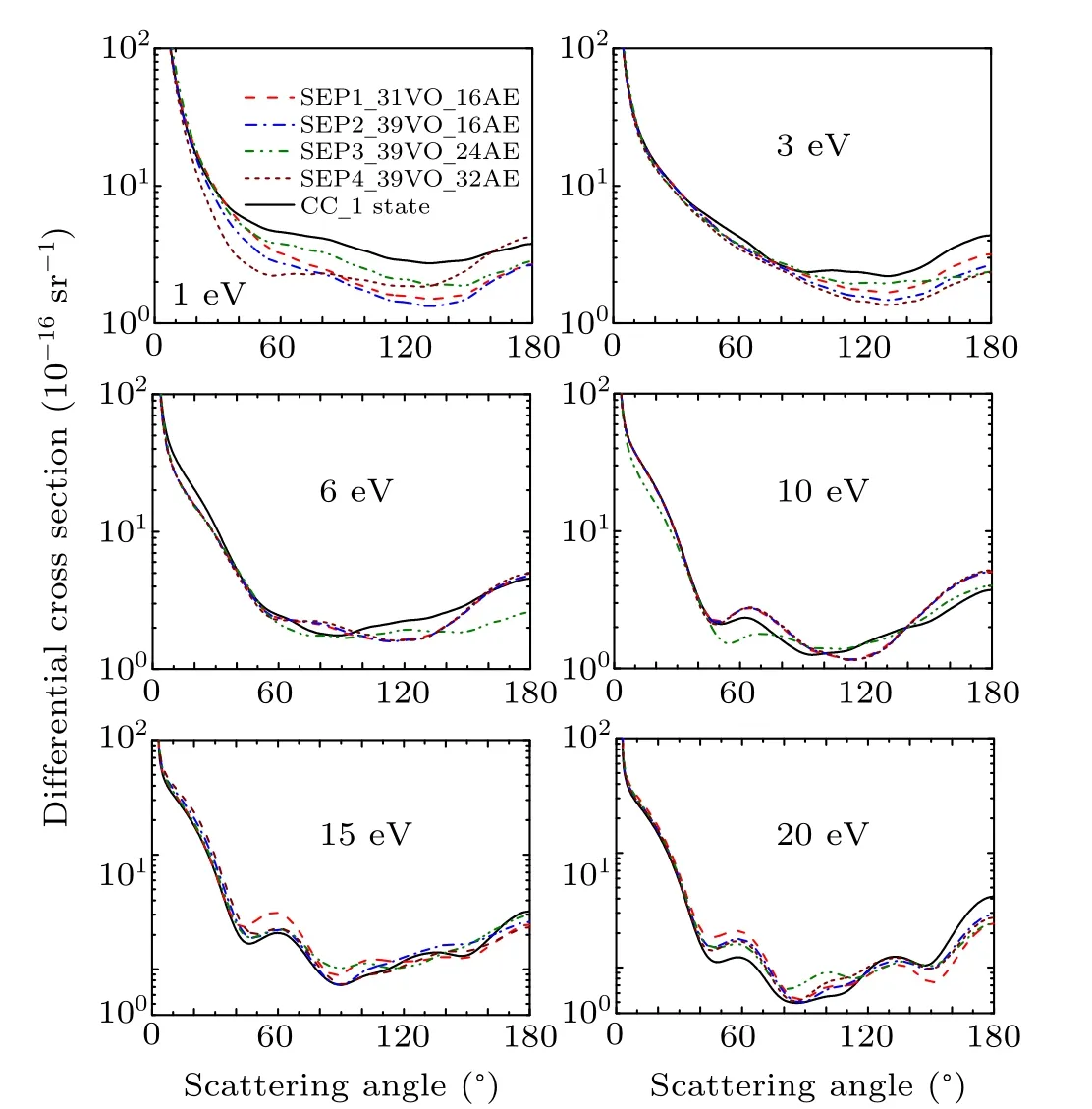
Fig. 4. Differential elastic cross section for dibromomethane at 1 eV, 3 eV,6 eV,10 eV,15 eV,and 20 eV in four different SEP approximations and CC1 state approximation.

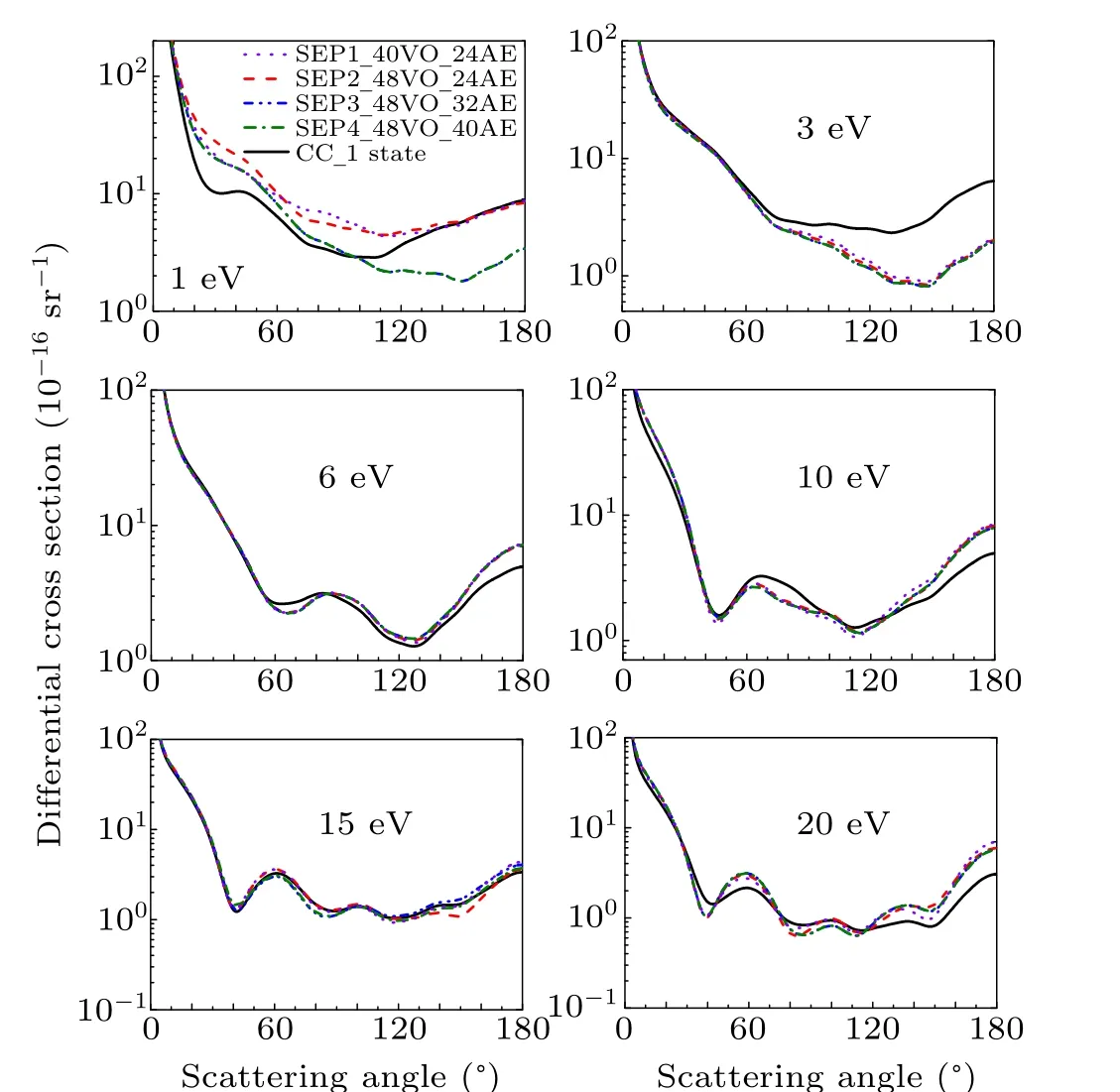
Fig.5. Differential elastic cross section for dichlorodibromomethane at 1 eV,3 eV,6 eV,10 eV,15 eV,and 20 eV in four different SEP approximations and CC 1 state approximation.

The momentum-transfer cross section (MTCS) indicates the weights of backward-scattering. It is an important parameter that appears in the Boltzmann equation and describes the electron distribution function. This is useful in the study of drift velocity of a swarm of electrons moving through a particular atomic or molecular medium. Keeping this in mind,the elastic MTCSs are calculated in the energy range 0.01→20 eV. In contrast to the diverging nature of DCS in the forward direction (at the small scattering angles), MTCS shows no singularity due to the multiplicative factor (1−cosθ),

whereθis scattering angle. Figure 6 presents our calculated MTCS at four levels of SEP approximations and CC1 state approximation for CH2Br2and CCl2Br2. The shape resonances are responsible for the corresponding peaks observed in the MTCS as discussed above. The change in position of the resonance peaks is attributed to variation in polarization effects in different models. About the same trend is also seen in Fig.1 for elastic ICSs.

Fig.6. MTCS for(a)dibromomethane and(b)dichlorodibromomethane obtained in different SEP approximations and CC 1 state approximation.

4. Conclusion

In this work,we have obtained theoretical cross sections for the scattering of low-energy electrons by CH2Br2and CCl2Br2. TheR-matrix method was employed to calculate elastic differential and integral cross sections at CC 1 state level and four different SEP levels of approximations. Different virtual orbitals and different occupied valence orbitals from which single excitation are allowed,were included in the SEP calculations. Through these SEP calculations, we have performed a detailed analysis of the influence of VOs and active electrons on the elastic differential and integral cross sections.Our results in CC 1 state,SEP1,and SEP2 models show three resonances in the ICS for these two molecules. With the inclusion of more polarization effects,only two resonances remain for CH2Br2and CCl2Br2. The frist resonance seen in these models becomes a bound state. We found that polarization effects have a substantial effect on the CSs and resonances,and this effect becomes even more important for lower impact energies.

Acknowledgments

Project supported by the National Natural Science Foundation of China(Grant Nos.U1504109 and 11604085)and the Natural Science Foundation of Henan Province,China(Grant No.212300410054).