排序集抽样下定时截尾指数寿命数据的参数估计
董晓芳高阳张良勇
(河北经贸大学 数学与统计学学院,河北 石家庄 050061)
排序集抽样(RSS)方法适用于样本易于排序但不易于测量的场合,已经被应用到农林业、可靠性管理、医学等不同领域[1-6].在寿命试验中指数分布是一种非常重要的分布[7],基于RSS方法的指数分布参数的估计问题,已有一些文献进行了讨论.Bhoj[8]提出用排序集样本均值来估计指数分布参数,并证明了其估计效率高于简单随机样本均值.Zheng等[9]讨论了RSS下指数分布参数的极大似然估计(MLE),但是其似然方程没有显式解.Shadid等[10]给出了RSS下指数分布参数的修正最优线性无偏估计,数值计算结果表明RSS方法的抽样效率高于简单随机抽样(SRS)方法.Chacko[11]研究了RSS下二元指数分布参数的贝叶斯估计,证明了即使在排序不完美情形下RSS抽样效率仍然高于SRS方法.Chen等[12]考虑了RSS下单参数指数分布族参数的MLE,根据样本族的性质找到最优聚类,并在一定条件下证明了MLE的存在性和唯一性.董晓芳等[13]研究了RSS下指数分布参数的修正MLE,并给出了产品可靠度的修正估计量.
当估计指数分布参数时,文献[8-13]证明了RSS方法的抽样效率高于SRS方法.但是,这些文献研究的排序集样本测量值都是完全数据.在许多寿命试验中,由于时间、经费等限制只能得到定时截尾数据,定时截尾是指试验到指定时间就立即停止.针对定时截尾指数寿命数据的参数估计问题,本文利用RSS下定时截尾样本,研究指数分布参数的MLE及其修正估计,并比较RSS下修正MLE和SRS下MLE的估计效率.
1 排序集抽样下定时截尾样本
RSS方法的抽样步骤[14]如下:第1步,从总体中随机抽取m2个个体,随机分成m个小组,每个小组m个个体;第2步,利用主观经验判断、专家观点等易于获得的直观信息将每个小组从小到大排序; 第3步,在第i个小组内选出排序为i的个体,i=1,2,…,m.
以上3步为1次循环,进行k次循环,就可以得到样本量为n=mk的排序集样本.如果令T(i)j为第j次循环内第i个排序小组中排序为i的样本单元,那么排序集样本为T(i)j,i=1,2,…,m;j=1,2,…,k.
在定时截尾模型下,若事先规定停止试验时间为t0,则样本只能观察到

2 RSS下指数分布参数的MLE


3 RSS下指数分布参数的修正MLE


4 相对效率
令Ti(i=1,2,…,n)为抽自总体T的简单随机样本,总体T服从参数为θ的指数分布.在定时截尾模型下,若事先规定的停止试验时间为t0,则简单随机样本只能观察到


表1 估计量E 与的偏差、均方误差和相对效率Tab.1 Biases,mean square errors and relative efficiencies of estimatorsand
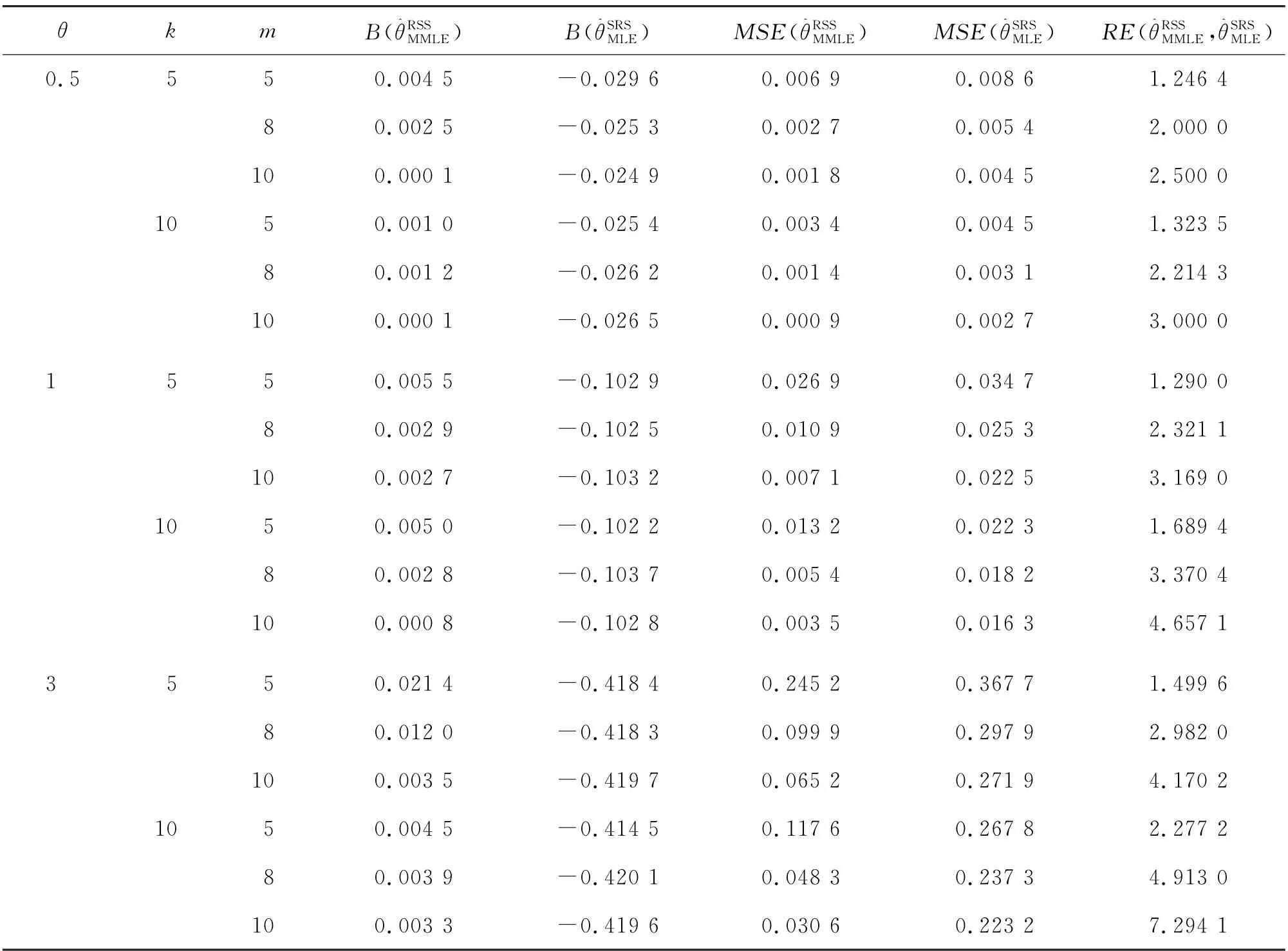
表1 估计量E 与的偏差、均方误差和相对效率Tab.1 Biases,mean square errors and relative efficiencies of estimatorsand
θ k m B(θ^RSS MMLE) B(θ^SRS MLE) MSE(θ^RSS MMLE) MSE(θ^SRS MLE) RE(θ^RSS MMLE,θ^SRS MLE)0.5 5 5 0.004 5 8 0.002 5 10 0.000 1 10 5 0.001 0-0.029 6-0.025 3-0.024 9-0.025 4 0.006 9 0.002 7 0.001 8 0.003 4 0.008 6 0.005 4 0.004 5 0.004 5 1.246 4 2.000 0 2.500 0 1.323 5 8 0.001 2-0.026 2 0.001 4 0.003 1 2.214 3 10 0.000 1-0.026 5 0.000 9 0.002 7 3.000 0 1 5 5 0.005 5-0.102 9 0.026 9 0.034 7 1.290 0 8 0.002 9 10 0.002 7 10 5 0.005 0-0.102 5-0.103 2-0.102 2 0.010 9 0.007 1 0.013 2 0.025 3 0.022 5 0.022 3 2.321 1 3.169 0 1.689 4 8 0.002 8-0.103 7 0.005 4 0.018 2 3.370 4 10 0.000 8-0.102 8 0.003 5 0.016 3 4.657 1 3 5 5 0.021 4-0.418 4 0.245 2 0.367 7 1.499 6 8 0.012 0 10 0.003 5 10 5 0.004 5-0.418 3-0.419 7-0.414 5 0.099 9 0.065 2 0.117 6 0.297 9 0.271 9 0.267 8 2.982 0 4.170 2 2.277 2 8 0.003 9-0.420 1 0.048 3 0.237 3 4.913 0 10 0.003 3-0.419 6 0.030 6 0.223 2 7.294 1
5 结论
为了提高定时截尾指数寿命数据的参数估计效率,本文利用RSS下定时截尾样本,研究了指数分布参数的MLE,并采用部分期望法对MLE进行了修正.相对效率的研究结果表明:RSS下修正MLE 的估计效率一致高于SRS下MLE.本文针对排序集抽样下定时截尾数据,未来将研究排序集抽样下定数截尾数据的参数估计问题.

