变载工况下行星齿轮裂纹沿齿根方向扩展的动力学分析
王政雯,李金展,何佳佳
(1.商丘工学院 机械工程学院,河南 商丘 476000;2.河南理工大学 机械与动力工程学院,河南 焦作 454003)
0 引 言
随着我国对环境治理的日益重视和对低碳发展的大力支持,风力发电技术得到快速发展。由于风力发电设备长期工作于丘陵、高山等环境恶劣且人烟罕至地区,受无规律变向风及强阵风冲击作用,其重要部件——齿轮传动系统长期工作于变速变载等不稳定工况下,相比于其他构件更易产生故障。同时,由于对齿轮传动系统缺乏更为科学合理的设计方法,传动过程中齿轮系统成为出现故障最多的部件[1]。此外,受随机风速循环冲击作用,齿轮副在啮合传动时易产生疲劳裂纹故障,而行星齿轮的故障率约占齿轮箱总故障率的56%。因此,对含裂纹状态下的行星齿轮传动系统进行动力学研究,对提升系统运转稳定性及可靠性,延长部件使用寿命具有重要意义。
近年来,针对风力发电行星齿轮系统故障动力学问题,国内外学者开展了大量研究工作。Mohammed等[2]根据齿轮系统的实际受力情况,对裂纹沿深度方向扩展的轨迹进行分析,研究了裂纹扩展对系统动态特性的影响。Ma等[3]对比分析认为,裂纹沿深度方向扩展比沿齿宽方向扩展对系统动态特性的影响更为明显。Liang等[4]建立了行星轮系平移-扭转耦合动力学分析模型,分析了太阳轮齿根裂纹故障对行星齿轮系统动力学特性的影响。叶舟等[5]考虑故障轮齿对系统输出响应的影响,应用动力学分析软件对正常状态及故障状态下的输出响应进行对比分析,认为故障状态下系统振动冲击现象较为严重。丁海荣[6]基于Paris研究成果,对载荷平均分布与载荷随机分布状态下的齿轮裂纹扩展轨迹及齿轮寿命进行研究。桂勇等[7]考虑误差、阻尼及时变啮合刚度等非线性因素影响,建立了行星齿轮动力学模型,得到了内齿圈、太阳轮、行星轮裂纹故障状态下的包络谱结构特性。郇立荣等[8]考虑外部激励、齿根裂纹及啮合误差等因素影响,对含裂纹的半直驱动风电行星齿轮系统固有频率及振型进行分析,并研究故障轮齿的动力学特性。董少君等[9]采用ADAMS动力学分析软件,对故障行星轮的动力学特性进行分析,得到故障轮齿的频率特征。杨之含等[10]对不同裂纹状态下的单个行星轮及多个行星轮的动态响应进行分析,认为随着故障轮齿数量的增加,系统振动程度减弱。
基于上述对行星齿轮系统故障动力学的研究成果,本文以变速、变载工况下两级风电行星齿轮系统为分析对象,假设传动过程中第一级行星齿轮系统太阳轮存在齿根裂纹故障,考虑外部负载因素,对含齿根裂纹的一级太阳轮动态特性进行分析,并对裂纹扩展状态下系统综合啮合刚度及动力学特性进行研究,以期为行星齿轮系统齿根裂纹扩展状态下的早期故障诊断提供理论依据。
1 行星齿轮系统传动原理及动力学分析
1.1 风电行星齿轮系统传动原理分析
风力发电机作为风力发电的重要装备,主要由塔架、桨叶、变桨偏航系统、电控系统、增速齿轮箱及发电机等部件组成。工作过程中,电机依靠外部风载在叶片上产生转矩带动叶片旋转并将动力由第一级行星架输入并传递至第一级太阳轮,第一级太阳轮与第二级行星架相连,由第二级太阳轮将动力输出至与发电机相连的高速级齿轮系统,高速级齿轮带动发电机转动从而实现风能→机械能→电能的转化。风电齿轮系统基本结构及传动原理如图1所示。

图1 风力发电机齿轮传动原理
图1中,s、p、c、r分别为太阳轮、行星轮、齿圈及行星架;下标1代表第一级传动,下标2代表第二级传动;下标i代表第一级传动的第i个行星轮,下标n代表第二级传动的第n个行星轮;1、2分别为高速级大齿轮1及高速级小齿轮2;Tin为输入转矩,Tout为输出转矩。
1.2 风电行星齿轮系统受力分析
传动过程中行星齿轮系统两级齿圈均固定,三个行星轮绕太阳轮均匀分布,且各轮齿物理及几何参数相同。以第一级行星传动为分析对象,采用集中质量法建立风力发电行星齿轮系统动力学分析模型如图2所示。图中OXY为行星传动固定坐标系,ks、kr、kp、kc分别为太阳轮、内齿圈、行星轮及行星架轴承支撑刚度;cs、cr、cpi、cc分别为太阳轮、内齿圈、行星轮及行星架支承阻尼;太阳轮、内齿圈、行星轮及行星架在动坐标oxy上的角位移可用θs、θr、θpi、θc表示;φi为第i个行星轮的理论位置角,φi=2π(i-1)/3,且顺时针方向为负;αs、αr为太阳轮、齿圈与行星轮间的啮合角,且αs=αr;ψsi、ψri分别为太阳轮、齿圈在坐标系上的投影角,ψsi=φi-αs,ψri=φi+αs;kspi、cspi分别为太阳轮与第i个行星轮的啮合刚度及啮合阻尼;krpi、crpi分别为齿圈与第i个行星轮的啮合刚度和啮合阻尼;espi、erpi分别为太阳轮、内齿圈与第i个行星轮间的综合传递误差。αs为太阳轮、行星轮间啮合角,αr为行星轮与行星架间啮合角。
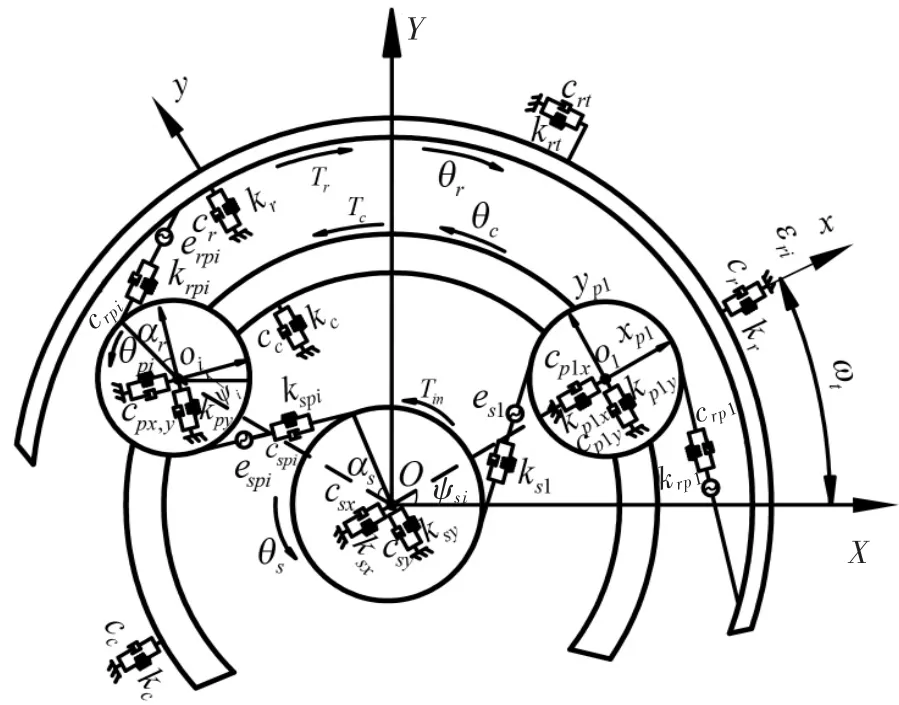
图2 风电行星齿轮传动系统动力学模型
传动过程中太阳轮、齿圈分别与行星轮啮合时产生的综合压缩变形δspi、δrpi可分别表示为:

太阳轮、齿圈分别与行星轮啮合时的动态啮合力Fspi、Frpi可分别表示为:

基于牛顿第二定律建立风电行星齿轮系统第一级传动各构件平移扭转耦合动力学分析模型,太阳轮动力学分析方程可表示为:
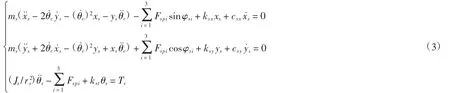
内齿圈动力学方程可表示为:
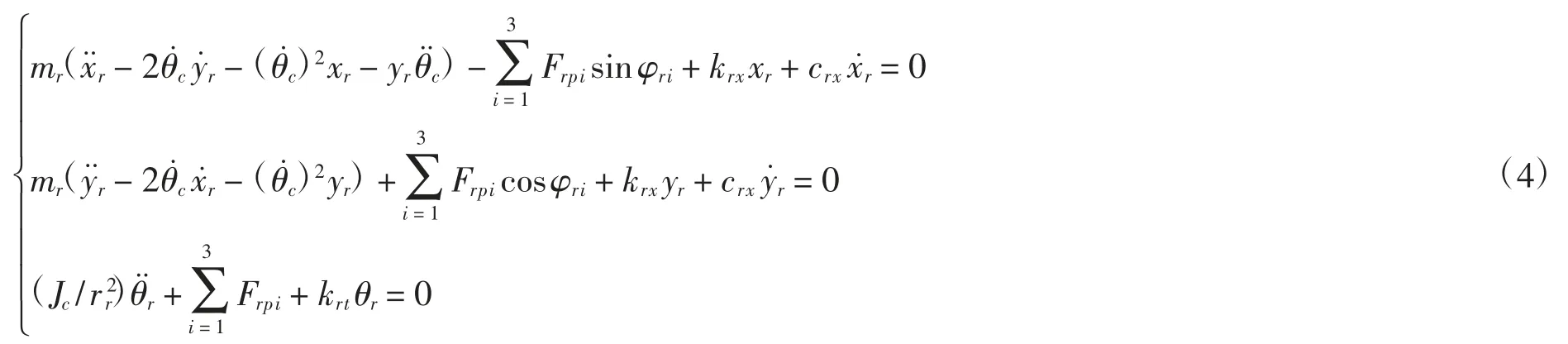
行星架动力学方程可表示为:

第i个行星轮动力学方程可表示为:

式中:ms、p、c、r代表各传动构件质量;Js、p、c为传动件转动惯量;Tc、Ts分别为第一级行星齿轮系统输入输出转矩;kux、kuy、kuθ分别为各构件x轴方向、y轴方向及θ方向支承刚度;c(s、p、c、r)x、c(s、p、c、r)y、c(s、p、c、r)θ分别为各构件在x轴方向、y轴方向及θ方向支承阻尼;δpix、δpiy、δpit分别为行星架相对于行星轮在坐标系上产生的弹性变形。
综上所述,将风电行星齿轮系统动力学微分方程写成矩阵形式,可表示为:

式中:M为质量矩阵;G为陀螺矩阵;Cb、Cm分别为支撑阻尼矩阵及啮合阻尼矩阵;Kb、Kg分别为支撑刚度矩阵及啮合刚度矩阵;Kw为向心刚度矩阵;F、T分别为内外部激励矢量。
1.3 外部风载分析
由于外部风载受地势、季节等因素影响,使得齿轮系统所受外部载荷具有较大程度的随机性。本文以平均风速为13.4 m/s的随机风作为传动系统所受负载,采用自回归模型线性滤波法对齿轮系统所受随机风载进行模拟,结果如图3所示。

图3 随机风速模拟
2 齿根裂纹扩展对啮合刚度影响
假设第一级太阳轮存在齿根裂纹现象,随着构件的运转,裂纹沿齿根方向不断向轮齿中线方向扩展,如图4(a)所示。传动过程中故障太阳轮每转动一周将与行星轮产生三次啮合冲击。太阳轮输入转矩为4.484×106N·m,构件运转初始状态下无裂纹产生,随着构件的运转,裂纹深度由0逐渐增加为q,裂纹与齿轮中线的夹角为ν,gc为裂纹末端点在齿廓上的投影P与齿根间的距离,裂纹扩展参数模型如图4(b)所示。传动过程中当裂纹扩展至齿厚的一半时,轮齿将发生折断事故,故本文只考虑裂纹深度小于齿厚一半的情况。

图4 裂纹扩展分析模型
当轮齿齿根产生裂纹时,计算轮齿所需的转动惯量及截面面积均发生变化。截面面积的改变对轮齿弯曲刚度、剪切刚度产生较大影响,并进一步影响轮齿综合啮合刚度。齿根裂纹的产生并不影响轴向压缩刚度及赫兹接触刚度,故传动过程中仅考虑截面面积的改变对综合啮合刚度的影响。含裂纹轮齿综合啮合刚度可表示为

式中,kbs、kas、kcs为裂纹轮齿弯曲刚度、压缩刚度及剪切刚度,kbp、kap、kcp为行星轮弯曲刚度、压缩刚度及剪切刚度,kh为赫兹接触刚度。
传动过程中含齿根裂纹的太阳轮随系统的运转裂纹不断扩展,定义太阳轮裂纹深度q与齿厚的比值为裂纹占比,裂纹扩展角ν=45°。含裂纹的一级行星齿轮系统基本参数如表1所示。

表1 一级行星齿轮系统基本参数
根据表1的基本参数及含裂纹的综合啮合刚度计算式(8),对无裂纹及不同裂纹占比状态下齿轮啮合刚度进行仿真分析,结果如图5所示。
由图5可知,随着裂纹的不断扩展,轮齿啮合时综合啮合刚度逐渐减小。同时,在第一个双齿啮合区,齿轮发生裂纹时的综合啮合刚度略小于无裂纹状态下轮齿的综合啮合刚度。当轮齿由双齿啮合区过渡到单齿啮合区时,故障轮齿的综合啮合刚度明显小于正常状态下轮齿的综合啮合刚度,且当出现第二个双齿啮合区时,故障轮齿与正常轮齿间啮合刚度的差值明显大于第一个双齿啮合区。产生此现象的原因在于裂纹轮齿与正常轮齿逐渐啮合,轮齿所受负载逐渐增大,裂纹对轮齿啮合刚度的影响逐渐增加。在单齿啮合阶段,故障轮齿承担所有负载,其综合啮合刚度在整个单齿啮合区明显比正常状态下轮齿的啮合刚度小。当齿轮裂纹占比大于40%时,单齿啮合状态下齿轮的啮合刚度下降趋势更为明显,表明裂纹的存在已对轮齿的啮合刚度产生较大影响,应及时更换裂纹轮齿以避免断齿故障的产生。
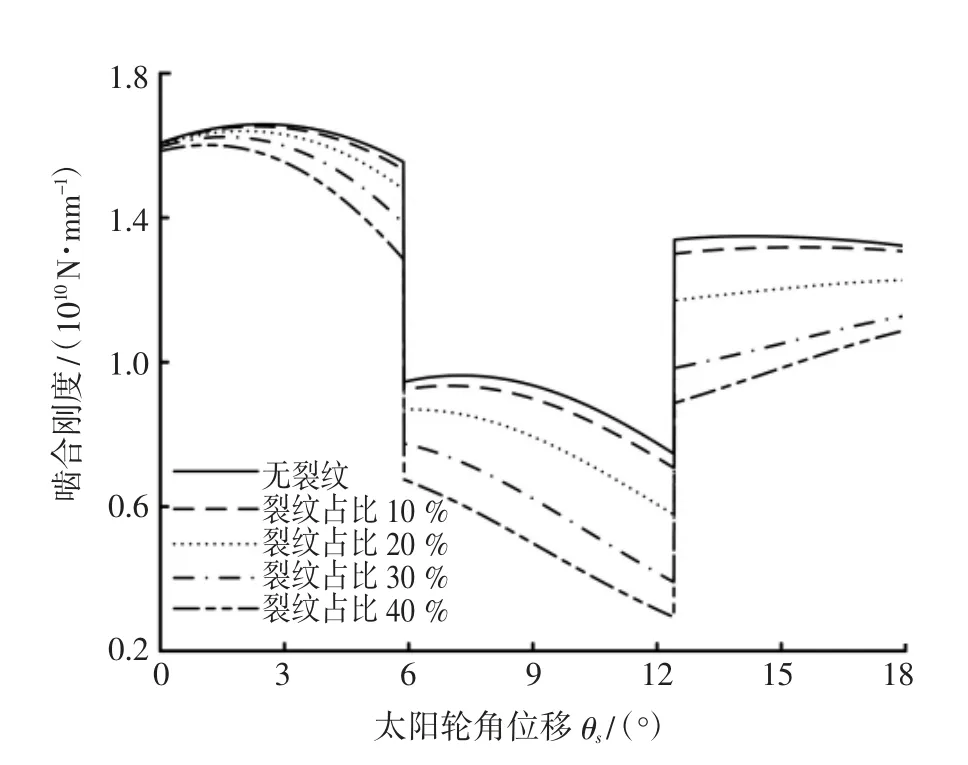
图5 裂纹占比不同时的轮齿啮合刚度
3 裂纹扩展对行星齿轮系统动力学特性影响
对于故障轮齿而言,传动过程中系统所受动态激励不仅受刚度激励影响,还受轮齿啮入啮出时的啮合冲击激励影响。为便于求解系统的动态特性,对第一级行星齿轮系统输入转频fc及啮合频率fm进行计算:

式中:nc为行星轮转速,nH为行星架转速,zc为行星轮齿数,i(i=1,2,3……)为频率谐波。
基于第二节建立的风电行星齿轮系统动力学模型,考虑外部风载及齿根裂纹等因素影响下齿轮啮合刚度的变化情况,将所求解的综合啮合刚度带入式(7),并对无裂纹扩展、齿根裂纹扩展10%、20%、30%及40%状态下的x向振动加速度进行时域及频域分析,结果如图6所示。
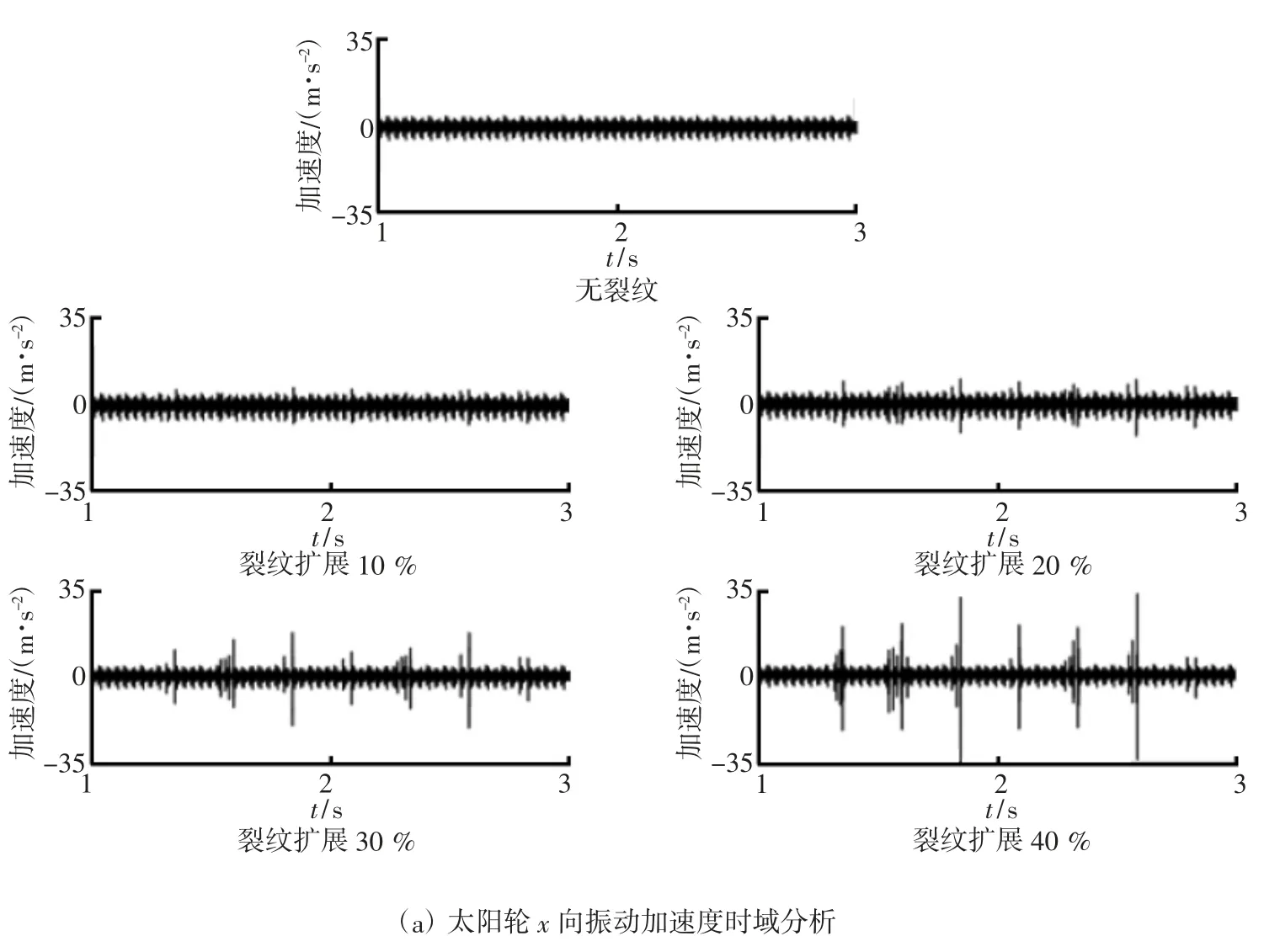
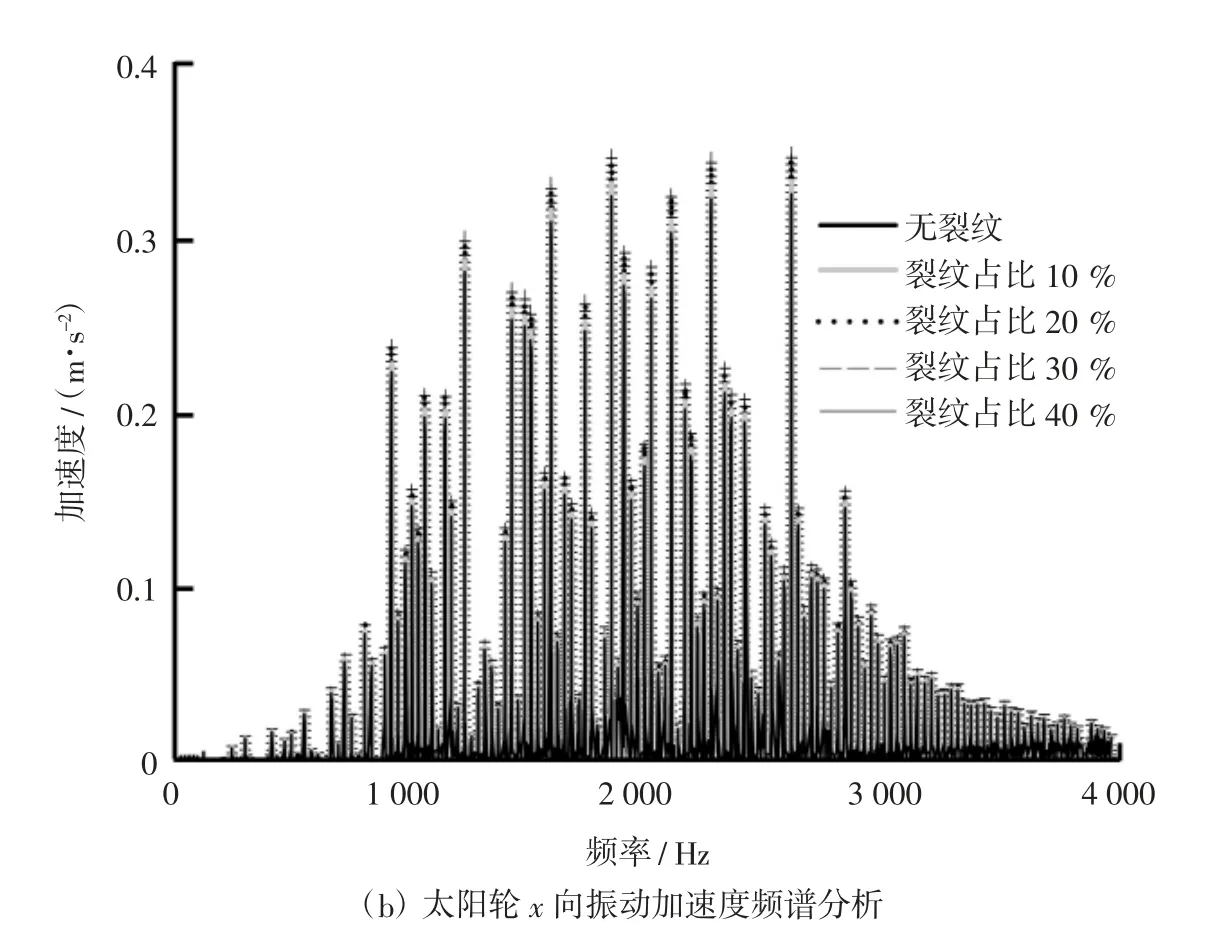
图6 裂纹轮齿x向动态特性时频分析
由图6可知,当太阳轮齿根裂纹沿齿根向中心线方向扩展时,太阳轮x向动力学特性呈现一定的周期性变化,且随着裂纹扩展比例的增加,系统所受动态冲击增大。传动过程中,当系统由无裂纹状态扩展至裂纹占比10%时,系统所受局部冲击现象并不明显。当裂纹扩展至20%时,系统所受动态冲击增加,且裂纹扩展占比越大系统所受局部冲击越严重。产生这种现象的主要原因是,随着裂纹扩展比例的增加,太阳轮、行星轮啮合过程中由双齿啮合过渡到单齿啮合状态时,系统综合啮合刚度减小程度急剧增加,从而导致传动过程中系统所受动态特性发生突变。
图7为裂纹轮齿x向振动加速度局部细化频谱。由图7可知,随着裂纹的扩展其频率响应峰值均出现在系统啮合的倍频处,且在最大频率处易产生较严重的边频带现象。图7还显示,在有、无裂纹状态下太阳轮的边频成分均基本相同,相邻两边频成分间的差值即为太阳轮的故障频率。同时,随着裂纹扩展程度不断增加,相邻边频带间的峰值不断增大,故障轮齿所对应的振动冲击响应及频率响应调制现象越严重。
4 结 论
本文以两级风电行星齿轮系统为分析对象,针对一级太阳轮存在的齿根裂纹现象,通过对不同程度的齿轮裂纹扩展模型进行动力学分析求解,得到结论如下:
(1)对不同裂纹扩展状态下太阳轮、行星轮综合啮合刚度进行分析可知,随着裂纹扩展程度的增加,太阳轮-行星轮综合啮合刚度逐渐下降,且在双齿啮合区过渡至单齿啮合区时,综合啮合刚度变化最为明显。此外,当齿轮裂纹占比大于40%时,单齿啮合状态下齿轮的啮合刚度下降明显。因此,为避免轮齿折断事故的发生,应尽可能更换故障轮齿以达到较好的传动效果。
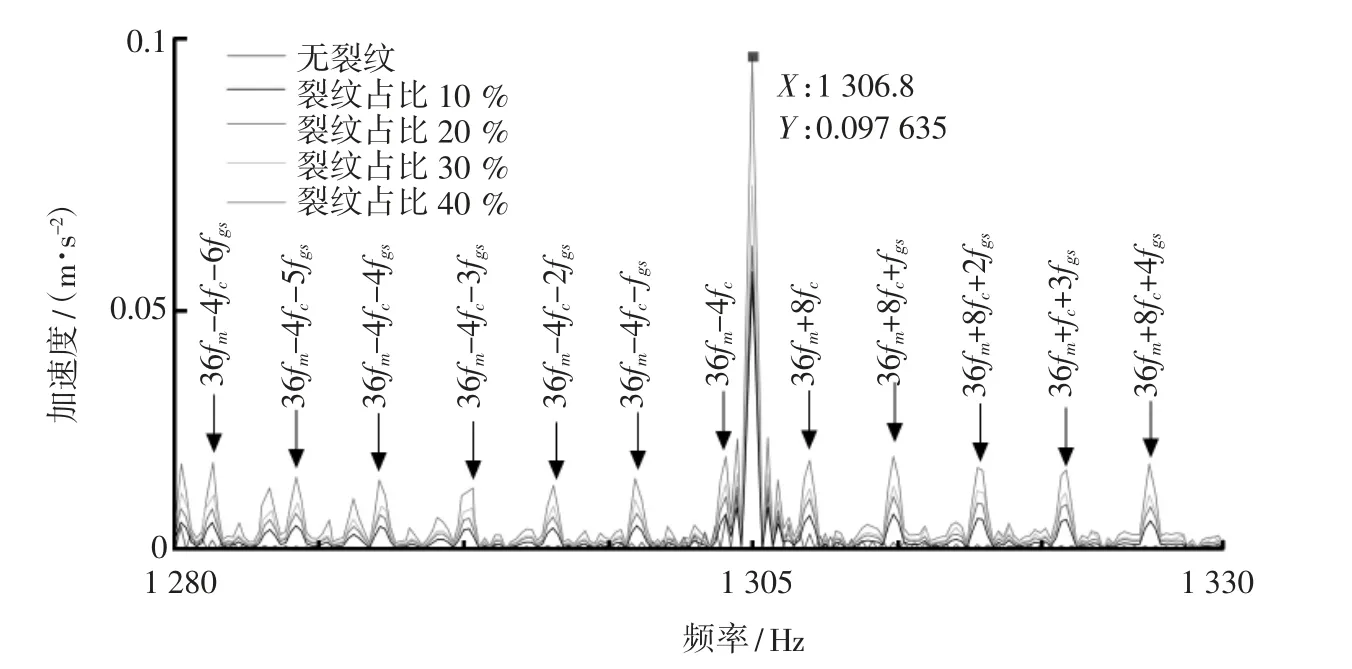
图7 裂纹轮齿x向振动加速度局部细化频谱
(2)基于裂纹状态下动态啮合刚度分析,对行星齿轮系统裂纹占比不同状态下太阳轮在x向振动加速度进行求解。结果表明,随着裂纹占比增加,轮齿所受振动冲击明显增大,当裂纹占比由30%增至40%时,振动加速度产生突变,系统所受振动冲击更为明显。
(3)对太阳轮故障占比不同状态下太阳轮x向振动加速度频谱进行分析,结果表明,随着裂纹扩展程度增加,相邻边频带间的峰值差增大,且当裂纹占比由30%增至40%时,故障边频带产生突变,导致轮齿折断事故。研究所得结果可为早期轮齿故障诊断提供理论依据。

