企业原材料订购与运输决策问题探究

徐浩钧，陈 昂，周福盛

（江苏大学 a.数学科学学院；b.汽车与交通工程学院，江苏 镇江 212013）

某建筑和装饰板材的生产企业所用原材料主要是木质纤维和其他植物素纤维，总体分为A、B、C三种类型。该企业每年按48周安排生产，需要提前制定24周的原材料订购和转运计划，即根据产能要求确定原材料供应商和每周需要订购的相应原材料数量，确定第三方物流公司并委托其将供应商每周的原材料供货转运至企业仓库。2021年全国大学生数学建模大赛C题[1]附件给出该企业近5年402家原材料供应商的订货量和供应数据，8家转运商的运输损耗率数据，要求对生产企业原材料的订购与运输决策问题进行探究。本文拟基于熵权法针对赛题要求逐一建模求解，对供应商进行综合评价[2]，以确定对企业最重要的供应商，并给出优化订购运输方案。

1 问题一模型的建立与求解

1.1 供应商供货特征指标选取及标准化处理

（1）供货比

供应商i的供货比是指在240周内，企业向供应商i订货的次数占总周数的比例，表示为

其中，ni为企业在240周内向供应商i订购原材料的次数。经标准化处理后的供货比为

（2）平均供货量

平均供货量βi是指供应商每次提供的平均货量，表示为

其中，pij为供应商i第j周的供货量，mi为剔除异常数据后供应商i的总供货次数。

为消除数量级差异影响，得到较为合理的数据，将平均供货量取对数后再进行极差变换。

同样对平均供货量βi进行标准化处理，得到

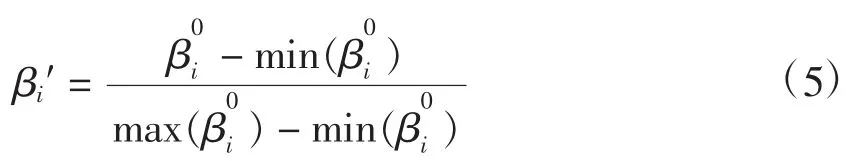
（3）平均订货量

平均订货量φi是指企业每次向供应商i订购的平均货量，表示为

其中，qij为企业第j周向供应商i的订货量，ni为剔除异常数据后企业向供应商i的总订货次数。

分析数据可发现，平均订货量在数量级上的差异和平均供货量类似，因此，对该数据同样先取对数，再进行标准化处理。

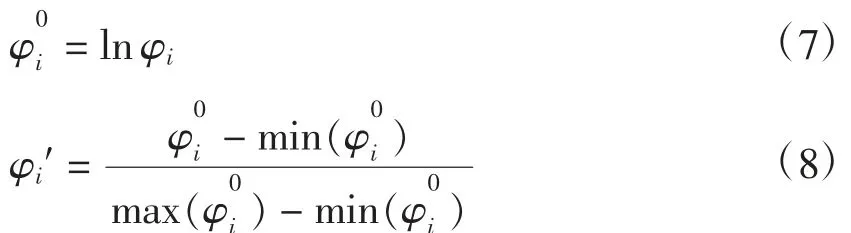
（4）供订比

现实生产中存在企业向供应商订货但供应商拒绝发货的情况，所以引入供订比判定各供应商的供应信誉。供订比越大，信用程度就越高，特征值越大。供订比σi表示为

其中，mi为供应商i的供货次数，ni为企业订货次数。同样对σi进行标准化处理，得到

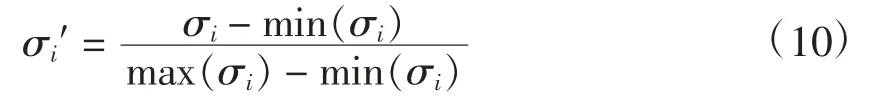
（5）订货量变异系数

变异系数是衡量各观测值变异程度的统计量[3]。某一供应商订货量的变异系数直接反映了该供应商供货的稳定程度，其值同时受平均数和标准差两个统计量的影响。将企业240周内向供应商i的周平均订货量记为μi，周订货量的标准差为σi，则供应商i的订货量变异系数Ci可表示为

将订货量变异系数Ci标准化处理。由于Ci为极小型变量，首先采用倒数变换将其一致化处理，得到极大型变量Ci′，

则标准化后的订货量变异系数Ci″为

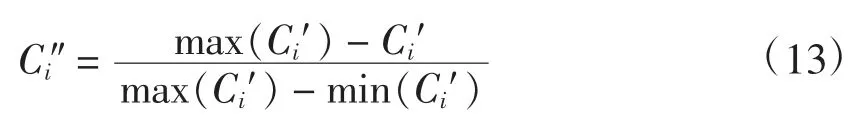
对上述5个评价指标分析计算，得到各供应商量化的供货特征指标如表1所示（部分），各特征指标用xik表示（i=1，2，…，402，k=1，2，…，5）。

表1 各供应商供货特征指标（部分）

1.2 供应商对企业重要性的量化分析

（1）熵权法计算权重

熵权法是一个相对客观的赋权方法，可很大程度地避免主观影响[2]。上文已对5个指标进行了正向标准化处理，为方便描述，用zk，i表示第i个供应商的第k个指标的标准化数值，计算第k个特征指标的信息熵ek，

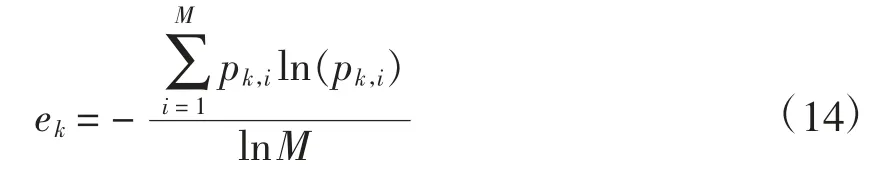
其中，pk，i是第i供应商的第k个特征量在第k特征量总和中所占的比例，即

信息熵越大，特征指标的信息越少，因此需要对其进行正向化处理，而计算其对应的信息效用值dk可正向衡量信息量，

最后，再进行归一化处理，得到各供应商特征指标的熵权wk（k=1，2，3，4，5）

经计算得到5个特征指标权重如图1所示。

由图1可见，平均供货量所占权重最大，其次是平均订货量，供货比次之，而供订比和变异系数所占比重相较于前三者非常小，供订比权重甚至小于10－10，说明供订比不能反映供应商的供货特征。最终，得到评价重要性的4项指标如表2所示。

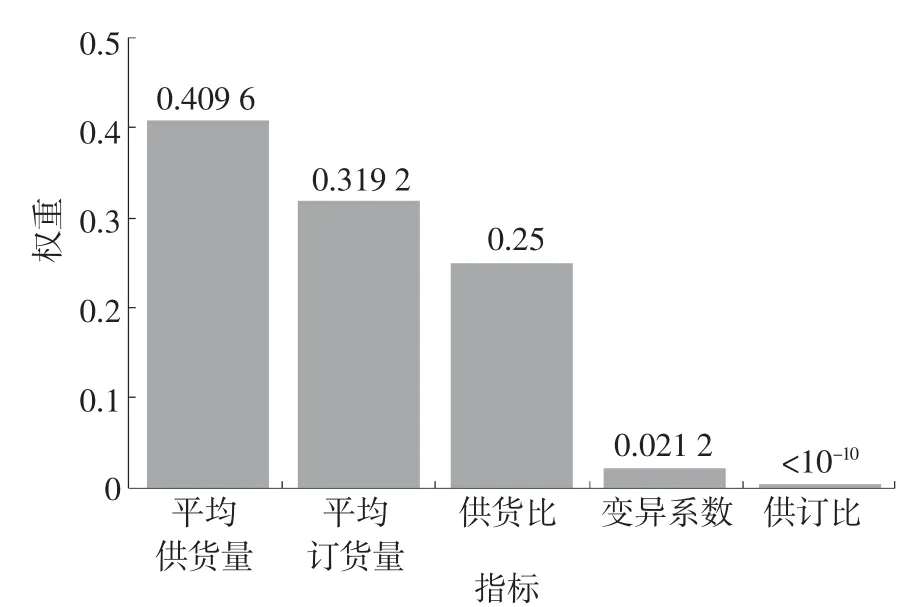
图1 各供货特征指标权重

表2 评价供应商供货特征重要性的4项指标

（2）综合评价模型的建立

为简化问题，假设各项供货指标间相互独立，选择线性加权函数作为综合评价模型，综合评价402家供应商对企业的重要性[4－5]。令Yi为供应商i的重要性综合得分，则

其中，wk为第k个供货指标的权重，xik为供应商i第k个供货指标。

经计算得到402家供应商量化的重要性综合得分，确定50家对企业最重要的供应商，并用南丁格尔图呈现综合评价模型，结果如图2所示。

2 问题二模型的建立与求解

2.1 满足生产需求的供应商最小数量选择

引入0－1变量yij，若企业第j周向供应商i订货，则yij=1，反之则yij=0。

各供应商供应的原材料种类不同，企业生产单位产品所需各类原材料的数量也存在差异，因此用ki表示生产单位产品所需供应商i的原材料数量。企业生产每m3产品需消耗A类原材料0.6 m3，B类原材料0.66 m3，C类原材料0.72 m3，而各供应商生产原材料的种类固定，即ki为固定值，ki∈{0.6，0.66，0.72}。

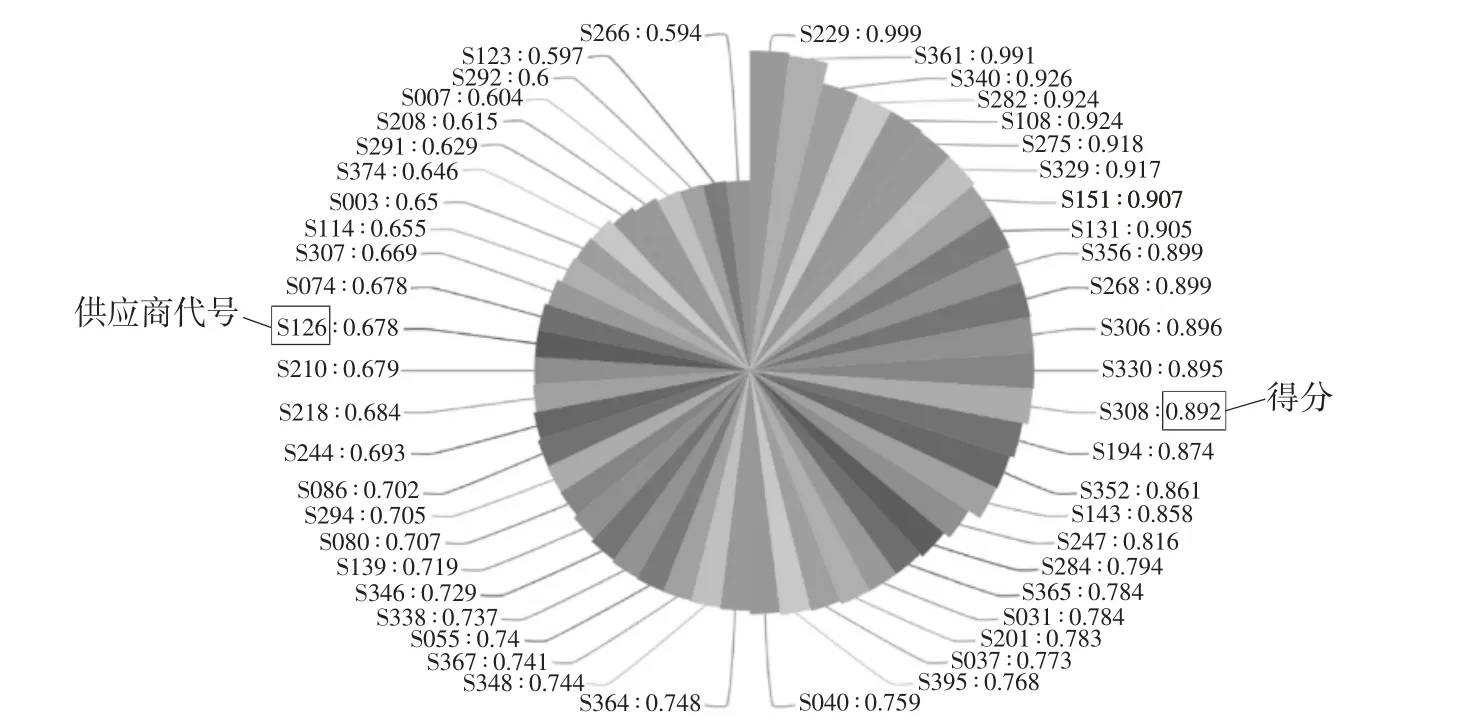
图2 50家最重要的供应商及其综合得分

用xij表示企业第j周向供应商i的订货量，则企业在第j周订购原材料的总量sj可表示为

企业第j周总订货量可带来的预计产能qj可表示为

由上述分析建立目标规划模型。

（1）目标函数确定

决策目标设定为企业24周内供应商的选择数量，决策变量为0-1变量yij，则目标函数可表示为

（2）约束条件确定

1）企业每周的产能至少为2.82×104m3，即

2）因不同供应商的供应能力不同，引入参数Hij表示供应限制。Hij可用过去5年中每个上半年（24周）各供应商在各周以及前后两周内的最大供货量表示（每年的第一周数据用每年前两周的数据确定）。用tij（k）表示过去第k年供应商i的供货量，则供货限制Hij可表示为

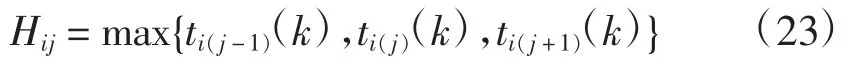
3）企业在向供应商订购原材料时，需要考虑订购量不能超过供应商的最大供货能力，即

（3）模型建立与求解

建立满足生产需求的供应商选择数最小的数学模型为

使用Lingo模型求解，可得最优解z1=265。同时，根据对最优解的分析，得到企业在未来24周每周选择供应商的最小数目mj，结果如图3所示。

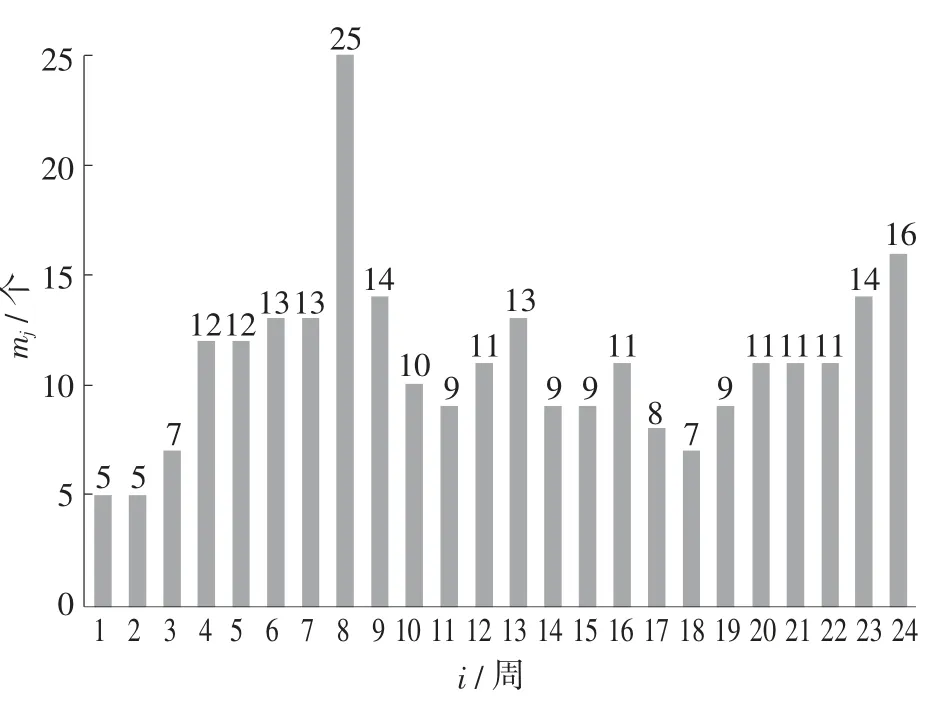
图3 每周最少需选择的供应商个数

2.2 最经济订购方案模型

由图3知，未来24周企业向402家供应商订货时，每周至少选择供应商的数量mj最多可达25家。为避免一些综合评分很低的企业也可能被选中订货，对上述模型进行优化。

将模型候选供应商的参考范围从全部402家压缩为问题一所求的最重要的50家，足以满足生产需求。

由题意，此规划问题的优化目标是：在供应商确定的前提下，获得订货费用最小的原材料订购方案。设C类单价为1，A类为1.2，B类为1.1，即每家供应商原材料的单价di固定，di∈{1，1.1，1.2}。设企业第j周的原材料订购总费用为ej，24周总费用为E，则目标函数可表示为

达到最优目标的同时，需满足以下约束条件：

（1）企业每周的订货量依旧受各供应商供货能力所限，即

（2）每周选择供应商的数量应为mj，即

（3）企业在第j周预计产能qj要大于企业每周的产能，即

综上，建立该企业未来24周每周最经济的原材料订购方案模型为

使用Lingo求解得模型的最优解E=488 047，同时，可得企业在未来24周最经济的原材料订购方案（部分）如表3所示，其中，D表示供货，O表示订货。

2.3 模型结果的实施效果分析

由于供应商不一定能保证严格按订货量供货，利用SPSS统计，给出各供应商的供订比频率分布直方图和供订比的正态P-P图。如图4、图5所示，各供应商供订比频率近似服从正态分布。

表3 未来24周最经济的原材料订购方案（部分）

图4 各供应商供订比频率分布直方图

图5 供订比的正态P-P图

运用MATLAB构造正态分布随机矩阵T[6]，模拟未来24周内各供应商的实际供订比，得到未来24周50家供应商的实际供货矩阵v，

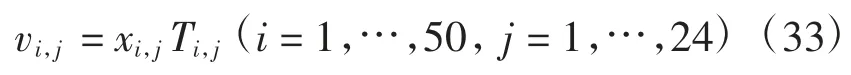
根据原材料类别，对供应商进行分类，按照企业生产单位产品所需不同原材料的供货量，模拟未来24周的企业产能，作折线图，评估方案实施效果。如图6所示，在问题二的订购方案下，企业产能相对稳定，实施效果良好。

图6 问题二订购方案的模拟产能与原有计划产能

在订购方案模型中用损耗率均值代替损耗率，给出相应的订购方案，但实际情况下损耗率均值不可能完全真实表示损耗率。可通过引进0－1变量R表示符合实际情况的损耗率，

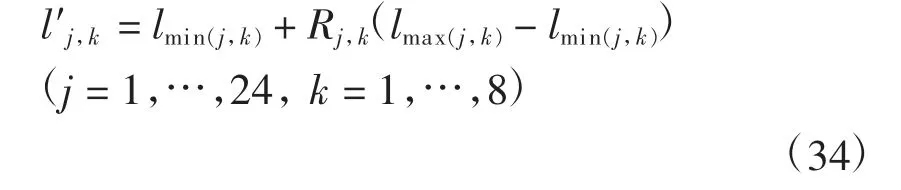
再按随机损耗率和损耗率均值作折线如图7所示，评估方案实施效果，结果达到预期。

图7 问题二转运方案情况下损耗率情况

3 问题三模型的建立与求解

问题三的模型与问题2类似，其关键是如何让模型遵循“尽量多采购A类和尽量少采购C类”的规则，为此需引入一些新变量和新限制条件。

首先，引入变量xsup（j，k），表示第j周第k类的订购上限（为方便表述和编程，令A为1、B为2、C为3），其值与规模限制H相关，具体表示为

同时，构造各周对各类原材料的计划订购总量x0，具体表示如下：

最后，为了表示订购量达到订购上限，构造0－1变量xif（j，k），

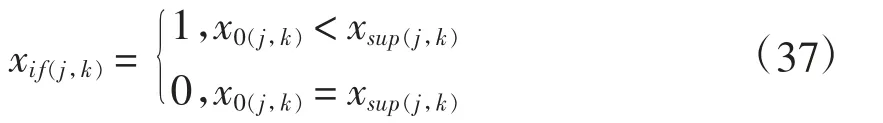
接下来，讨论新的限制条件，即“A类的订购量达到上限时才会订购B类，当B类订购达到上限时才会订购C类”。不订购B类，不订购C类分别用等式x0（j，2）=0，x0（j，3）=0表示。

限制条件表示为

建立企业未来24周最经济原材料订购模型

使用Lingo求解得模型最优解E=516 062，以及企业未来24周每周最经济的原材料订购方案。

4 问题四的建模与求解

根据实际情况，企业产能受供应商的供货情况与转运商转运能力影响。如图8所示，50家综合评价高的供应商的供货上限之和与全部402家供应商供货上限之和相差无几，故可用综合指标前50家供应商的供应能力代表供应商供应能力。

图8 得分前50的供应商供应量占比

另外，为确定企业产能增加的上限，在制订订货方案时，不考虑节约仓储成本。建立优化模型，以确定改进后部分企业的产能上限。

若企业每周产能用Qj表示，则目标函数为

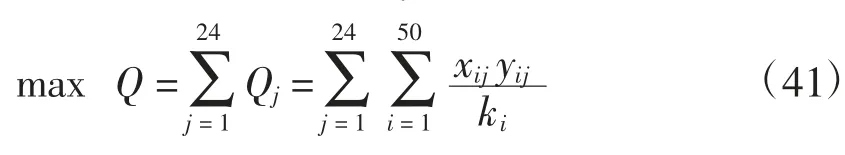
供货上限与转运能力限制表示为

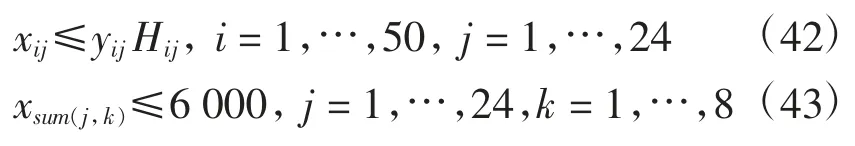
企业每周产能上限的最优化模型为

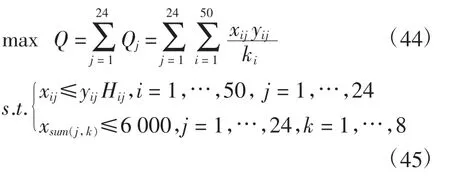
利用Lingo求解，得到企业未来24周每周最大产能，以及在该产能下企业向50家供应商订购原材料的方案和转运商的选择方案，并得到在产能提高后企业每周产能变化情况。

5 结束语

本文探究了企业原材料的订购与运输决策问题，根据所给数据，计算得到各生产商、转运商的综合评分，并针对不同情况建立不同模型，得到相对合理、经济的原材料订购和转运方案，完成了2021年全国大学生数学建模大赛C题任务，效果达到预期。