基于射频数据的道路交通流路径识别优化模型

任其亮，徐韬，程龙春

（1.重庆交通大学，重庆 400074；2.重庆市市政设计研究院有限公司，重庆 400020）

0 引言

相较于单一车辆路径识别，道路断面交通流路径识别更能反映道路流量走向、车流构成等出行特征，因而广泛应用于道路前期论证、交通组织优化等工程应用，目前道路交通流路径识别主要通过人工车牌计数、高清卡口、车载射频识别车牌数据等大数据挖掘实现。

吴俊美[1]依托RFID （Radio Frequency Identification）数据提出城市道路交通流特征参数提取与预测模型，实现车辆路径识别及城市道路交通流特征参数预测。杨冰健[2]根据卡口数据基于TOPSIS （Technique for Order Preference by Similarity to Ideal Solution）法从多义卡口对合理路径集中识别最合理路径，实现机动车多义轨迹段路径识别。刘迎等[3]基于RFID 及GPS 数据采用ARIMA（Autoregressive Integrated Moving Average Model）、改进的SVM（Support Vector Machine）模型对公交车行程时间进行预测，验证了RFID 数据的有效性。李军等[4]利用历史出行轨迹计算得到路段间的转移概率，并建立Markov 链模型识别出行者路径轨迹。潘义勇等[5]建立随机交通网络环境下约束最可靠路径模型，研究模拟仿真交通环境下风险性车辆的路径识别。吴金锁[6]利用FP-growth（Frequent Pattern growth）算法基于RFID 数据提出基于时间阈值的车辆轨迹分割算法，进而得到车辆出行次数与停留位置等交通参数，肖清榆[7]根据高速公路联网收费数据利用改进蚁群算法求解高速路网中多合理路径问题。

综上，为保障单一数据源下路径识别精度，目前交通流路径识别对数据覆盖质量要求较高，主要以高速公路等样本数据覆盖密集的路段为主，对城市次支道路等RFID、卡口覆盖不足路段考虑相对较少。在实际工程应用中，RFID 点位主要集中在快速路、主干路等骨架道路，次干路、支路覆盖较少，导致传统分析结果误差较大。基于此，本文依托RFID、FCD等交通大数据，通过组合算法模型构建城市道路断面交通流路径识别体系，提升了路径识别估算精度。

1 断面交通流路径识别体系

1.1 交通流与车辆路径

通过车辆行驶路径叠加获取本文断面交通流，车辆行驶路径则通过组合模型进行识别或估算，假设所有车辆由节点1行驶至节点14，则统计时段内任意路段l（i,j）交通流q（i,j）为途经节点i、j的车辆集合数，如图1所示。

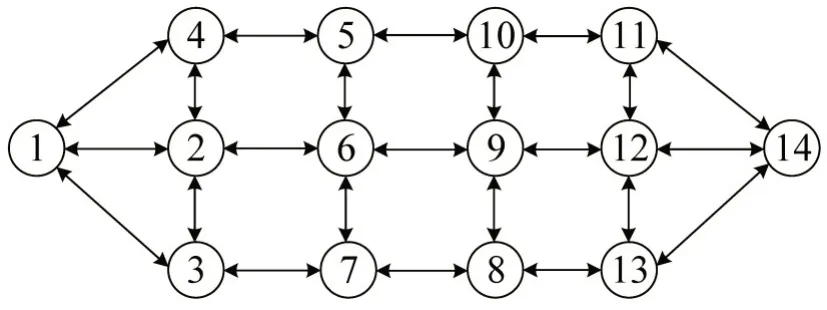
图1 城市GIS路网示意图Fig.1 Schematic diagram of urban road GIS network

1.2 路径识别过程

假设追溯目标断面为l（6,9），在交通组织、交通规划等工程应用中，相交于识别单个车辆行驶路径，更倾向于获取道路追溯断面各进出口连接道路交通流分布情况，识别各连接道路途径追溯断面的交通流，而非单个车辆路径追溯，即转化为求解l（6,9）交通量中途经l（2,6）、l（9,12）等l（i,j）路段的追溯交通流问题。

通过RFID 接收器统计途径车辆编码ID 并计算出l（6,9）断面交通流q，利用平移不变小波变换[8]（Transition Invariant Discrete Wavelet Transform，TIDWT）将q切分为平稳项和随机项q′。按车辆途径RFID监测点数量将分为可追溯交通流（该车辆通过或驶出目标断面RFID监测点及途径次数不小于3 次）和非追溯交通流（该车辆通过RFID监测点次数不大于2次），即

计算步骤如下。

Step 1 根据FCD-RFID追溯路径模型，求解出l（i,j）可追溯交通流。

Step 2 依托城市出行OD 矩阵，利用基于综合成本阻抗的路径感知随机用户均衡模型（Route Perception Logit-Overlapping Stochastic User Equilibrium, RPL-O-SUE）以l（6,9）为追溯目标断面进行交通追溯分配，结合GIS 路网中RFID 点位分布情况，将除追溯目标断面RFID 点外途径其余RFID点位次数超过2次及以上次数的车辆剔除，即统计出由交通分配模型初定l（i,j）的非追溯交通流，并扩样出最终非追溯交通流为

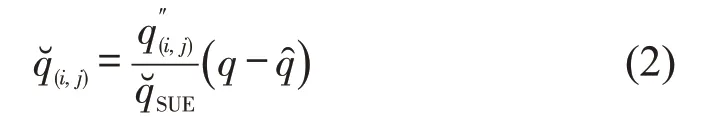
式中：为初定的路段l（i,j）非追溯交通流；为追溯目标断面SUE模型预测交通流；为路段l（i,j）最终非追溯交通流。

Step 3 考虑外地车辆比例α，重庆市中心城区外地车比例为6.3%～7.5%之间，本文取α=7%，计算出为

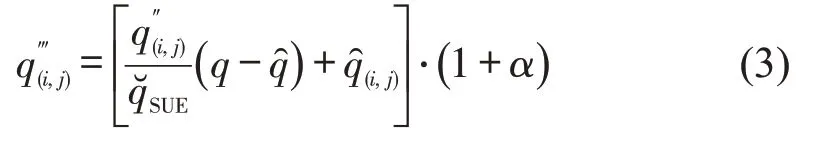
2 模型建模

2.1 TIDWT切分RFID

按周期时长1 min 统计建立追溯目标断面RFID 交通流时间序列，利用TIDWT 将RFID 交通流数据切分为平稳项和随机项，TIDWT 未筛选出具体车辆ID 信息，故需先将随机项数值匹配至RFID车辆ID进而筛选出噪声车辆ID，步骤如下。

Step 1 利用TIDWT切分出平稳项和随机项并向下取整。

Step 2 计算统计周期内每辆车与前一辆车通过RFID监测点时间间隔与平均时间间隔差值绝对值，按降序排列，根据Step 1 计算的该统计周期内噪声车辆总数，由大到小筛选出该周期内同数量的噪声车辆ID。

Step 3 重复Step 2 筛选出每个统计周期内噪声车辆ID并剔除，即得到平稳项数据。

2.2 FCD-RFID追溯路径模型

利用FCD（本文为出租车GPS 数据）计算路段实时动态行程车速，进而标定路段s估计行程时间（点j到点j+1 中路段s估算行程时间），通过累计求和得到该路径估计行程时间，将所有路径行程时间和RFID监测起讫点实际行程时间绝对误差最小路径作为估计路径，以间隔时间绝对误差最小为目标建立目标函数为

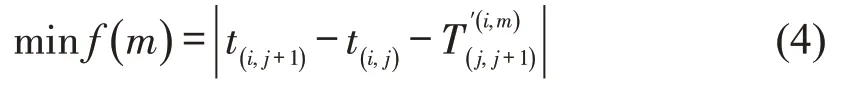
式中：为车辆i在点j到点j+1 间第m条路径估算行程时间。

根据浮动车在统计时间路段中数量qs将路段分解为Full 型（qs≥3）、Defect 型（1≤qs≤2）、Null 型（qs=0）这3类。

（1）Full

该类型路段估计行程时间t′s数值等于通过FCD计算出的行程时间，即

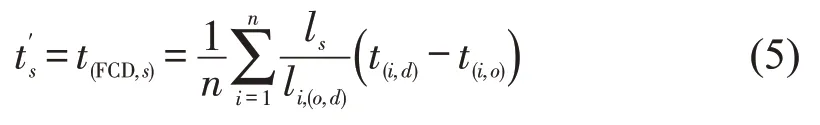
式中：t′s为路段s估计行程时间；t（FCD,s）为基于FCD计算行程时间；ls为路段s里程；li,（o,d）为第i辆浮动车行驶里程（出租车每15 s返回一次数据信息）；t（i,d）为第i辆浮动车在该路段终点时间；t（i,o）为起点时间；n为统计时间内浮动车数量。

当该路段里程小于浮动车在15 s 内行驶里程时，则将起点和终点顺延至前路段和后路段，并参照式（5）计算路段实际行程时间。

（2）Defect型

为t（FCD,s）及通过历史FCD 计算的行程车速加权求和值，令，α、β为待定权重系数。

（3）Null型

为及该统计时段内道路等级自由流车速下行程时间加权求和值，令为该时段内该类型等级道路自由流车速（道路等级分为快速路、主干路、次干路、支路这4 类），α1、β1为待定权重系数。

2.3 基于综合成本阻抗的RPL-O-SUE模型

通过基于综合成本阻抗的RPL-O-SUE交通分配模型求解断面交通流中的非追溯交通流及随机项，传统效用函数多以出行时间成本进行标定，但未考虑道路品质和驾驶惯性。本文综合考虑出行时间、道路等级和驾驶偏好因素，将出行者决策类型分为成本决策、认知决策和惯性决策这3 类，通过相继平均法求解[9]，并采用均方根误差（Root Mean Square Error,RMSE）作为收敛准则进行收敛性判断，则路径k效用函数F（rs,k）为

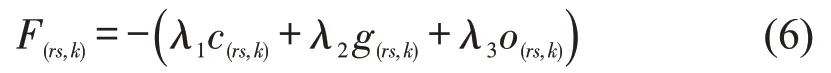
式中：F（rs,k）为路径k的效用函数；c（rs,k）为路径k出行时间成本特征值；g（rs,k）为路径k认知决策特征值；o（rs,k）为路径k惯性决策特征值；λ1、λ2、λ3均为待定参数，且λ1+λ2+λ3=1。

c（rs,k）为出行时间成本函数，本文不再赘述，g（rs,k）由路径道路等级确定，判断模型为

对于该路径包含多个路段且涉及多类道路等级时，根据路段里程占该路径总里程比例进行求和运算，为路径k总里程，n为路径k所含路段总数量。

o（rs,k）由历史出行次数确定，判断模型为

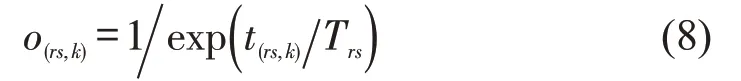
式中：t（rs,k）为统计时段内起点r和终点s中选择路径k的出行次数；Trs为统计时段内起点r和终点s中出行总次数。

效用函数F（rs,k）反映了出行时间、道路等级和驾驶偏好对路径选择的影响程度，因此可通过计算上述因素重要性标定λ1、λ2、λ3。本文设计了Likert五分量表问卷调查表，组织223位驾驶员志愿者参与问卷调查，其中男性128 位，占57.4%，女性95位，占42.6%。结果显示，出行时间、道路等级和驾驶偏好得分均值分别为4.5、2.0、1.3，重要性分别为0.56、0.26、0.16，由于驾驶偏好得分均值至少为1.0，相应其重要性至少为0.09，故可知驾驶偏好对驾驶员路径影响较小。为减少算法复杂度，本文在不考虑驾驶偏好影响下，出行时间、道路等级重要性分别为0.69、0.31，故本文λ1=0.69、λ2=0.31、λ3=0，同时在不考虑算法复杂度下，也可取λ1=0.58、λ2=0.26、λ3=0.16。

3 案例分析

3.1 数据基础

依托重庆市中心城区道路运行监测系统，目前已接入RFID 监测点1154 处，其中内环以内846 处（73%），内环以外308处（27%），同时选取5条道路为校核路段，其中快速路2条，主干路3条。

3.2 断面交通流路径追溯过程

以大学城隧道为例进行交通流路径识别说明。选取数据质量较好的2021年6月3日8:00-9:00 数据为样本数据，RFID 显示高峰交通流为4172 辆·h-1，按1 min 周期统计出高峰小时交通流时间序列，利用TIDWT 切分时间序列并统计出平稳项，剔除噪声车辆共76 辆，有效样本车辆4096辆，如图2所示。

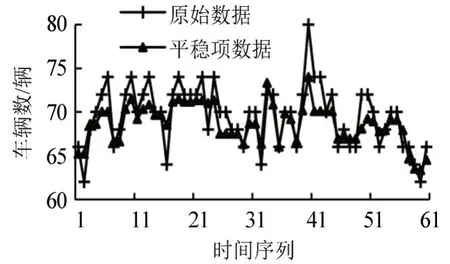
图2 TIDWT切分RFID平稳项数据Fig.2 RFID stationary item data after TIDWT

利用Transcad 二次集成开发进行基于综合成本阻抗的RPL-O-SUE 交通分配，耗时198 s，经180次迭代后，目标函数为10050031.252，RMSE 由初始1572.127 减少为0.004，MRE 由初始71.451%下降至0.498%，MRE 小于0.500，达到算法收敛判定条件，收敛过程如图3和图4所示。

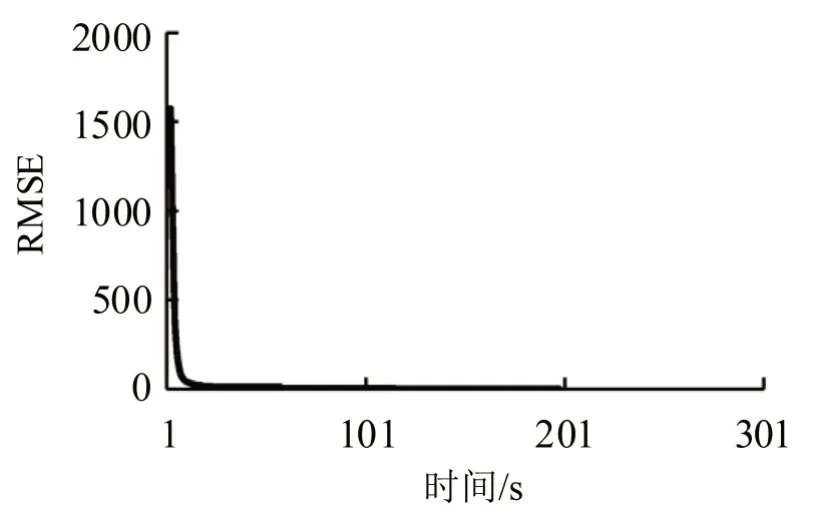
图3 改进SUE模型收敛速度示意图Fig.3 Schematic diagram of convergence speed of improved SUE model

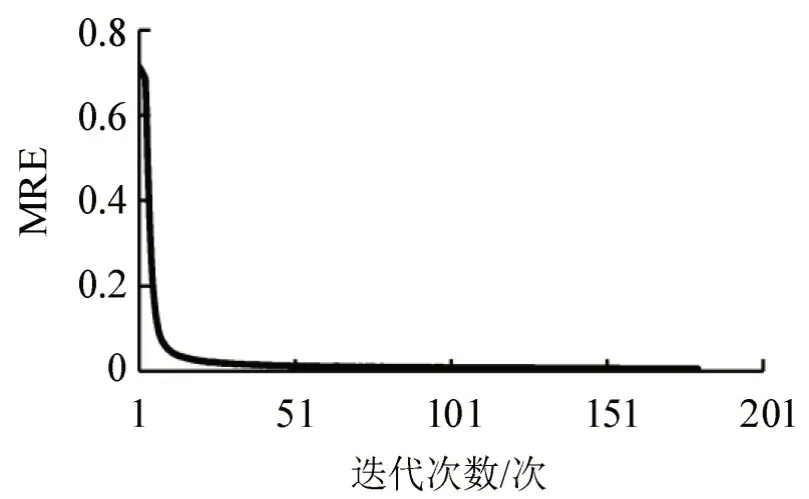
图4 改进SUE模型迭代统计示意图Fig.4 Iterative statistical diagram of improved SUE model

最终根据统计结果，单一RFID 追溯交通流主要集中在大学城隧道两侧快速路、主干路等RFID点位覆盖道路，次干路、支路等RFID未覆盖道路基本无追溯交通流，如图5所示。经过组合模型统计的路径追溯交通流呈均衡分布，次干路、支路等非RFID 覆盖路段均有追溯交通流，更加符合实际道路运行情况，如图6所示。

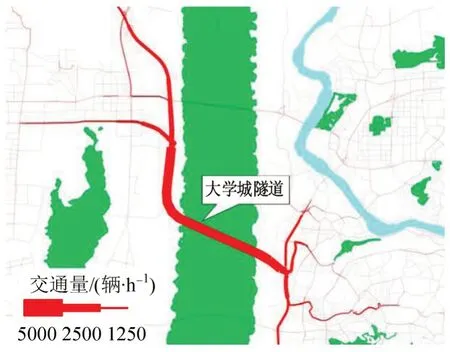
图5 大学城隧道单一RFID交通流路径追溯分析图Fig.5 Tracing analysis of traffic flow path on University City Tunnel by single RFID

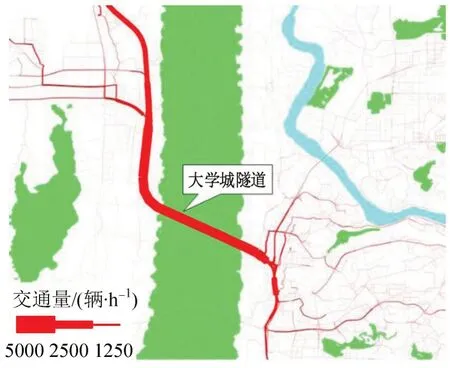
图6 大学城隧道组合模型交通流路径追溯分析图Fig.6 Tracing analysis of traffic flow path on University City Tunnel by combination model

3.3 误差精度比较

选择同日时段，通过人工车牌对比法，利用视频录像记录车牌号码信息并统计识别车辆路径，筛选出西永大道等两侧衔接道路共12 处人工监测点，其中RFID覆盖点位7处，未覆盖点位5处。

统计结果如表1所示，大学城隧道人工统计交通量为4438辆·h-1，RFID统计交通量为4172辆·h-1，较人工统计低6.0%；组合模型考虑了外地车比例，断面交通量为4464 辆·h-1，与人工统计基本一致。交通流路径识别方面：单一RFID、组合模型在RFID覆盖路段MRE分别为8.0%、6.1%；非RFID覆盖点位中，单一RFID、组合模型MRE 分别为73.6%、13.3%。组合模型在非RFID 覆盖道路具有明显优势，单一RFID 路径追溯交通量普遍低于人工统计，次支路选择倾向偏低。

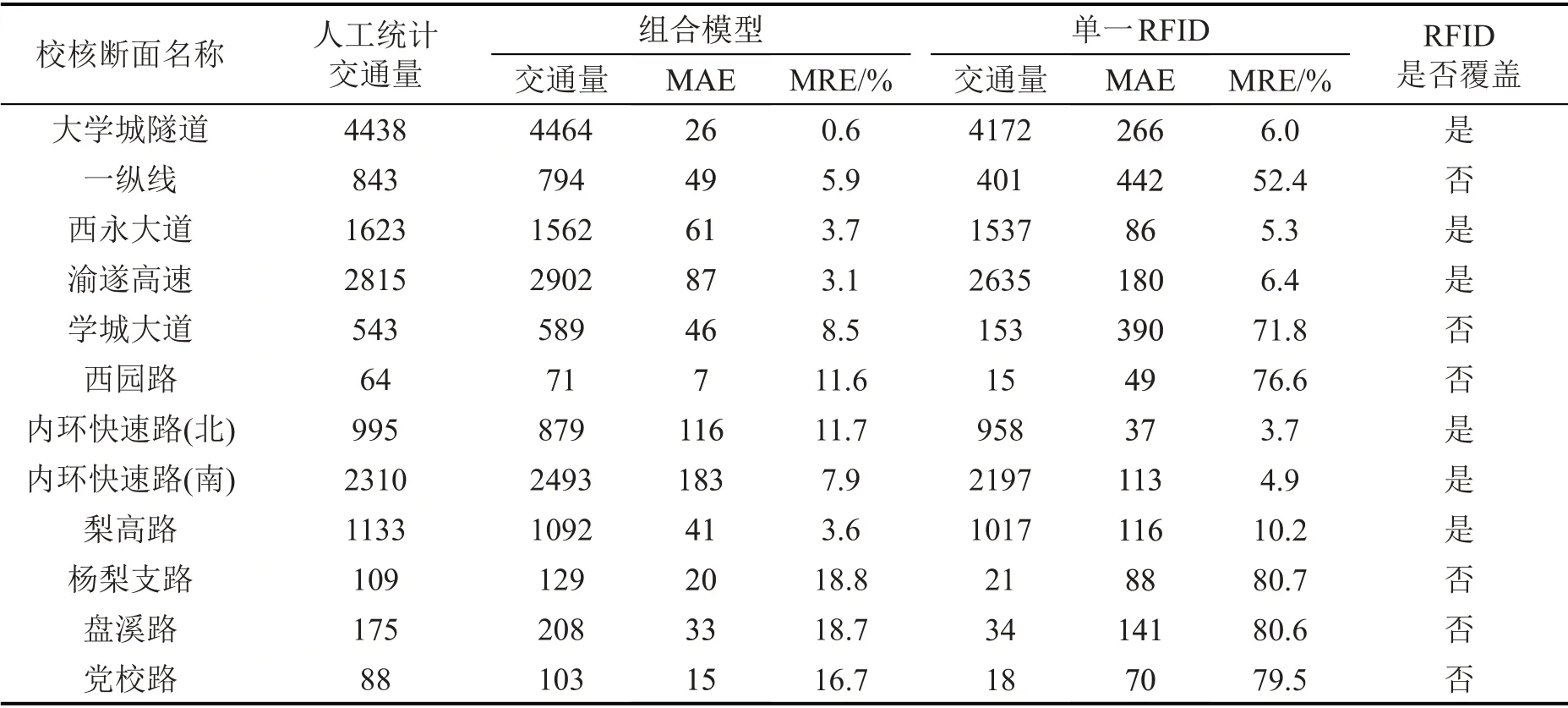
表1 大学城隧道断面交通流路径追溯分析Table 1 Details of tracing analysis of traffic flow path on University City Tunnel section

本文通过单一RFID、组合模型（TIDWT 前）误差分析验证FCD 校核有效性，通过组合模型（TIDWT 前）、组合模型误差分析验证TIDWT 数据处理效用，因此可对三者进行误差对比分析。5 条校核道路人工监测点总数量及RFID覆盖数量均一致，误差分析结果显示，组合模型MAE处于58～107辆之间，较单一RFID 下降58.5%～65.4%，较未经TIDWT 下降2.1%，MRE 处于9.2%～10.1%之间，较单一RFID 下降68.6%～76.8%，较未经TIDWT 下降2.0%，如表2 所示。单一RFID 通过模型估算的行程时间求解有效路径，实际条件下行程时间受道路条件、驾驶行为影响，致使估算行程时间与实际行程时间存在一定误差，最终导致路径识别结果与现实偏差，通过FCD 计算出的实际行程时间对模型估算行程时间进行校核修正，使之更加符合实际进而提升路径识别精度；TIDWT 通过对原始数据进行去噪处理，减少了天气、设备误差等随机事件影响，进而提高组合模型识别精度。

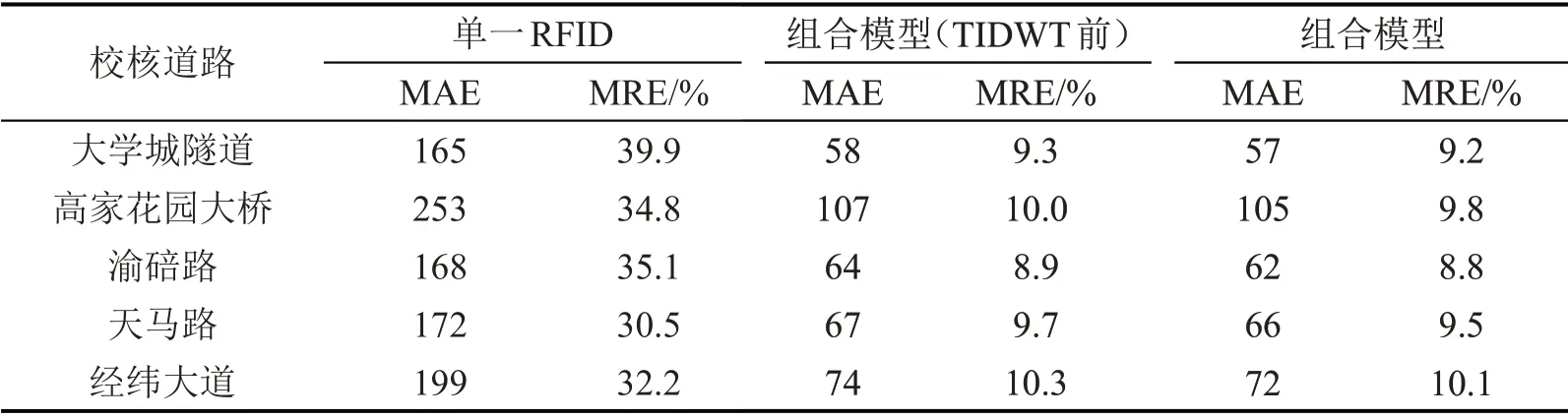
表2 模型误差明细Table 2 List of all model errors

从模型计算时间看，单一RFID 进行RPL-OSUE交通分配耗时198 s，FCD-RFID组合模型共耗时276 s，较单一RFID 耗时增加78 s，增长39.4%；与MAE、MRE 下降约60%相比，组合模型虽然耗时有一定增长，但耗时增长幅度处于可接受范围内。

在RFID是否覆盖方面，组合模型在RFID覆盖监测点位中MRE 为5.2%，此时快速路、主干路、次干路、支路识别精度基本一致，道路等级对识别精度影响较小，非覆盖监测点位为MRE13.3%，组合模型对于非覆盖监测点位仍具有较高估算精度；在不同道路等级方面，快速路、主干路、次干路、支路MRE 分别为5.7%、6.6%、8.8%、14.6%，快速路估算精度最高，估算精度随道路等级提高而提高，如图7所示。

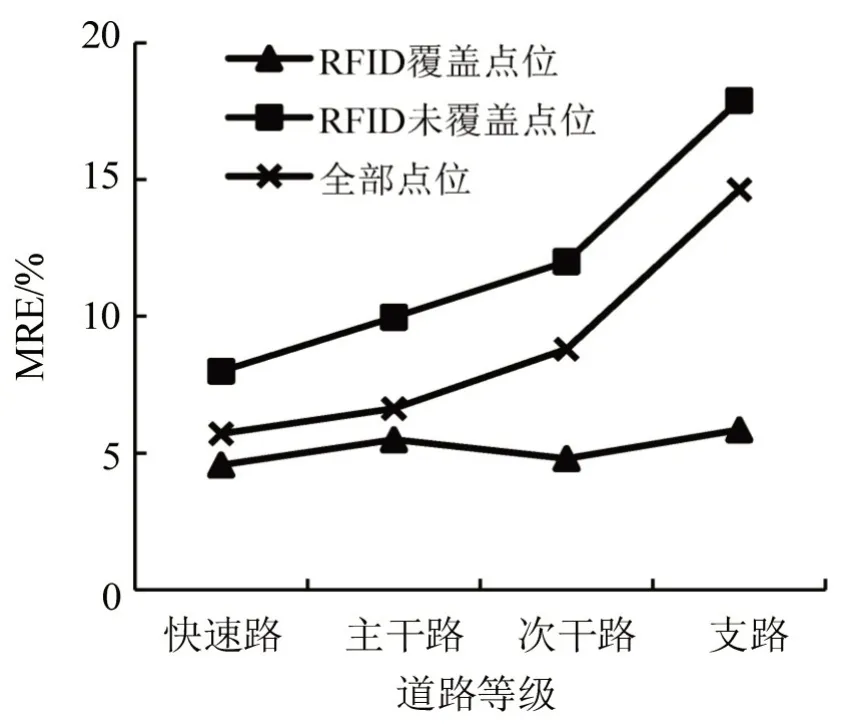
图7 组合模型不同道路等级校核路段MRE统计情况Fig.7 MRE statistics of checking road of different road grades with combined model

4 结论

本文基于RFID、FCD 等交通大数据，利用TIDWT将RFID初始数据切分为可追溯交通流、非追溯交通流及随机项这3 类，依托城市道路GIS 路网结合组合模型构建道路断面交通流路径识别体系。结果表明：

（1）组合模型对道路交通流路径识别具有较高精度，MRE 仅为9.5%，较单一RFID 路径识别误差明显下降，非RFID覆盖道路MRE为13.3%，具备良好适应性；

（2）经TIDWT切分随机项后，组合模型估算精度有进一步提升，实用性更强；

（3）FCD 数据通过校核修正估计行程时间，能有效提升交通流路径识别精度。