融合卡尔曼滤波的高速公路状态估计误差界限分析

陈喜群，曹震，莫栋

（浙江大学，建筑工程学院，杭州 310058）

0 引言

智能交通系统发展离不开大数据等先进技术的支撑[1]，随着科技进步，交通检测数据获取渠道和数据量变得越来越多，高速公路全路段交通管控需要以高质量交通状态信息为基础。由于检测器布设成本高等原因，雷达、卡口、线圈及不停车电子收费系统（Electronic Toll Collection，ETC）等高速公路检测器的空间覆盖率存在稀疏性，检测数据存在缺失。因此，从感知全路段交通状态角度分析高速公路数据质量至关重要，如何根据检测器布设方案估计全路段交通状态值得深入研究。现有研究主要集中在构建完整性、可用性、准确性及时效性的数据质量评价指标体系，利用统计和人工智能算法估计缺失数据，而在全路段交通状态估计误差界限方面存在研究不足。本文在估计误差下界[2]研究基础上，提出一种决策级融合模型，利用扩展卡尔曼滤波交通状态估计方法和平方流量误差界分析数据质量，在可用数据有限条件下，感知高速公路全路段交通状态，给出全路段特别是无检测器路段的估计误差界限，分析检测器覆盖率对估计误差上界和下界的影响效应。

1 交通流检测数据环境质量分析研究现状

数据质量分析研究涉及交通工程、统计学及概率论等多个学科，对交通流检测数据质量进行深入分析和数据修补是亟待解决的实际问题。美国交通部在交通流数据质量管理报告[3]中提出交通流数据质量评价指标体系，包括正确性、有效性、及时性、完整性、可用性和覆盖率等指标。马韵楠[4]采用模糊综合评价法构建城市交通流数据质量评价体系，基于视频检测器数据评价路段和路网数据质量。李翠翠[5]从数据有效性和完整度等方面提出数据质量问题识别方法，建立层次分析-模糊综合评价方法，从不同维度评估高速公路交通数据质量。赵盼明[6]采用两种综合评价方法评价线圈、微波、射频识别技术（Radio Frequency Identification，RFID）和视频等4种道路交通数据有效性。张程瀚[7]以城市快速路微波数据为研究对象，利用相关性检验方法分析快速路交通流时空特性，确立交通流数据质量评价体系，并利用张量理论修复交通数据。施风东[8]利用隶属度函数将改进模糊综合评价法与优劣解距离法（Technique for Order Preference by Similarity to an Ideal Solution，TOPSIS）评价法相结合，组成混合评价方法评价多源检测器速度数据质量，克服单一评价方法的局限性。

上述方法利用数据有效性和完整性等指标体系分析交通数据质量，而基于当前数据环境下交通状态估计界限的数据质量分析相关研究较少。WANG 等[2]利用Fisher 矩阵推导平方流量误差界，研究城市道路交通缺失数据的估计误差下界和达到准确估计结果的条件，解决奇异和非奇异Fisher矩阵下的缺失数据估计精度问题。这需要大量时空点位观测样本，而由于检测器布设的稀疏性，无检测器路段没有观测样本，难以进行全路段状态感知和数据环境质量分析。扩展卡尔曼滤波器是一种动态系统状态估计器，考虑系统随机噪声和检测器测量噪声，并引入宏观交通流模型，模拟交通状态演化过程。EKF 已有广泛研究，例如，WANG等[9]提出结合宏观交通流模型和测量模型的高速公路完整交通状态EKF 估计器，分析估计器跟踪能力，交通状态初始值敏感性及模型参数在线估计显著性等问题。LI等[10]认为交通流的内在随机性、模型初始条件、模型参数和模型结构不确定性会影响交通状态估计精度，提出集成学习框架提高估计精度。蒋阳升等[11]采用车联网实时数据，构建基于卡尔曼滤波的实时排队长度估计模型，解决现有排队长度估计方法不能对排队长度进行实时秒级估计的问题。因此，利用EKF机理模型拓展SFEB模型的适用范围，具有重要的研究价值。

2 SFEB-EKF决策级融合模型

构建SFEB 和EKF 决策级融合模型SFEBEKF，利用交通流模型演化机理刻画能力和有限检测数据估计全路段交通状态，基于得到的估计样本，分别采用最近邻法和SFEB 算法计算全路段交通状态，估计误差上界和下界。

2.1 估计误差下界建模

考虑共有Nl个路段的高速公路，包含Nm个检测路段和Nu个无检测器路段，Nl=Nm+Nu。以流量为例，假设Nm个检测路段中有M个正常工作检测器，θ1表示Nm-M个故障检测器路段上所有缺失的时空点位，θ2表示Nu个无检测器路段上所有未测量的时空点位，θ3表示M个正常工作检测器路段上所有的测量时空点和Nm-M个故障检测器路段上所有正常的时空数据点，即

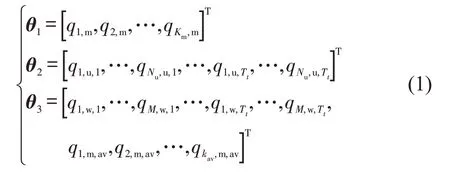
式中：qi,w,t为第i个正常工作检测器路段在t时刻的流量，i=1,2,…,M,t=1,2,…,Tt；qi,m,t为第i个故障检测器路段在t时刻的流量，i=1,2,…,Nm-M,t=1,2,…,Tt；qi,u,t为第i个无检测器路段在t时刻的流量，i=1,2,…,Nu,t=1,2,…,Tt；Tt为总的时间步长；Km和Kav分别为故障检测器的缺失数据时空点数量和正常数据时空点数量。

WANG 等[2]根据式（1）和Fisher 信息矩阵（Fisher Information Matrix，FIM）推导出定理1 和推论1，分别表示满秩Fisher矩阵和奇异Fisher矩阵下的SFEB，具体推导过程本文不再赘述，详见参考文献[2]。

定理1 当且仅当Fisher 信息矩阵Jθ,r=是一个满秩矩阵时，参数向量存在有限方差的无偏估计量。其中，A为缩放矩阵，Rε为误差协方差矩阵，Rθ为真实流量向量的协方差矩阵，为Rθ的Moore-Penrose 伪逆。假设是任一估计器关于θ的估计，则的均方误差（Mean Squared Error，MSE）满足

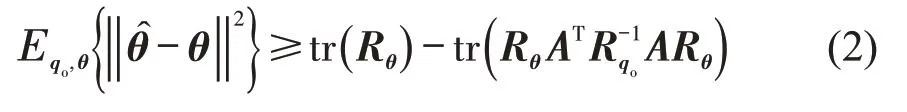
式中：qo为尺寸为[MTt+Kav]×1 的观测流量向量；θ为尺寸为[（Nm+Nu）Tt]×1的全路段整个Tt时刻的真实流量向量；A为尺寸为[MTt+Kav]×（Nm+Nu）Tt的缩放矩阵；Rqo为观测流量向量的协方差矩阵。当每对可用数据点之间没有因果关系时，A可以用观测流量向量与未知参数向量之间的互相关矩阵Rθu,qo和未知参数向量的协方差矩阵Rθu的乘积表示，则式（2）可以改写为

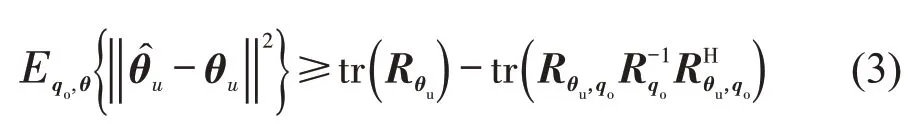
推论1 当Fisher 信息矩阵Jθ,r是奇异矩阵时，当且仅当缺失点数量小于等于Jθ,r的秩时，即（Nm+Nu）Tt-Kav-MTt≤rJ，rJ表示信息矩阵Jθ,r的秩，未知参数向量θu的无偏估计存在。估计向量的方差满足

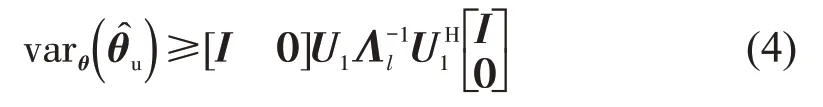
式中：I为单位矩阵；Λl和U1分别为非零特征值和对应的特征空间；若矩阵M1≥M2意味着矩阵M1-M2是半正定的。当（Nm+Nu）Tt-Kav-MTt ＞rJ时，此时无法找到无偏估计量，估计向量的方差满足

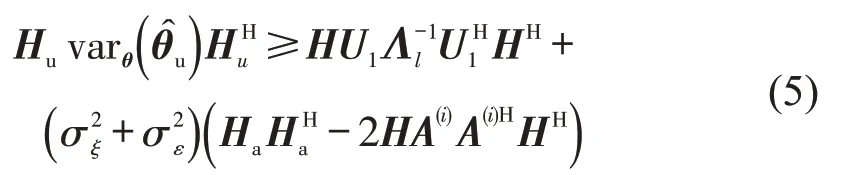
式中：H为任意缩放矩阵，行空间正交于Jθ,r零特征值对应的特征空间；Hu、Ha为H对应于θu、θa的子矩阵；θa为观测流量向量；σ2ξ和σ2ε为高斯白噪声方差。

2.2 决策级融合过程

估计误差下界计算公式，涉及协方差矩阵和互相关矩阵的计算，其中，故障检测器路段可用历史数据确定，而无检测器路段无法参与计算，因此，无法得到全路段交通状态的估计误差下界。为此，引入EKF交通状态估计模型，利用有限检测数据估计所有路段的完整状态，把无检测器路段估计值作为真实值用于计算。SFEB与EKF模型的决策级融合过程如图1所示。

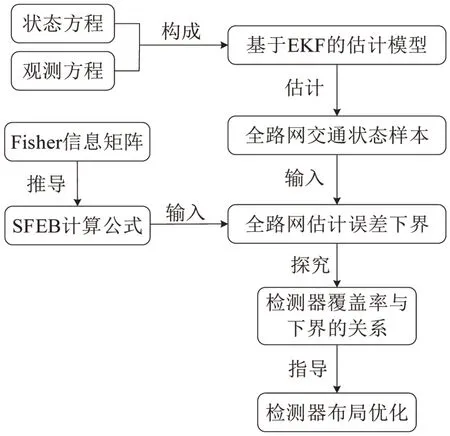
图1 SFEB-EKF模型决策级融合过程Fig.1 Decision-level fusion process of SFEB-EKF model

首先，建立状态方程和观测方程，两者共同组成EKF交通状态估计模型，计算得到全路段交通状态估计样本；在得到全路段估计样本后，将无检测器路段的估计值作为真实值输入估计误差下界计算模型中，得到高速公路全路段估计误差下界计算融合模型SFEB-EKF。一方面，该融合模型利用宏观交通流模型的机理刻画能力估计全路段交通状态，实现全路段状态感知；另一方面，在检测器空间覆盖不足情况下，计算全路段特别是无检测器路段的交通状态估计误差界限。

融合模型SFEB-EKF 可用于分析检测器空间覆盖率对估计误差界限的影响效应，在检测器空间覆盖率不足情况下，分析交通检测器数据质量，不同检测器覆盖率提供不同程度的有效状态信息，精确有效的信息越多，估计误差越小。根据感知精度与检测器覆盖率的关系，反推为实现特定估计精度，数据环境应满足的最低要求（例如，检测器覆盖路段占全路段的比例），为检测器布设方案优化提供参考。

3 高速公路应用案例

利用台湾桃园内环线高速公路开源数据测试融合模型效果，测试路段长度约为7 km，主线为单向3车道，包含上匝道和下匝道各1条，参考WANG等[9]的划分策略，将其划为15段，主线上有5个检测器L1、L2、L3、L4和L5，分别位于第1，3，6，11及15个路段，上匝道和下匝道分别布置检测器R2 和R14，如图2 所示。提取2021年1月1～31日共1 个月的数据，具体为每天13:00-21:00 间隔5 min 的流量、速度和占有率，车道交通密度ρ（t） 通过时间占有率和时变等效车长得到，即

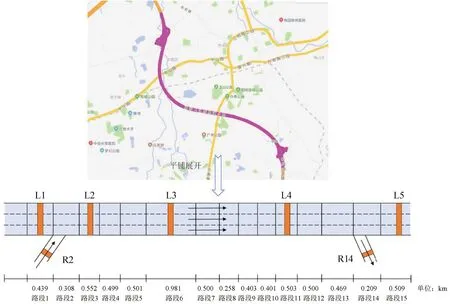
图2 高速公路位置、检测器布设位置和路段划分Fig.2 Geographic location,detectors layout,and division of road sectionsof study highway

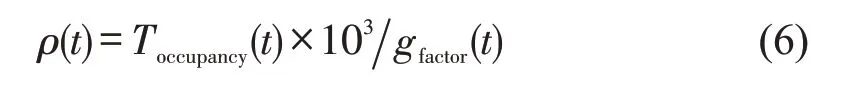
式中：Toccupancy为时间占有率；gfactor为有效车长（m）。

为分析检测器覆盖率对估计误差上界和下界的影响，对主线检测器路段进行人为缺失，共设置3种覆盖率情形，即缺失1个检测器（覆盖率为80%），缺失2 个检测器（覆盖率为60%）和缺失3 个检测器（覆盖率为40%）。由于交通流模型对边界条件的依赖性，假设上游路段（路段1）和下游路段（路段15）的流量、速度和占有率是可观测的，仅对中间路段检测器进行数据缺失测试。

采用均方误差（Mean Square Error, MSE）和均方根误差（Root Mean Square Error, RMSE）评价融合模型SFEB-EKF效果，定义为

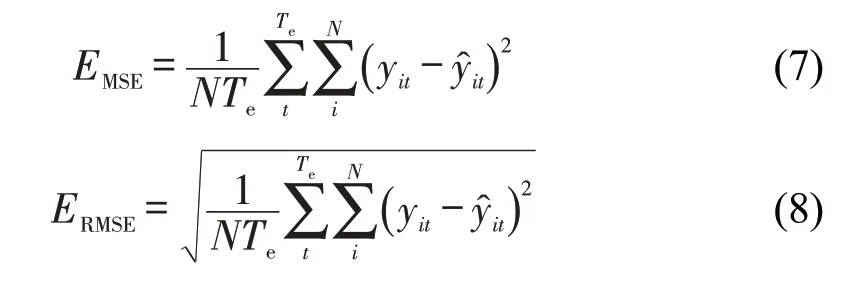
式中：N为路段数量；Te为估计的时间步长；yit和分别为路段i在t时刻的流量真实值和估计值。

分析EKF 交通状态估计结果，随机展示2021年1月27日结果，在线估计基本图参数，赋予参数初始值自由流速度vf（0）=100 km·h-1，临界密度ρc（0）=29 veh·km-1，参数α（0）=1.4。本文模型参数τ、υ、κ、δ的取值分别为17 s、5.7 km2·h-1、13 veh·（km·lane）-1、2，所有路段的参数相同。EKF模型中的随机变量采用如下标准差[9-10]：

随机展示80%覆盖率下各路段的流量、密度和速度估计结果如图3所示。

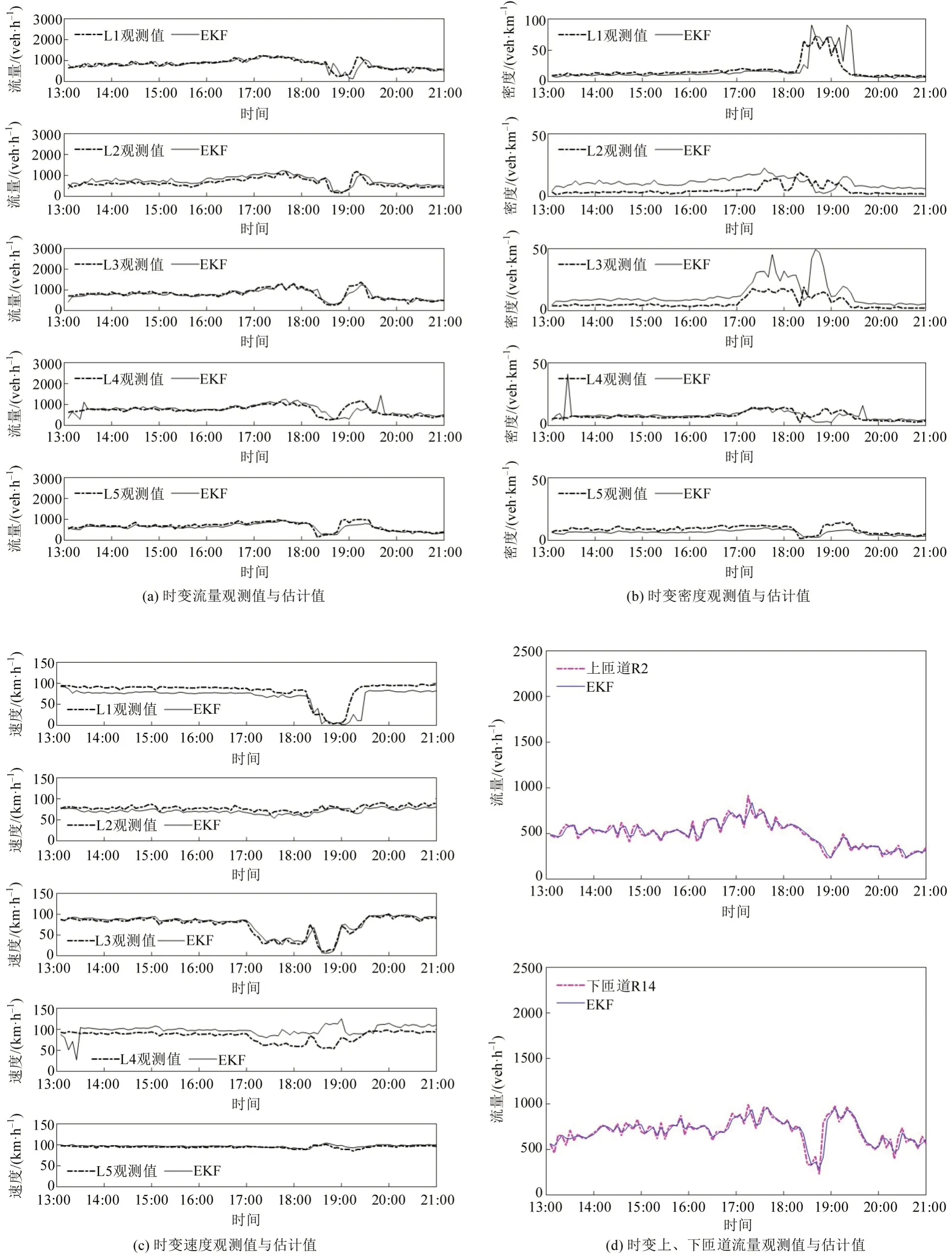
图3 检测器覆盖率80%的估计结果（以缺失L4为例）Fig.3 Estimated results of 80%detector coverage（take missing L4 as an example）

结果表明，EKF交通状态估计模型能够实时跟踪各路段的状态变化，捕捉流量、密度和速度突变，特别是晚高峰时段上匝道交通流量变大，匝道交汇区拥堵导致密度增加，速度和流量下降。

估计结果表明，覆盖率越低估计效果越差，与实际相符。估计结果存在部分估计值与观测值相差较大的情况，原因如下：一是检测数据存在误差甚至错误导致观测值没有反映真实交通状态；二是当检测器非常稀疏时，宏观交通流模型发挥主导作用，缺少观测值对纯模型估计值的修正导致估计结果不准确。整体而言，EKF估计模型在还原交通状态任务中表现良好。

在得到1月份交通状态估计样本后，测试融合模型SFEB-EKF 效果，采用最近邻法（NNM）、K 近邻法（K Nearest Neighbor，KNN）以及克里金估计（Kriging Estimator）作为对比模型。其中，NNM 是指对无检测器路段采用距离最近的检测器测量值作为目标路段估计值，该方法较为简单，适用范围广，虽然估计精度不高，但可以将其作为估计误差上界。各模型估计效果如图4所示。

图4 对比各模型估计效果，包括：SFEB 平方根、SFEB-EKF 平方根、NNM、KNN 和Kriging。在所有覆盖率下对比NNM、KNN和Kriging的误差均大于SFEB 模型，验证了SFEB 是估计误差下界。对比融合模型SFEB-EKF 和SFEB 在3 种覆盖率情况下的测试结果可以发现，两者取得相似的效果且误差保持在5%以内，其中，EKF 估计得越准，两者越接近。虽然SFEB-EKF 下界较SFEB 稍高，但仍优于其他估计器，更重要的是，SFEB无法计算无检测器路段的估计误差下界，在感知全路段交通状态时受限。而本文提出的融合模型SFEB-EKF 可以在少数检测器数据环境下，结合物理模型的优势得到高速公路所有路段的交通状态估计样本以及估计误差界限。此外，当估计误差下界越低时，说明现有检测数据越能表征全路段的隐藏共性，表示可用数据的质量越好，以此可以分析检测数据质量。

从图4中发现，不同的检测器覆盖率可实现的估计误差上界和下界是不同的，随着检测器覆盖率下降，可用的观测信息减少，估计难度增大，估计误差也变大。如果对感知精度提出一定要求，SFEBEKF可以用于指导优化检测器布设方案，从而满足相应的感知精度，例如，本文高速公路案例中，当交通管理部门对检测器布设方案进行优化时，要求实现不高于110 veh·h-1的流量估计误差ERMSE，根据SFEB-EKF结果，检测器的空间覆盖率应至少满足60%的覆盖下限。

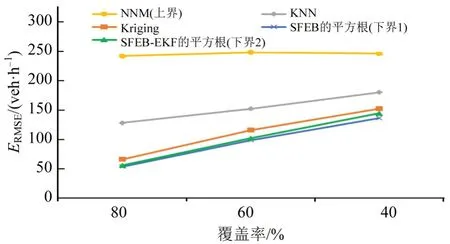
图4 融合模型SFEB-EKF与对照模型的比较Fig.4 Comparison results of fusion model SFEB-EKF with other baseline models

4 结论

本文提出决策级融合模型SFEB-EKF，利用EKF模型的估计能力感知全路段交通状态，在检测器不足环境下计算全路段交通状态估计误差下界。开源高速公路数据集实测结果表明，融合模型SFEB-EKF在缺少真实样本输入情况下，仍能取得与SFEB相似的计算结果且误差保持在5%以内，不同检测器覆盖率仿真结果显示，检测器覆盖率越高，有效信息越多，估计误差下界越低。本文提出的模型可用于计算无检测器路段以及全路段的估计误差界限，在特定的感知精度要求下为检测器布设方案提供参考。