一种优化编码信号距离副瓣的快速算法

张 磊，曹文杰，完 诚，范 宽

(中国船舶集团有限公司第八研究院，江苏 扬州 225101)

0 引 言

常见的雷达信号主要包括线性调频信号、相位编码信号、非线性调频信号等。

线性调频信号的模糊函数具有斜刀刃的特点，对多普勒不敏感，适用的场景较广，但是由于近年来电子对抗等技术的不断发展，线性调频容易被敌方侦察感知到，进而对己方干扰，反而影响对目标的探测。

相位编码信号的模糊函数是较为理想的图钉型，它的抗干扰性能比较好，常见的二相编码信号有巴克码、m序列、Gold序列等，多相编码信号有四相码、Frank码、P1码、P2码、P3码、P4码等。二相码的应用受限于码长的局限性，相比而言，多相编码具有更好的应用场景。但是由于多相编码信号的旁瓣仍然较高，容易造成多目标检测时小目标的丢失，因此相位编码信号距离旁瓣的优化问题仍然是值得研究的。

1 循环算法

1.1 副瓣电平模型

描述波形的副瓣电平指标有2种：峰值副瓣电平(PSL)和积分副瓣电平(ISL)，即：

(1)

(2)

由于峰值副瓣电平的最大副瓣位置一般是随机变化的，没有明显的规律，本文主要采用积分副瓣电平进行分析。

要使得波形的积分副瓣电平降低，即使得ISL尽量小。对于码字长度为的离散序列信号，式(2)可以表示为：

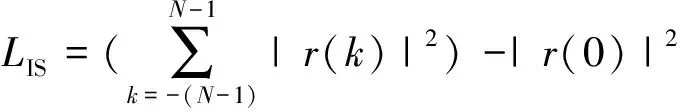
(3)

式中：()为信号的自相关函数。

为了评价积分旁瓣电平的效果，定义品质因子(MF):

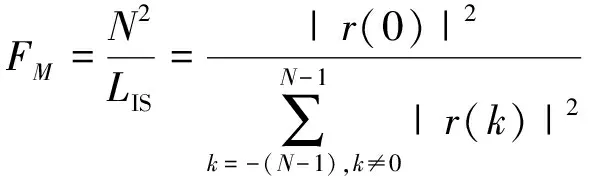
(4)

品质因子越大，代表信号的积分旁瓣电平越小。

根据帕斯瓦尔定理：

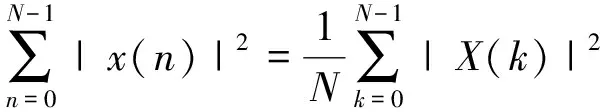
(5)

将式(3)进行转化，得到：

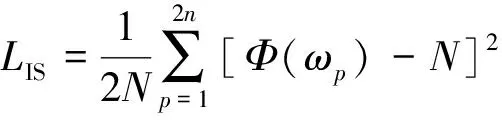
(6)

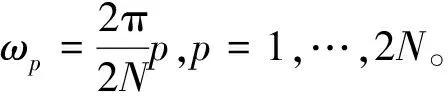
众所周知，对任意的∈[0,2π]，

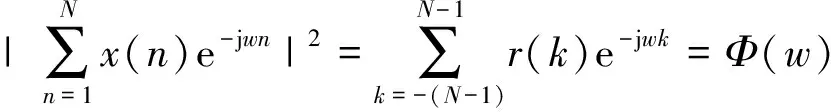
(7)

那么，式(6)转化为：

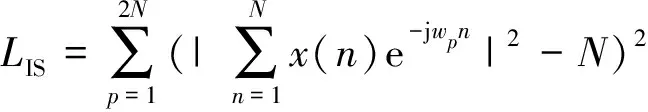
(8)

最小化积分旁瓣问题转换成使得式(8)最小的问题。

1.2 CAN算法

CAN循环算法是由Petre Stoica等提出的一种针对恒模序列的优化算法，针对式(8)，其进行了简化处理，等价于：

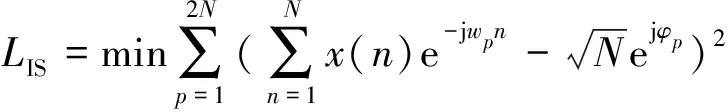
(9)

=min‖-‖

(10)

对于给定的序列()，可以得到使得式(10)最小的{}：

=arg(),=1,…,2

(11)

式中：arg表示相位，这样就得到了新的，给定的情况下，又可以得到新的()：

()=ejarg()

(12)

通过反复循环迭代直到达到设定的门限：

‖+1-‖<

(13)

循环结束，得到满足条件的优化序列。

CAN算法是一种局部优化算法，对于不同的初始序列，得到的优化结果可能是不一样的，这样对于给定的码长，可以得到一组积分旁瓣电平较低的序列，用于脉间正交码型的设计，生成多组序列，对算法的运行效率要求较高。

2 基于FFT的快速循环算法对多相编码信号的优化

2.1 Frank码模型

Frank码对应于一个线性调频信号的阶跃相位近似，脉冲分为组，每组进一步分为个子脉冲，Frank码的总长度为，Frank相位如下：

Frank码由于是对线性调频信号的近似，因此其模糊函数综合了线性调频和相位编码的特点，在特定的多普勒频率上损失较小，同时由于其未从原理上进行波形设计，因此Frank码仍有进一步优化的空间。

码长=144时，Frank码的时域波形图如图1所示，波形的零多普勒图如图2所示。

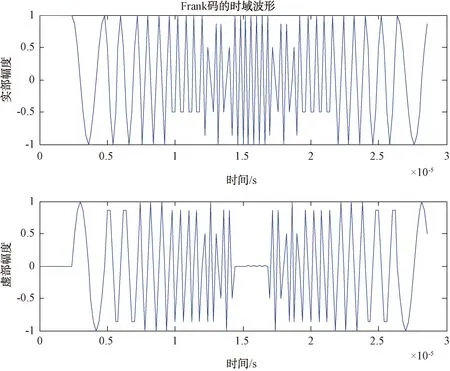
图1 码长144的Frank码时域波形图

图2 码长144的Frank码零多普勒图

2.2 基于FFT的快速循环算法流程

观察矩阵以及式(11)，实际上式(11)可以等价于对的快速傅里叶变换后求相位值，同时，观察式(12)，可以等价于对的逆傅里叶变化后求相位，再构造指数生成新的序列()。那么基于FFT的快速循环算法流程可以用图3表示。

图3 基于FFT的快速循环算法流程图

3 仿真分析

3.1 采用快速循环算法优化的结果

仿真参数：Frank码码长144，快速循环算法门限值0.001。优化前后波形的距离副瓣图如图4所示。

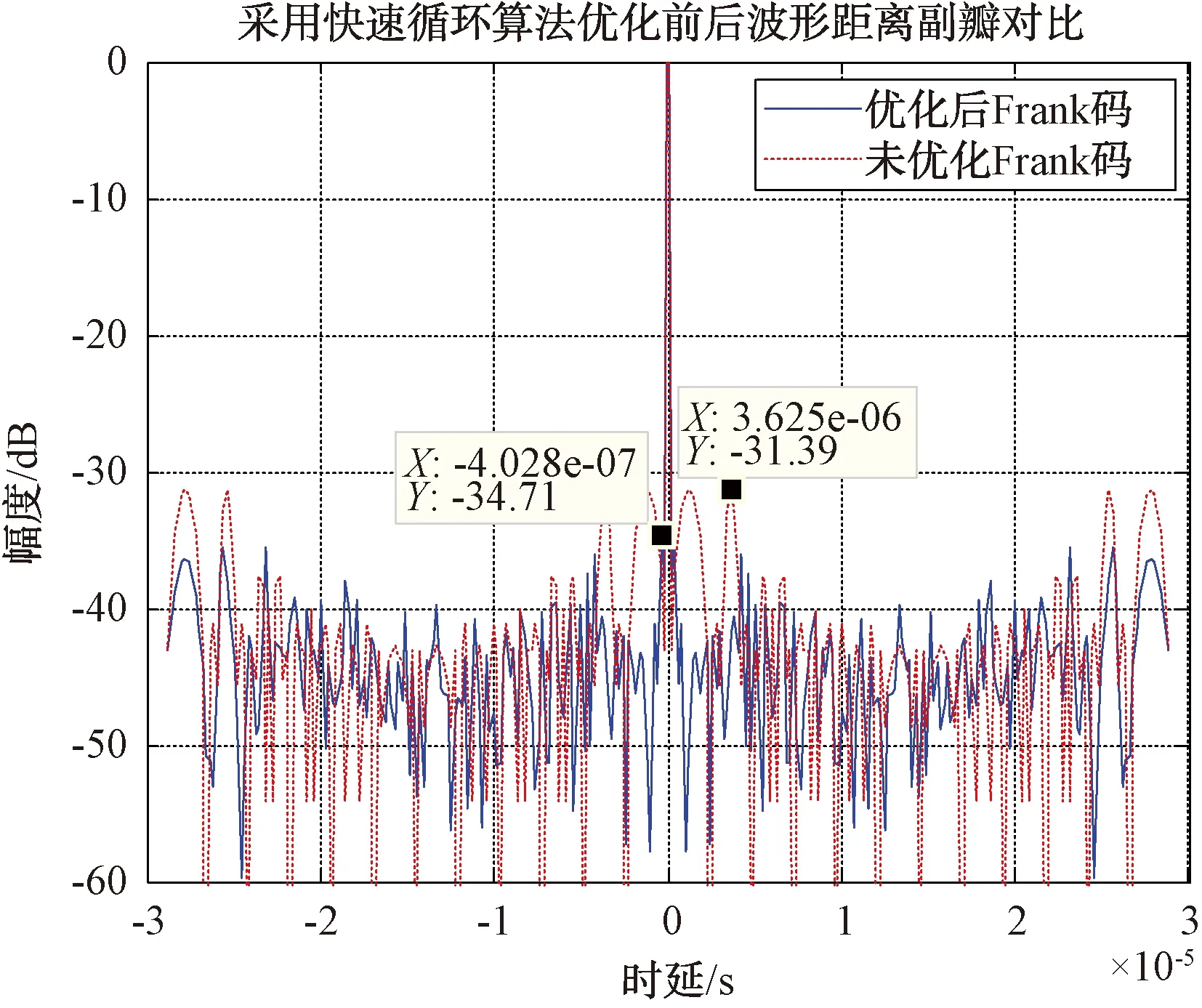
图4 采用快速循环算法优化前后距离副瓣图

可以看到，优化前后Frank码的距离副瓣由-31.39 dB优化为-34.71 dB，计算优化前后的品质因子，由28.159提升为61.475。这里只是用最大旁瓣来对比，实际有可能最大旁瓣未必优化，因为CAN模型只是针对积分旁瓣电平，所以用品质因子描述更为合适。

3.2 不同码长下的品质因子的变化

仿真参数：快速循环算法门限值0.001，Frank码码长[49,64,81,100,121,144,169,196,225]。采用快速循环算法优化前后波形的品质因子的变化如图5所示。

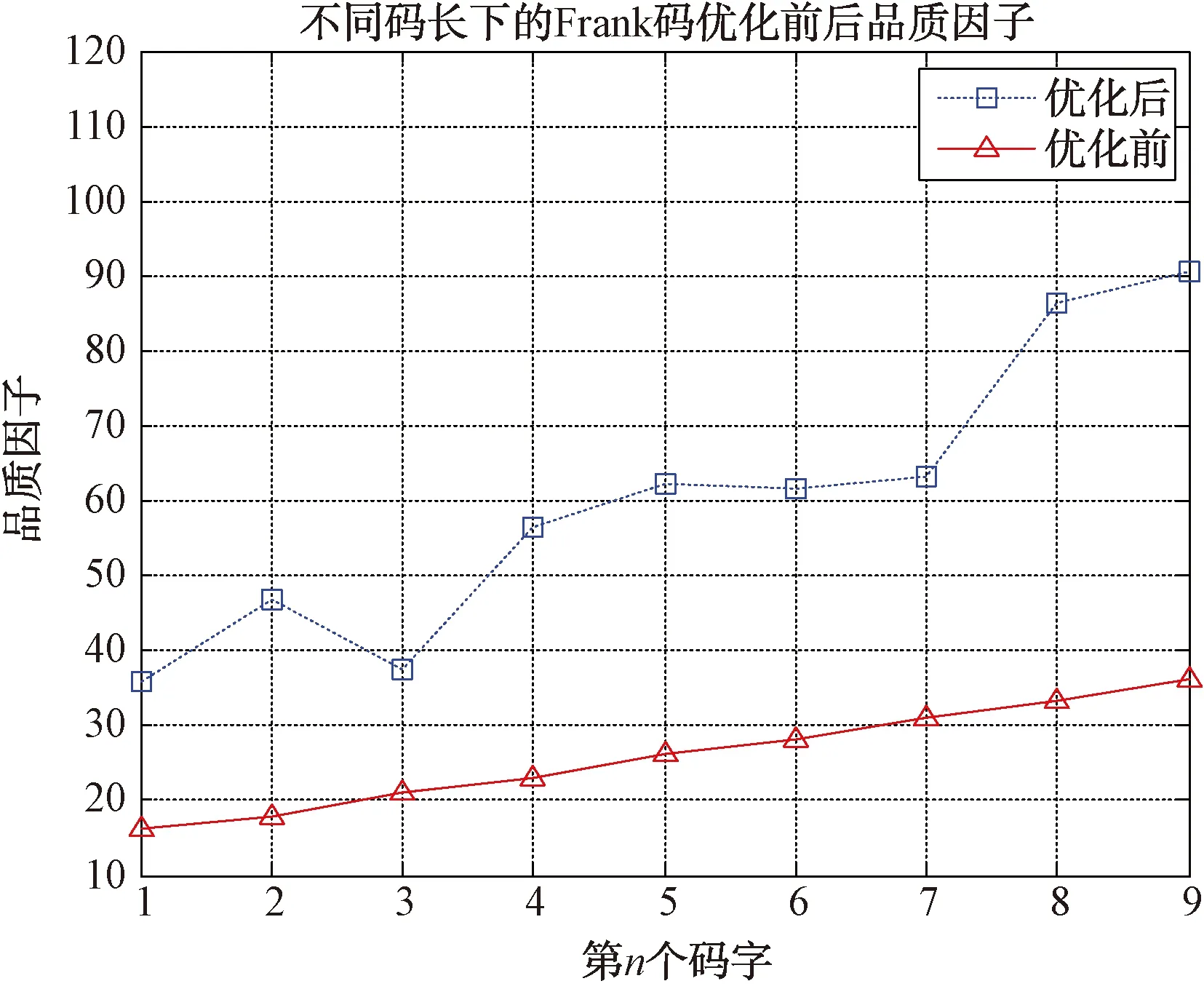
图5 不同码长下的Frank码优化前后品质因子图

采用快速循环算法优化后的波形相比Frank码品质因子有了明显的提升。

3.3 不同门限下的品质因子的变化

仿真参数：Frank码码长[49,64,81,100,121,144,169,196,225]，门限[0.1,0.01,0.001,0.000 1]。采用快速循环算法优化后波形的品质因子随码长变化如图6所示。

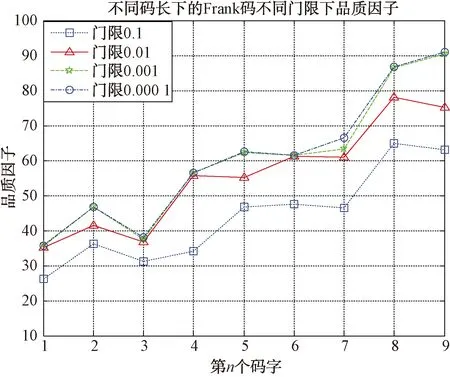
图6 不同门限下的Frank码优化后品质因子图

门限从0.1变为0.001时，品质因子有显著提升，但是从0.001变为0.000 1时，品质因子变化较小，循环算法的迭代次数也显著增加。

3.4 采用FFT和不采用FFT运行效率对比

仿真环境如下：计算机配置为Intel(R)Core(TM)i5-4590 CPU@3.30 GHz，内存4 GB，仿真软件采用matlab R2014a，门限选择0.001，Frank码码长[49,64,81,100,121,144,169,196,225],采用FFT和不采用FFT分别对不同长度的frank码进行波形优化，对比找到局部最优值的时间，结果如图7所示。

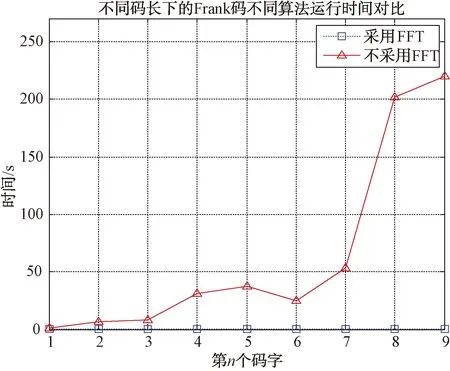
图7 不同码长下不同算法运行时间

由于不同码长下循环迭代的次数不一样，因此用运行时间除以迭代次数更加能够说明快速算法的效果，如图8所示。

图8 不同码长下单次算法运行时间

由图8可知，采用FFT可以大幅缩小算法运行的时间，在码长255时，采用FFT运行的时间为0.198 s，而不采用FFT所需的时间为219.672 s，2种方法的迭代次数都是2 023次。随着码长越大，不采用FFT的算法时间呈指数级增长，这是难以接受的，因此采用FFT可以大幅缩减波形优化的时间。

3.5 量化效应对品质因子的影响

上述算法得到的离散序列的相位可能是[0,2π]的任意值，然而实际应用中，相位值一般只能达到2，这样实际信号的品质因子会恶化，不同码长下的量化前后的品质因子变化如图9所示。

仿真参数：快速循环算法门限值0.001，量化位数分别为5位、6位、7位、8位。考虑量化和不考虑量化波形的品质因子随着码长变化曲线如图9所示。

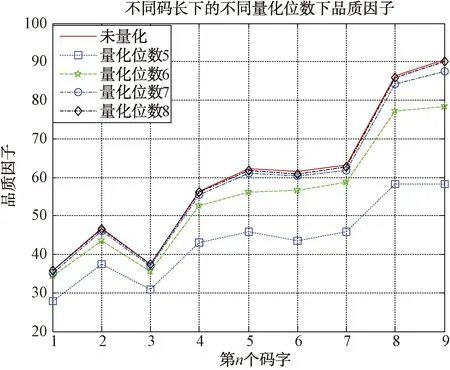
图9 不同码长下不同量化位数波形品质因子

可以看到，量化位数为5、6时，量化效应导致的品质因子恶化明显，量化位数为7、8时，量化效应不明显，所以在实际应用中应尽量提升量化的位数，这样波形的性能受量化效应的影响较小。

4 结束语

波形的距离副瓣是波形设计的一个重要指标，本文构建了积分旁瓣最小化模型，采用快速循环算法进行优化求解，但是实际波形使用中，除了考虑波形的距离副瓣，波形的多普勒容限也是需要关注的，因此，给定多普勒容限和距离副瓣条件下的波形优化设计是后续改进算法设计的目标。