基于深度神经网络优化的机械运行特征识别与分类

陈玉苗

(合肥共达职业技术学院，合肥 231135)

0 引言

机械在运行过程中其稳定性受环境影响较为严重，时常因某个零件发生故障而干扰整机工作运行效率。如何使用高性能检测技术，监测机械运行状态、诊断运行故障，一直是机械研究领域的重点课题。近年来深度神经网络在故障诊断领域得到了广泛的应用与推广，传统的深度神经网络隐含层数不足、损失函数约束性低等问题往往导致机械运行特征识别效果不佳[1]。为此，本文采用改进的稀疏自编码器构建深度神经网络模型，构建包含4层稀疏自编码器的深度神经网络，用于高精度识别运行特征以判断机械运行状态。

文中机械运行信号采集自精密零件滚动轴承，滚动轴承实现了运转中轴与轴座产生的滑动摩擦向滚动摩擦的转换，通过减少摩擦损失来优化机械运行效率[2]的作用。预先识别机械滚动轴承运行特征发现故障问题，对于减少精密零件损坏意义重大。

1 基于深度神经网络优化的机械运行特征识别方法

1.1 基于小波变换的机械运行信号时频分析

精密零件滚动轴承运行数据采集完毕，首先使用谐波算法去除原始信号中的谐波分量，然后使用小波变换提取机械信号的时频特征生成时频分析图[3]。小波变换基于机械运行信号高频与低频特征确定其窗口的尺寸，具有较强的信号特征适应性，分析机械运行时频特征的精确度较高。

定义机械精密零件滚动轴承的分析信号为x(t)，对信号进行连续小波变换，方法如下：

公式⑴中，设定尺度因子λ与平移因子μ，前者用于调节小波函数的伸缩，与频率相对应；后者对应的是时间变量，调节小波函数位于时间轴上的位置，λ、μ值均为连续的变量。ψ*(t)是ψ(t)的复函数。

本文构建基于改进稀疏自编码器的深度神经网络，使用小波变换算法可生成机械运行信号的时频分析图，构建深度神经网络对信号特征进行分类，以识别机械运行的状态。输入机械运行的时频分析图得到机械运行状态类别。

1.2 基于改进稀疏自编码器的深度神经网络优化

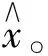
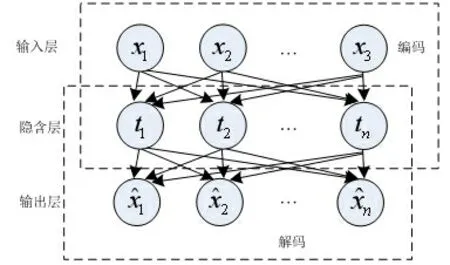
图1 自编码器结构

采用优化交叉熵作为损失函数，公式⑵为交叉熵损失函数表达式：

稀疏自编码器是赋予自编码器隐含层稀疏约束，为自编码损失函数施加稀疏惩罚项，以学习到稀疏特征，避免构建的深度神经网络过度拟合。具体方法是在网络训练期间加入权重衰减项与稀疏正则化项[6]，分别采用G、M表示，改进后交叉熵损失函数表达式为：

公式⑶中，权重衰减、稀疏化参数分别用ψ、β表示。参数G可以维持权重衰减处于较小状态，避免大权重带来的映射平滑[7]；参数M有助于增强相关机械运行特征的泛化水平。

本文构建的系数自编码器包含4个隐含层，首个隐含层输出即为首个编码器的输出，其表达式为：

公式⑷中，W1、b1分别表示首个编码器的权重矩阵、偏置值；首个编码器的值作为第二个编码器的输入，以此类推末端(第四层)解码器输出即为t4=η(W4t3+b4)，网络的最终输出结果y4=η(W4t3+b4)。

1.3 基于优化深度神经网络的机械运行特征识别与分类

采用优化后的稀疏自编码器构建高精度的深度神经网络，用于分类机械滚动轴承运行信号的特征，识别机械运行状态。本文稀疏自编码器由含4个稀疏自编码器堆叠而成，Softmax分类器与隐含层末端输出层相连接，由此构建的深度神经网络优化模型见图2。

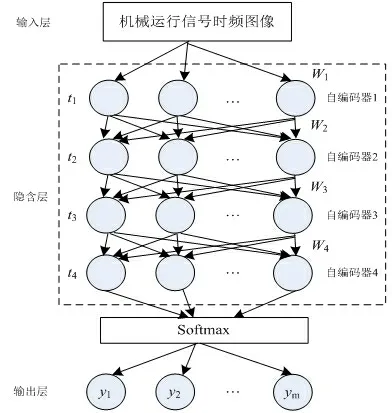
图2 基于稀疏自编码器的深度神经网络优化模型

滚动轴承运行状态包括故障与正常两种状态，常见故障有裂纹故障、烧伤故障、振动异常、接触面损伤。深度神经网络优化模型识别机械运行信号特征步骤如下：首先利用小波变换算法生成机械运行信号的时频图像；然后将图像作为样本输入训练完成具有合理参数的网络，由隐含层的优化稀疏自编码器提取时频图像的特征[8]，根据图像特征归类机械运行状态所属类型输出。

2 实验与分析

在实验室搭建滚动轴承运行测试平台，用于开展机械运行特征识别与分类测试，以径向方式采集机械运行信号，信号采样点布置在滚动轴承支撑结构外部、加载轴承、试验台面三个关键位置；采样过程中选择最低两个周期的采样长度，以确保各个数据样本包含的机械故障运行数据趋近完整。测试共采集到5组机械运行信号，其中包含4组故障信号(裂纹故障、烧伤故障、振动异常、接触面损伤)与1组正常运行信号，每组信号包含70组数据。70%采集样本作为训练数据集，30%样本作为测试数据集验证深度神经网络识别机械运行特征的性能。

采集机械滚动轴承运行信号后使用谐波去除算法滤除谐波分量，基于小波变换算法获取机械运行的时频图像作为深度神经网络的输入，输出结果即为机械运行特征的类型，描述了机械运行的所属状态。为了突出本文方法在机械运行特征识别领域的优势，与采用自编码深度神经网络模型(方法1)、稀疏自编码神经网络模型(方法2)进行对比测试。方法1和方法2识别分类机械运行特征的过程与本文方法基本一致，都是运用深度神经网络构建识别模型，不同的是：方法1采用自编码器构建深度神经网络识别模型过程中采用传统的自编码器，没有对自编码器进行稀疏处理，本文方法为深度神经网络的交叉熵损失函数增加了权重衰减项与稀疏正则化项，实现自编码器稀疏约束；方法2在方法1基础上对自编码器的损失函数做了初步稀疏处理，但仅仅增加了稀疏正则化项，和本文方法相比稀疏处理不够全面，本文方法在传统损失函数的基础上采用了交叉熵形式的损失函数。

2.1 稀疏自编码器层数对机械运行特征识别的影响

稀疏自编码器数量影响模型识别效果，为了保证本文构建的深度神经网络模型识别机械运行状态效果最佳，使用不同层数的稀疏自编码器网络进行测试，稀疏自编码器数量取值为1、2、3、4、5，在此基础上基于测试集进行测试，识别准确率如图3所示。

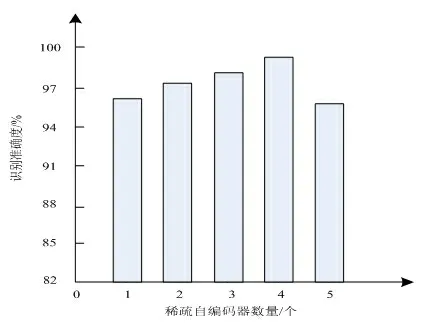
图3 不同稀疏自编码器下的模型识别准确度

分析图3可知，不同数量的稀疏自编码器对应的机械运行特征识别准确度均达到了95%以上，总体来说构建的深度神经网络识别率都达到良好水平。具体分析可知，随着稀疏自编码器数量的变化识别精度出现了先增加再降低的趋势，稀疏自编码器数量为4层时，识别机械运行特征准确度达到了峰值99.2%，当稀疏自编码器再次增加时对应的识别准确度仅为95.6%，识别效果出现大幅度波动，下降幅值较大。所以，当稀疏自编码器数量取值为4层时取得的机械运行特征识别效果最佳，说明本文构建的4层稀疏自编码器深度神经网络性能较优。

2.2 改进深度神经网络平均识别误差分析

本文方法以及另外两种对比方法的机械运行特征识别与分类的相对误差如表1所示。

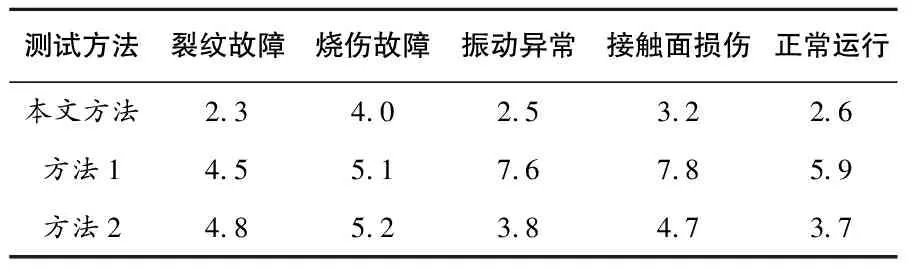
表1 三种方法的机械运行特征识别与分类的相对误差 /%

通过表1数据可知，本文方法识别滚动轴承运行特征的相对误差区间为2.3%～4.0%，识别机械裂纹故障特征的相对误差最低仅为2.3%，识别烧伤故障特征的误差最高，仍没有超过5%；相比之下，方法1的最低识别误差为4.5%，识别机械接触面损伤特征的误差最大，可达7.8%；方法2识别机械运作特征的误差在3.7%～5.2%之间。总体而言，本文方法识别5种机械运行特征的精度最高且较为稳定。

“振动异常”故障是较为常见的机械运行问题，为了明确各方法识别“振动异常”故障的具体情况、掌握各方法的详细性能，统计了三种方法在70组实验数据上的识别误差表现，如表2所示。

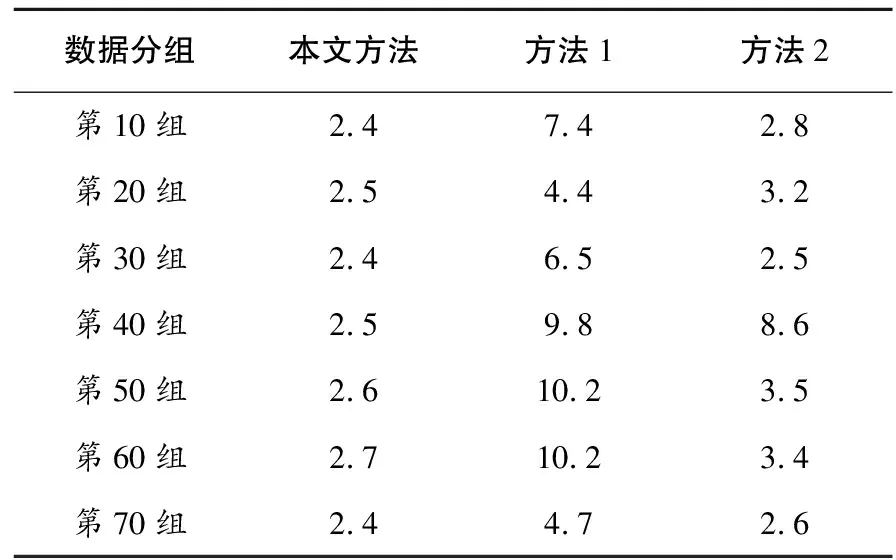
表2 各方法在“振动异常”故障数据上的误差统计 /%

分析表2数据可知，本文方法识别并分类“振动异常”机械运行特征的误差范围为2.4%～2.7%，误差波动较小、识别机械运行特征的性能较为稳定；方法1识别并分类“振动异常”机械运行特征的最大误差高达10.2%，并且出现了两次，最小误差为4.4%，波动范围较大且稳定性差，不适合投入实际应用；另外，方法2识别“振动异常”故障的平均误差虽小，但也出现误差波动较大的情况，识别效果也不理想。

相比方法1而言，本文方法利用稀疏自编码器构建深度神经网络，对自编码器进行稀疏约束，所以取得更优的机械运行特征分类效果；相比方法2而言，本文方法在交叉熵损失函数中加入权重衰减项与稀疏正则化项，方法2仅仅进行了稀疏处理，并未添加权重衰减项，因此本文方法很好地对权重进行合理约束，由此降低机械运作特征识别的误差。

3 结论

本文基于改进稀疏自编码器构建深度神经网络模型，在网络交叉熵损失函数中加入权重衰减项与稀疏正则化项，用于识别精密零件滚动轴承运行特征，判断机械的运行状态。机械运行特征识别与分类测试结果显示，4层改进稀疏自编码器构建的深度神经网络识别效果最优，有效提升滚动轴承特征识别的精度，识别稳定性较为理想。未来关于深度神经网络在机械运行特征识别中的应用研究，可着眼于网络的 Softmax 分类器改进领域，进一步提升机械运行特征识别与分类的效果及性能。