人行景观斜拉桥舒适度研究

尹栋佳 聂科琴 刘政伟

(湖北省交通规划设计院股份有限公司 武汉 430051)

随着景观性人行桥梁的兴起，国内外轻柔型结构桥梁大量涌现。其中斜拉桥和悬索桥也是人行桥梁的典型桥型。为避免人、桥共振，减少行人的不安全感，现行规范要求人行天桥上部结构竖向自振频率不小于3 Hz[1]。

在工程实践中，斜拉桥与悬索桥等柔性结构，结构自振频率通常难以满足规范要求。规范仅从自振频率对结构提出要求，无法保证设计的合理性与有效性[2-3]。研究表明，宜以舒适度评价作为判定人行桥结构设计是否合理的舒适性指标[4-5]。

本文结合某人行景观斜拉桥设计工程实例，对桥梁人致振动舒适度进行计算分析，验证舒适度指标对于柔性结构设计的合理性。

1 工程概况

某桥梁景观效果图见图1。

图1 桥梁景观效果图

该人行景观斜拉桥主跨88 m，结构形式为岩锚式双索面单侧张拉斜拉桥，桥宽5.0 m，有效通行宽度3.2 m。桥梁横亘在2座山岩之间，桥梁充分利用良好地质条件，斜拉索通过岩锚嵌固在山体岩石内，两侧顺接悬臂式人行梯道。斜拉索采用空间散索设计，有效提高了桥梁横向刚度，解决结构横向稳定性问题。

为有效提高结构整体刚度，斜拉索采用19根直径15.2 mm整束挤压式钢绞线，抗拉强度不小于1 860 MPa，斜拉索截面面积远大于强度所需尺寸。斜拉索采用空间平行布置，间距6 m，共12对。主梁采用钢-混组合梁，钢主梁采用Q345qD钢材焊接成框架，桥面板采用8 cm厚的活性粉末混凝土预制板，通过剪力钉现浇接缝与钢梁相结合。图2为桥梁的总体布置图，图3为桥梁在斜拉索锚固区的横断面图。

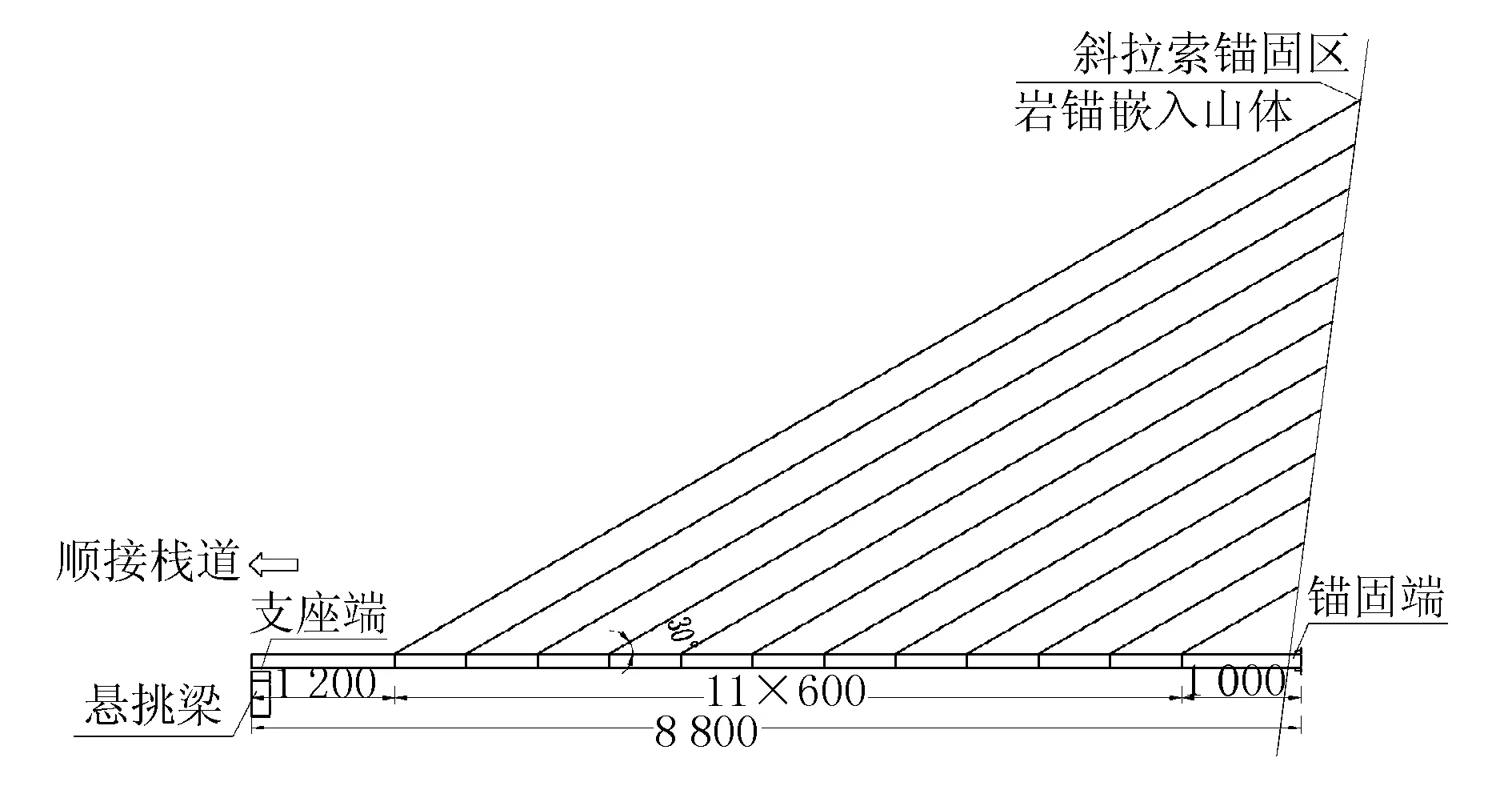
图2 桥梁布置图(单位：cm)

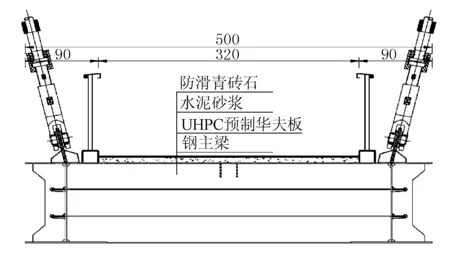
图3 主梁横断面构造图(单位：cm)

2 人行桥振动舒适性评价指标

人行桥在步行荷载下的反应是由激励条件、结构刚度、质量、阻尼等多种因素控制。人行桥的舒适感指的是人对结构振动感觉钝化。结构振动方向、振动频率、振动响应振幅等因素都会对人体舒适感觉产生影响，均可以作为振动程度的评价指标。对比分析国外人行桥舒适度评价标准和规范发现，限制动力响应值法相比频率调整法更适合大跨轻柔人行桥结构设计，是最为常用的评价指标[6]。我国《建筑楼盖结构振动舒适度技术标准》[7]是国内首部以结构动力响应值法评价结构舒适度的行业标准。

2.1 人行激励荷载

随机激励由于人行荷载的随机性，只能用少数几个样本来描述整个随机过程，分析结果只能代表整个分析空间的一部分。一般情况下，人行运动是杂乱无章的，但大量行人的运动叠加可以在结构的竖向和横向产生规律性的周期特点。根据ISO 10137《结构设计基础建筑物抗振使用性》规范中规定，单人行走的竖向荷载模型，对单足落步进行周期性叠加并考虑一定的重叠时间，按傅里叶级数的形式表示如下。

F(t)=P[1+∑αicos (2πifst+φi)]

(1)

式中：F(t)为单人行走竖向荷载的时间函数；P为人的自重，N；αi为第i阶荷载谐波的动载因子；fs为步频,Hz；t为时间,s；φi为相位角。

研究表明[8-9]，人行激励下结构的第一振型谐波起控制作用。为了简化模型，采用第一阶荷载谐波来模拟人行激励荷载。德国EN03规范将行人激励模拟为均布谐波荷载，将行人步频范围内的结构自振频率作为行人激励频率。基于行人流统计规律，给定竖向和侧向的行人激励荷载如下。

pv(t)=280cos(2πfvt)·n′·ψv

(2)

ph(t)=35cos(2πfht)·n′·ψh

(3)

式中：pv(t)、ph(t)分别为竖向和侧向的行人激励荷载，N；fv、fh分别为结构竖向和侧向的第一阶模态频率,Hz；n′为行人流等效人数；ψv、ψh分别为落脚频率接近结构频率的竖向、侧向概率折减系数。

人流量等效人数与交通量等级和行人密度有关，德国EN03规范[9]将其分为5类，参数见表1。

表1 行人交通等级和密度

人行激励荷载按照傅里叶级数展开后，其竖向荷载的一阶和二阶谐波频率为1.25 ～4.6 Hz，侧向荷载的一阶谐波频率基本处于0.5～1.2 Hz。参考表2所示各国规范规定的敏感频率范围，认为上述范围易引起结构共振，引起行人的不适感。

表2 国内外规范敏感频率范围 Hz

由表2可见，各国主要规范均对竖向敏感频率做了规定，对于侧向敏感频率的规定较少。但事实上，人类由于生活习惯，对于侧向共振比竖向共振的不适性更高，应当引起设计者重视，德国规范对此做出了明确规定。双主梁结构的扭转可以分解为两片主梁结构有规律地竖向振动。

2.2 振动舒适度评价标准

人致振动舒适度分析包含2方面的内容：①研究人在桥上周期性行走的激励作用，②研究桥梁结构在此激励作用下的动力响应[10]。德国EN03规范以峰值加速度作为舒适度评价指标，并明确不同舒适度等级下的竖向和侧向峰值加速度限值，取值见表3。

表3 德国规范舒适度评价指标 m/s2

3 人行桥舒适度计算

3.1 结构自振频率计算

利用midas Civil有限元软件建立该人行景观斜拉桥模型，采用只受拉桁架单元模拟斜拉索，采用梁单元模拟钢结构纵、横梁，桥面板和其他附属结构以分布荷载形式加载在模型上。桥梁模型见图4。

图4 斜拉桥有限元模型

采用Lanczos特征值向量法对结构进行动力特性分析，该桥前几阶主要振型见图5，自振特性参数见表4。

图5 主梁振动模态

表4 结构动力特性计算结果

计算结果表明，桥梁第一阶侧向振动频率为1.668 Hz，大于敏感频率上限1.2 Hz，说明该桥侧向振动舒适度良好，不需再进行舒适度分析。桥梁第一阶竖向振动频率为2.125 Hz，落在敏感频率范围内，需要进行竖向舒适度分析。

3.2 竖向振动舒适度分析

采用线性时程动力分析直接积分法分别计算结构在TC1～TC5交通流下的一阶谐波振动的峰值加速度。

桥梁结构内部衰减的机理比较复杂，无法精确计算，参数取值对于结果影响很大。根据EN03规范，钢结构在小振动下的平均阻尼比取0.004，混凝土材料取0.013，斜拉索采用钢材阻尼比取为0.004。时程分析步长在规范中未明确规定，取行人正常行走步长周期0.2～0.6 s，计算采用时程加载函数周期的1/10，即0.047 s。

桥梁结构在一阶竖向振型中的位移最大节点即为峰值加速度节点。在midas Civil软件中，可以通过包络的方式找到结构的最大峰值加速度及其节点，在TC2等级下的桥梁结构峰值加速度为0.424 m/s2，计算结果见图6。

图6 TC2荷载等级下典型节点的加速度包络图

不同荷载等级下的峰值加速度计算结果见表5。

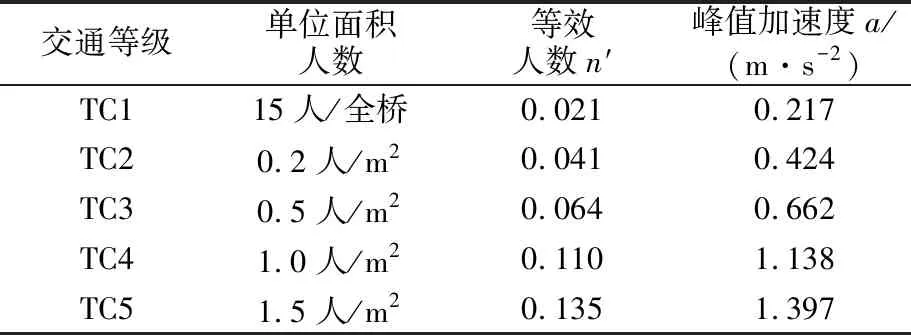
表5 不同交通流下峰值加速度

上述结果表明，峰值加速度与等效人数n′成正比，在TC1和TC2交通流下，结构舒适度为“优”，在TC3交通流下，结构舒适度为“良”，在TC4和TC5交通流下，结构舒适度为“中”，均在德国EN03规范容许范围内。当人流量<0.85人/m2时(人流交通介于正常与拥挤状态之间)，行人舒适度优良(峰值加速度<1.0 m/s2)。

4 结语

1) 人行斜拉桥等大跨轻柔结构的自重轻，自振频率低，仅仅采用现行规范推荐的频率调整法，其合理性不足；当其自振频率超出必要限值时，可通过计算结构动力响应评价行人舒适度。建议参考德国人行桥设计指南EN03进行人行舒适度验算。

2) 人行激励下桥梁峰值加速度与等效人数成正比，舒适度与人流量负相关，控制人流量可以使桥梁通行体验处于舒适区间。大跨轻柔人行天桥在运营阶段应注意对人流进行限制。

3) 本文研究的主跨88 m人行景观斜拉桥分析结果表明，竖向一阶振型频率小于3 Hz，但舒适度计算结果良好，在人流量<0.85人/m2时，行人舒适度优良。当人流量<1.5人/m2时，行人舒适度为中。

4) 斜拉桥等多次超静定桥梁的动力特性是非常复杂的，舒适度分析过程中存在诸多假定条件，与实桥存在一定差异。成桥后，可通过人为激励响应试验，对桥梁舒适度进行验证。