神经网络可信性的形式化验证方法综述
王 莉,李晓娟,2,关 永,3,王 瑞,4,王佳岳
1(首都师范大学 信息工程学院,北京 100048)
2(首都师范大学 高可靠嵌入式系统技术北京市工程研究中心,北京 100048)
3(首都师范大学 北京成像理论与技术高精尖创新中心,北京 100048)
4(首都师范大学 轻型工业机器人与安全验证北京市重点实验室,北京 100048)
E-mail:lixj@cnu.edu.cn
1 引 言
神经网络是模仿大脑神经元之间的相互作用组成的数学模型,在90年代末受当时计算机水平的限制,神经网络由于完成不了大量神经元之间的计算而陷入低潮.于20年代初,因为并行计算与GPU的发展,计算机的计算能力、运行速度得到明显提升,使得神经网络的研究与应用再次被人们推入高潮.同时,由于神经网络在人工智能方面的大规模应用,使其被广泛部署于航天器控制[1]、驾驶环境预测与自动驾驶[2-4]、机器人控制[5,6]、医学图像分析[7,8]等方面的软硬件系统中[9],而这些领域中一点微小的误差都可能会带来无法估量的损失,所以要求神经网络具有非常高的可信性.之前学术界关于神经网络可信性方面的研究主要是围绕优化训练过程以达到提高结果准确性的目的,但是随着人工智能的快速发展,对于应用其中的神经网络的可信性要求更严格,仅通过神经网络的准确性这点已经不能充分保证其可信性.
由于可信性要求的提高,同之前的计算系统相比神经网络的可信性研究需要扩展到可靠性、安全性、可用性之外,还包括不确定性、鲁棒性和可解释性等属性[10].在此基础上人们提出通过一些方法去对网络进行验证,目前关于神经网络可信性验证方法大致可分为以下类别:基于搜索的方法[11-14]、约束求解[15-19]、过度近似[20-22]和全局优化[23,24],还有一些是综合上述方法展开验证.本文通过神经网络的研究现状进行分析,在描述神经网络可信性问题相关的属性前提下,对利用形式化方法验证基于反例、抽象解释、可满足性求解、输入/输出可达性分析等可信性问题的核心算法进行分类,最后对形式化方法验证神经网络可信性的发展趋势进行总结与展望.
2 神经网络可信性相关属性
神经网络可信性[25-27]的最终要求是在输入集的基础上得到最终符合预期的输出结果,经过神经网络多次循环传播得到的预期输出概率结果,间接反应出网络的准确性,但神经网络的输出往往是难以预料的,因此仅通过网络传播过程准确率的改善并不能充分说明该神经网络可信.随着安全问题研究的深入,关于神经网络可信性验证的问题已经转变成了验证该神经网络一系列属性是否成立,分析神经网络可信性的相关属性如下:
可用性:神经网络能否完成预期操作以及是否能成功运行出输出结果;
可靠性:神经网络能否根据应用部署的要求从而对数据进行正确的操作处理;
安全性:神经网络面对攻击时能否产生结果或对于结果的准确性影响如何;
不确定性(可达性):由于神经网络的“黑盒状态”,使得其输出存在不确定性,在该情况下应用神经网络能否保证输出满足预期要求或到达预期状态.
鲁棒性:对神经网络进行有限范围干扰时,该区间内网络依旧能够保持输出和干扰前相同或能保证一定概率下相同;
区间属性:不实际运行神经网络的情况下,对应网络抽象出的模型与实际网络之间的关系;
可解释性:神经网络输出的结果能否用人类能够理解的语言方法合理的进行解释.
通过对神经网络可信性问题的相关属性进行说明后,本文将综述一些使用形式化方法[28]验证神经网络可信性问题的核心算法,如图1 形式化方法验证示意图.该方法的优势在于避免了神经网络对于每个输入值的测试,进而提供一种可证明的保证方式以防止过大或无限状态下网络不可实现的情况,如给定一个神经网络和一个属性,对其可信性形式化验证过程定义为检查该属性是否适用于该神经网络或者基于一定的数学逻辑推导出该网络在此属性下最后输出是否处于安全状态.
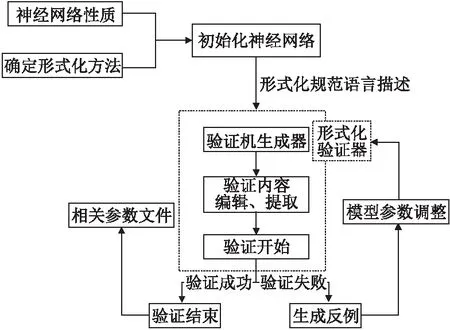
图1 形式化方法验证示意图Fig.1 Schematic diagram of the formal method validation
保证神经网络的可信性可以通过循环训练调整参数提高准确性、对网络进行验证来实现,其中验证方法是验证的关键,因此本文在神经网络可信性的一系列属性基础上抽象出可信性验证问题并概括近年来解决可信性问题的形式化方法分类以及各类方法核心算法的阐述.
3 神经网络可信性问题抽象
由于神经网络训练过程的“黑盒子”问题,使得循环训练次数再多也依旧存在不可预知的威胁,在此情况下,本文抽象出可信性验证问题并进行概括分类为以下4种:
·基于反例验证:实际运行中,神经网络输入时可能会因为受到外界的攻击导致输出同预期输出出现差异从而产生反例.而对于神经网络来说极小的扰动都可能会导致训练结果的不准确,此情况下神经网络的验证往往会部署新的逼近待验证网络再通过一致性比较来验证网络在攻击下的安全性以及鲁棒性.
·抽象解释:神经网络的训练过程为给定网络输入集,根据相应的计算规则在实际运行之后不断调整输出与预期输出之间的差距,训练过程中数据集过大或神经网络过于复杂时会出现运行时间长、电脑负荷大等问题.在此基础上提出了通过对神经网络模型抽象来将复杂的问题简单化再解决的方法,同时由于其主要是对网络抽象出的模型进行验证所以其重点是研究区间属性下的神经网络可信性验证问题;
·可满足性求解:神经网络反向传播后最后的输出只能反映训练该网络之后的准确性概率,并没有说明该网络的运行条件是否满足或者是否存在一组参数可以使得网络的属性成立从而确定神经网络的可信性;
·输入/输出可达性分析:在神经网络输入范围已知的情况下,即使中间为黑盒子,通过对神经网络进行形式化验证就可以根据网络的输入范围利用一定的数学规则对网络的状态进行可达性分析,检查网络在给定的输入范围里输出是否在安全的区间里从而验证神经网络在不确定性问题下的可信性;
依据神经网络可信性对应的相关属性归纳可信性问题,并在这4类问题基础上,对验证神经网络可信性的形式化方法的核心算法进行分类分析.
4 神经网络可信性形式化方法分类
4.1 等价性验证
神经网络的输入集在受到扰动时可能会导致网络的输出结果产生错误的分类,即使只是加入了很小的噪声干扰,但是两次网络识别出的结果可能完全不同.输入干扰导致的错误分类也会成为网络的安全隐患这一问题引起人们关注,进一步研究对抗样本[29]下神经网络安全性以及鲁棒性的可信性验证问题具有重要意义.
对于神经网络对抗性问题的验证,首先是对抗性样本的生成,如将FGSM[30,31]应用于MNIST数据集攻击后进一步生成对抗性样本.其次选取合适的方法进行验证,即神经网络受到攻击时对网络进行验证一般通过形式化方法中的等价性验证来实现,该方法主要是验证系统在受到干扰后对应的输出是否同未干扰时输出相同,基本原理是在两个系统之间根据相应的数学规则、定理等对系统进行描述,再用形式化的方法将两个系统进行一致性比较,神经网络中等价性验证的实现主要使用符号法即先将问题形式化为特定符号描述再通过相应的求解方法如求解器、定理证明器等对一致性问题求解.Yu Li等人[32]提出了一种新的针对神经网络系统故障注入攻击的DeepDyve动态验证技术.该技术与之前验证技术不同之处在于DeepDyve是为了查找网络中输出同预期输出相同的数据而不是查找反例,其新部署一个逼近要验证的原神经网络的小型网络之后通过检查小型网络产生的输出是否具有一致性,在出现不一致的输出时则对原神经网络进行调整来使网络具有可信性.该方法核心在于比较对抗性样本下神经网络能否产生正确的输出,主要对网络的可用性,安全性以及鲁棒性等可信性属性进行验证,而不是依据输入产生预计输出验证神经网络的可靠性、不确定性或者可解释性等属性.
4.2 抽象解释验证
4.2.1 基于抽象的过度逼近
在现有的使用形式化验证神经网络的可信性方法中,模型检测有数据量过大时导致状态空间爆炸的问题,而定理证明由于是基于数学逻辑展开使得对于操作者的数学功底与逻辑思维要求比较高,这些常导致形式化验证方法在实际的应用中受到局限.在这种情况下,采用抽象解释的方法对神经网络进行可信性验证,由于其不需要实际的运行网络使得该方法可以有效的避免以上局限性的问题,该方法主要思想是在可信性验证过程中将复杂的问题近似抽象以后通过分析其核心组成达到降低复杂度的目的,在神经网络可信性验证中抽象解释一般在输入集区间内用抽象域去近似网络的输入,具体操作为在神经网络的输入层上定义具体的域,输入集合包含于该域,此时为了计算的效率选择一个比较简单的域作为抽象域,其可以过度逼近输入层具体域中变量的范围与关系,所以对于抽象域的选择很关键,对验证的效率与准确性有决定性作用,在形式上,一个抽象域由表示为一组逻辑约束.
基于过逼近的抽象方法是通过对神经网络或对其输入集进行过度近似后在区间属性下对网络的可信性进行验证.Timon Gehr等人[20]提出了使用AI2,基于过度逼近的方法引入抽象转换器来获得网络的行为从而自动证明神经网络的安全属性.在实际应用中,神经网络在输入时时常会遇到干扰使得网络对分类产生错误的判断,而实践证明输入扰动能产生对抗性例子,AI从选取的抽象域中提取元素过度逼近输入集合,根据抽象转换器返回的结果来验证属性,AI2需要分析神经网络运算过程中每层神经元产生的所有可能输出,通过神经网络编码成逻辑公式之后再用约束求解器来验证网络的鲁棒性,论文还针对选用不同的抽象域来说明抽象域对于使用AI2验证神经网络鲁棒性的影响.Yizhak Yisrael Elboher等人[33]提出抽象一个过度逼近原待验证网络的小型网络,并对该小型网络进行规范验证,如果待验证属性在小型网络满足则该属性也可以适用于原网络,反之则提供一个反例,并使用该反例去反向调整网络从而提高网络的正确性.S.Gokulanathan等人[34]通过简化神经网络来对其进行验证.Ravi Mangal[35]等人提出了概率鲁棒性的概念,通过抽象解释去近似网络的行为从而对神经网络中不满足鲁棒性的输入集合过度逼近,使用重要性抽样的方法来对其进行对抗得到神经网络违反鲁棒性概率的准确估计.该方法关键技术是对神经网络进行一个抽象简化之后进行可信性验证,因此对于抽象出来的网络具有完整的结构是网络可信性相关属性可以得到验证的关键.
除了对网络抽象[36]还可以对网络的状态进行抽象来实现可信性的验证,如通过后继状态进一步来反向推断安全情况下神经网络的输入状态.Xiaowu Sun等人[37]介绍了一种具有神经网络的自助机器人,通过构造系统终止状态的抽象,并通过其可达性分析来计算安全的初始状态集合,使得该机器人从安全的初始状态出发保证其在具有多个障碍的空间里可以安全躲过障碍.基于有限状态抽象,该方法能够验证网络的可用性、可靠性与区间属性等可信性属性,但是神经网络的安全性、不确定性以及鲁棒性等属性的可信性验证还有待进一步研究实现.
4.2.2 基于定理证明验证
形式化过程是开发一组通用的数学模型和定义的过程,其中定理证明[38]是基于演绎推理的广泛用于物理系统验证的形式化方法技术.通过定理证明的方法对神经网络的可信性进行验证,先建立网络对应的数学模型,再利用推理验证其预期的性质,是根据已有的公理或者已经被证明出来的定理添加推理规则直到推出所要验证的定理的过程,如验证神经网络可信性属性中的可解释性,可以通过自然语言或者逻辑规则建立网络相应的数学模型,再用人类所能理解公理或定理进行解释.
在网络可信性验证中,对于底层逻辑的判定问题,定理证明器可以自动或交互式地完成,由于命题逻辑是可判定的,因此在该逻辑中表达的句子可以使用计算机程序自动验证,而高阶逻辑是不可判定的,因此用高阶逻辑表示的句子定理必须以交互式的方式然后用户提供指导来验证.Adnan Rashid等人[39]通过在HOL4定理证明器中形式化了z语法,开发了一个形式化推理分子反应的演绎框架,并且在高阶逻辑中形式化了z语法的逻辑运算符和推理规则.Abdorrahim Bahrami等人[40]通过Coq定理证明器验证了一些基本神经元结构的动态行为性质,提出并证明了4个重要属性,从单个神经元的属性与输入和输出之间的关系开始,转向更复杂的属性,从而提高整体神经网络的可信性.Coq实现了一个具有高度表达力的高阶逻辑,通过直接引入神经元结构的建模数据类型,表达它们的属性,也由于Coq在证明过程中具有通用性,使其可以证明任意参数值的属性,如任何时间长度,输入序列,或任意数量的神经元等.定理证明主要用于验证网络的可解释性,网络可解释性基于网络的可用性之上,通过一定的逻辑规则推理出网络的输出结果对网络的可靠性、不确定性以及区间属性进行可信性验证.
通过基于抽象的过度逼近以及定理证明来解决神经网络可信性问题中的抽象问题,使得复杂的或者难以实现的可信性问题通过抽象简化逐步实现验证的目的.
4.3 基于模型检测验证
模型检测[41,42]是通过对系统构造出的模型状态空间的遍历来确定系统属性的准确性从而判断系统是不是符合设计需求.在形式验证中,通常基于如图2所示的转换图原型来定义神经网络的模型[43].对于神经网络的可信性验证,模型检测在有限状态下对网络穷举搜索,验证依赖属性的可满足问题,在结果为真的情况下则表明网络是符合性质的,反之则不符合并且会相应的给出一个反例[45],而且在网络可靠的情况下根据对神经网络状态是否可达预期状态,模型检测的方法可以验证在不确定性时对应的输入/输出范围问题下神经网络的可信性.因此,模型检测方法验证网络可信性的核心算法可以分为属性可满足性问题与状态可达性问题.

图2 神经元状态转换图原型[44]Fig.2 Prototype neuronal state transition diagram[44]
4.3.1 可满足性求解
神经网络可信性验证中可满足问题进行分析后可以通过形式化方法中的模型检测来解决,由于可满足问题主要是验证属性在神经网络中是否得到满足,可以将验证问题转化为一组约束再通过相应的约束求解器进行求解的过程.可信性属性中的可用性和可靠性,便可以将其定义编码成相应的条件约束,再选择合适的求解器进行求解,如果结果为真,说明至少存在一组参数使得该网络属性成立,验证出网络的可用/可靠性.研发成熟的求解器可以解决较大规模的实际问题,先后出现了各类求解器可给出能否有满足相关约束问题的解,如SAT求解器、LP求解器、MILP求解器、SMT求解器等,求解器工作过程如图3.将需要解决的实际问题建模为约束可满足问题,其中关于使用该思想对神经网络进行验证也一直是研究的热点,近年通过可满足问题进行网络可信性验证方法如下:

图3 求解器工作过程图Fig.3 Working process diagram of the solver
A.基于SAT和线性规划组合方法
给定一组实值变量上的线性不等式和一个线性优化函数(它们一起被称为线性规划),对应的线性规划问题是利用求解器找到对满足所有约束的最小化目标函数变量的赋值,通过求解出满足约束的值使得网络在部署过程中满足可信性.Ruediger Ehlers[46]提出了针对用分段线性激活函数的前馈神经网络的验证方法.基于SAT与线性规划组合将神经网络线性近似,该近似可以添加到神经网络验证问题的SMT或MILP实例编码中,可以在验证过程中排除未激活神经元的大规模搜索,不仅将近似作为求解器的条件约束,还通过弹性滤波算法在发生冲突时寻找最小不可行线性约束集,使其与推测隐藏节点相位过程结合从而选择安全的节点相位,对节点相位进行单元传播类推理,用于神经网络中的节点选择.Hemali Angne等人[47]研究模拟图神经网络来解决NP-complete问题,通过SAT公式将图神经网络可视化来描述相应的属性.
B.可满足性模理论的方法
用可满足性模理论的方法验证神经网络的过程是将网络抽象为一组线性算法约束的布尔组合,证明当抽象模型是安全的时,具体的网络则是安全的,当模型不安全时则会提供相应的反例来进行网络的改进.首先将网络的约束转换为布尔约束,再检查相应的算数理论中分配的一致性,当存在满足神经网络中所有约束的分配则说明网络是可满足的,即先给定网络输入的先决条件保证其满足规定去输出后置条件.
Luca Pulina等人[48]提出的验证方法考虑了检查神经网络3种安全条件即网络的输出是不是在规定的安全区间、网络的输出是不是逼近局部的预期输出、在输入集出现微弱攻击变化时输出会不会受到影响,将检查的条件编码为线性算法的约束可满足性问题,通过可满足性问题对网络进行可信性验证.
在可满足性模理论方法里,SMT求解器的应用最为广泛,同时SMT在线性逻辑约束优化问题中也是解决问题的关键,利用SMT求解器找到满足符合问题的约束条件和优化目标抽象出来的目标函数和约束表达式的解的集合,再从集合里找到使得目标函数取得最值的解为最优解.Guy Katz等人[49]提出一种高效的SMT求解器Reluplex,其中神经网络可以抽象为线性组合,为了提高其性能给其增加了激活函数使其转为非线性,但是非线性给神经网络的验证增加了不确定性,为了解决这个问题提出了将Reluplex用在ReLU激活函数的可满足约束求解上.即在给定的输入输出情况下,设置两个变量分别用于单个的ReLU节点去连接前后一层的节点,根据ReLU函数自身的取值以及输入输出值定义约束条件之后,使用求解器求解是否有满足这些条件对应的变量值,从而对神经网络进行验证.Clark Barrett等人[50]提出基于单纯形方法通过处理ReLU约束来进一步对神经网络可信性问题进行验证,通过在Reluplex基础上将相关属性编码成其输入约束进行属性可满足性验证.Luca Pulina等人[51]提出通过SMT求解器编码解决验证MLPs的输出包含于具体的一个安全的区域里并且验证其逼近具体的值或在区域内调整目标的误差方差.Xiaowei Huang等人[13]在SMT的基础上提出了一种对于前馈神经网络分类决策进行自动验证的框架,使用离散化的方法进行有限的穷举搜索从而保证错误分类被找到,进一步将验证问题转化为对反例的搜索问题.
C.基于MILP方法
对神经网络编码过程中,将对应的约束添加到MILP求解器中,根据求解的结果判断网络是否处于预测状态来对网络的可信性进行验证.在给定的神经网络与输入集合时,为网络的输出预测一个范围并且可以保证所有的输出均为该范围内的子集,通过非线性激活函数的分段线性化来定义神经网络语义到混合整数约束的编码,将输入约束添加到MILP中使得输出变量分别实现最大化和最小化来推断安全范围,同时MILP查询比较是否存在比局部极小值更优的解来对局部最优进行选择,从而达到利用神经网络的局部特性同时又解决了局部最小值的目的.Souradeep Dutta等人[52]提出一种有效的范围估计算法,它在使用混合整数线性规划问题的全局组合搜索和重复寻找由神经网络表示的函数的局部最优的局部优化之间迭代,通过修剪次优节点,有效地减少了神经网络中活动神经元可能的组合搜索.Michael E.Akintunde等人[53]提出了一种基于MILP的代理-环境系统的验证,其中代理是通过前馈神经网络实现的,环境是不确定的.关于该类系统对CTL属性的验证问题,假设神经网络与非确定性环境交互,其中环境状态的非确定性使神经网络不能完全控制更新和观察环境状态,基于该假设下的系统演化不是线性的,而是针对分支时间时序逻辑研究这类系统的验证问题,即通过将系统在有限的执行步骤中神经网络应该产生的状态编码到MILP中进行求解,验证系统在有限步骤的执行下是否一直在安全状态范围里.Matteo Fischetti等人[54]研究了将神经网络建模为0-1的MILP并将对应的输出同ReLU结合通过二进制的变量研究网络的性质.Ansgar Rössig等人[55]将MILP与逼近技术结合提出了一种验证神经网络输入没有独立边界的实例问题的求解器,建立比较线性逼近理论框架去处理ReLU对应神经网络的线性松弛问题.
针对属性可满足问题的神经网络进行可信性验证主要在于编码时添加的约束,不管使用的是基于哪一种求解器的算法其核心都是对约束条件进行一个求解的过程,只要添加的约束符合所要验证的属性,那对应求解出来的结果就是对神经网络可信性的说明.
4.3.2 状态可达性研究
状态可达性是神经网络在初始状态经过一个或多个操作之后下一个状态是否达到的是预期状态的问题,其对应的就是在神经网络输入/输出范围问题的基础上根据一定的规则推断出网络的状态从而将神经网络可信性问题转换成网络的可达性问题进行研究,将可达性问题用于神经网络的可信性验证的研究主要有两种:
A.通过神经网络函数值上下界之间值的可达性来验证网络在不确定性下的可信性.
给定一个神经网络,用一个函数来计算输入集与输出函数值的上下界,假设给定条件该函数为 Lipschitz连续函数时该函数是通用的即上下界区间内的所有值都是可达的,在证明了前馈神经网络函数是 Lipschitz连续时再进一步证明了安全验证问题可以转化为可达性求解问题,从而根据全局的最大值与最小值来对可达性问题求解来达到验证网络可信性的目的.Wenjie Ruan等人[23]通过实例化可达性问题来对神经网络进行安全验证、输出范围分析,并且针对可达性问题,提出了一种基于自适应嵌套优化的新算法对网络的可信性进行验证.
B.通过对神经网络输出集的可达性与输出范围结合分析来验证网络在不确定性下的的可信性.
神经网络被看成一个黑盒时,对给定输入产生所需要的输出时可能由于各种原因会导致不安全输出,因此研究一个可能覆盖所有神经网络输出值的输出可达集来对网络进行安全分析,对网络的可信性验证来说十分重要,验证示意图如图4所示.Weiming Xiang[56]等人通过计算神经网络的输出损失对于输入与权重之间的数学期望来表示有界输入下输出的最大偏差,称其为最大灵敏度,通过输入空间的离散化来实现对输入集的穷举搜索,组合模拟产生的每层灵敏度以获得输出可达集的估计,将神经网络的输出可达集估计问题公式化为一系列优化问题,最后通过检查估计的可达集和不安全区域之间的交集来对网络进行安全验证.S.Dutta等人[14]提出了一种基于MILP的算法专门用来对使用ReLU作为激活函数的神经网络进行输出范围分析.Shiqi Wang等人[57]提出了通过符号区间算法来根据神经网络的输入范围去估计网络的输出范围,即给定网络的输入范围以及安全属性,通过ReluVal按照神经网络传播的方向计算出对应的输出范围,同时设计误差估计优化算法提高输出范围的准确率,如果在估计的输出范围里能够满足网络的属性则表明网络的属性得到验证,反之则在区间中抽取输入检查不安全情况,当检查到有与网络属性不符输入的情况时,将其作为反例输出.Guoqing Yang等人[58]在ReLU为激活函数的神经网络中使用 SHERLOCK验证工具对神经网络的输出集进行估计从而验证神经网络的可信性.Chih-Hong Cheng等人[59]提出了一种基于假设保证的神经网络验证方法,通过学习一个输入属性特征描述器,使得输入满足一定的约束前提时,神经网络的输出不会出现预期以外的情况,通过把输入集的特征聚合到神经网络的输出中,再通过询问输入特征网络是否可以输出为true来解决安全验证问题从而直接对感知神经网络的安全性进行验证.
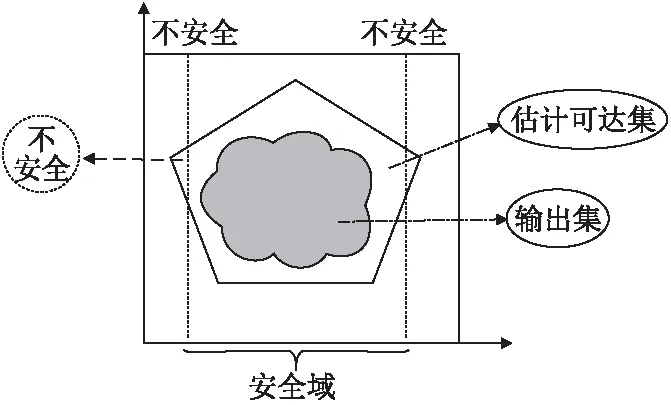
图4 输出可达验证示意图Fig.4 Output up to validation diagram
综上对于关注输入/输出范围问题下神经网络由于黑盒导致不确定性的神经网络可信性验证可以通过保证在初始状态下部署的每一个状态都能到达安全状态来验证,或者可以通过在输入/输出范围下来对网络的输出集进行一个估计,使得网络的输出包含于该估计,同时该估计与不安全状态不产生交集从而验证网络的可信性,也由于该方法是基于区间范围,其对于神将网络的可用性、可靠性以及不确定性的验证比较有效,而关于网络的安全性、鲁棒性等属性的验证具有一定局限性.
4.4 总 结
根据上述讨论,在表1中分类总结了现有验证神经网络可信性的形式化方法,并结合对应的基于反例验证、抽象解释、可满足性求解、输入/输出可达性4类不同的问题对网络满足的属性验证的情况进行分析.
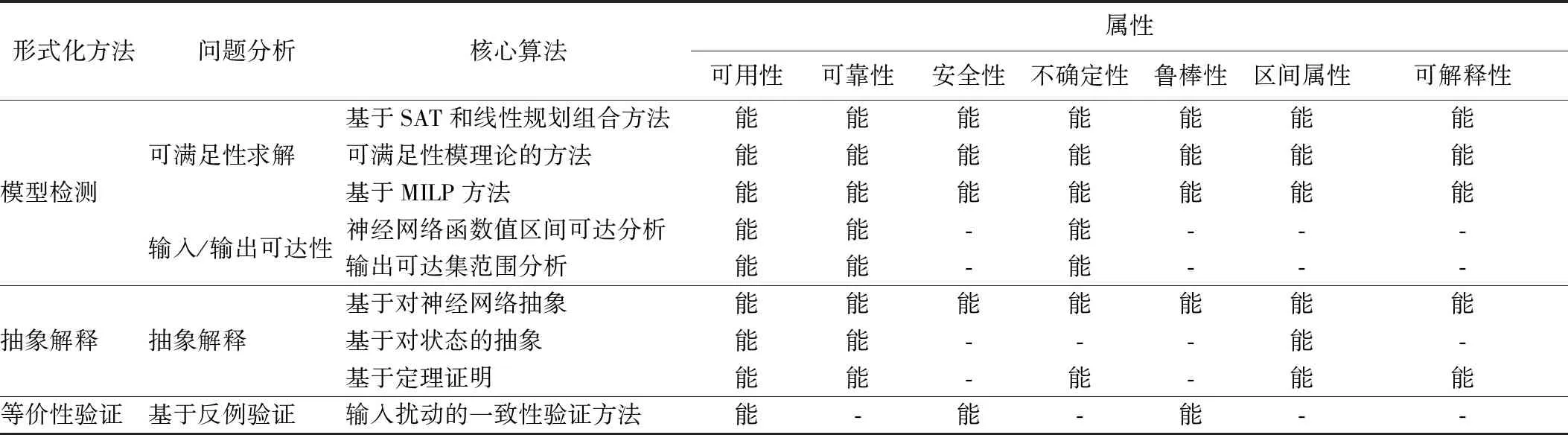
表1 神经网络验证方法归纳说明Table 1 Summary of the neural network validation method
5 发展趋势展望
神经网络在各类应用上部署的广泛性使其发展取得了可观的成效,在人工智能领域作用越来越大,因此其安全方面的可信性研究逐渐成为人们关注的重点,研究的深入使得许多问题也逐渐暴露出来,因此,关于未来的研究可以考虑以下几个方面:
1)鲁棒性
神经网络的输出结果受输入集影响很大,即使是微小的扰动对于网络的输出来说可能会得到一个完全颠覆的结果,因此,神经网络鲁棒性的研究对于网络可信性验证至关重要,在一定的程度内保证神经网络具有容错性,使得输出受干扰的影响尽可能降低,网络的安全可信性得到保证.
2)定量验证
随着研究的深入,单纯的定性分析已经不能够满足安全性的说明,近期有人引入定量验证的方法来对神经网络安全性进行验证,如Teodora Baluta等人[60]提出了对神经网络的定量验证,从验证神经网络是否违反了属性转变成有多少输入能够满足属性.提供了一个新的分析框架将神经网络与属性的给定集合建模为逻辑约束集合,使得量化神经网络满足属性的数量问题简化为对属性的模型计数问题,以定量的形式对神经网络属性进行满足性验证.随着定量分析概念的提出,关于该方法的研究也引起人们的关注,Du Xiaoning等人[61]基于递归神经网络,提出了一个定量分析框架(DeepStellar)用于在输入出现扰动时进行安全分析,在其基础上开发对抗样本监测器,检测对抗攻击从而保证神经网络的可信性.近年来神经网络验证主要在于定性上面,定量分析验证的提出为网络可信性验证提供了一种新且有效的研究思路,值得人们进入更深层次的研究.
3)特征提取[62]的准确性
神经网络可信性验证属性中输入集的处理至关重要,而神经网络最初在处理输入集的时候是一个特征提取过程,可以说特征的提取直接关系到网络可信性验证结果.例如,图像识别一只猫,连初始提取猫的特征都不正确,最后不可能得到正确的识别结果,并且目前关于人工智能的应用部署里大部分都是基于特征提取而展开工作,因此,特征提取的准确性是最后可信性验证的先决条件,也是需要考虑的关键之处.
4)可信性形式化验证方法的拓展
随着研究的深入,神经网络的训练不足以体现网络的安全性,近几年使用形式化方法对网络可信性验证处于快速发展阶段,许多现有的方法还具有各自的局限性,所以,对于验证方法的完善以及提出创新性的方法和工具依旧是需要关注的重点之一.
5)神经网络可信性验证规范和验证技术的发展
神经网络在各类人工智能项目中的广泛应用使得对其可信性要求越来越高,也因此形式化方法验证神经网络可信性的研究成为热潮,同时验证规范与验证技术要求会随着发展逐渐严格,值得人们进行更深入的研究.
6 结 语
由于对神经网络可信性要求的提高,关于其可信性验证成为近年来的研究热点,除了早期的循环训练改善网络以外,本文分类综述了神经网络可信性研究的一系列属性、可信性问题的抽象表达,并通过形式化的方法对神经网络可信性验证的研究现状,对基于反例验证、抽象解释、可满足性求解、输入/输出可达性分析等问题验证过程的核心算法进行阐述,最后提出目前发展的瓶颈、需考虑的问题以及未来的发展趋势.

