霍曼转移结构光束设计及微粒操纵(特邀)
李新忠,朱刘昊,樊海豪,魏文军,马鑫,秦雪云,胡华杰,台玉萍
(河南科技大学物理工程学院,河南洛阳 471023)
0 引言
霍曼转移是1925 年德国工程师WALTER Hohmann 博士推导出在两条倾角相同、高度相异的圆形轨道间转移卫星的最小能量方法[1],在航天领域应用非常广泛[2-3]。但其实微观世界中也存在有轨道运动,且微观运动是否可以适用霍曼转移尚未经过探索。光镊作为一种无接触、无伤害的微操纵工具已经广泛应用于微操纵领域,在细胞生物学[4-9]、材料组装[10]、光物质相互作用物理和化学[11-12]等领域发挥着重要的作用。
1992 年ALLEN L 发现了轨道角动量[13],这就直接赋予了光镊一个横向的扳手力。这个扳手力的来源就是光子绕着光轴旋转所产生的轨道角动量。在对轨道角动量的研究中已经产生了许多应用,如2004 年KOSTA Ladavac 就提出使用光涡旋阵列组装和驱动光机械泵[14],2012 年WU Tao 提出光子驱动的微电机可以诱导神经纤维生长[15],2015 年YAN Zijie 利用光镊的相位梯度制备银纳米粒子的材料组装[16],2020 年,RODRIGO J A 通过定制光学推进力用于控制共振金纳米粒子和相关的热对流流体的传输[17],之后2021 年他又提出使用全光控制金属纳米粒子,并可以自由的定制三维轨迹[18]。但不论光的结构被如何改变,由于轨道角动量的性质,其结构光束在具体的应用中都会使粒子始终沿着一个既定的轨道进行运动。而粒子的实时变轨运动则没有被考虑。因此目前亟需一种与以往的单一轨道角动量相比具有更加丰富的模式可以同时存在多种不同轨道角动量并实时调控粒子运动轨道的光束。
为了打破这一现状,本文通过研究霍曼转移的原理,并通过结合光束塑形技术、坐标变换技术、傅里叶相移定理将其融合到结构光场中,提出了一种霍曼转移结构光束。该光束具有非常丰富的调控方式,并且其相位梯度分布可以使粒子从停泊轨道转移至同步轨道。之后通过调整参数成功生成了复杂霍曼转移结构光束,可使粒子进行多次变轨运动。最后搭建了实验光路并使用聚苯乙烯进行了光镊实验,实验结果与理论相符,证明了其可行性。该研究成功的将霍曼转移应用至微操纵领域,对光镊的发展具有重要意义。
1 霍曼转移轨道及其结构光产生原理及调控
1.1 霍曼转移轨道及其结构光产生
要想在光场中生成对应于霍曼转移轨道原理的结构光束,首先需要剖析霍曼转移轨道的原理。如图1(a)所示,霍曼转移轨道由三个子轨道组成,分别是黄色的停泊轨道Q1,绿色的转移轨道Q2,蓝色的同步轨道Q3,其中停泊轨道Q1 和同步轨道Q3 为圆形轨道,转移轨道Q2 为椭圆形轨道,且r1,r3分别是轨道Q1和轨道Q3 的半径,r2是轨道Q2 的半长轴。它们之间的关系满足r3=nr1,r2=(r3+r1)/2,其中n为该停泊轨道和同步轨道的比值,图1(a)中n=3。图中Q1 和Q3 都是圆形,光强相同,而Q2 是一个椭圆,光强相对较弱。这是由于在对圆形变成椭圆的过程中结合了坐标拉伸技术,所以Q2 的光强相比于Q1 和Q3 较弱。需要注意的是,停泊轨道Q1 和同步轨道Q3 的圆心是重合的,但转移轨道Q2 的圆心与他们二者并不重合,两个圆心之间的间距为r1。并且,转移轨道Q2 的椭圆率e是一个自由参数,可以根据实际需要进行调整,比如当需要绕过特定的障碍物时。

图1 霍曼转移轨道Fig.1 Hohmann transfer orbit
若要在光场中相应的实现以上功能,需要使用光束塑形技术。但目前存在的大多结构光塑形技术非常依赖于参数方程[19-20],只能产生已经明确具有参数方程的形状。但霍曼转移轨道并不存在相应的参数方程,因此无法直接实现。因此在普通的光束塑形基础上需要结合其他技术得到可以实现霍曼转移轨道的结构光束。
首先简单介绍一下本文中所使用到的塑形技术[21],该光束的表达式为

式中,(ξ,η)是傅里叶变换后的坐标系,Hi(x,y)是计算全息图的透过率函数,可以表示为
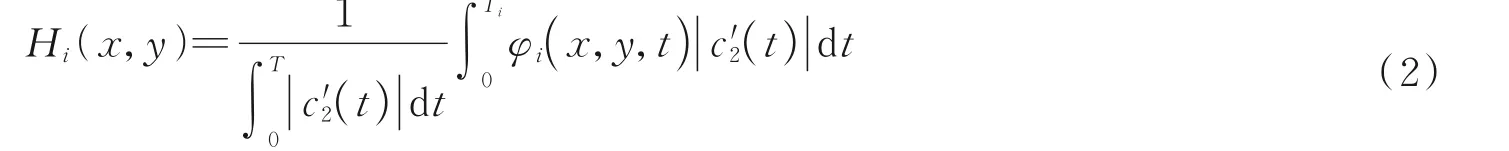
式中,|c'2(t)|=[x'0(t)2+y'0(t)2]1/2,t∈[0,Ti],x0(t)和y0(t)是曲线的参数方程,决定着曲线的形状,φi(x,y,t)是相位项,具体可以表示为
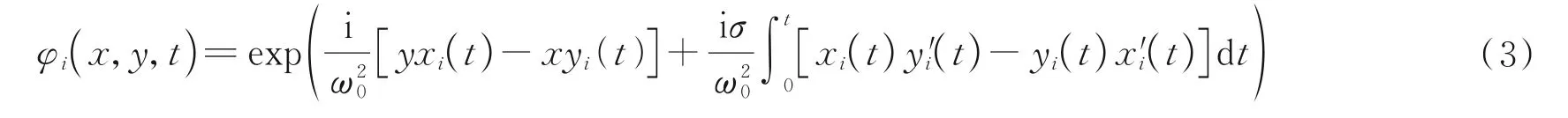
σ是一个用来控制沿着曲线相位梯度也即拓扑荷值的自由参数。ω0是光束的束腰宽度。为了得到霍曼转移轨道,首先需要单独的生成三个轨道。由于停泊轨道Q1 和同步轨道Q3 是圆心重合,半径不同的两个圆,因此它们参数方程分别为
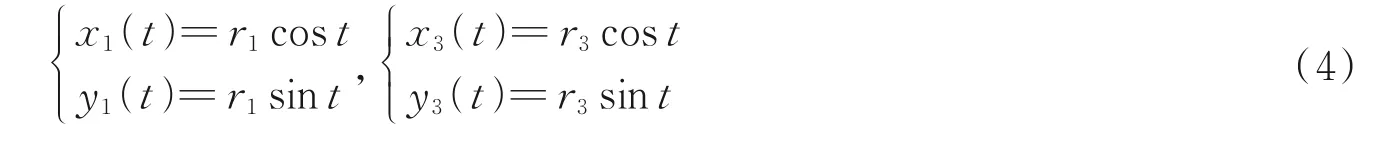
若此时Ti=2π,则可以组成两个空心圆环。但在霍曼转移轨道中所需要的是两个半圆环。因此此处需要使Ti=π,将式(4)代入式(2)即可得到生成停泊轨道Q1 和同步轨道Q3 所需要的全息图透过率函数H1(x,y)和H3(x,y),之后再带入式(1)即可得到该光束的复振幅E1(ξ,η),E3(ξ,η)。不同的是,转移轨道Q2是一个椭圆轨道,而且圆心与停泊轨道和同步轨道并不重合,因此这里需要使用坐标变换技术和傅里叶相移定理[22-23],所以其参数方程可以使用圆形的参数方程,即x2=r2cost,y2=r2sint,之后在带入式(2)的过程中,对其坐标系进行拉伸处理,其坐标系变为x0=x,y0=αy,其中α为拉伸系数,它与离心率e之间的关系为e=sqrt(1-α2),之后得到其全息图透过率函数H2(x0,y0)。最后再代入式(1)对其进行相移处理,并得到其光束的表达式为
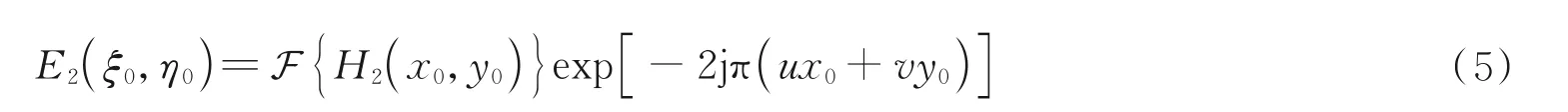
式中,ξ0=ξ-u,η0=η-v,u,v是偏移量。此时偏移量等于r1,之后将三者相加即可得到霍曼转移结构光束的计算全息图透过率函数Htotal(x,y)和Etotal(ξ,η)。至此已经完成了对霍曼转移结构光束的理论描述,之后选用r1=0.3 mm,拓扑荷值分别为m1=20,m2=20,m3=40 对光束进行模拟产生。其光强Itotal=|Etotal(ξ,η)|2如图1(b)所示,其相位如图1(c)所示,从图1 中可以明显的观察到光束分为Q1、Q2、Q3 三个轨道,其相位梯度沿着轨道均匀分布。
1.2 霍曼转移结构光束的调控
依据霍曼转移轨道建立的霍曼转移结构光束,通过适当的调控,可以令其具有比霍曼转移轨道更加丰富的性质,首先由于霍曼转移轨道中三个子轨道的大小是互相联系的,如图2(a)所示,图中停泊轨道Q1与同步轨道Q3 的比值n=3 时,意味着不论停泊轨道大小如何,在粒子经过转移轨道后,会被转移到一个三倍于停泊轨道半径的同步轨道上。因此整个系统通过改变停泊轨道Q1 的半径就可以改变整个系统的大小,图2(a)为半径改变之后的霍曼转移结构光束的光强分布。同时,如图2(b)为相对应于图2(a)霍曼转移结构光束的相位分布,由于依托于塑形技术所得到的光束具有“完美性”,因此可以限定其半径不随拓扑荷值改变。这样在操纵粒子时就可以自由的控制粒子运动的速度,从而应对不同情景下的应用需求。

图2 不同半径停泊轨道Fig.2 Parking orbit with different radius
更进一步地,通过继续附加额外的转移轨道以达到多次变轨的需求。接下来将对复杂霍曼转移结构光束进行模拟生成及性质研究。为了更方便的观察效果,其参数设置为:停泊轨道半径r1=0.1 mm,m1=2,n=2,若设j=1,2,3,…为轨道后续依次排序的编号。则其后续所有轨道的半径需符合r2=1.5r1,r3=2r1,r4=1.5r3,r5=2r3,r6=1.5r5,r7=2r5,r8=1.5r7,r9=2r7,…,以达到变轨的目的,拓扑荷值设定服从mj=(rj/r1)m1以达到相位分布均匀的目的。以此方式生成的霍曼转移结构光束计算全息图透过率函数和光束表达式可以表示为
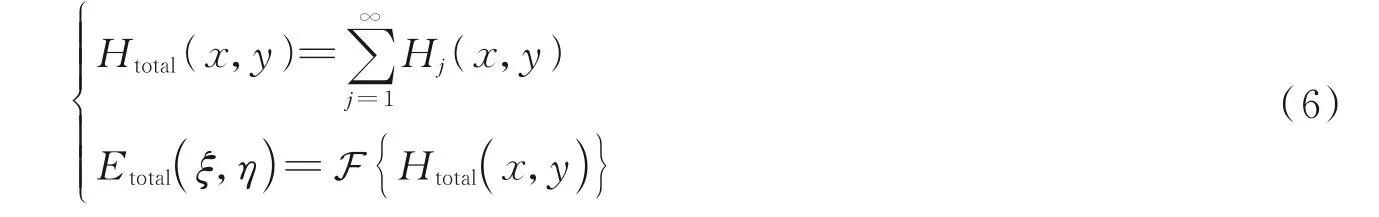
最终得到的霍曼转移结构光束的光强如图3(a)所示,每当增加一次转移轨道,上一次的同步轨道便会成为第二次的停泊轨道。以此类推即可得到复杂的霍曼转移结构光束。同时相位图如图3(b)所示,可以明显的观察到,相位呈现均匀分布,这样在微粒操纵时可以给予粒子均匀的相位梯度力。
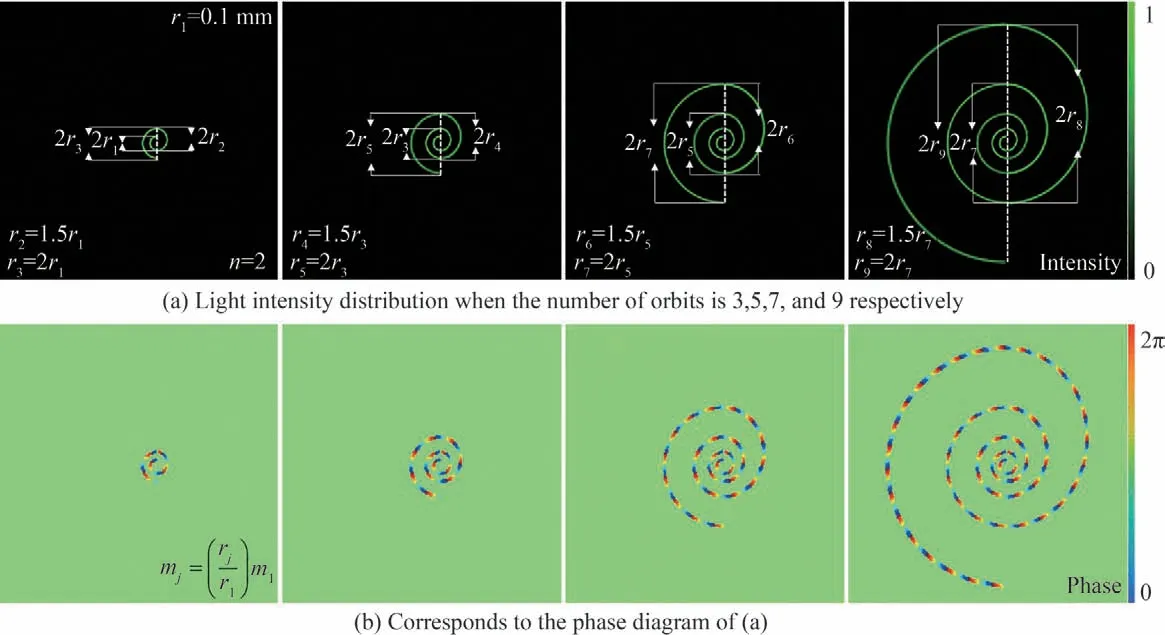
图3 不同轨道数量Fig.3 Different number of orbits
2 微粒操纵实验验证
2.1 实验装置及微粒介绍
在模拟生成相应的霍曼转移结构光束之后,需要对其在实验中生成并进行微粒操纵的验证。首先搭建一个实验光路,本文使用的光路图如图4 所示,其中激光器(532 nm,0~5 W 可调)输出的光经过透镜L1 和透镜L2 所组成的扩束系统进行扩束并调整为平行光,之后经由偏振片P1 转换为线偏振光输入到空间光调制器(SLM,HOLOEYE PLUTO-VIS-016,像素尺寸为8 μm×8 μm)上,之后经过透镜L3 和透镜L4 组成4F 滤波系统进行滤波得到SLM 衍射出来的+1 级衍射光。+1 级衍射光最后经由透镜L5 耦合进入显微物镜MO1(100×,oil,NA=1.2)中,被显微物镜聚焦至样品室的粒子上。照明光路中的LED 光(波长620±20 nm)经由显微物镜MO2(40×,NA=0.4)聚焦至样品室进行照明,之后照明光经过二向色镜(反绿光透红光)输入到CCD(BasleracA1600-60gc 型彩色相机,分辨率为1 600 pixel×1 200 pixel,像素尺寸为4.5 μm×4.5 μm)上被计算机记录下来。同时偏振片P2 可以用来去除二向色镜反射不完全的绿光。本次实验中所使用的粒子为3 μm 的聚苯乙烯粒子,溶剂为蒸馏水。图4(b)为本次实验中输入到SLM 的掩模板,其表达式为T=exp{i[angle(Etotal(ξ,η)+2πx/d]},其中angle()为相位函数,d为闪耀光栅的周期。图4(c)为本次实验中的光束,可以看到其光强分布与模拟结果基本相同。
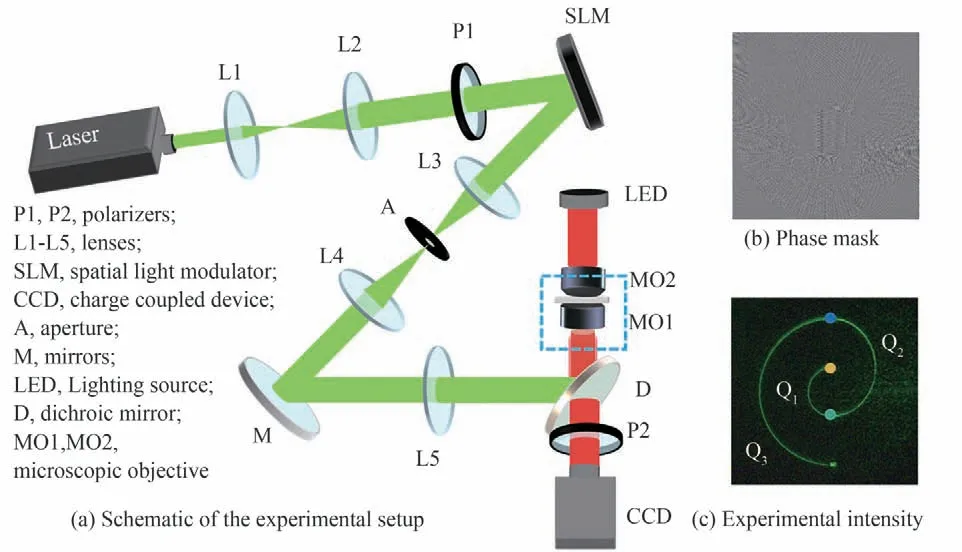
图4 实验装置及掩模板和实验光强图Fig.4 Experimental setup,phase mask and experimental intensity
2.2 实验结果与讨论
为了证明霍曼转移结构光束的优越性,设计两个实验进行验证。第一个实验使用如图4(c)中的光束照射粒子,使粒子从停泊轨道转移到同步轨道。由于实验中的光束经过一系列反射,会导致反向,因此,实验中所使用的光束参数为r1=0.3 mm,n=3,m1=-40,m2=-40,m3=-60。最终的实验结果如图5 所示,可以看到粒子沿着既定的轨道,从小的圆轨道成功转移至目标大圆轨道。该实验验证了上文的理论预测,实现了变轨运动。

图5 霍曼转移结构光束微粒操纵实验结果图Fig.5 Experimental results of Hohmann transfer structure beam particle manipulation
第二个实验使用动态切换SLM 上掩模板的方式,由于SLM 可以实时切换掩模板,因此先分别生成三个完整轨道的掩模板,即Ti全部等于2π。之后使粒子分别在停泊轨道旋转一周半之后,选择合适时机切换转移轨道掩模板,再旋转一周半之后,转移至同步轨道并在同步轨道旋转一周。以此来证明在微观世界使粒子在运动中切换轨道的可能性。最终的实验结果图6。从图中可以清楚的看到,粒子从较小的黄色轨道,之后变轨至绿色椭圆轨道,最后变轨至更大蓝色的同步轨道上。值得注意的是,三条轨道周长不相等,并且每条轨道携带的拓扑荷不相等,相位梯度不相同。并且,在轨道变换时激光器的能量是保持不变的,因此轨道上的光子分布也变得更加稀疏,最终导致粒子在三条轨道上的运动速度不同。如果需要,可以通过改变光束参数和调整激光器能量来得到稳定的匀速运动。
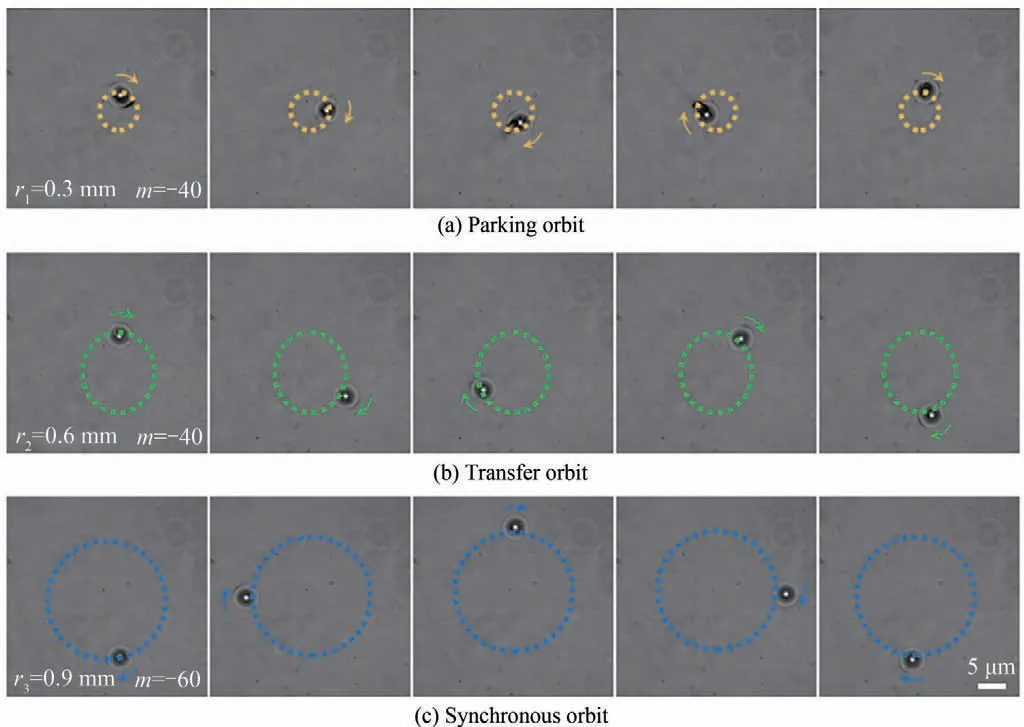
图6 SLM 动态变化掩模板使粒子变换轨道Fig.6 Particle change the orbit via SLM dynamically changes the phase mask
3 结论
结合光束塑形、坐标变换、傅里叶相移技术成功的将霍曼转移应用至结构光中,提出了一种模式丰富可调的霍曼转移结构光束。该光束的大小,相位梯度分布均可任意调制,并且理论上允许粒子从停泊轨道转移至同步轨道。最后在实验中对其进行了验证。可预见地,该光束可以通过改变拓扑荷值的正负,来反转停泊轨道和同步轨道,或者通过分别调整各个轨道的拓扑荷值来控制粒子在各个轨道之间运动的速度,或者通过整体旋转、翻转光束来控制粒子转移的方式。该研究充分证明了霍曼转移在微观世界中的可行性,在光学微操作领域具有重大意义。

