离心泵出口液控阀门的故障监测方法研究

杨 成，于永海，周永伟，封 林，闫浩迪

（1.白银市兴堡川电灌工程管理局，甘肃白银 730900；2.河海大学农业科学与工程学院，南京 210098；3.江苏航天水力设备有限公司，江苏扬州 225600）

0 引 言

离心泵是高扬程泵站常用的叶片泵类型，一般其出水管道比较长，在水泵出口需要安装液控阀门［1］。液控阀门在水泵开机和停机过程中的开启与关闭规律直接与水泵系统水锤及其防护相关联，不适当的出口阀门操作规律极易造成泵系统的水锤危害，比如爆管、水泵机组倒转转速过高，影响工程的安全稳定运行。当出水管道长度超过泵站净扬程的30 倍时在泵站设计时必须进行泵站事故停机工况的水锤计算，进而合理确定水锤防护措施［2-4］，包括泵出口阀门的关阀规律和单向调压室、气压罐［5，6］、空气阀等水锤防护设施。

随着泵站计算机监控技术日趋成熟和稳定，为泵站实现“无人值班、少人值守”运行管理模式提供了技术支撑。在此基础上可建立功能完善的远程测控系统，实时掌握运行状态信息，及时发现存在的事故或故障隐患，为问题处理争取更多时间，提高泵站运行综合效率和效益，达到全面的自动化远程测控目标，实现“无人值班、少人值守”。目前大中型泵站一般都配置了以可编程控制器为基础的计算机监控系统、水泵机组在线状态监测与故障诊断系统［7-9］、温度巡检系统、电气设备继电保护装置以及泵站视频监视系统等，为泵站“无人值班”打下了比较好的基础。但在离心泵站中目前尚缺少泵出口阀门的故障监测分析装置或系统。

本文试图解决离心泵出口阀门故障无监测的问题，以我国引黄灌区某单级双吸离心泵站为例，阐述基于泵站水锤计算的离心泵出口阀门的故障监测方法。

1 泵站供水系统及测压点布置

我国引黄灌区某泵站，泵站前池最低水位1 777.58 m，设计水位1 778.05 m，最高水位1 778.21 m；出水池最低水位1 803.43 m，设计水位1 804.18 m，最高水位18 04.51m。泵站最大净扬程为26.93 m，最小净扬程为25.22 m。

泵站安装8 台单级双吸离心泵，1、2、7、8 号水泵型号HS700-600-600A，设计流量1.137 m3/s，设计扬程28.88 m，额定转速970 r/min，配套异步电动机功率500 kW。3、4、5、6 号水泵型号HS900-800-850B，设计流量1.7 m3/s，设计扬程29.41 m，额定转速730 r/min，配套异步电动机功率710 kW。

1、2、3 号水泵为一并联组，4、5 号水泵为一并联组，6、7、8号水泵为一并联组。水泵出水支管为钢管，管径800 mm；总管为钢筋混凝土管，管径1 600 mm。泵站供水系统图如图1所示，总管管中心线纵剖面布置如图2所示。

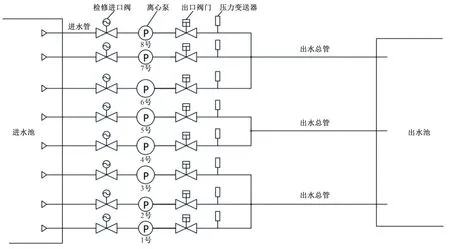
图1 泵站供水系统图Fig.1 Water supply system diagramof pumping station

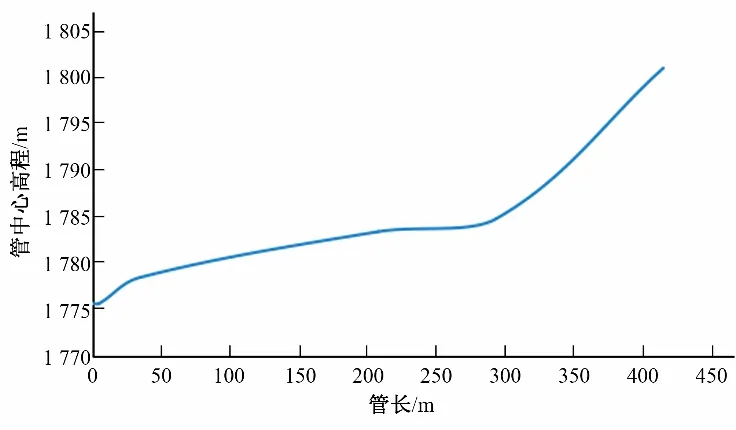
图2 总管纵向管线图Fig.2 Longitudinal pipeline diagram of manifold

不妨以1、2、3 号泵并联组为例，在1、2、3 号水泵出水支管设定点上分别安装1 只MPM489 型压阻式压力变送器，量程为1 MPa，设定点位置距泵出口阀门中心线0.93 m，测压点位置高程为1 776.07 m，如图3所示。

图3 测压点位置图（高程：m；其他：mm）Fig.3 Location of pressure transmitter

考虑到泵站抽引的黄河水中泥沙含量较大，泵出口阀门选用液控半球阀，阀径800 mm，该型阀门比较适用于在含有杂质、颗粒状等杂物的介质管道中做截流作用。其关闭规律是：从全开90°到15°快关历时9 s，从15°到全关0°慢关10 s，如图4 所示，当阀门关到15°时进行开关停机操作。

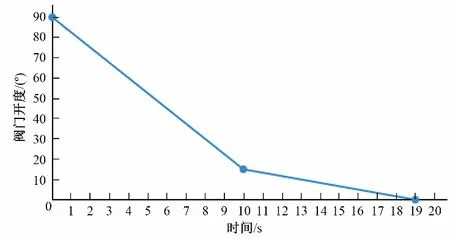
图4 泵出口液控阀门关闭规律Fig.4 Closing law of hydraulic control outlet valve of pump

2 泵系统水锤计算

2.1 水锤计算特征线法

（1）特征线相容方程。描述任意管道中水流运动状态的基本方程为：

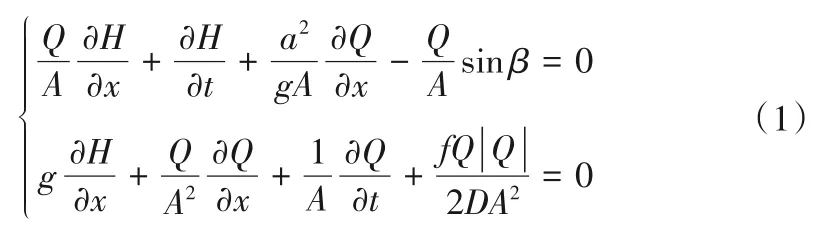
式中：H为测压管水头；Q为流量；D为管道直径；A为管道截面积；f为摩阻系数；a为水锤波速；g为重力加速度；β为管轴线与水平面的夹角；t为时间变量；x为沿管轴线的距离。

方程组（1）可简化为标准的双曲型偏微分方程，从而可利用特征线法将其转化成同解的管道水锤计算特征线相容方程，其中摩阻项用线性隐式格式近似，具有二阶精度；采用交错网络进行计算，通过调整波速来保证进、出水管的计算时间步长一致［10］。

对于长度L的管道A-B，其两端点A、B边界在t时刻的瞬态水头HA(t)、HB(t)和瞬态流量QA(t)、QB(t)可建立如下特征线相容方程：

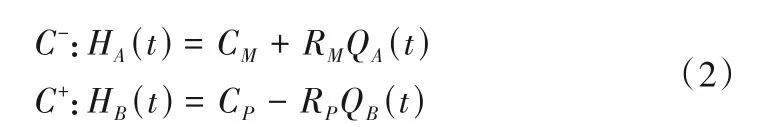
式 中 ：CM=HB(t-kΔt) -(a/gA)QB(t-kΔt)，RM=a/gA+R|QB(t-kΔt)|；CP=HA(t-kΔt) -(a/gA)QA(t-kΔt)，RP=a/gA+R|QA(t-kΔt)|；Δt为计算时间步长；ΔL为特征线网格管段长度，ΔL=aΔt（库朗条件）；k为特征线网格管段数，k=L/ΔL；R为水头损失系数，R= Δh/Q2；其他符号意义同方程组（1）。

（2）水泵节点控制方程。水泵节点控制方程包括水头平衡方程与机组转动力矩平衡方程。

①水头平衡方程。设水泵进口、阀门出口节点编号为1、2，则水头平衡方程为：

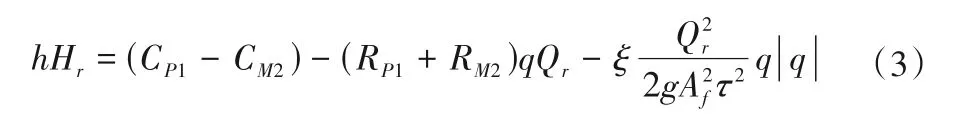
式中：Hr为额定工况水泵扬程；Qr为额定工况水泵流量；h为水泵扬程相对值，采用水泵全特性曲线确定，h=，H为水泵扬程；q为水泵流量相对值，q=，Q为水泵流量；τ为无因次流量系数，它是阀门开度的非线性函数，一般以离散数据或曲线表示；Af为阀门处管道截面积；ξ为阀门全开时的阻力系数；其他符号含义同式（2）。

②机组转动力矩平衡方程。

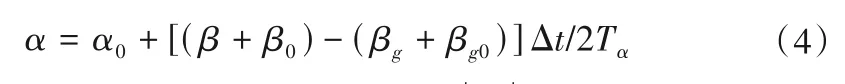
式中：Tα为机组惯性时间常数；GD2为机组转动惯性力矩；nr为额定工况机组转速；Mr为额定工况机组动力矩；α为水泵转速相对值，α=为水泵转速；β 为机组动力矩相对值，β=，M为机组动力矩，采用水泵全特性曲线确定；βg为机组转动阻力矩无量纲值；α0、β0、βg0为分别为α、β、βg的前一计算时步的值；其他符号含义同式（2）。

（3）求解方法。水锤计算一般从初始稳定运行状态开始，即取此时t= 0，取为初始值。然后按特征线法计算下一个时刻管道节点和水力元件的H与Q，一直计算下去就可得到所有管道节点和水力元件的H和Q的随时间变化过程。测压点是计算管道节点之一，从而可以计算得到测压点的压力变化过程。

对管道进行分段，对每个管段内点列写C-与C+特征线相容方程，均只有两个未知数，可以求解得到每个节点的。

对于水池可以列写一个特征线相容方程，再结合水池水力元件的一个边界条件联列计算，也可以求得H与Q。

对于水泵及阀门水力元件可以列写两个特征线相容方程，列写水头平衡方程和力矩平衡方程。水泵全特性曲线按照SUTER法表达［10］，式（3）与式（4）中的h与β均是自变量α与q的函数，从而式（3）与式（4）构成了以自变量α与q的非线性方程组，用Newton-Raphson 迭代方法求得对应计算时刻的α与q及h，可得到不同时刻水泵进口、阀门出口的H和Q。

2.2 泵站最大净扬程工况正常停机水锤计算

经计算，3 号泵的比转数为194，水锤计算时近似采用现有资料可查得的比转数175 的全特性曲线。图5 是经水锤计算得到的1、2、3 号泵并联组在最大净扬程工况下仅运行3 号泵正常停机时测压点测压管水头的变化过程线Hcmax（t），泵出口阀门关闭规律如图4 所示。图5 中t=0 时刻对应的是阀门开始关闭时刻。

图5 泵站最大净扬程工况仅运行3号泵正常停机测压点测压管水头变化过程线Fig.5 Curve of pizeometric head of pressure measuring point with time under maximum net head when normal stop of only operating No.3 pump

2.3 泵站最小净扬程工况正常停机水锤计算

对泵站最小净扬程工况进行水锤计算，可得到仅运行3#泵正常停机测压点测压管水头变化过程线Hcmin（t），如图6所示。

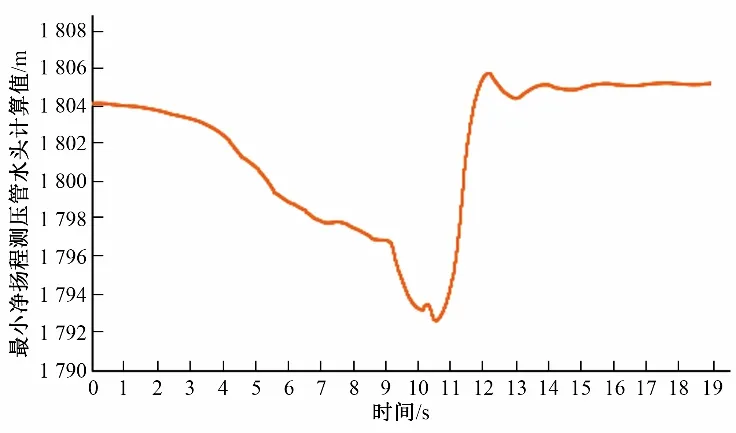
图6 泵站最小净扬程工况仅运行3号泵正常停机测压点测压管水头变化过程线Fig.6 Curve of pizeometric head of pressure measuring point with time under minimum net head when normal stop of only operating No.3 pump

3 泵正常停机试验与数模计算结果验证

泵站最大净扬程工况下，1、2、3 号泵并联组仅运行3 号泵的情况下进行水泵机组正常停机试验，泵出口阀门关闭规律如图4 所示，测压点压强水头随时间的变化曲线，如图7 所示。图7 中数据来自该泵站计算机监控系统，时刻0 点为泵出口阀门开始关闭时刻：2019年8月24日15时54分2秒。

图5 水锤计算条件与上述试验工况相同，将图5 的测压点测压管水头Hcmax（t）减去测压点位置高程就可得到压强水头pcmax（t），如图7 所示。从图7 中可以看出，两者在阀门动作的19 s 时间内压力数据基本接近，表明水锤数值计算结果是比较可靠的。

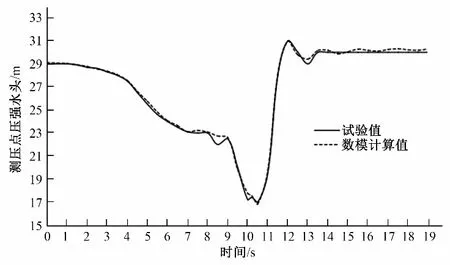
图7 泵站最大净扬程下仅运形3号泵正常停机下测压点压力变化过程线Fig.7 Curve of pressure head of pressure measuring point with time under maximum net head when normal stop of only operating No.3 pump

4 泵出口阀门故障的判断依据

将图6 最小净扬程工况下的测压管水头Hcmin（t）减去测压点位置高程就可得到压强水头pcmin（t），从而可求得最大净扬程工况与最小净扬程工况水锤计算得到的压强水头差的平方和ε，即：

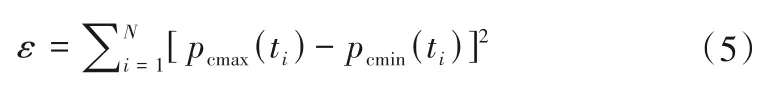
式中：i为计算时段内不同离散时刻，1，2，…，N。可取从阀门开始关闭时刻开始，到阀门完全关闭时刻结束，作为计算时段，时间步长可取1 s。

当泵出口阀门关闭规律不变化时可测得泵站实际运行净扬程工况下的测压点压强水头过程线ptnom（t），可求得与最大净扬程工况水锤计算得到的压强水头之间差的平方和E，即：

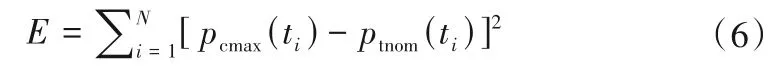
在泵出口阀门关闭规律相同条件下，泵站实际运行净扬程是在最大净扬程与最小净扬程之间，从而有E ≤ε。如果改变关闭规律，比如快关时间增大1 s，慢关时间减少1 s，总关闭时间不变，进行水锤计算，因为此时的压力变化过程与阀门正常关闭时的错位了，这时计算出的E 值将远大于正常关闭计算得到的E值。也就是说如果根据阀门关闭过程中实测压强水头值计算得到的E值大于ε，则可以认为阀门关闭规律不同于图4所示的正常关闭规律，进而可以判断阀门出现了故障，比如因密封失效使得液压系统漏油导致操作机构出现动作故障。

经计算，用图7 的试验值代入式（5）计算得到的ε 值是用图7 的水锤计算值计算得到的ε 值的0.96 倍，从而可以得到最大净扬程时实测值比计算值略小，进而得到在最小净扬程时实测值也比计算值略小。监控E值是用最大净扬程下水锤计算值与实测压力值计算的，如果实际运行在最小净扬程下则计算得到的E值将大于ε。如果不对ε做放大修正，则会得出阀门有故障的错误结论。综合考虑水泵全特性曲线、数值计算和采集数据等方面的误差，对式（5）计算得到的ε 进行修正，一般可放大1.1倍。

5 结 论

泵出口液控阀门是高扬程离心泵站的关键设备，要真正实现泵站“无人值班、少人值守”运行管理模式，就必须建立监测对象全面、功能完备的泵站状态监测与故障诊断系统，但目前的故障监测对象中尚缺少离心泵出口液控阀门。

以某引黄灌区双吸离心泵站为工程实例，本文提出了一种离心泵出口液控阀门故障监测方法。基于泵系统水锤计算结果，构建了泵站最大净扬程和最小净扬程工况下各计算时刻测压点压力差的平方和，以此为基础提出了离心泵出口液控阀门的故障监测指标值ε。当实际运行测得的压力与最大净扬程工况水锤计算得到的压力值之间差的平方和E 大于ε 时，则可以判断泵出口液控阀门存在故障。经工程实际应用验证，说明该方法是行之有效的。

本文以三台离心泵并联组为研究对象，对只有一台泵运行情况下该泵正常停机过程出口液控阀门故障的监测方法进行了研究，该方法同样可用于其他不同运行水泵机组组合，比如三台泵并联组两台泵运行情况下其中一台泵停机；两台泵并联组两台泵都运行情况下其中一台泵停机等，但故障判断标准值ε是不同的，需要经水锤计算确定。