受上游调控影响的水库入库流量预报方法研究

黄 馗，穆振宇，艾学山，3，4，陈森林，3，郭佳俊，丁 杰

（1.广西电网电力调度中心，广西 530013；2.武汉大学水利水电学院，武汉 430072；3.武汉大学水资源与水电工程科学国家重点实验室，武汉 430072；4.海绵城市建设水系统科学湖北省重点实验室（武汉大学），武汉 430072）

0 引 言

在水库调度过程中，入库流量计算是最重要的基础工作之一，水库洪水预报调度方案的编制、水库调度图的编制、水库调度经济评价以及水库洪水调节演算等都需要入库流量资料［1］。

水库入库流量一般采用水量平衡方法进行反推计算，目前大部分水库均采用静库容方法计算，利用水位库容关系曲线计算开始和终止时刻的水位对应的水库库容，由此得到该时段蓄水量的变化，同时，计算该时段水库总的出库水量，利用水量平衡原理，得到水库在该时段内的总入库水量，再与时段长相除，得到该计算时段内的平均入库流量［2］。该方法体现了水量平衡原理、流量连续性原理等主要规律，但由于计算过程中出库流量与时段库容变化量是依据库容曲线、泄流特性曲线及机组耗流量特性曲线等计算得到，故会因水位波动、各曲线拟合误差、时段长度等因素影响，使得最终得到的入库流量结果具有不可忽略的偏差，而在梯级水电站水库调度过程中，该偏差会随着计算的延续而不断扩大，进而演变成梯级水电站之间的水量不平衡问题，比如可能出现两种极端情况：区间径流系数大于1.0或为负值。

另一方面，由于调峰电厂需要随时调整负荷，其变动会引起发电流量的变动，同时由于测量误差和曲线误差等原因，通过插值等方式得到的时段库容变化量也不准确，二者共同作用使得短历时内计算所得到的入库流量数据波动很大，在其曲线上表现为明显的“锯齿”现象［3］，极不利于后续调度过程的实施，然而，在计算时段较长时，锯齿现象表现的不明显，这一是因为随着时间段的增加，各种影响入库反推的误差会相互抵消［4］，二是在长时段计算中发电流量等因素的变动减小，误差会被均化。

为减少入库流量数据中的锯齿现象，唐海华等［1］提出对库区河道进行分段优选，并根据各分段静库容曲线和代表水位计算入库流量，使得其波动幅度显著减小；武炜等［4］从入库流量反推方式出发，提出使用五点三次平滑算法对入库流量进行反推从而有效降低入库流量计算过程中的干扰。另一方面，梯级水电站之间的水量不平衡问题是由入库流量反推中的误差演变而来，采取物理或数学模型进行入库流量预报可以有效避免此误差的发生，基于此思想，刘晓阳等［5］基于降雨径流模型对梅山水库入库流量进行模拟，体现出降雨在径流模拟和预报中的重要性；康玲等［6］基于Morlet 小波对丹江口水库入库流量周期性进行分析并揭示了入库流量的多尺度震荡特性和周期性变化规律；刘章君等［7］构建Copula-BFS 模型并以三峡水库汛期入库流量概率预报为例对模型进行检验，为入库流量预报提供了一种新型途径；李茂贵等［8］建立了针对酒埠江水库入库流量的逐步回归预报模型；Herbert 等［9］利用深度学习模式进行长时期的入库流量预报，有效提高了入库流量预报的精度；Zhang等［10］基于多种模型开发出一种机器学习算法并用于水库入库流量的预报，取得了一定成果。然而，上述方法虽然在一定程度上解决了出库流量锯齿现象以及误差演变为水量不平衡问题，但是，在短时段预报中上述方法的预报精度还不能有效满足调度要求，同时，运用数学模型或算法进行预报难以反映流域站点间隐含的物理机制，说服力不足。

由此可见，流域梯级水电站之间水流演进计算存在两个方面的问题，一是因库容曲线、泄流特性曲线及机组耗流量特性曲线等不够精确，计算的出库流量和时段库容变化量不可避免的存在误差，从而导致梯级水电站之间的水量不平衡问题（如区间径流系数大于1.0 或为负值），二是短时段计算所得到的入库流量过程锯齿现象严重。针对这两个问题，本文提出一种受上游水库调控影响的日时段入库流量预报方法，将入库流量分为上游水库出库流量与区间汇流两部分，以日为时段长，应用API 模型计算区间产汇流过程，并在上游水库出流的河道演算中引入修正系数处理区间来水或引水问题，通过郁江流域西津电站的实际应用进行检验。

1 日时段入库流量预报方法

日时段入库流量预报方法的基本思路是：以日为时段长，以需要预报的水电站上游水库的出库流量、区间降雨量和水电站控制面积为基础，以水库反推的入流数据作为拟合标准进行水库日平均入库流量的模拟计算，具体计算步骤如图1所示。

图1日时段入库流量预报方法计算流程图Fig.1 Calculation flow chart of daily inflow forecast method

首先，根据区间降雨量等数据进行区间产流计算，同时对上游出库流量进行修正；其次，对区间产流进行汇流计算，对修正后的上游出库流量过程进行河道汇流计算；最后，将这两个过程叠加作为下游水库的日时段入库流量过程。

1.1 区间产流计算方法

区间流域产流计算应用API 模型［11］，流域前期影响雨量计算公式为：

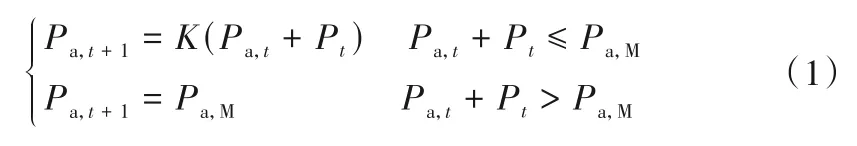
式中：Pa，t+1为t + 1时段前期影响雨量；K为消退系数；Pa，t为t时段前期影响雨量；Pa，M为流域最大前期影响雨量；Pt为t 时段降雨量。在长时段计算中初始前期影响雨量可设置为0。

假设时段径流系数βt与Pa，t、Pt的关系为：

式中：α 为指数参数，表示由降雨转化为径流的转换率，作为参数需要率定。

则t时段降雨所形成的径流深Rt为：

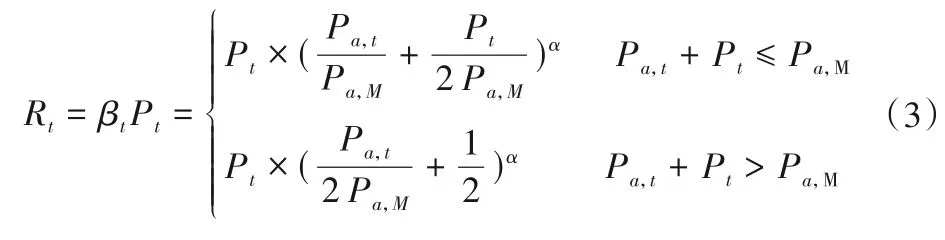
则t时段由降雨形成的总流量Qt为：

式中：A为该计算水电站所控制流域面积；As为计算水电站上游电站控制流域面积。

1.2 上游水库出库流量的修正方法

上游出库流量数据是由出力、水位、闸门开度等数据计算，在计算过程中经常会用到曲线插值计算，并且往往将一个时间点测得的瞬时值作为该时段的平均值用于计算，由于曲线的精度问题以及计算方法所产生的误差，导致上游出库流量不太准确，同时水电站之间还存在区间来水或引水问题，故以下游入库流量数据为标准，设置修正系数aQc 对上游水库的出库流量进行修正，即假设t时段能够到达下游的实际流量：

式中：Qc，t为t时段上游出库流量。

1.3 基于汇流系数法的日时段汇流计算方法

上游水库出库流量的河道汇流演算和区间汇流演算，可以应用赵人俊教授于1962年推导出的马斯京根分段连续演算汇流曲线［12］，即n个单元河段单位入流的出流过程为：

其中：

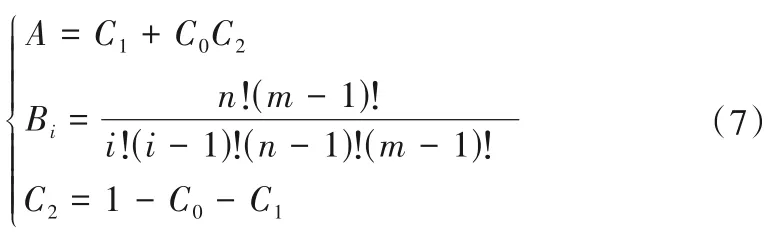
如果将C0、C1、n 作为参数（其中n 为整数，C0、C1为0 到1 之间的小数），应用式（6）和式（7）即可得到汇流系数过程φ0，n～φm，n，如图2所示，为了保证水量平衡，m的取值应满足：

图2 汇流系数过程示意图Fig.2 Schematic diagram of confluence coefficient process

由于区间汇流与河道汇流机制不同，需要分别率定区间汇流系数（φ0，n～φm，n）以及河道汇流系数

1.4 入库流量合成计算方法

t时段由区间降雨形成的入库流量ΔQR，t：

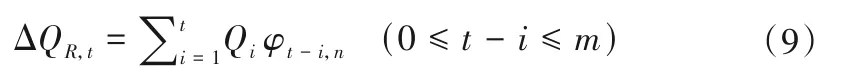
t时段由上游出库流量形成的入库流量ΔQc，t：

则t时段计算水库的日平均入库流量QAr，t为：

1.5 参数率定与检验

该入库流量预报方法需要率定的参数见表1和表2。

表1 产流及流量修正参数Tab.1 Parameter table of runoff generation and runoff conversion

表2 汇流参数Tab.2 Parameter table of runoff concentration

入库流量数据的不准确体现在与实际流量之间的误差以及锯齿现象，但随着计算时间推移，误差能在一定程度上相互抵消，故在长计算期内，历史入库流量数据仍能代表站点的实际入流过程以及实际入库总水量，故本文以历史入库流量数据作为拟合标准。根据资料情况划分率定期与检验期，考虑到各个参数之间共同对结果造成影响，所以本文采用分步率定，步骤如下：

（1）将计算期内修正后上游出库总水量与区间产流总水量之和与实际入库总水量的差值绝对值最小作为目标函数，用于率定产流及出库流量修正参数（见表1），其形式为：

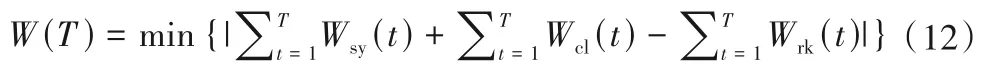
式中：Wsy(t)指t 时段内经过修正后的上游出库水量；Wcl(t)指t时段内降雨产流所形成的水量；Wrk(t)指t 时段内的实际入库水量。

（2）将计算期内最后得到的各时段模拟入库流量与各时段实测入库流量的纳什效率系数作为拟合标准，用于率定汇流参数（见表2），其形式为：

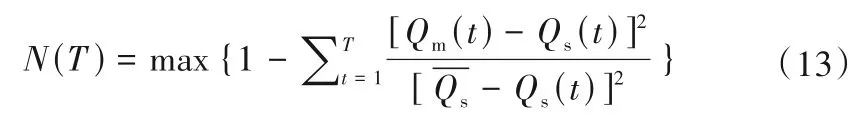
式中：Qm(t)表示t时段内的模拟入库流量；Qs(t)表示t时段内的实测入库流量表示计算期内实测平均入库流量。

2 实例应用

2.1 实例概况

郁江位于云南省东部和广西壮族自治区南部，是西江流域一级支流，发源于云南省文山壮族苗族自治州广南县，于广西桂平市注入西江浔江段，郁江流域水库群有12 座主要电站，其中西津电站位于广西横县，是一座以发电为主，兼顾航运的水电站，在南宁市下游约100 km，其上游有属右江支流的金鸡滩水电站和属左江支流的山秀水电站，具体关系见图3。

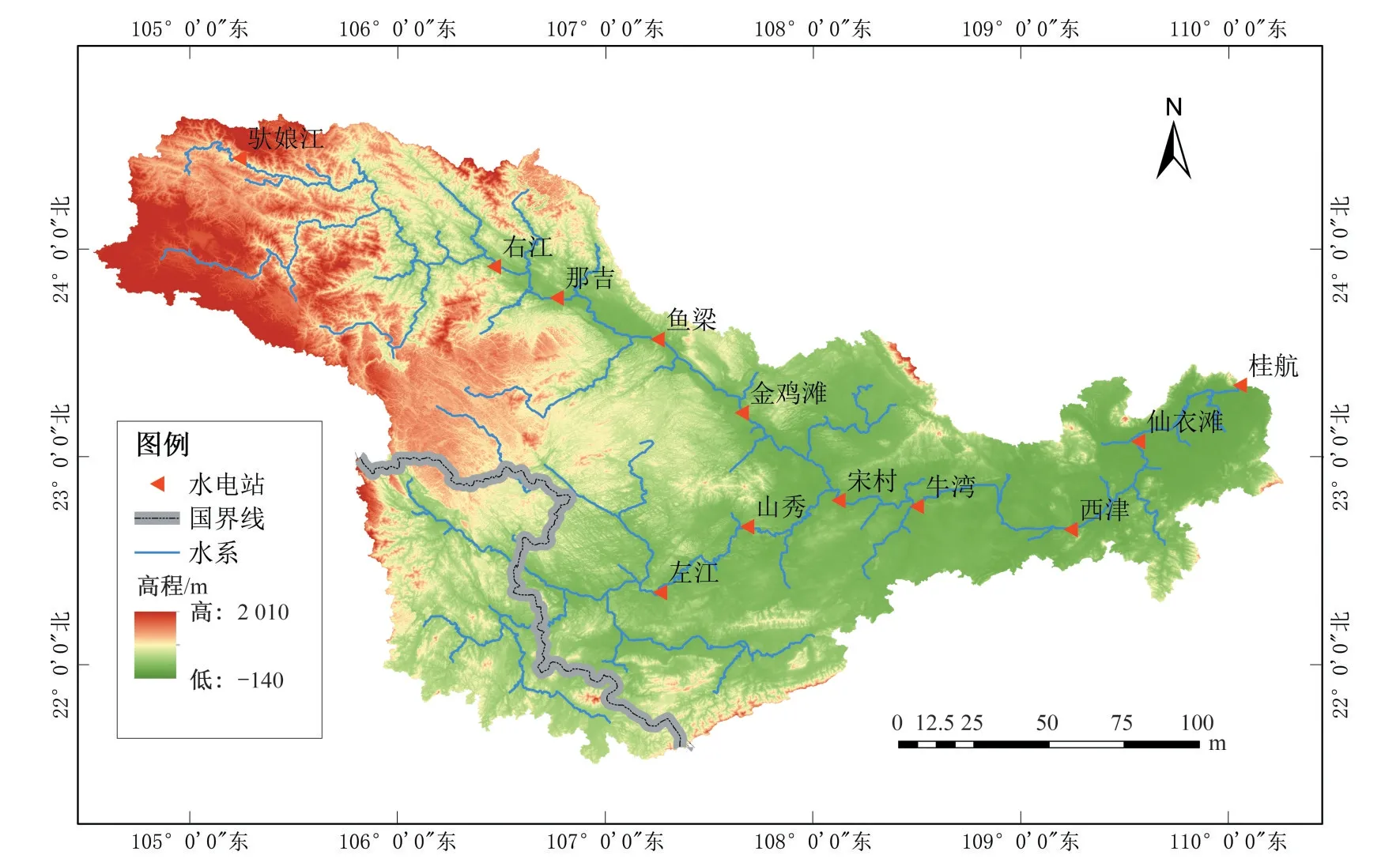
图3 西津水电站上下游关系示意图Fig.3 Relationship between upstream and downstream of Xijin hydropower

2.2 参数率定及统计结果

选取西津水库2013-01-01-2020-01-01 的日降雨量、入库流量以及上游两座水库的出库流量，以2013-01-01-2017-12-31 作为率定期，2018-01-01-2020-01-01 作为检验期，以纳什效率系数作为模型的评判标准，由于西津上游存在两个电站，故率定两套流量修正参数以及河道汇流参数。

本文采用遗传算法［13］根据节1.5目标函数及率定步骤进行参数率定，产汇流及流量修正系数参数结果见表3、4 以及图4、5及图6。

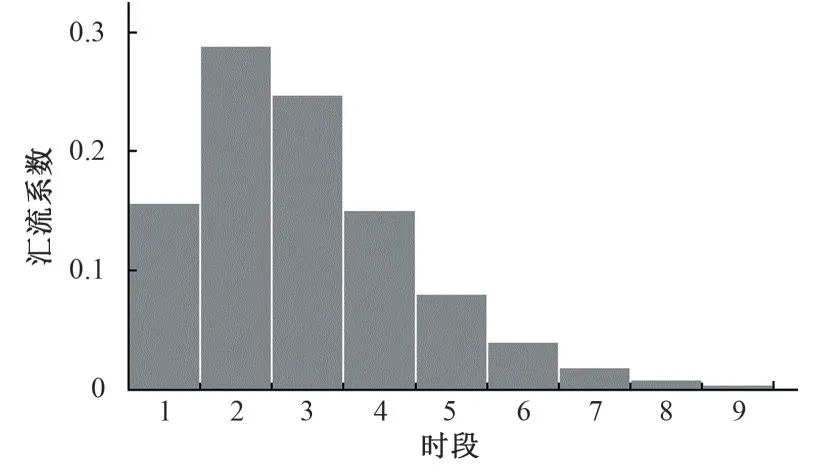
图4 区间流域汇流系数Fig.4 Concentration coefficient of interval watershed

图5 金鸡滩水电站出库河道汇流系数Fig.5 Concentration coefficient of Jinjitan hydropower station outflow channel

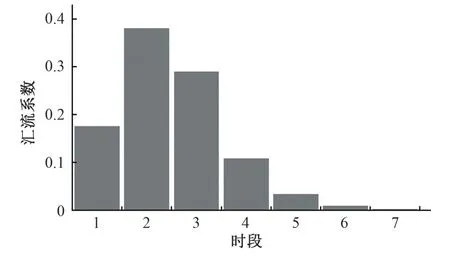
图6 山秀水电站出库河道汇流系数Fig.6 Concentration coefficient of Shanxiu hydropower station outflow channel

由率定参数计算西津水电站各时期及逐年纳什效率系数，结果见表5 和图7 所示。2013年和2014年的径流模拟结果见图8和图9所示。

图7 各年纳什效率系数Fig.7 NSE of each year

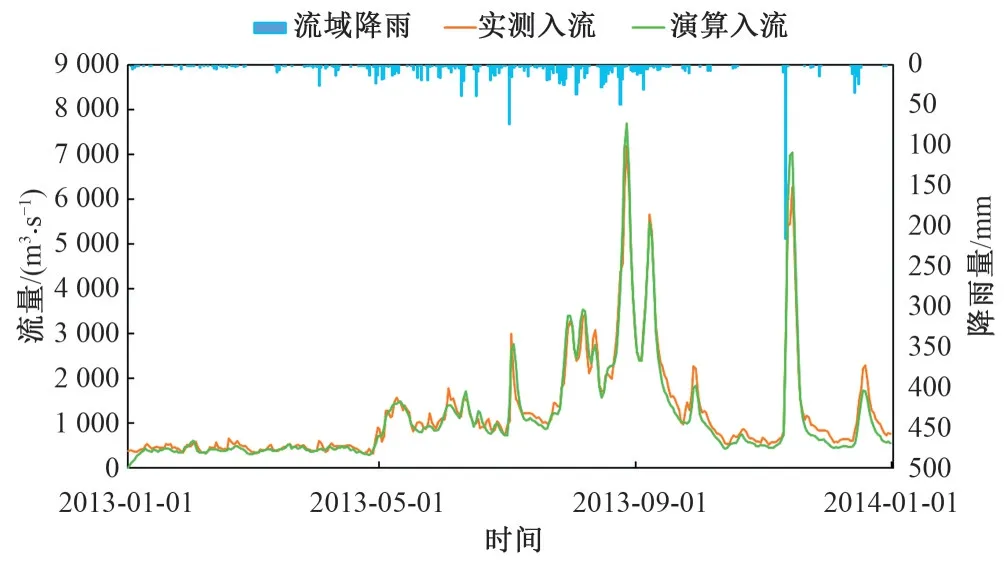
图8 西津水库2013年径流模拟结果Fig.8 Simulation results of runoff in Xijin Reservoir in 2013

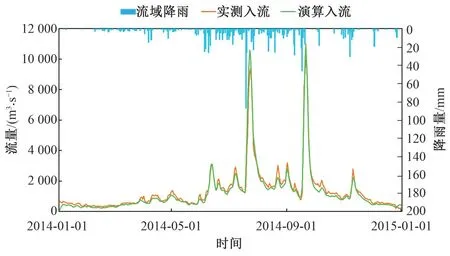
图9 西津水库2014年径流模拟结果Fig.9 Simulation results of runoff in Xijin Reservoir in 2014

2.3 成果分析

本方法通过对上游出库流量进行修正，并基于降雨进行区间产流计算，最后将这两部分采取汇流计算得到模拟入库流量数据，计算步骤简洁且符合水文学基本原理，率定得出的降雨产流参数以及汇流系数很好地代表了该流域区间及河道的汇流特征，由于2016年短时强降雨较多，使得该年的模拟精度相较其他时段略有下降，但在率定期本方法模拟计算纳什效率系数达到了0.943，检验期纳什效率系数达到了0.914，取得了很好的计算效果，同时本方法有效解决了梯级水电站之间的水量不平衡问题，形成的流量过程也避免了传统方式所产生的锯齿现象。

表4 汇流参数率定表Tab.4 Calibration table of runoff concentration parameter

表5日尺度纳什效率系数Tab.5 NSE in each period of daily scale

2.4 参数敏感性分析

根据各参数特性，以率定参数为基础，采取固定其他参数，在一定范围内变动某一参数方式进行敏感性分析，参数变动范围见表6、7，敏感性分析结果见图10、11和图12。

图10 纳什效率系数与消退系数K关系Fig.10 Relationship of regression coefficient K and NSE

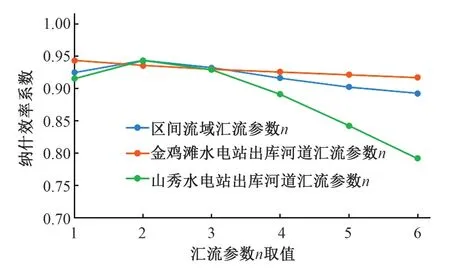
图11 纳什效率系数与汇流参数n关系Fig.11 Relationship of runoff concentration coefficient n and NSE

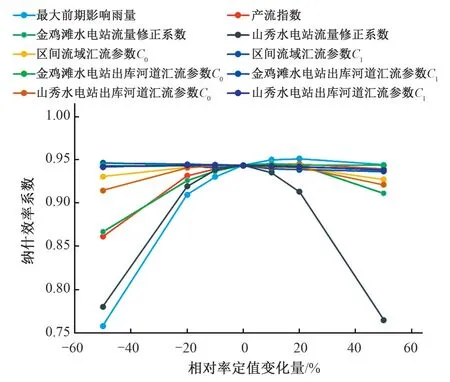
图12 纳什效率系数与产流参数、出库修正系数及部分汇流参数关系Fig.12 Relationship of runoff generation，outflow revised，part of runoff concentration coefficient and NSE

表6 消退系数及部分汇流参数取值Tab.6 Values of regression coefficient and partial concentration parameters

通过参数敏感性分析研究可得到以下结论：

（1）由于实际资料中西津水库上游出库水量之和小于该站入库水量之和，缺失的水量由降雨过程来弥补。消退系数K最为敏感，其对流域降雨产流过程具有重要影响，纳什效率系数随前期最大影响雨量Pa，M、产流指数α变动所产生的变幅也较大。

（2）山秀站年平均流量要高于金鸡滩站年平均流量，故山秀水电站出库流量修正系数aQc*、山秀水电站出库河道汇流参数n*变动所产生的变幅要比金鸡滩站对应参数变动所产生的变幅稍大。

表7 最大前期雨量、产流指数、出库修正系数以及部分汇流参数取值Tab.7 Values of PaM，α，and partial concentration parameters

（3）以纳什效率系数为标准，相较于上游出库部分，降雨产流及汇流部分对整个模拟过程有更强的影响。

3 结 论

通过理论分析及在广西郁江流域西津水库的实例计算，得到如下结论：

（1）本文提出的日时段入库流量预报方法以水量平衡理论、API模型以及马斯京根汇流系数法为理论基础，以上游出库流量和区间降雨产流作为入库流量两个组成部分，并通过出库流量修正解决上游出库流量数据不准确以及区间来水或取水情况不明确等实际问题，符合水文学基本原理，且对现有资料运用充分，有效解决了梯级水电站之间水量不平衡问题以及传统方式所产生的流量过程锯齿现象。

（2）参数敏感性分析结果表明，消退系数K对于纳什效率系数值有着重要影响，为参数选取与率定提供了必要指导。

（3）本方法所需率定参数少，率定速度快，在实例应用中，率定期模拟计算纳什效率系数达到了0.943，检验期纳什效率系数达到了0.914，实现了很好的模拟效果，对水电站水文预报以及水库调度方案的制定与实施具有积极意义和重要参考价值。