铺层角度和弹头锥角对CFRP层合板抗侵彻性能的影响
陈 波 潓
(东北大学理学院,110819,沈阳)
0 引言
CFRP复合材料是先进复合材料中的重要增强材料,因其具有轻质量、高强度、耐腐蚀、耐磨损、耐疲劳等特性,被广泛应用于航空航天领域,是飞机、火箭、航天飞行器制造不可或缺的材料。面对复杂的飞行环境,CFRP复合材料经常会受到鸟撞、冰雹等高速冲击,其很容易发生基体开裂、分层、纤维断裂等损伤。因此,深入研究在高速冲击作用下,改变铺层角度和弹头锥角对层合板的弹道极限速度和失效模式的影响显得尤为重要。
Topac等[1]通过圆柱形落锤冲击层合板实验,并对实验进行有限元模拟,数值结果与实验获得的实时应变场值、失效机制和失效顺序吻合较好;Wang等[2]采用二级轻气炮实验和数值方法研究了不同厚度碳纤维复合材料层合板在低速和高速冲击作用下的能量吸收率,发现在较高速度的冲击作用下薄碳纤维布层合板具有优势,在较低速度的冲击作用下厚碳纤维布层合板具有优势;彭捷等[3]通过搭建实验平台,研究了弹头以不同冲击速度作用下,碳纤维复合材料层合板损伤区域面积、能量吸收率、损伤形式和能量吸收机制的变化规律,发现弹头剩余速度和弹头剩余速度变化率与初始速度有关;Karakuzu等[4]进行玻璃纤维/环氧树脂复合材料的低速冲击试验和相关数值模拟,分析不同冲击能量、冲击器质量、冲击速度下复合材料板的冲击损伤特性,数值计算结果与实验结果吻合较好;顾善群等[5]通过空气炮冲击实验研究了在高速冲击作用下树脂韧性和碳纤维复合材料的内部损伤程度,并进行冲击后剩余压缩性能的比较,发现其树脂含量越高,抗冲击性能和剩余压缩性能越好。胡年明等[6]运用Ansys/LS-DYNA进行有限元仿真,研究了在不同形状弹丸的冲击作用下,不同厚度的Kevlar纤维层合板及UHMWPE层合板的变形破坏情况,指出层合板的吸能效率与弹丸的形状、板的厚度有关。Zhu等[7]建立了基于连续损伤力学的非线性有限元模型,分析了碳纤维增强铝板在不同形状弹头高速冲击下的弹道性能和损伤特性,发现弹丸的形状对冲击结果的影响与初始速度有关;Rahmani等[8]通过改变环氧树脂基体中纳米SiO2和ZrO2粒子的含量,研究在高速冲击作用下碳纤维增强铝层合板的能量吸收能力,发现在CARALL中添加合适的SiO2/ZrO2刚性纳米颗粒可以提高CARALL的冲击吸收能量;Liu等[9]采用气枪实验和有限元模拟,研究以热塑性聚醚醚酮(CF/PEEK)和热固性增韧环氧树脂(CF/环氧)为基体的碳纤维复合材料在低速和高速冲击作用下的损伤面积,其模型结果与试验测量结果得到了很好的吻合,捕捉了复合材料冲击行为的基本方面。
尽管国内外学者已经对碳纤维复合材料层合板在高速冲击作用下的损伤特性开展了一定的实验和数值模拟工作,并对提高层合板的抗冲击性能提供了建议,但是关于在高速冲击作用下采用不同铺层角度的CFRP层合板损伤特性的研究工作并不是很多,且由于实验环境复杂,所以进行相关的数值模拟工作还需进一步深入。本文利用ABAQUS软件建立CFRP层合板的有限元模型,模拟CFRP层合板在弹丸高速冲击作用下的损伤过程,通过改变层合板的铺层角度和弹头的锥角大小,分析层合板的弹道极限速度和能量损耗,并对提高层合板的抗侵彻性能提供参考。
1 有限元模型
1.1 几何模型与网格划分
选择文献[10]试验中的层合板尺寸和材料参数(表1)建立有限元模型,层合板尺寸为200 mm×200 mm×8.4 mm,铺层角度为[0°/90°]6,单层板厚度0.7 mm,共12层(图1)。由于层合板的变形和损伤主要发生在接触区,为保证计算精度,需对此部分网格进行加密,在层合板中心区域40 mm×40 mm,设置网格单元大小为2 mm×2 mm;其余区域设置网格单元大小为4 mm×4 mm。由于层合板的厚度相对于弹体长度很小,可视为薄壁结构[11],单元类型为S4R(图1(a)),共3 760个节点,3 600个单元。弹头为钢制锥头圆柱形,半径为3.5 mm,长径比为5.85,质量为10.306 g,密度为7 800 kg/m3,弹性模量为211 GPa,泊松比为0.3。已有实验结果表明弹头在侵彻过程中变形很小,可视为刚体,将弹头质量集中在参考点上[12],单元类型为C3D8R,采用结构化单元进行划分(图1(b)),共919个节点,780个单元。
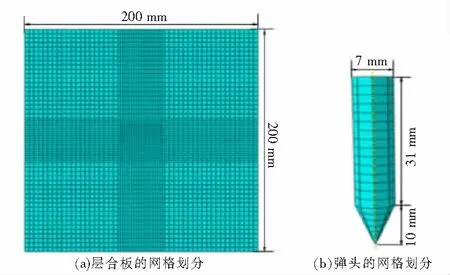
图1 网格划分

表1 复合材料性能参数
1.2 材料属性
1.2.1 材料的本构关系 此模型为正交各向异性材料,其弹性性能应满足广义胡克定律,可以得到正交各向异性线性弹性体的刚度矩阵[13]为:
(1)
其中:σi为应力,εi为应变,Cij为刚度系数(i,j=1,2,3,4,5,6)。设平面内的方向为1、2方向,厚度方向为3方向,其中独立刚度系数为9个,分别为3个方向的弹性模量Ei、3个平面的剪切模量Gij以及3个平面的泊松比ij(i,j=1,2,3),其满足的关系式为:
(2)
1.2.2 层合板损伤失效模型 在高速冲击载荷作用下,复合材料层合板具有多种损伤模式,如基体剪切破坏、纤维拉伸破坏、基体开裂等。应用合适的失效准则模拟高速冲击作用下纤维复合材料界面的力学行为是非常重要的。本文采用二维Hashin失效准则,对层合板建立渐进损伤模型,考虑纤维和基体不同的应力状态和破坏机理,其二维Hashin失效准则[14]表达式如下。
纤维拉伸失效:
(3)
纤维压缩断裂:
(4)
基体拉伸或剪切失效:
(5)
基体压缩或剪切失效:
(6)
其中:Xt为纵向拉伸强度;Xc为纵向压缩强度;Yt为横向拉伸强度;Yc为横向压缩强度;S12为1~2面内剪切强度值;S23为2~3面内剪切强度值。
1.3 相互作用和边界条件
此模型中假设弹头为连续均匀介质,采用通用接触来定义弹丸和层合板之间的接触响应,将法向行为设置为硬接触。沿层合板的外围施加固定边界条件,其所有自由度被限制为零。为将弹丸的初始撞击速度施加在弹丸的基准点上,除沿Z轴的直线运动外,其它方向的自由度均被限制(图2)。
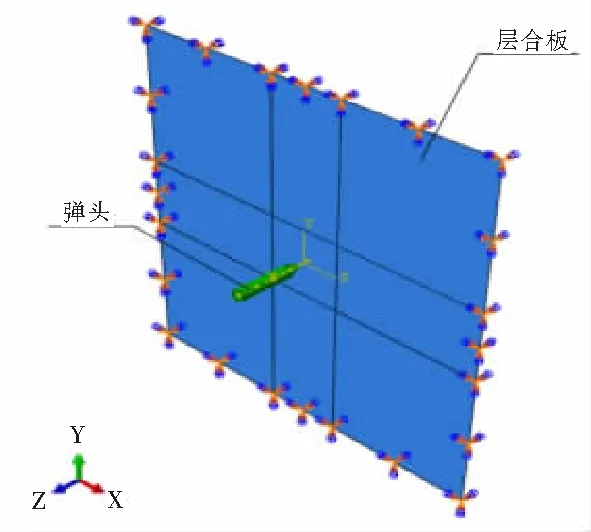
图2 边界条件
1.4 模型验证
为了验证所提出的有限元模型的准确性和有效性,本文按照第2部分提出的方法建立了文献[10]中报道的锥形弹头冲击层合板有限元模型,分别将200~900 m/s的弹头冲击层合板得到的剩余速度进行曲线拟合如图3,与文献[10]的剩余速度进行比较如表2所示,误差均在6%以内。误差产生的原因可能是一方面文献数据利用Engauge Digitizer软件进行提取,存在在系统误差,另一方面网格划分的疏密程度也会影响解的计算值。表明此模型计算数值与文献数据基本一致,可见本文建立的有限元模型计算正确,分析方法可靠,可以进一步分析不同铺层角度对层合板抗高速冲击的性能。

表2 剩余速度对比
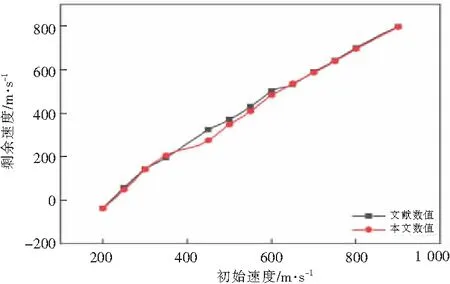
图3 本文数值与文献数值对比
2 结果分析
2.1 弹道极限速度
2.1.1 铺层角度对CFRP层合板弹道极限速度的影响 在保证层合板厚度不变的情况下,分析不同铺层角度对弹头剩余速度和损耗动能的影响,分别设置[0°/90°]6、[0°/45°/90°-45°]3、[0°/30°/60°/90°/-60°/-30°]23种铺层角度,其中30°、45°、60°指纤维的1方向与层合板纵向的夹角。通过分析弹头的剩余速度和能量损耗,研究层合板在150~600 m/s的速度冲击作用下的抗侵彻性能。本文的弹头初始速度接近于弹道极限速度,利用R-I公式[15],对弹头的初始速度和剩余速度进行拟合(图4),得到弹头的弹道极限速度:

图4 [0°/45°/90°-45°]3铺层方式的弹头剩余速度拟合曲线
(7)
式中:vr为剩余速度,vi为初始速度,vbl为弹道极限速度,a和p为模型参数,由数据拟合得到。
其它铺层方式的剩余速度与初始速度数据拟合方法与图4一致,相关的拟合结果如表3所示。
在非线性回归模型中R2越接近1,拟合效果越好。由表3可知,采用[0°/90°]6铺层方式的弹头极限速度为215.695 m/s,[0°/45°/90°-45°]3铺层方式的弹道极限速度为268.258 m/s,[0°/30°/60°/90°/-60°/-30°]2铺层方式的弹道极限速度为260.544 m/s,与文献[16]描述的一致,层合板的抗侵彻性能随层间角度呈抛物线变化,角度铺层的抗弹性能优于正交铺层。由图5(a)可以看出在弹道极限速度附近时,[0°/45°/90°-45°]3铺层方式比[0°/30°/60°/90°/-60°/-30°]2铺层方式更能提高层合板的抗侵彻性能。然而在弹头冲击速度为350~600 m/s时,采用[0°/45°/90°-45°]3和[0°/30°/60°/90°/-60°/-30°]2铺层方式的层合板对弹头的能量吸收率降低,层合板的抗侵彻性能减弱,所以适当的调节铺层角度可以提高层合板的抗侵彻性能。
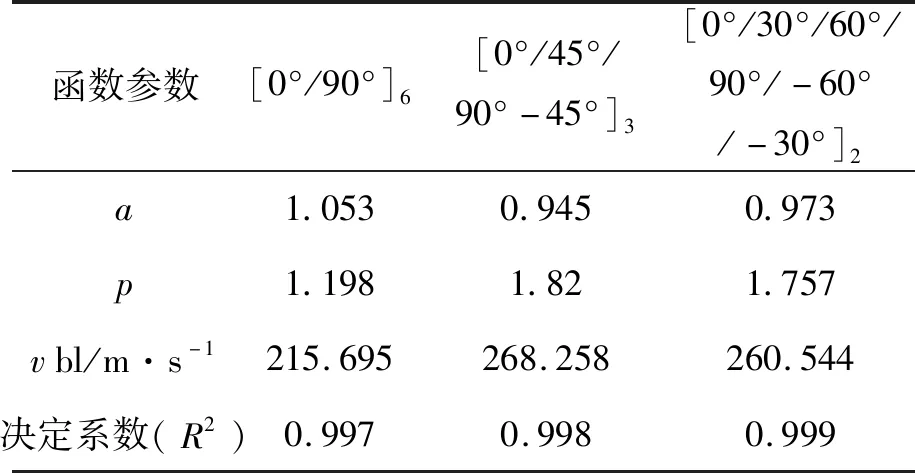
表3 不同铺层角度的模型参数和弹道极限速度

图5 不同铺层角度下初始速度与剩余速度和损耗动能关系
图5(b)是初始速度-损耗动能曲线,随着冲击速度的不断增大,弹头的能量变化经历了3个阶段,与文献[17]实验结论基本一致。第1阶段弹头回弹阶段,初始动能大于损耗动能,子弹发生反弹;第2阶段弹头侵彻阶段,初始动能几乎等于损耗动能,在150~250 m/s的速度区间内,弹头的初始动能为115~322 J,弹头的损耗动能为110~309 J;第3阶段弹头穿透阶段,初始动能大于损耗动能,弹头达到穿透层合板的极限速度,弹头的损耗动能随弹头速度的增加趋于平缓,初始动能与损耗动能呈双线性关系。
2.1.2 弹头锥角对CFRP层合板弹道极限速度的影响 研究采用[0°/45°/90°-45°]3铺层方式,通过改变锥头角度分析层合板弹道极限速度的变化规律。分别设置锥角为20°、38.6°、50°、60°和90°的弹头,且保证弹头质量一致,研究初始速度为150~600 m/s的弹头在冲击层合板后的剩余速度,并进行曲线拟合(图6)。由R-I公式(表4)可得20°锥角的弹道极限速度为245.735 m/s,38.6°锥角的弹道极限速度为242.714 m/s,50°锥角的弹道极限速度为257.806 m/s,60°锥角的弹道极限速度为235.34 m/s,90°锥角的弹道极限速度为259.567 m/s。
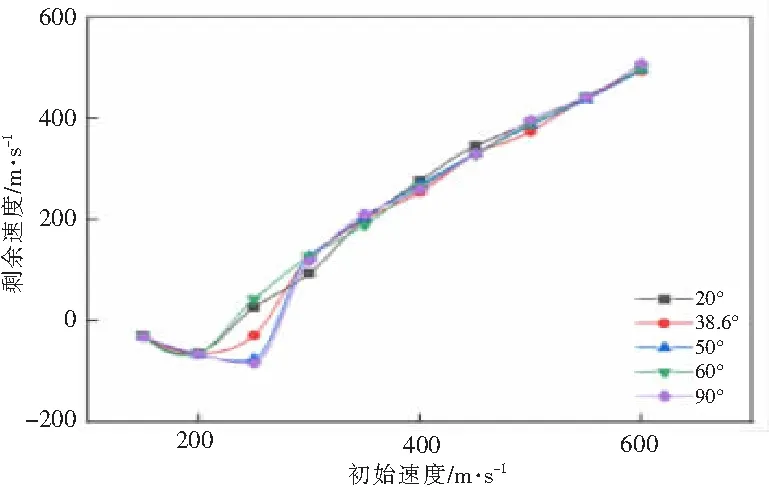
图6 不同锥角弹头初始速度与剩余速度关系
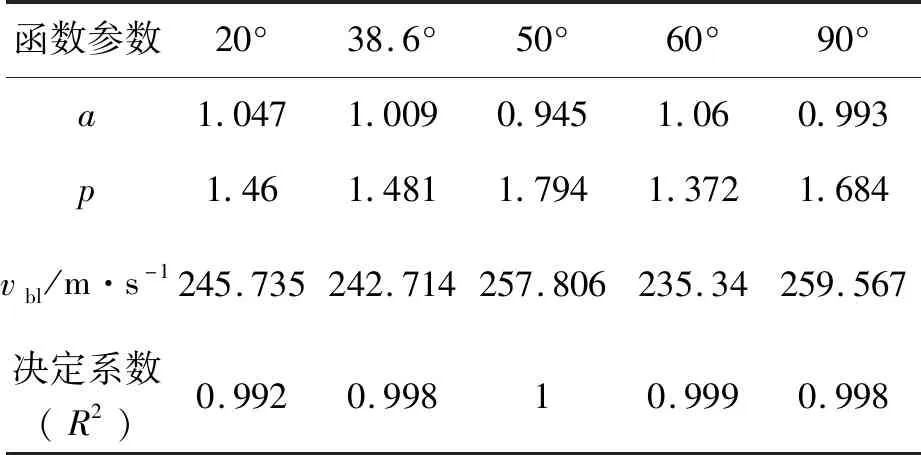
表4 不同弹头锥角的模型参数和弹道极限速度
发现在低速和高速区域,改变弹头的锥角并不能增强弹头的穿透能力。然而在弹道极限速度附近(200~300 m/s),弹头锥角的变化对层合板的抗侵彻性能有显著影响,弹头锥角与弹头的剩余速度并非线性关系,在锥角小于60°的范围内,弹头极限速度随锥角的增大而增大。在高速冲击区域,锥角的变化对弹头的穿透能力几乎没有影响。基于以上数据,当锥角为60°时,弹头的穿透能力最强。
2.2 侵彻状态
2.2.1 铺层角度对层合板侵彻状态的影响 分析初始速度为300 m/s的弹头在侵彻过程中速度变化,由图7可以看出3种不同的铺层方式,其弹头的速度变化大致经历3个阶段,第1阶段,层合板发生变形,但并没有被穿透,对弹头的阻碍作用明显,弹头速度下降的较快;第2阶段,弹头锥形部分穿孔阶段,随着时间的增加,锥头部分与层合板的接触面积逐渐增加,层合板被破坏的面积也逐渐增加,弹头速度下降的速率没有第1阶段的快,主要是因为层合板的性能已经受到了破坏,抗侵彻能力下降;第3阶段,弹头圆柱形部分穿孔阶段,这个过程弹头与层合板的接触面积基本不会发生变化,层合板对弹头的阻碍作用比较稳定,所以此阶段弹头速度逐渐趋于平稳。3种不同的铺层方式对第1阶段弹头的速度变化影响基本一致,主要差别于第2阶段(弹头锥形部分穿孔阶段),[0°/90°]6的铺层方式对弹头的抗侵彻能力较低,[0°/45°/90°-45°]3和[0°/30°/60°/90°/-60°/-30°]2的铺层方式对弹头的阻碍作用明显,弹头速度下降得较快,层合板的抗侵彻能力较强。
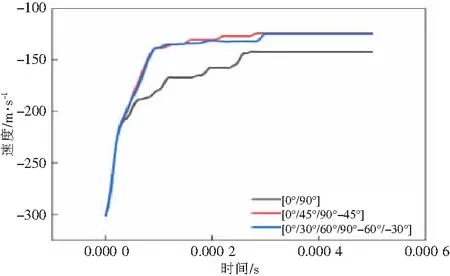
图7 不同铺层角度下弹头的速度随时间变化曲线
图8显示了[0°/30°/60°/90°/-60°/-30°]2铺层方式下,速度为300 m/s的弹头作用于层合板的侵彻状态变化。分别为t=35.2 μs、t=100.3 μs、t=145.2 μs、t=285 μs,在此过程中,层合板的应力最大值始终发生在弹头冲击区域的外围,由0°和90°轴向向外扩展,这是因为此位置基体受拉程度较大;而在冲击区域,应力值较小。随着侵彻状态的变化,应力值先增大后减小。
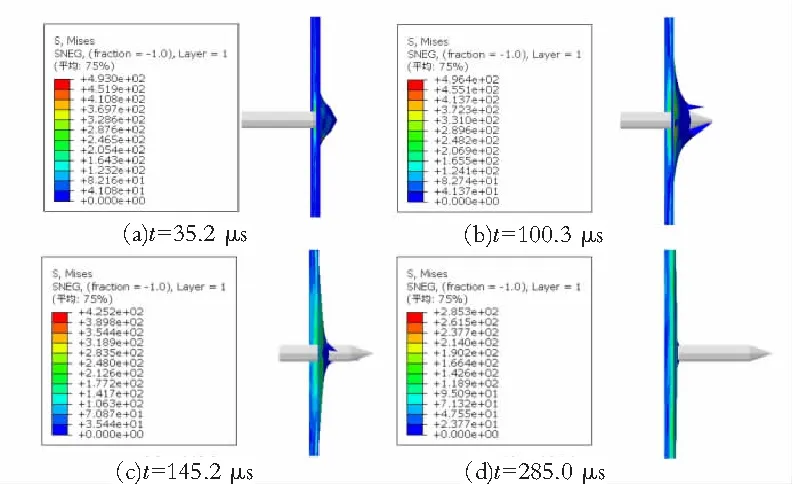
图8 弹头侵彻状态应力云图
2.2.2 锥头角度对层合板侵彻状态的影响 在铺层角度为[0°/45°/90°-45°]3时,研究锥头角度对层合板侵彻状态的影响(图9)。在层合板未被穿透时,锥角的变化对弹头速度变化率影响较小;在弹头锥角部分穿透层合板时,锥角越小,弹头速度下降越快,在t=105 μs时,锥角为38.6°的弹头锥形部分完成穿透;在t=115 μs时,锥角为60°的弹头锥形部分完成穿透;在t=115.3 μs时,锥角为90°的弹头锥形部分完成穿透。在弹头圆柱形部分穿透层合板时,锥角与弹头剩余速度并非线性关系,60°锥角的弹头速度下降得最快,其穿透能力最强。当锥角大于60°,随着锥角的增加,其速度损耗增大,但锥角与速度损耗关系比较平缓。
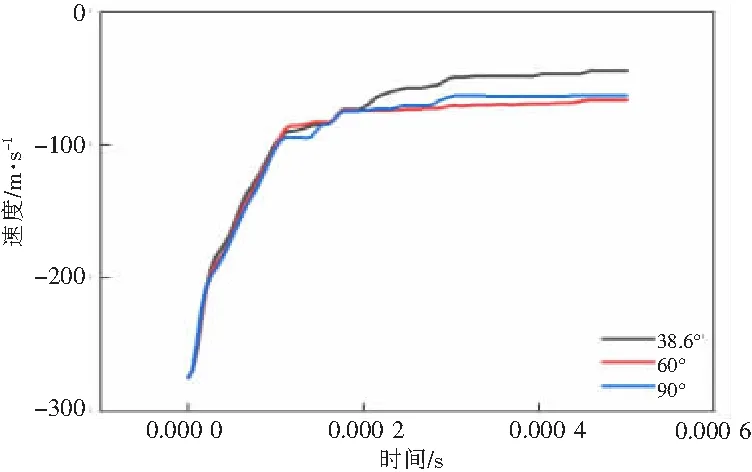
图9 不同锥角弹头的速度随时间变化曲线
2.3 损伤情况分析
在相同速度(300 m/s)、同一时刻(50.2 μs)比较不同铺层方式对纤维损伤、基体损伤和剪切损伤的影响。
3种铺层角度在同一时刻引起的损伤面积如表5所示,在冲击作用下,基体的拉伸损伤程度要大于纤维的拉伸损伤程度,由于纤维的抗拉强度高于基体材料,在承受高速冲击作用下,主要是纤维承受抗拉破坏,基体承受压缩破坏。当纤维发生拉伸破坏时,基体早已发生破坏;基体的压缩损伤程度要大于纤维的压缩的损伤程度,因为当基体发生压缩性质的损伤时,纤维由于其本身的特性,可能没有损伤或者有很小的损伤。采用[0°/90°]6铺层方式的层合板的纤维损伤和基体损伤面积比较小,而采用[0°/45°/90°-45°]3和[0°/30°/60°/90°/-60°/-30°]2铺层方式的层合板在300 m/s冲击作用下的损伤面积比较大。对于实际操作,[0°/45°/90°-45°]3的可操作性强,抗侵彻性能好,更适用于工程应用。

表5 不同铺层角度损伤面积/mm2
由图10对比发现剪切损伤的扩展趋势与铺层角度有关,[0°/90°]6铺层层合板的剪切损伤分别沿0°和90°轴向扩展,[0°/45°/90°-45°]3层合板的剪切损伤有沿0°、45°、90°的方向扩展,[0°/30°/60°/90°/-60°/-30°]6层合板的剪切损伤沿0°、60°、90°、-60°的方向扩展,对比发现采用角度铺层的层合板的剪切损伤扩展趋势比较均匀,近似圆形。在冲击速度为300 m/s的作用下,由于角度铺层引起的损伤面积比正交铺层引起的损伤面积大,所以正交铺层的应力集中现象更明显,更容易被破坏。而基体拉伸损伤、基体压缩损伤、纤维拉伸损伤、纤维压缩损伤(图11)在3种铺层方式下的扩展趋势基本一致。

图10 剪切损伤云图
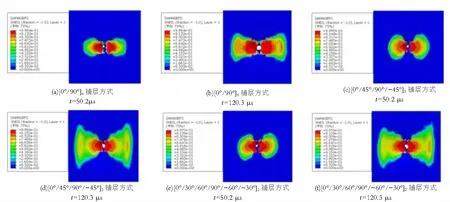
图11 纤维压缩损伤云图
3 结论
通过建立弹头冲击层合板的有限元模型,分析不同铺层角度和弹头锥角对层合板的抗侵彻性能,得到如下结论。
1)在单层板厚度保持不变的条件下,铺层角度与弹头剩余速度的关系并非线性关系,角度铺层优于正交铺层,[0°/45°/90°-45°]3的铺层方式更能提高层合板的抗侵彻性能。
2)弹头的速度变化趋势与侵彻状态有关,在弹头未穿透层合板时,弹头冲击区域外围的应力为整个冲击过程的最大值,弹头速度下降最快。
3)在300 m/s冲击作用下,[0°/90°]6铺层方式造成层合板损伤面积比较小,应力集中现象明显,而[0°/45°/90°/-45°]3和[0°/30°/60°/90°/-60°/-30°]2铺层方式造成层合板损伤面积比较大。不同铺层角度对层合板剪切损伤扩展趋势有一定影响,但对于纤维和基体的损伤扩展趋势影响不明显。
4)弹头锥角与弹头的剩余速度不是线性关系,在锥角为60°时,弹头的穿透能力最强。在低速和高速区域,锥角对弹头的剩余速度影响不大。

