通信基站新风系统负荷预测模型

易兵杰，谭平安，吴炎明，蔡 立，彭卫文

（1.湘潭大学自动化与电子信息学院，湖南湘潭 411105；2.恩杰康科技有限公司，长沙 410001）

0 引言

随着5G时代的到来，通信基站能耗增长极快。在通信基站能耗中空调散热能耗占比极大[1]。针对基站散热节能的技术主要有：空调变频改造、空调添加剂技术、新风节能（自然通风）技术[2-3]等，相较于前两种针对空调本身的方法，新风节能利用自然冷源降低空调的使用频率，节能潜能更大，对通信基站节能具有重大意义。

传统的新风系统为定风量新风系统，其风量不能根据实时温度进行调整，具有较大的局限性。变风量系统则能根据基站温度的变化来调节新风系统的送风量，其节能性能优越，极大地提高了基站的冷却效率，保守估计变风量系统比定风量系统节能30%[4]。通信基站新风系统是一个热扰动大的系统，单一的变风量控制器很难进行有效的控制[5]，容易造成控制延时问题。在控制器向执行器发出调节指令时，系统实现控制指令要经历一个时间段，可长达数分钟[6]，控制延时会导致新风的浪费和散热能耗的增加。负荷预测可以解决这类延时问题，在建筑空调领域，针对被控对象及其环境和任务存在很大的不确定性，根据智能控制理论，通过精确的负荷预测辅助科学的系统控制使空调系统散热能耗更低[7]。将负荷预测引入到通信基站新风系统中，对其散热节能也是具有重大意义的。

本文基于BP神经网络建立了一种适用于通信基站新风系统的负荷预测模型。首先对基站新风系统运行数据进行分析，利用灰色关联分析法确定新风系统负荷预测模型的输入因子。建立数据样本库以训练BP神经网络，并利用遗传算法优化BP神经网络参数，借此构建通信基站新风系统的负荷预测模型，最后通过实验对比分析验证了该模型的正确性和有效性，可以辅助通信基站新风系统实现节能运行。

1 通信基站新风系统负荷变化规律分析

1.1 工作原理

本文的研究对象是长沙某酒店通信基站，该基站占地面积17.68 m2，高3 m，如图1所示。该基站内部包括新风系统、空调和通信基站综合柜，其新风系统由进风装置、排风机和室内外温湿度传感器组成。进风装置由变频器对进风机进行无极调速，并根据风速大小均分为255个风机挡位。基站新风系统采用智能控制器实时监测室内外温度。当室内温度低于29℃时，控制器开启进风装置并根据室内外温差调节挡位引入室外新风，关闭机房空调达到节能效果；当室内温度高于29℃时，控制器关闭进风装置并启动空调。其中室内外温湿度监测点分别在出风口所在墙面的正中心和进风口处。

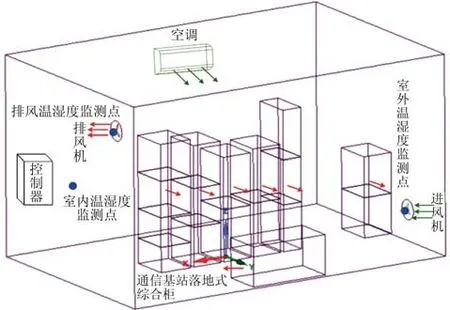
图1 通信基站新风系统基本工作原理

1.2 运行数据分析

新风系统运行数据分析是进行负荷预测的基础。基站的新风系统运行数据为2021年3月与4月中的采样数据，其中新风系统负荷由风机挡位表示。通过数据清理使数据干净、整齐，以免数据挖掘的结果受到影响后，再寻找数据的规律。为了方便分析风机挡位的规律，取其中部分挡位合并为3个挡位段。图2、3分别显示该基站在3、4月中3个挡位段对应室内外温度的负荷数据分布。

由图2、3可知，同一个挡位段在3、4月中对应的室内室外温度范围都不同，且4月对应的室内温度略高于3月，4月对应的室外温度约比3月高1℃。由图可知，新风系统负荷与室外温度、室内温度相关。因此通信基站新风系统负荷预测模型的输入因子应考虑室外温度和室内温度。

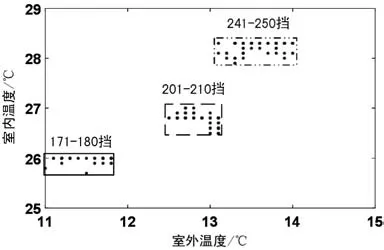
图2 3月负荷数据分布

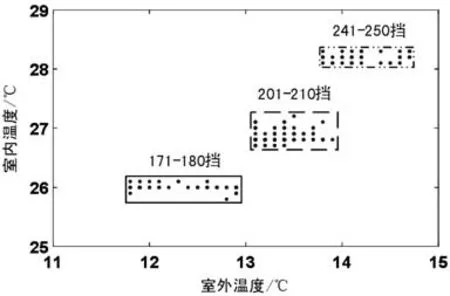
图3 4月负荷数据分布

1.3 输入因子关联性分析

输入因子的确立需要判断其对研究对象有无影响，影响或大或小的问题。而灰色关联分析法，是根据因素之间发展趋势的相似或相异程度，即“灰色关联度”，作为衡量因素间关联程度的一种方法[8]。

由基站数据分析可知，输入因子应考虑室外温度和室内温度。此外，基站数据中的新风系统负荷和通信基站空气湿度也需进行验证。基站数据中各影响因子与T+1时刻新风系统负荷的灰色关联度如表1所示。其中，T时刻室外温度、T时刻室内温度、T时刻空气湿度、T时刻新风系统负荷和T+1时刻新风系统负荷分别由W(t)、N(t)、S(t)、P(t)和P(t+1)表示。

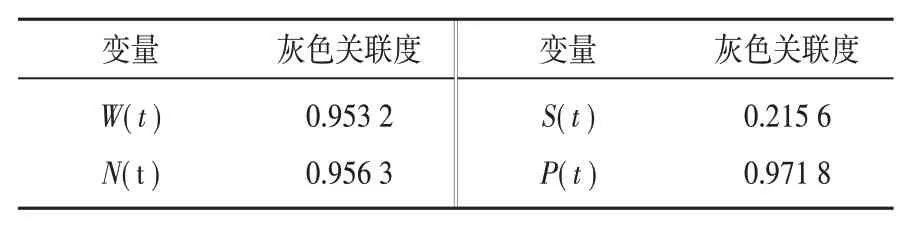
表1 各影响因子与P(t+1)灰色关联度

由上述分析可知，T+1时刻新风系统负荷与T时刻空气湿度关联度较小，关联度系数仅为0.215 6，这是因为该通信基站的空气湿度不由新风系统管理。而T时刻室外温度、T时刻室内温度、T时刻新风系统负荷与T+1时刻新风系统负荷的关联度大于0.95，因此选为新风系统负荷预测模型的输入因子。

2 通信基站新风系统负荷预测模型

2.1 构建负荷预测模型

基于GA-BP神经网络的通信基站新风系统负荷预测模型的建立主要分为以下3个步骤。

（1）确定负荷预测模型的输入因子及输出。由输入因子关联性分析可知其输入因子为T时刻室外温度、T时刻室内温度、T时刻新风系统负荷，输出为T+1时刻新风系统负荷。

（2）获取通信基站的原始数据并进行预处理，建立新风系统样本数据库。分别建立3、4月对应的新风系统样本数据库，选取其中部分样本数据如表2、3所示。

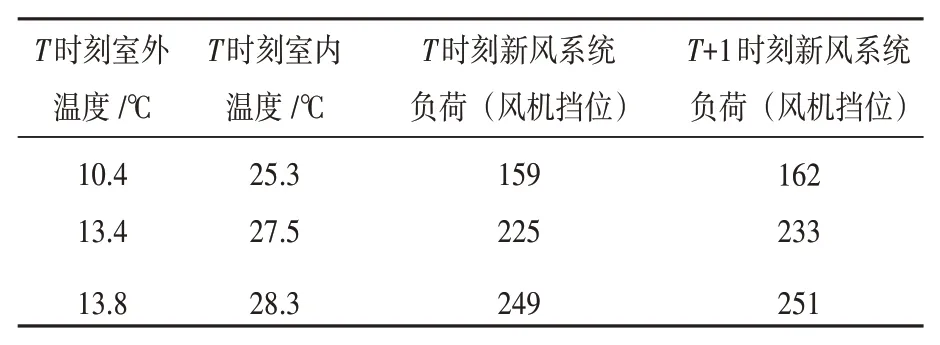
表2 3月样本库部分样本数据

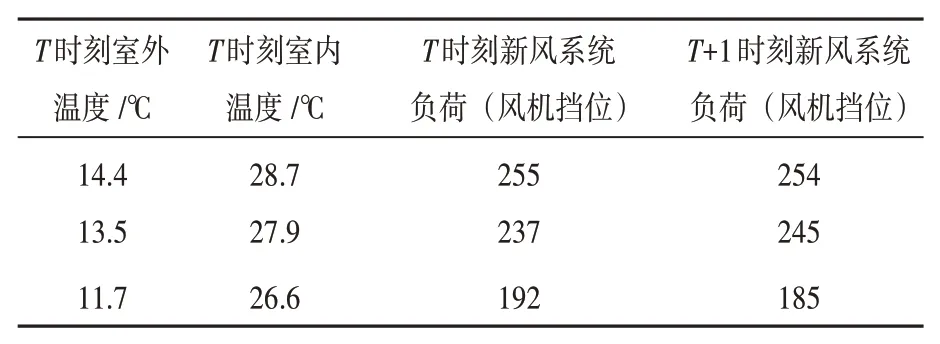
表3 4月样本库部分样本数据

（3）训练和测试样本的划分以及模型训练。分别对3、4月新风系统样本库进行样本划分与模型训练，图4所示为该负荷预测模型的神经网络结构图。其中，Atj（t=1，2，…，n；j=1，2，…，n）为该负荷预测模型中输入层和隐含层之间的权重系数，z t为隐含层的输入值，该层的输出值为at，Bt为该负荷预测模型中隐含层和输出层之间的权重系数。

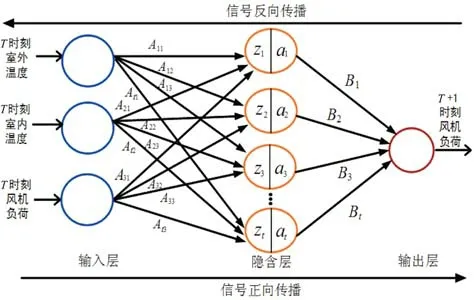
图4 神经网络结构

由于BP神经网络的初始权重及阈值的随机性，因此可能会陷入局部最小值[9]。利用遗传算法改进BP神经网络模型，通过GA模拟自然选择过程，并通过遗传理论对BP神经网络生成的初始解进行繁衍迭代，生成全局最优解。将最优的初始值输入BP神经网络模型进行数据训练，以生成最合理的基于GA-BP神经网络的新风系统负荷预测模型，以期得到最佳的预测值。

GA主要是优化BP神经网络的初始权值和阈值，先通过选择、交叉和变异等相关操作来获取最优数据[10-12]，再对其进行训练，最终输出新风系统负荷预测模型的最优结果。该负荷预测流程如图5所示。

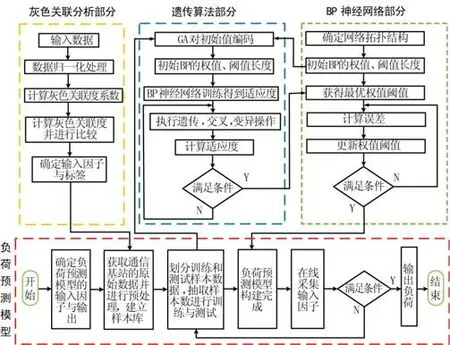
图5 负荷预测流程

2.2 负荷预测模型的参数选取

隐含层节点数的选定十分灵活，会直接影响负荷预测模型的预测精度。为了建立性能较佳的负荷预测模型，需确定隐含层节点数。负荷预测模型的输入因子和输出因子个数分别为3、1。隐含层节点数由经验公式（1）可计算得出：

式中：x为隐含层节点数；a为输入层节点数；b为输出层节点数；c为1～10的常数。

因此隐含层节点数可选择范围为3～12。隐含层节点数的选择可通过均方误差来判断，不同隐含层节点数的均方误差如图6所示。由图可知，当隐含层节点数为9个时，均方误差最低，因此最优隐含层节点数为9。其他参数选取如表4所示。

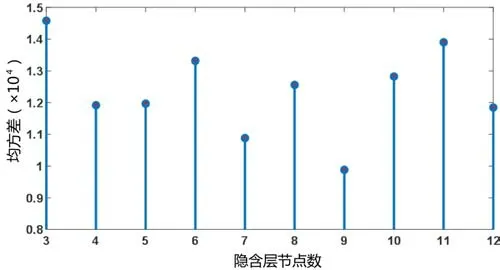
图6 不同隐含层节点数的均方误差

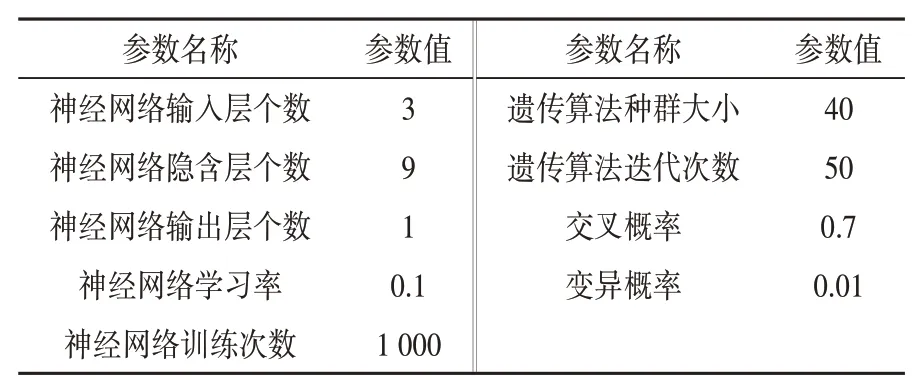
表4 模型参数表

3 预测结果与分析

实验分别以该通信基站3月和4月对应的新风系统样本数据库中70%的新风系统负荷数据、室外温度数据和室内温度数据作为训练集。以剩余的30%数据作为测试集对模型进行验证分析。

为了验证本文所提模型的可行性与有效性，将基于BP神经网络的预测模型和基于GA-BP神经网络的预测模型进行对比分析。随机选取3、4月份测试集中30个测试样本进行验证分析，3月份的两种模型的部分预测结果对比如图7所示，4月份的两种模型的部分预测结果对比如图8所示。

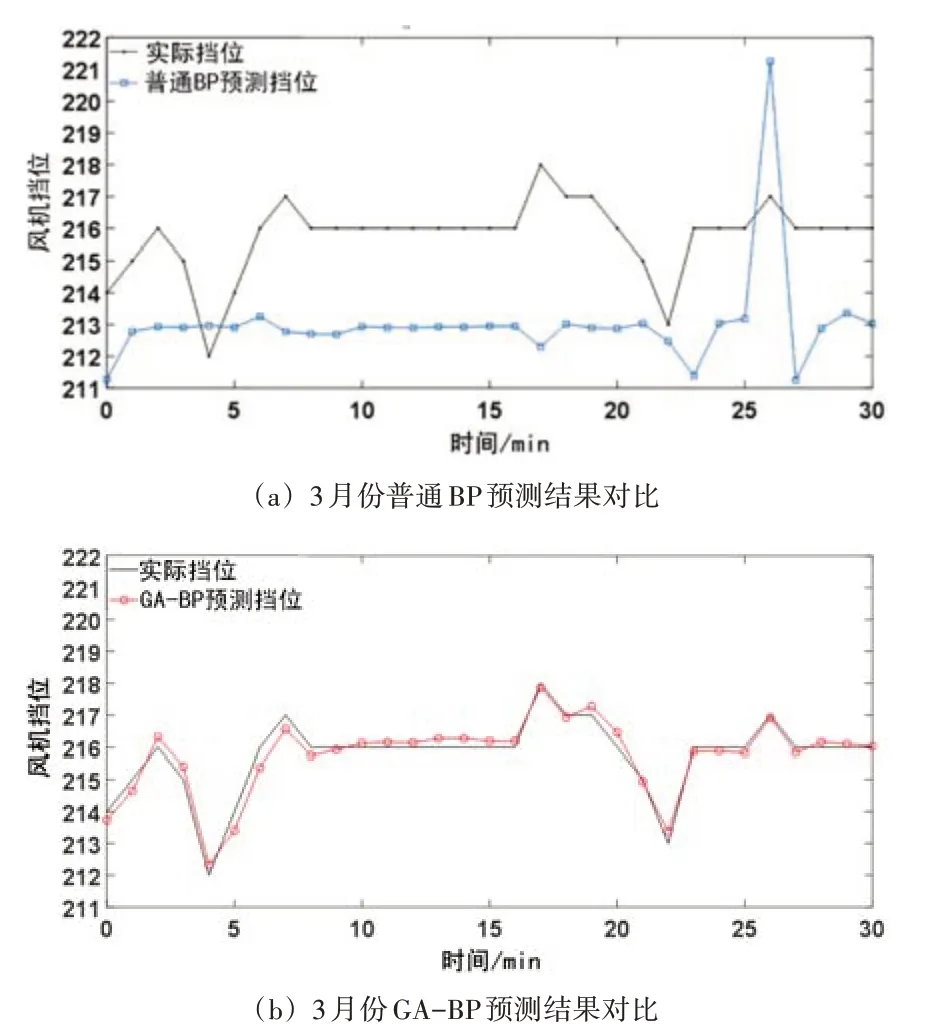
图7 3月份部分预测结果对比

图8 4月份部分预测结果对比

由随机选取的连续30个数据分析可知，BP神经网络预测值波动较大且与实际挡位相差较大。而GA-BP神经网络预测值与实际挡位相差较小。

为进一步得出两种预测模型误差对比，表5和表6分别给出了3月所有测试集的和4月所有测试集的对应的两种模型的平均相对误差。相对误差函数可表示为：

式中：为预测值；y为实际值。

由表5、表6可知，GA-BP预测模型的平均相对误差小于BP预测模型，其负荷预测准确率更高。其中，GA-BP预测模型的3、4月平均相对误差分别比BP预测模型降低了1.68%、1.67%。

表5 3月份相对误差分析

表6 4月份相对误差分析

4 结束语

为了降低通信基站新风系统的散热能耗，本文利用灰色关联分析法对通信基站新风系统中3月和4月的运行数据进行分析，确定了新风负荷的影响因素。根据影响因素建立了两个月对应的样本数据库，利用样本数据库中的训练集对BP神经网络进行训练，再利用遗传算法优化其参数，最终建立了通信基站新风系统负荷预测模型。模型建立后利用每个月对应的测试集分别进行验证，验证结果表明该负荷预测模型能满足工程实际需求，辅助基站新风系统实现节能运行，对通信基站新风系统的节能优化运行管理有着重要的应用价值。