基于LQR 的防摇控制系统设计
鲁 可, 陈思雅, 罗金格
(河南工业大学 电气工程学院, 河南 郑州 450000)
0 引言
随着工业生产的不断扩大,自动化程度的不断提高,吊车在现代化生产过程中应用越来越广, 港口吊车在港口物流中又起到意义非凡的效果。因此,研究怎样提高港口吊车的工作效率就显得尤为重要。 上海振华港机的超巴拿马岸边集装箱起重机小车速度达到244m/min。 小车的高速运行使得在消除集装箱摆动和迅速正确定位这一环节上花费的时间越来越多, 极大地影响了生产效率和装卸速度,并给安全生产带来隐患[1]。据试验,当小车运行速度达180m/min 以上、摆长为10m 时。小车制动后吊具及吊重物的摆幅可达2m,要经过约30s 摆动才停止[2]。
从上世纪50 年代起, 国外就开始了起重机防摆技术的研究。 最初是从输入整形控制开始, 输入整形控制是一种研究开发较早的开环控制技术,它最早由Smith 、Calvert提出,通过时滞滤波器(TDFTime-Delay Filter)对控制信号整形,消除了起重机吊重引起的残余振荡[3]。
港口的位置特殊, 起吊设备在工作时被起吊重物具有惯性力的影响,经常会出现左右摇摆现象。 因此需要为整个系统设计一个防摇摆控制器, 通过自动控制的方法消除起吊设备吊臂的摇摆。
本文对集装箱起重设备中的小车自动运行及负载防摇问题进行研究, 首先通过拉格朗日方程建立小车负载系统的动态模型,得出小车与负载摆动的运动规律,在此基础上,实际开发搭建防摇控制系统,实现小车防摇控制功能。
1 总体设计
本文对集装箱起重设备中的小车自动运行及负载防摇问题进行研究, 首先通过拉格朗日方程建立小车负载系统的动态模型,得出小车与负载摆动的运动规律,在此基础上,实际开发搭建防摇控制系统,并编程实现小车防摇手动和自动控制功能。桥机的实际系统存在复杂、非线性、时变、不确定、不完全等特点,还受小车与导轨的摩擦、风力的影响等干扰。 为了分析其本质,首先对起重机系统进行简化处理[4]。 总体方案设计见图1。

图1 总体方案设计图
防摇控制系统可以有手动和自动两种不同的控制方式; 手动控制方式中主要依靠司机师傅的经验随时调控电动机的转速来实现防摇控制,在此不予考虑;自动控制方案中限位开关确定防摇小车运行范围,角度传感器实时反馈摆臂与垂直方向之间的夹角,在装备初始化之后,在控制界面输入目标地址, 算法根据不同运行距离计算得到在整个运行过程中不同时刻的速度,将速度转化为电机的转速赋给电动机, 以实现在此过程中在角度累计最小的情况下实现时间最短且能精准停车的控制要求。 系统流程图见图2。

图2 系统流程图
2 硬件设计
防摇模型是由贝加莱工业自动化有限公司设计的, 用于实现防摇控制、倒立摆等功能的设备。 它主要由同步电机,直线导轨,摆锤三部分组成, 通过电机带动小车在导轨上移动,实现对摆锤的运动控制。
该防摇模型分为两个部分:正面是机械与电机部分, 背面是电气部分。 整个装置安装固定在特制电气柜中,电气柜为铝制框架全透明结构,设有安全门装置。
2.1 防摇系统模型
该防摇模型使用贝加莱ACOPOS 伺服驱动器控制贝加莱步进电机, 通过履带带动小车在直线导轨上移动。 小车单摆上装有编码器,用来检测摆锤位置。 装置正面的控制面板可以方便地实现小车运动控制。防摇系统装置见图3。

图3 系统装置图
2.2 主电路设计
主电路是指在电器设备或电力系统中,直接承担电能的交换的电路, 为整个系统以及大功率在执行元件提供动力,大多为220V 等高电压电路。 系统主电路见图4,控制电路见图5。

图4 主电路图

图5 控制电路图
3 软件设计
实际防摇系统比较复杂,除了元件的非线性外,还会受到各种干扰,如小车与导轨的干摩擦,外界风力的影响等等。 为了分析其本质,必须对吊车系统做简化处理,因此给出如下假设:①对于桥式吊车,由于吊车在进行装卸作业时,负载货物在竖直方向会有升降运动,本文只考虑小车的防摇特性,所以不考虑质量块在竖直方向的运动;②钢丝绳的质量相对于所吊负载的质量可以忽略不计;③钢丝绳的刚度足够大,其长度变化可以忽略不计,看成刚性绳;④吊物只在过导轨所在直线,垂直于水平面的竖直平面内运动;⑤不计风力影响和空气阻尼等。
通过上面的假设,吊车系统的力学简化模型见图6。

图6 吊车系统简化模型
其中:f1—为小车驱动力;f2—为摆锤拉力;x—为小车位移;θ—为小车位移;l—为摆锤长度;M—为小车质量;mg—为吊重重量;(x,y)—为重物的重心坐标。
建立平面直角坐标系,提取系统输入、输出状态变量,并建立其动力学关系,已知吊车M 当前位移为x,摆锤m 摆角为θ,摆 长 为l,根 据坐标定义可得:


LQR (Linear Quadratic Regulator)即线性二次型调节器, 其对象是现代控制理论中以状态空间形式给出的线性系统, 而目标函数为对象状态和控制输入的二次型函数,LQR 最优设计是指: 设计出的状态反馈控制器K 要使二次型目标函数J 取最小值。而K 由权矩阵Q 与R 唯一确定, 故此Q、R 的选择尤为重要,Matlab 的应用为LQR 理论仿真提供了条件,为实现稳、准、快的控制目标提供了方便, 二次型最优控制方法的优点是能够提供一套系统的方法,来计算状态反馈控制增益矩阵,LQR 控制器以最优控制计算得到的为参考量,求得控制变量1,使得角度始终处于可控范围内。
首先判断系统的可控性,由上述系统可得


4 系统调试
4.1 仿真调试
(1)无控制。 在没有控制的工程中角度随时间变化角度逐渐减小,见图7;若等待摆臂自身停止摆动这将是一个很漫长的过程。
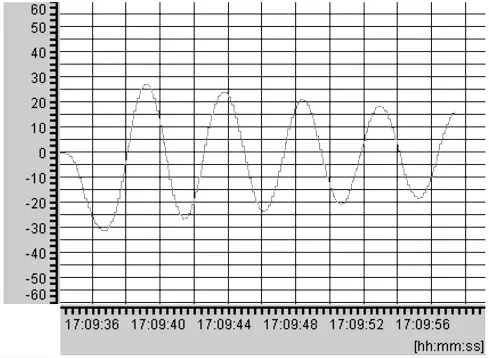
图7 无控制角度变化
(2)加入控制。系统初始化,加入控制算法得到角度变化图见图8。

图8 角度变化图
4.2 实物调试
将程序下载到PCC 中,在仿真系统中小车与摆锤的参数与实物的各项参数差别较小, 因此程序下载到控制器并进行参数调整便进行防摇控制,经过多次调试, 从众多调试结果中筛选出如下角度最小, 时间较短的实验结果trace 效果图见图9。

图9 Trace 图像
从图中可以得到如表1 数据:

表1 系统调试结果
此结果较好的完成了控制要求:实现准确停车,运动过程中摆角得累积和最小等控制要求。
5 结论
本文对集装箱起重设备中的小车自动运行及负载防摇问题进行研究,首先通过拉格朗日方程建立小车负载系统的动态模型, 得出小车与负载摆动的运动规律,在此基础上,实际开发搭建防摇控制模型,做到了定位准确和运动过程中摆角得累积和最小且时间短,成功将该模型应用在岸桥和轮胎吊设备中,具有良好的经济和社会效益。

