用于飞机模型参数辨识的飞行数据处理方法研究
叶子豪,张晓敏,刘亚飞,董朝阳
1.北京航空航天大学,北京 100191
2.中国飞行试验研究院航空工业飞行仿真航空科技重点实验室,陕西 西安 710089
随着航空技术的不断进步,机载传感器的数量大量增加,机载传感器所收集、交换的数据量成倍增长,飞行过程中产生的飞行器监测数据规模也随之不断增大。上述监测数据中包含了飞行器的全部状态量、控制量以及飞行轨迹等信息,能够充分体现当前飞行器控制系统设计的优劣,对控制系统的设计优化与飞行器性能的优化有着重要的指导意义。但现代飞行器的工作环境的复杂性与多变性将导致传感器采集到的数据中包含较多的异常数据,其中的野值、随机误差、零位误差、比例误差与时间延迟[1-2]是影响数据质量的重要因素,将对后续研究的过程与结果产生直接影响。
现有的多路传感器数据处理方法主要面向电气工程与雷达网络,面向飞行数据的误差辨识与补偿方法的研究较少,且存在过程不连贯、进行大规模数据处理时效率较低与通用性较差的缺点,难以满足飞行器监测数据的大规模特性的要求,在飞行数据的批量与快速处理上存在着较大不足,难以满足以飞行器控制系统的评估、设计与优化为目的的飞行器模型参数辨识以及后续多传感器信息[3]融合的需求。
关于以数据中时间延迟的辨识与补偿为代表的飞行数据处理方法,许多学者展开了研究。罗艺[4]等提出了基于极大似然法的异类传感器数据配准方法。Zhang Pixu等[5]基于最小二乘法提出了多平台传感器系统误差的配准算法。蔡金狮等[1]构建了考虑误差的飞行数据数学模型,并系统地总结了飞行数据相容性检验的基本方法。刘超等[6]利用同一来源的数据中不同测量量间的微积分关系对不同测量量间的时间延迟进行了计算与修正。同时结合基于真实试飞数据的气动导数辨识,验证了该方法的有效性。王伟[7]基于拉格朗日插值法和卡尔曼滤波法提出了一种改进型的数据时间配准方法。李富刚等[8]基于增广卡尔曼滤波法与输出误差法提出了一种新的飞行数据相容性检验方法。Panuntun等[9]提出了基于Smith预测器对四旋翼飞行器控制系统中的时间延迟的补偿方法,并结合仿真结果得出了该方法在跟踪性与抗干扰性方面的优势。唐思圆[10]等采用了遗传算法计算多传感器系统误差配准问题的解,并结合雷达真实数据与仿真数据验证了该方法的有效性。在基于飞行数据处理的飞行器模型参数辨识方面,段伟伟[11]等分析了神经网络、遗传算法在控制系统参数辨识与建模上的应用。
首先,本文基于纵向小扰动线性模型构建了离散化数据相容性检验模型,并使用该模型生成含异常数据的模拟飞行数据。其次,对数据中的野值展开了识别-剔除与补正,并基于Savitzky-Golay 法进行了数据的平滑滤波。再次,基于极大似然法设计了数据中时间延迟、零位与比例误差的辨识与补偿方法。结合应用实例表明,控制量数据的常值误差辨识与补偿显著改善了飞机模型参数辨识的迭代过程与结果的精度。最后,本文基于上述内容对结合常值误差补偿的飞行器模型参数辨识组合方法及其在飞行器设计中的应用进行了设计。
1 用于模型参数辨识的飞行数据处理方法
1.1 飞行数据相容性检验主要内容和方法
飞行器动力学系统试验的测量数据常含有零位误差或时间延迟等常值误差造成各实测数据互不协调,即各状态参数不满足运动方程组[1]。飞行数据不相容将对包括飞机模型参数辨识在内的后续数据挖掘与研究工作造成不利影响。本文结合飞行器纵向小扰动线性模型,对飞行数据进行相容性检验。飞行数据相容性检验的基本思路是,以飞行器动力学方程组作为状态方程,将常值误差与比例误差作为待估计参数,通过系统辨识方法估计出实测数据中的常值误差与比例误差并加以补偿,即可得到相容的飞行数据[1]。只有当某观测量既可以通过直接测量,又可以由其他观测量通过运动关系式求出时,即该观测量有多余的测量时,数据相容性检验才能够进行。用于估计零位误差、时间延迟与比例误差的飞行数据数学模型为
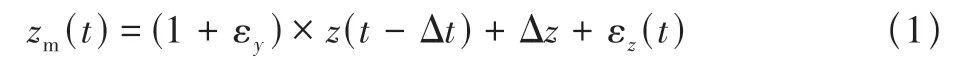
式中:zm为飞行数据实测值;z为飞行数据理想测量值;Δt为时间延迟;εy为比例误差;Δz和εz是由传感器的零位漂移及工作不稳定而引入的零位误差与随机误差,随机误差εz为白噪声,其均值为0,其方差为R。飞行数据实际值的表达式为
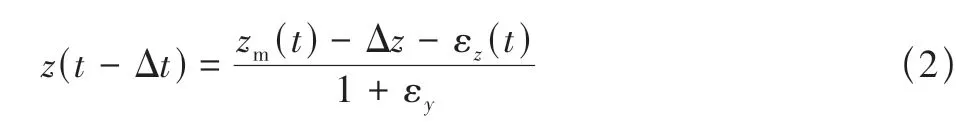
本文选用纵向小扰动线性模型作为状态方程,其矩阵形式为

状态变量x=[ΔV,Δα,Δq,Δθ]T,其中ΔV为速度变化值,Δα为迎角变化值,Δq为俯仰角速度,Δθ为俯仰角变化值。控制变量u=[Δδe,Δδp]T,其中Δδe为升降舵偏角,Δδp为油门大小变化。
系统矩阵A与控制矩阵B内的各项参数为在实际工程应用中为需要通过辨识得到的飞行器模型参数,通常为常数。纵向输出方程为y=Cx+Du,其中C为四阶单位矩阵,D为零矩阵。
结合飞行数据相容性检验的基本方程与选用的状态方程,建立含有零位误差、时间延迟、比例误差与随机误差的飞行数据相容性检验模型。其状态方程为
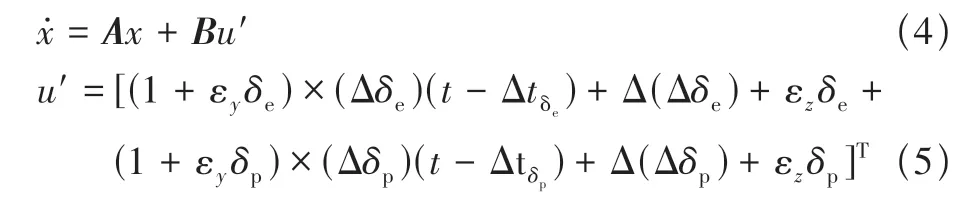
式中:[(Δδe)(t-Δtδe), (Δδp)(t-Δtδp)]为含时间延迟[Δtδe, Δtδp](以状态量的时间坐标为基准坐标)的控制量测量值;[Δ(Δδe),Δ(Δδp)]、[εzδe,εzδp]与[εyδe,εyδp]分别为控制量的零位误差、随机误差与比例误差。观测方程为

其中,xt=[ΔVt,Δαt,Δqt,Δθt],εzy=[εV,εα,εq,εθ],分别为状态量的测量值和随机误差。待估计的常值误差与比例误差为

可将上述方程表示的方程改写成以下形式

式中:控制量um=[(Δδe)t,(Δδp)t],状态量ym=[ΔVm,Δαm,Δqm,Δθm];θ为控制量的常值误差与比例误差;εzu和εzy分别为控制量和状态量的随机误差,其均值均为0,其协方差分别为Q和R。在此基础上,采用四阶龙格库塔法得到式(8)的离散化形式

本文通过所构建的基于纵向小扰动线性模型的离散化系统方程进行仿真飞行试验,以生成后续研究中所需的含异常数据的模拟飞行数据。首先将纵向小扰动线性模型参数以矩阵内元素的形式进行设定,并对输入变量与输出变量中的ΔV项进行无量纲化处理,设定模型参数值为

设置飞行数据采样组数为500 组,飞行数据采样频率为20次/s。采用飞行试验的典型动作“3211”信号[12]作为控制量数据,进行仿真飞行试验,获得后续研究中所需的含异常数据的模拟飞行数据。
1.2 野值的识别、剔除与补正
飞行数据中,野值的存在将降低试验结果与基于它得到的辨识结果的可信度与精度。因此需要建立正确的准则,剔除真正的野值并加以补正[1]。本文通过低阶多项式滑动拟合求得某点的期望值,测量值与期望值之差大于格鲁布斯阈值时将该点识别为野值,采用七点二阶多项前推差分算式[1]
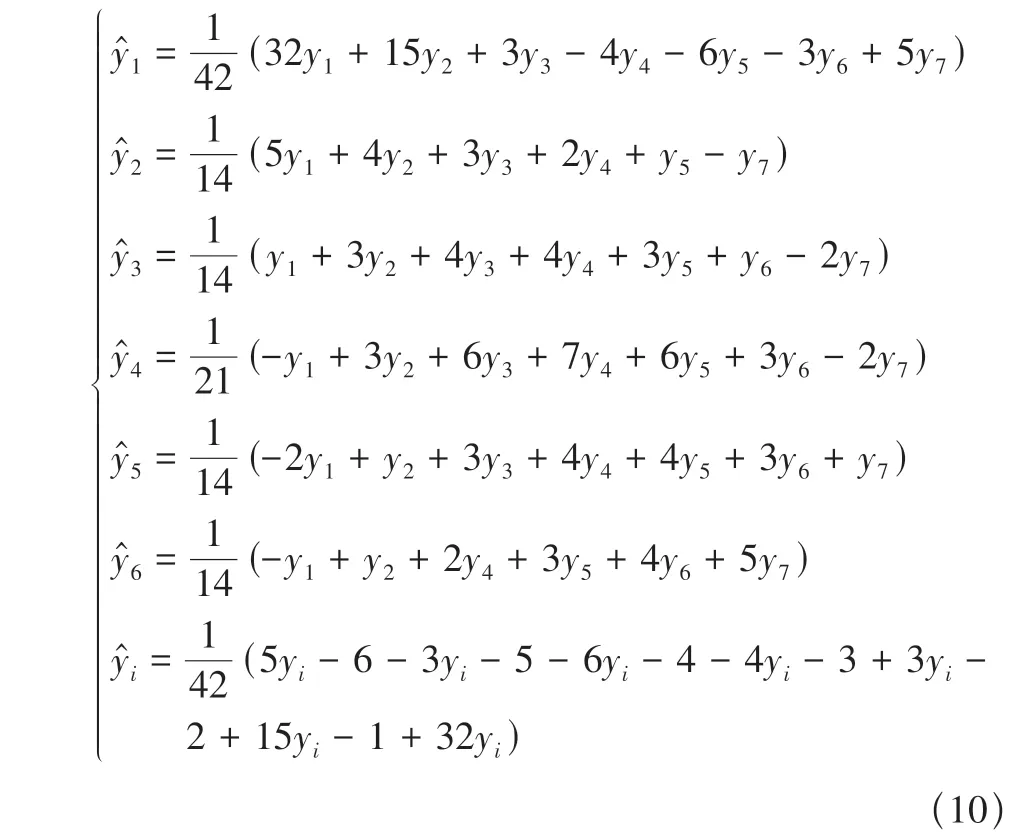
式中:i=7,8,9,…,N;yi与ŷi分别为第i点的测量值与期望值。按数据顺序逐点计算期望值ŷi及新息vi=yi-ŷi。取置信度α=99%,由格鲁布斯临界值表可知K(7,0.99)=2.097,满足式(11)的点可视作野值点
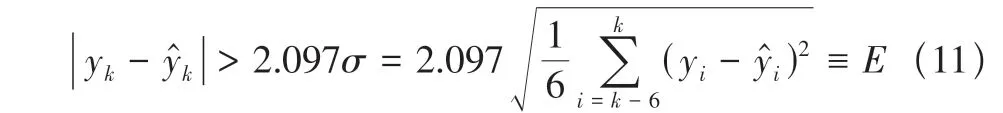
数据中可能出现较为接近的连续跳点,当k点为野值时,满足式|yk+i-yk|<E的点也为野值[1]。为避免将阶跃信号误识别为野值并将其剔除的情况发生,取m=3,当式(11)满足k+i>k+3时,可以认为yk,yk+1,…,yk+m都为正常值[1]。在识别出已判定为野值的点并加以剔除后,采用以野值点前三点yk-3,yk-2,yk-1和后三点yk+m+1,yk+m+2,yk+m+3为已知值的六点拉格朗日插值进行野值点的补正[1]

式中:满足i,j≠k,k+1,…,k+m;i≠j;l=k,k+1,…,k+m。y͂k,y͂k+1,…,y͂k+m为各野值点补正值。野值处理方法在模拟飞行数据上的应用实例如图1所示,其中黑色、绿色圆圈分别代表识别出的野值点与野值补正点。

图1 野值的识别、剔除与补正Fig.1 Identification,elimination and correction of outliers
由图1 可以看出,野值补正点相较于识别出的野值点更贴合预测值曲线。该方法对飞行数据中的孤立野值点与连续跳点均具有较好的补正效果。
1.3 数据的平滑滤波
受机身振动、电磁干扰等因素影响,数据常含有测量噪声,其使得计算残差增大,从而导致气动参数辨识过程难以收敛或辨识结果错误,因此必须滤除数据中的测量噪声[8]。本文利用Savitzky-Golay法对数据进行平滑滤波。
Savitzky-Golay法的核心思想是对一定长度窗口内的数据点进行k阶多项式拟合,用拟合值代替原始数值,从而实现高频噪声点的去除与原始数据序列的平滑[13]。对离散化数据而言,该方法实际上是一种移动窗口的加权平均算法,但是其加权系数是通过在滑动窗口内对给定高阶多项式的最小二乘拟合得出[14]。将1.1节中生成的含异常数据的模拟飞行数据导入该方法,得到平滑滤波效果如图2所示。

图2 基于Savitzky-Golay法的数据的平滑滤波Fig.2 Smoothing filtering of data based on Savitzky-Golay method
由图2 可以看出,Savitzky-Golay 法在飞行数据的平滑滤波中能够在较好保持数据细节信息的同时滤除数据中的随机误差,能够满足飞行数据预处理的要求。
1.4 常值误差与比例误差的辨识与补偿
本文数据中的零位误差、时间延迟与比例误差对状态量的影响方式已在上文的离散化飞行数据相容性检验模型中得到确定,此时需要通过特定准则,将参数估计问题等价替换为求准则函数极值的问题,从而辨识出数据中的零位误差、时间延迟与比例误差。本文利用极大似然法进行数据中常值与比例误差的辨识。对于给定的一组与待辨识参数θ有关的观测量Z,极大似然法参数辨识的实质是通过不断迭代,寻找使得选定的似然函数L取得极大值的参数θ̂。当似然函数取为条件概率p(Z|θ)时,极大似然参数估计就是寻找使Z出现的条件概率达到极大值时对应的θ̂[15]。通过基于观测数据的统计学性质与假设的一系列化简与转化,得到似然准则函数为
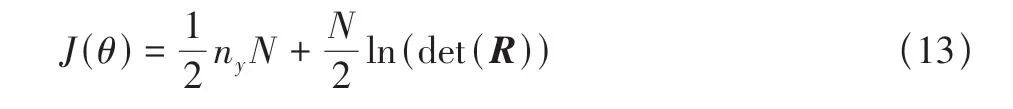
式中:ny为待辨识参数个数,N为观测数据组数,R为量测误差协方差矩阵,det(R)为矩阵R的行列式。此时,极大似然参数辨识可以转化为在离散化飞行数据相容性检验模型的约束下,通过不断迭代求得似然准则函数J(θ)取得极小值的θ̂[16]。其基本流程如图3所示。

图3 极大似然法流程Fig.3 Flow chart of maximum likelihood method
1.4.1 零位误差辨识与补偿算例
选取待估计参数θ=[Δ(Δδe),Δ(Δδp)],默认其他数据不含有零位误差。向控制量数据加入大小为[-0.3(°),4]的零位误差和方差均为10^(-2)的随机误差,并向状态量数据加入方差均为10^(-1)的随机误差。采用matlab 中求多元非线性函数最小值函数“fmincon”迭代得到θ的最优解。零位误差辨识值随迭代次数变化过程与辨识结果如图4与表1所示。
基于辨识值的控制量的零位误差补偿前后得到的状态量响应曲线对比如图5所示。
由图4、图5及表1可以看出,零位误差辨识值随迭代次数增加快速收敛至真值附近,且辨识结果具有较高精度。基于零位误差补偿后的控制量数据生成的状态量数据与无零位误差下的真实数据符合较好。
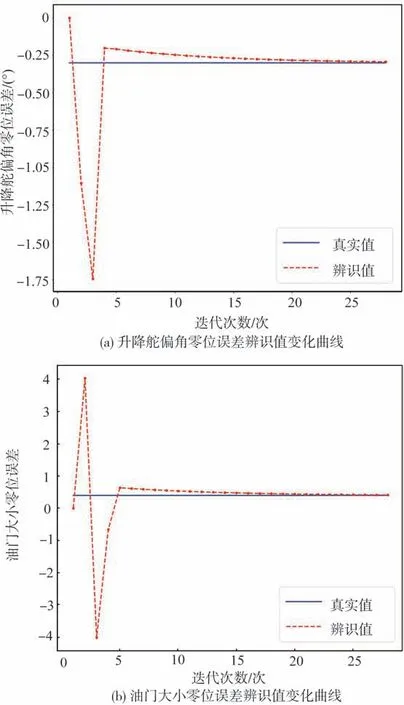
图4 零位误差辨识值随迭代次数变化曲线Fig.4 Variation curve of the identification value of zero error with iteration times

图5 零位误差补偿前后响应曲线对比Fig.5 Comparison between response curves before and after zero error compensation
1.4.2 时间延迟辨识与补偿算例
选取估计参数θ=[Δtδe,Δtδp],默认其他数据不含有时间延迟。向控制量数据加入[8,-6](单位:个采样周期,本文取0.05s)的时间延迟,并向状态量数据加入方差均为10^(-1)的随机误差。时延辨识值随迭代次数变化过程与辨识结果如图6和表2所示。
基于辨识值的控制量的时间延迟补偿前后得到的状态量响应曲线对比如图7所示。
由图6、图7 及表2 可以看出,时间延迟辨识值的收敛较慢,中间还存在一些阶梯状变化,最终还是收敛于真值附近,且辨识结果具有较高精度。基于时间延迟补偿后的控制量数据生成的状态量数据与无时间延迟下的真实数据符合较好。

图6 时间延迟辨识值随迭代次数变化曲线Fig.6 Variation curve of the identification value of time delay with iteration times
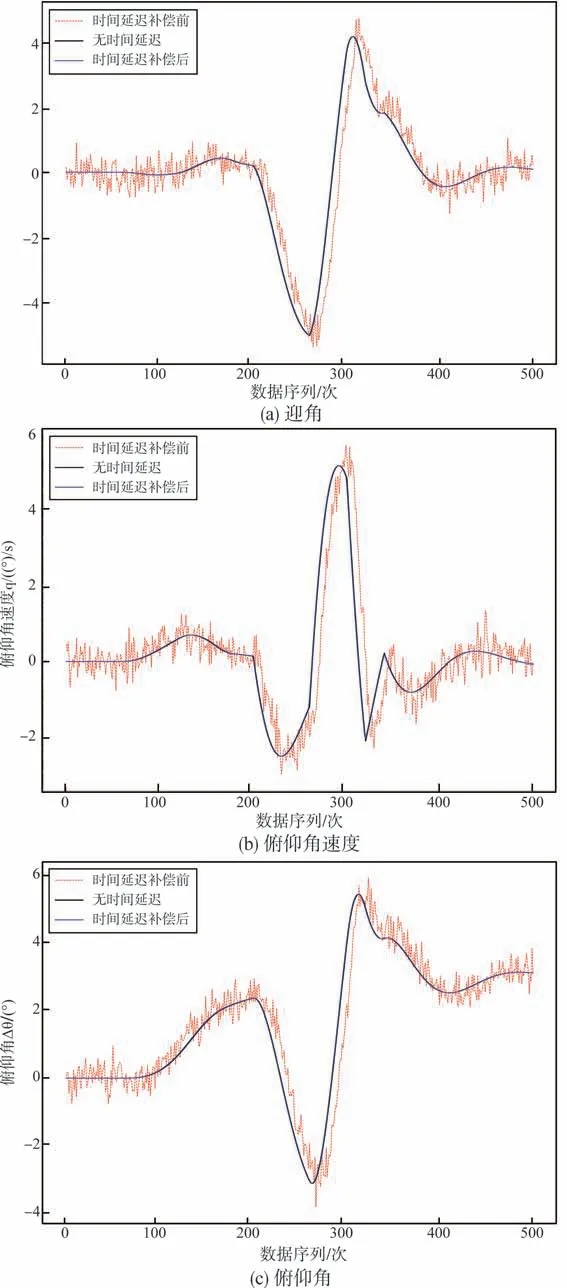
图7 时间延迟补偿前后响应曲线对比Fig.7 Comparison between response curves before and after time delay compensation

表2 时间延迟辨识结果Tabel 2 Identification result of time delay
1.4.3 比例误差辨识与补偿算例
选取待估计参数θ=[εyδe,εyδp],默认其他数据不含比例误差。向控制量数据加入大小为[0.6,-2.4]的比例误差,并向状态量数据加入方差均为10^(-1)的随机误差。
比例误差辨识值随迭代次数变化过程与辨识结果如图8 和表3 所示。基于辨识值的控制量的比例误差补偿前后得到的状态量响应曲线对比如图9所示。
由图8、图9及表3可以看出,比例误差辨识值随迭代次数增加迅速收敛至真值附近,且辨识结果精度较高。基于比例误差补偿后的控制量数据生成的状态量数据与无比例误差下的真实数据符合较好。

图8 比例误差辨识值随迭代次数变化曲线Fig.8 Variation curve of the identification value of proportional error with iteration times

图9 比例误差补偿前后响应曲线对比Fig.9 Comparison between response curves before and after proportional error compensation

表3 比例误差辨识结果Tabel 3 Identification result of proportional error
从上述算例中可以看出,本文提出的基于极大似然法的飞行数据处理方法可以较为快速精确地估计出各控制量数据相对于状态量数据的零位误差、时间延迟与比例误差的大小,且基于补偿后的控制量数据生成的状态量数据更为贴合无控制量误差下的真实状态量数据。
2 飞行数据处理方法在模型参数辨识中的应用
在基于飞行数据进行飞行器模型参数辨识的实际应用中,通常已知的数据包括状态量初值X0、通过理论计算或风洞试验的气动数据得到的气动参数预估值θ0、飞行试验中由传感器收集到的控制量数据U0与状态量观测数据Z。其中的原始控制量数据U0常常含有大小未知的时间延迟与零位误差,这可能给基于飞行数据的直接飞行器模型参数辨识造成不利影响,直接影响到飞行器的后续设计与优化工作。
基于此,本文围绕控制量的常值误差补偿前后的飞行器模型参数辨识过程与结果间的对比,对所提出的飞行数据处理方法在飞行器模型参数辨识中的应用进行了研究。设定待辨识参数真值为

采用上文仿真飞行试验中的仿真设置与模型、补偿前后的控制量与状态量数据,以上节内容中设定的纵向小扰动模型参数值作为待辨识参数初始值,基于极大似然法对模型参数进行辨识。
2.1 常值误差补偿前后控制量下的模型参数辨识结果
控制量的常值误差补偿前后,各待辨识模型参数(设定A、B矩阵中的参数A11、A12、A14、A21、A22、A31、A32、A33、B11、B21、B31,均为无量纲量)随迭代次数的变化曲线如图10 所示。其中黑色实线代表给定的待辨识参数真实值,红、蓝色虚线代表常值误差补偿前、后的模型参数辨识值变化曲线。
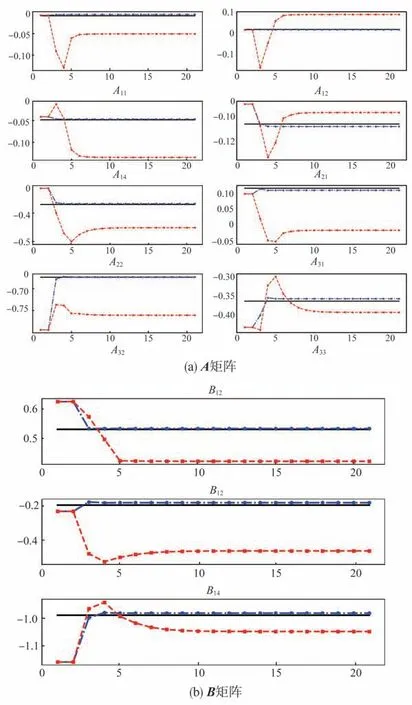
图10 模型参数辨识值随迭代次数变化曲线Fig.10 Variation curve of model parameter identification value with iteration times
由图10 及表4 可以看出,控制量的常值误差补偿后的参数辨识过程收敛较快,且辨识精度更高。长、短周期模态是飞行器纵向运动的固有特性,是分析飞行器的纵向动稳定性的重要依据。本文分别对基于给定真实的系统矩阵A参数与通过常值误差补偿前后模型参数辨识值得到的系统矩阵A的纵向模态特征值进行计算与对比。由表5可以看出,常值误差补偿后模型参数辨识值下的系统矩阵A的纵向模态特征值在不同模态上更为接近给定真实的纵向模态特征值。由图11可以看出,基于常值误差补偿后模型参数辨识值得到的状态量数据更为贴近基于给定真实模型参数辨识值得到的状态量数据。
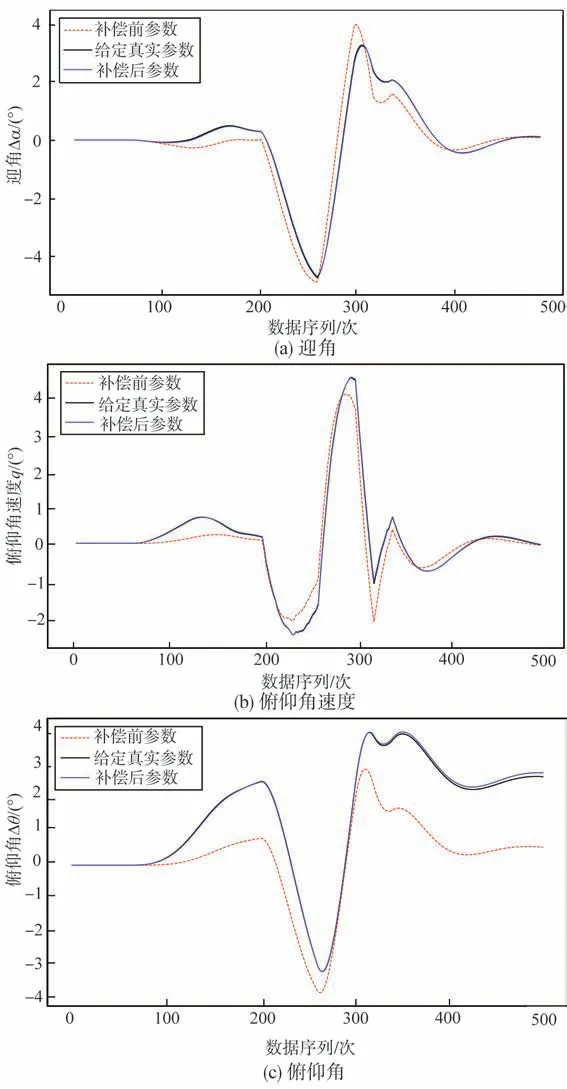
图11 常值误差补偿前后模型参数得到的响应曲线对比Fig.11 Comparison between response curves obtained from model parameters before and after constant error compensation

表4 常值误差补偿前后模型参数辨识结果Tabel 4 Model parameter identification result before and after constant error compensation

表5 补偿前后模型参数辨识结果的纵向模态对比Tabel 5 Longitudinal mode comparison of model parameter identification results before and compensation
2.2 结合常值误差补偿的模型参数辨识组合方法
在所设计的飞行数据处理方法及其在模型参数辨识中的应用的基础上,本文进一步提出了结合常值误差补偿的飞行器模型参数辨识组合方法。其基本思路是:通过基于模型参数初始值与状态量观测数据的控制量常值误差的辨识与补偿环节和控制量常值误差补偿后的模型参数辨识环节的不断迭代以及模型参数初始值的不断更新,逐渐缩小状态量计算数据Y与状态量真实观测数据Z之间的差异,从而使模型参数辨识值与控制量数据逐渐接近真实值。其流程如图12所示。
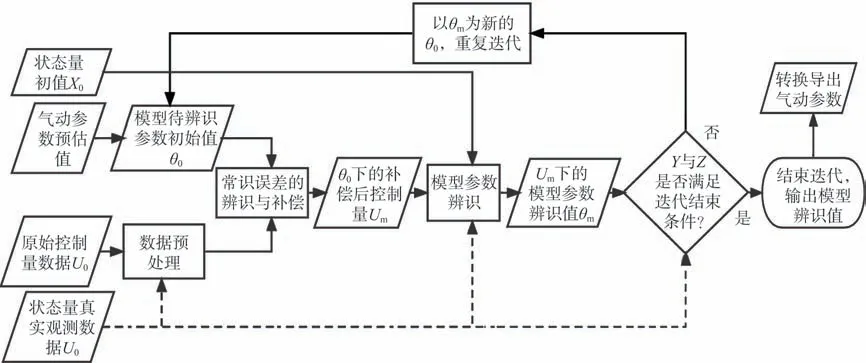
图12 结合常值误差补偿的参数辨识组合方法步骤Fig.12 Step diagram of the combination method of parameter identification combined with constant error compensation
3 结论
本文主要对飞行数据中异常数据的辨识与补偿方法及其在飞行器模型参数辨识中的应用进行了研究,提出了一套从数据中野值与随机误差的消除,到结合数据相容性检验的时间延迟、零位误差与比例误差的辨识与补偿的飞行数据处理方法,并结合模拟飞行数据中异常数据的辨识与补偿实例验证了本文所提方法的可行性。常值误差补偿前后的控制量数据下的模型参数辨识过程与结果之间的比较表明,本文提出方法中控制量数据的常值误差辨识与补偿能够显著改善飞行器模型参数辨识的迭代过程与结果的精度。基于上述内容,本文对结合常值误差补偿的飞行器模型参数辨识组合方法中的应用进行了设想。本文研究的内容对于进一步推动飞行器模型参数辨识在飞行器设计中的实际应用具有积极意义。后续研究将选用更多飞行器动力学模型与飞行数据种类构建数据相容性检验模型,以进一步拓宽本文所提方法的适用范围。

