基于改进RBF算法的建筑能效预测模型的构建①
王 坤
(淮南职业技术学院, 安徽 淮南 232001)
0 引 言
随着我国经济的快速发展,办公建筑的节能也逐渐受到社会各界的关注。近年来,我国的建筑能耗在全社会中的能耗占比越来越高[1]。其中,公共建筑的能耗强度最大,特别是一些单体面积较大的建筑,该类建筑通常采用了集中式中央空调,其能耗强度也是远超其他建筑[2]。虽然大型公共建筑的能耗巨大,但是利用率却非常低,约为30%[3]。因此,解决我国大型公共建筑的高能耗和低能效的问题,已经成为了相关领域研究的热点。大型公共建筑中的耗电设备较多,日均耗电量非常高,同时电力浪费现象也非常突出。以往由于技术上的限制,使得建筑用能长期处于一种粗放式管理状态[4]。随着科技的发展,智能电网技术逐渐开始被广泛应用,智能电网技术有效的指导了建筑节能方向,并使能源利用率进一步得到了提升[5]。因此,构建了基于改进径向基函数(RBF)算法的建筑能效预测模型,并选取某办公建筑2019年5月~2020年3月在工作日内的能耗数据,对提出的模型进行了验证,旨在为类似的研究课题提供一定的参考。
1 办公建筑能效预测模型构建
1.1 PSO-LM算法优化RBF神经网络
RBF是一种多变量插值的常规技术,而RBF神经网络的类型属于三层前向神经网络,其优点包括收敛效率高、拟合能力强、训练快速、学习能力强、网络结构简单等,同时还存在全局唯一最佳逼近的特征,在各大领域都具有重大的意义。RBF神经网络一共分为三层,分别为输入层、隐含层和输出层[6]。输入层将输入的变量传入由RBF构成的隐含层,变量在隐含层中进行非线性变换,再将隐含层中输出的变量导入输出层进行线性变换,以达到整体性输出[7]。若RBF神经网络输入层的节点为m,隐含层的节点为q,输出层的节点为l,其中,在隐含层中的作用函数,如式(1)-式(3)所示。
(1)
(2)
(3)
一般情况下,RBF函数均应用了的高斯函数,所以RBF神经网络的隐含层可以采用式(4)表示。
(4)
式(4)中,‖x-ci‖表示欧式范数;ci=[ci1,ci2,…,cim]T表示高斯函数中心向量;x=[x1,x2,…,xm]T表示输入向量;σi为基函数方差;ui表示隐节点i的输出,i=1,2,…,q。
RBF神经网络输出层采用线性变换的方式对输入信号进行处理,应用线性映射方法整体输出从隐含层中输入的数据,见式(5)。
(5)
式(5)中,θk为输出阀值;wki表示加权系数;yk为输出层的输出;k为节点数。在预测控制系统中应用RBF神经网络算法时,若系统模型已知,能够在RBF神经网络的基础上创建被控对象模型,被控对象可以直接应用在控制系统之中[8]。以辨识器的形式存在于控制系统之中,对模型参数未知和高度非线性的系统进行辨识,并将采集的样本数据用于样本训练,在系统模型的建立过程中,不必了解系统详细的内部结构;也能作为控制器使用,同时也能够对未来数据进行预测。
在粒子群(PSO)算法的D维目标搜索空间中,若粒子群由m个粒子组成,则不同粒子均对应着解决问题的一个可行解。通过迭代找到粒子的最优位置,第i个粒子的D维位置矢量表示为zi=(zi1,zi2,…,ziD),粒子飞行速度表示为vi=(vi1,vi2,…,viD),粒子迄今寻到的最优位置表示为pbesti=(pi1,zi2,…,pid,…,piD),整个粒子群迄今寻到的最优位置表示为gbesti=(gi1,gi2,…,gid,…,giD)。
(6)
(7)
式(6)为粒子速度的更新表达式,式(7)为粒子位置的更新表达式。其中k,W依次表示迭代次数、惯性权重;r1,r2为[0,1]间的随机数;c1指学习因子;c2指加速因子;通常情况下经验值取c1=c2=1。种群中粒子的当前位置可以表示为BP权值与阈值的集合,进行神经网络权重矩阵的扫描以及神经网络阈值的扫描,并进行粒子位置的初始化操作。
(8)
粒子可根据式(7),(8)更新位置和速度,进而完成迭代。
(9)
式(9)为粒子速度迭代的权重θ计算式,其中θmax表示初始权重,θmin表示最终权重,kmax表示最大迭代次数,k表示当前迭代次数。研究过程中利用PSO算法进行BP神经网络权值、阈值的学习训练,进而找出粒子群最优位置。
(10)
(11)
(12)
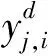
LM(Levenberg-Marquardt)算法属于一种能够对大规模参数进行优化的算法,是目前训练网络最有效的方法之一。采用了文献[9]中的LM算法来实现与PSO算法的结合。RBF神经网络参数的选择决定了预测模型的优劣,然而参数选择具有一定的随机性,无法确保模型的准确性。因此,引入了PSO-LM算法来帮助RBF神经网络进行参数选择[10-11]。采用PSO-LM优化后的RBF神经网络结构,如图1所示。
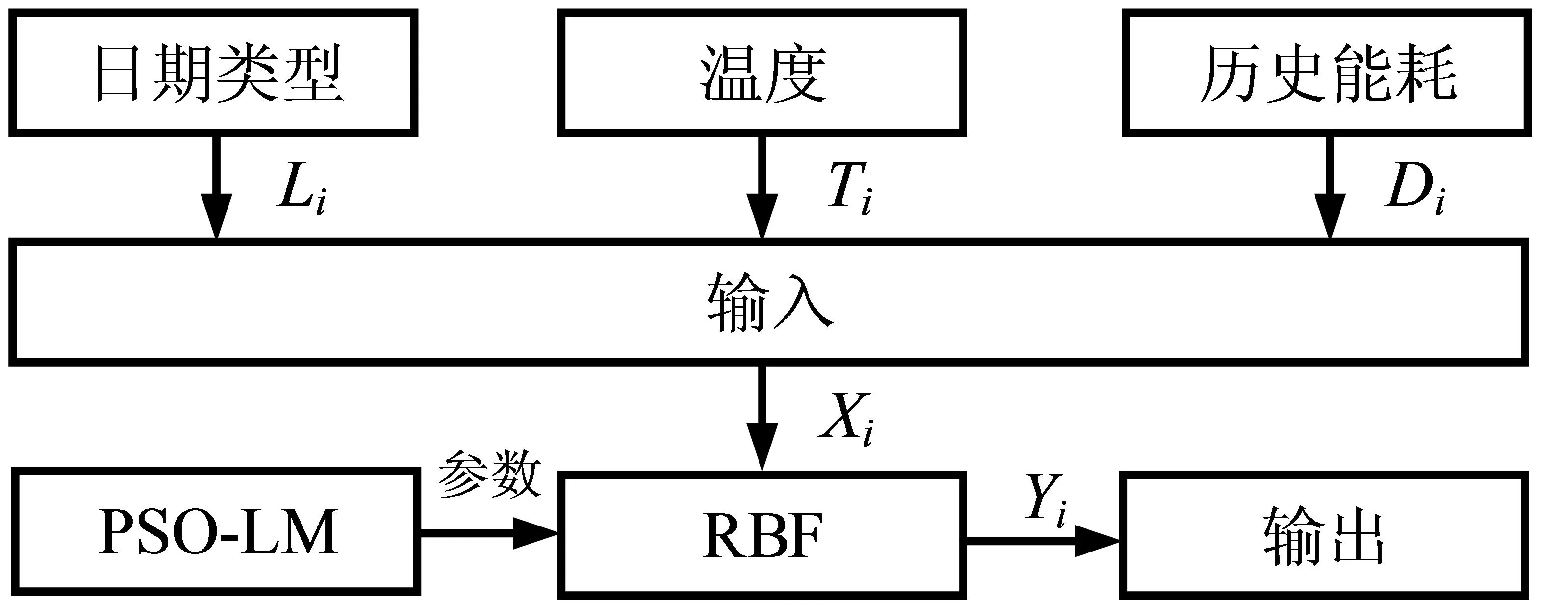
图1 PSO-LM优化后的RBF神经网络结构
1.2 基于PSO-LM-RBF神经网络的模型构建
建筑能效预测就是应用能够影响能耗的因素和以往的历史数据,并采用适当的方法进行未来用电量的预测。预测类别的区分主要为分、时、天、周、月、年等时间周期,其中分、时以内的预测为超短期负荷预测,天、周以内的预测为短期负荷预测,月、年以内的预测为中期负荷预测,年以上的预测为长期负荷预测[12]。采用短期负荷预测的方式对建筑能耗进行分析,通常短期负荷预测的基础数据量非常大,同时具有较强的连续性,变化特征明显。因此选用RBF神经网络对预测模型进行构建。
基于PSO-LM-RBF神经网络构建能耗预测模型的具体流程共有7步,如图2所示。第一步是选取建模需要的能耗数据,包括日期类型及气象数据等,形成初始数据样本集。第二步是进行初始数据的预处理操作。通常原始能耗数据存在少量缺失及异常的现象,必须进行预处理操作才能确保结果的准确性。采用文献[13]中的归一化处理方法对原始能耗数据进行处理。第三步是创建数据样本集。由于电力能耗一般为连续时间序列数据,可采用待预测时间点的前N个数值推测后面的M个数值,输入、输出数据分别为XK,XK+1,…,XN+K-1、XN+K,XN+K+1,…,XN+M+K-1,将能耗数据划分为K组,输入、输出分别为N,M,即数据的长度为输入输出之和。将样本数据的前一部分进行RBF神经网络训练,在此期间确定网络的参数,构建RN到RM的映射,采用样本的后一部分数据在训练后得到的模型中进行预测,分析预测结果和模型性能。第四步是对RBF的参数进行确定,采用聚类算法初始化RBF的网络参数,再应用PSO-LM算法对网络参数进行优化。第五步是采用样本数据训练网络,并对预测与期望的输出值之间的误差进行计算,直至精度符合实验要求。第六步选择网络输入为测试集,并得出[0,1]内的预测结果。第七步归一化处理全部测试结果,并计算出预测的能耗值xt,归一化公式为xt=x(xmax-xmin)+xmin,x为预测在[0.1]之间的结果,xmax,xmin为预测时间内的最高、最低能耗值。

图2 基于PSO-LM-RBF神经网络的能耗预测模型流程
基于PSO-LM-RBF神经网络的能耗预测模型具有实时性特征,可以采集建筑运行中的实时数据,并导入模型对今后的用电趋势进行预测。该模型还存在一定的通用性,可以发现各类建筑在各个时间的能耗,以实现对建筑未来用电情况的预测。
2 组合液压自爬模结构验算结果
2.1 样本数据处理及网络结构确定
选择某大型建筑2019年5月-2020年3月在工作日内的能耗数据,并且为了确保模型验证的准确性,将数据分为冬季和夏季两个阶段进行负荷预测,夏季选择5~8月的数据为训练集,9月为测试集;冬季选择11月-2月的数据为训练集,3月为测试集。对样本数据进行分析后发现,某天的能耗数据和前几天的数据均存在一定联系,可以在数据输入时,对连续7d的能耗数据进行预测。同时,当天的温度高低也一定程度影响着用电负荷。所以在对样本数据进行训练时,输入向量X可为10个特征向量,X=[x1,x2,...,x10]T,其中,x1表示之前1d内的最高温度数据,x2表示之前1d内的最低温度数据,x3表示日期数据类型,x4-x10表示之前一周同一时间的能够数据。对所有数据进行归一化处理,归一化后的数据能够确保模型预测的准确性,不会出现因个别因素而造成对结果较大的影响。
对于网络结构的确定,网格输入、输出维度分别为10维、1维。训练数据应用K-means方法进行聚类,以保证隐含层节点在任意指定下也能够达到达到预测的精度要求。采用聚类在3-19时的轮廓系数评价聚类效果,如图3所示。由图3可知,聚类效果最优时的聚类数为12个,那么选取隐含层中节点数目为12个进行模型验证,搭建的RBF神经网络结构为10-12-1。
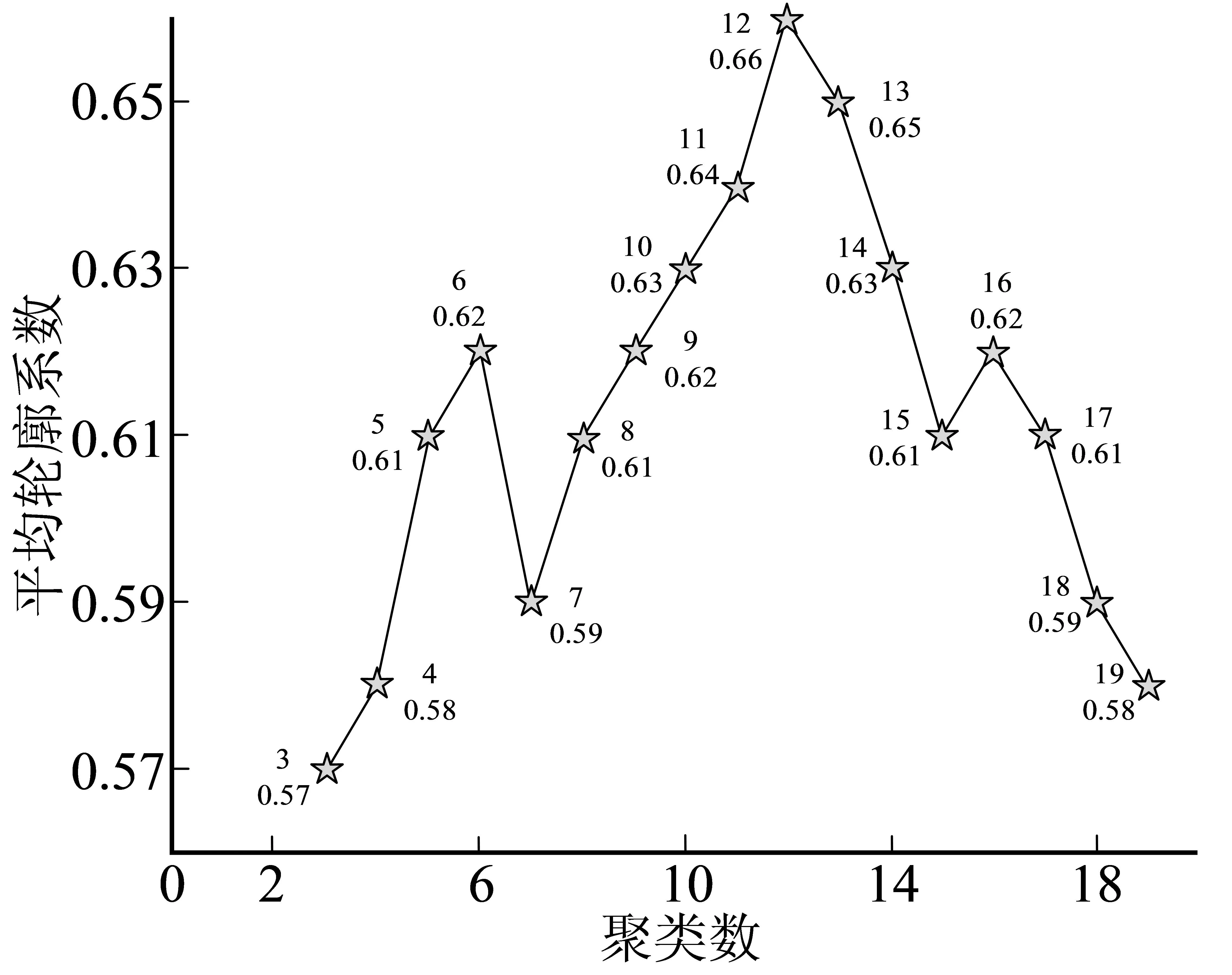
图3 聚类在3-19时的轮廓系数
2.2 模型仿真测试及分析
研究应用MATLAB测试改进前后模型的性能。改进后的PSO-LM-RBF模型参数设定为:LM的误差ε范围在10-6,系数β为10,阻尼因子μ0为0.001;确定PSO的粒子数m为40个,加速因子c1,c2均为2,惯性权重ω在0.4~0.9以内变化,迭代次数k为300次,误差范围在10-6,最大位置Xmax为10,最大速度vmax为10。仿真模型的目标精度设定在0.001,通过相同的数据进行模型训练,得到模型性的收敛性能,如图4所示。
图4 改进前后RBF神经网络收敛性对比
由图4可知,改进后的RBF神经网络的收敛速度显著高于改进之前,改进后的RBF神经网络仅需26个周期即可收敛,精度为0.00036,而改进前的算法需要352个周期才能收敛,精度为0.00098,改进后的RBF神经网络的收敛速度显著高于改进之前。
选择夏季和冬季两个阶段的数据来证明模型的准确性,并采用其中的训练集数据对参数进行训练,得到能够预测能耗的最终模型。在各阶段数据训练后的模型中导入影响因素和训练集数据,预测2019年9月和2020年3月的负荷数据。由于神经网络预测存在一定的误差,所以本研究在验证时分别进行了15次预测,并取最后的平均值为预测结果。见图5所示。
(a)夏季 (b)冬季
由图5可知,对夏季数据进行预测,改进后的PSO-LM-RBF神经网络模型的预测结果更接近实际的输出负荷值,RBF神经网络的预测误差较大;对冬季数据进行预测时,两种模型均能够较好的预测负荷的输出,但改进后的PSO-LM-RBF神经网络模型预测精度更高,更接近实际负荷输出。
进一步对两种模型的预测误差进行分析,主要是将预测值与实际值相对比,结果越相近则误差越小,模型的性能就越好。应用了平均相对误差对两种模型的误差进行计算[14]。改进前后的算法预测结果对应的相对误差,如图6所示。
(a)夏季 (b)冬季
由图6可知,PSO-LM-RBF神经网络模型的相对误差更低,预测结果相对稳定。为了能够更好的验证模型的预测性能,通过计算日最大误差百分比和平均相对误差百分比,对两种模型进行对比验证。结果如表1所示。

表1 对比模型预测误差结果
由表1可以看出,改进后的算法的相对误差低于2.3%,平均、最大相对误差均显著低于改进前。其中,夏季、冬季预测的最大相对误差分别下降了4.96%,3.67%;平均相对误差分别下降了2.19%,1.45%。该结果说明PSO-LM-RBF神经网络模型可以更好的预测数据变化过程,改善了RBF神经网络的预测能力。
3 结 论
针对办公建筑的节能问题,提出了基于PSO-LM-RBF神经网络算法的建筑能效预测模型,并采用建筑实际能耗数据验证了模型的有效性。研究结果表明,PSO-LM-RBF神经网络模型的收敛速度(26个周期)显著高于改进之前(352个周期),收敛速度显著高于改进之前。改进后模型的预测结果更接近实际的输出负荷值,RBF神经网络的预测误差较大,PSO-LM-RBF神经网络模型预测精度更高,更接近实际负荷输出。改进后的算法的相对误差低于2.3%,平均、最大相对误差均显著低于改进前,说明PSO-LM-RBF神经网络模型可以更好的预测数据变化过程,改善了RBF神经网络的预测能力。由于时间和能力的不足,只是对办公建筑的总能耗进行了预测,并未涉及各分项系统的耗能情况,在今后的研究中,将更加注重建筑分项能耗的预测。

