Intelligent Dynamic Inversion Controller Design for Ball and Beam System

Ibrahim M.Mehedi,Abdulah Jeza Aljohani,Md Mottahir Alam,Mohamed Mahmoud,Mohammed J.Abdulaal,Muhammad Bilal and Waleed Alasmary

1Department of Electrical and Computer Engineering(ECE),King Abdulaziz University,Jeddah,21589,Saudi Arabia

2Center of Excellence in Intelligent Engineering Systems(CEIES),King Abdulaziz University,Jeddah,21589,Saudi Arabia

3Electrical and Computer Engineering,Electrical and Computer Engineering,TN,38505,United States

4Computer and Information Systems,Umm Al-Qura University,Makkah,Saudi Arabia

Abstract: The Ball and beam system(BBS)is an attractive laboratory experimental tool because of its inherent nonlinear and open-loop unstable properties.Designing an effective ball and beam system controller is a real challenge for researchers and engineers.In this paper,the control design technique is investigated by using Intelligent Dynamic Inversion (IDI) method for this nonlinear and unstable system.The proposed control law is an enhanced version of conventional Dynamic Inversion control incorporating an intelligent control element in it.The Moore-Penrose Generalized Inverse(MPGI)is used to invert the prescribed constraint dynamics to realize the baseline control law.A sliding mode-based intelligent control element is further augmented with the baseline control to enhance the robustness against uncertainties,nonlinearities,and external disturbances.The semi-global asymptotic stability of IDI control is guaranteed in the sense of Lyapunov.Numerical simulations and laboratory experiments are carried out on this ball and beam physical system to analyze the effectiveness of the controller.In addition to that,comparative analysis of RGDI control with classical Linear Quadratic Regulator and Fractional Order Controller are also presented on the experimental test bench.

Keywords: Ball and beam system(BBS);unstable system;internal model;PD controllers;IDI control;robust control

1 Introduction

The ball and beam system (BBS) is a standard laboratory experimental setup and serves as an essential benchmark to investigate and validate the performance of various control strategies[1].The tilt angle of the beam is the most significant action through which the ball position is controlled systematically by varying the tilt angle.It is an under-actuated open-loop unstable system having two degrees of freedom.The fundamental idea of BBS can be applied to a wide range of applications such as stabilizing the aircraft in its horizontal position while landing,tanker on-road carrying liquid,aircraft yaw roll control,goods handling problem by industrial robots,etc.

The control of an under-actuated system is an active research field having fewer control inputs than the state variables that need to be controlled.The experimental setup of BBS deals with the two loops control strategy.The outer loop is responsible for ball position control,whereas the inner loop is engaged for servo angle control.Due to its double loop control strategies,it is not easy to control this system using linear controllers[2].Therefore,several control techniques are proposed in the literature to investigate the tracking and stabilization problem of BBS[3-5].

A feedback linearization method is applied for BBS,which produces singularity and does not produce good results[3].A Fuzzy-based controller is investigated in[6],showing the tracking performance numerically without implementing it on a practical testbed.The Fuzzy and Neural Networks based algorithms are presented in[7,8].The robust control technique based on the sliding mode approach is also investigated for the ball balancing problem,see[9,10].A Backstepping controller is designed in[11]to simulate the tracking problem of BBS.An anti-windup compensator(AWC)control scheme is also demonstrated in[12].Similarly,the optimal performance of Model Predictive Control(MPC)is investigated to evaluate the tracking characteristics for ball and beam equipment[5].

Recent work was proposed designing a controller comprising two embedded loops based on linear fractional-order calculus [2].The outer-loop and inner-loop control the ball’s location on the beam and angle of servo gear,respectively.The prime focus of this method of control is to demonstrate a fractional-order control scheme to enhance efficiency,which is reported in several journals [13-17].However,the performance is unsatisfactory because an integer order traditional controller is related to the non-integer order integrator,which is used in the outer loop.

In addition to that,Nonlinear Dynamic Inversion(NDI)was also implemented for this ball and beam underactuated system,see [18].However,this control method requires the exact model of the plant dynamics.

Therefore,NDI control may possess certain shortcomings and limitations while developing the algorithms.This includes the simplified approximations to introduce the inverse model of plant dynamics,square dimensionality condition,useful nonlinearity cancellations,etc.

Recently a control law focused on the inversion principle is proposed known as Generalized Dynamic Inversion (GDI),which addresses the limitations of the classical NDI approach [19].The control objectives of GDI are defined in the form of differential state constraints which are calculated along the solution paths of the system dynamics.The control law is obtained by inverting the suggested constraints using Moore-Penrose Generalized Inverse (MPGI) [20].Further,the GDI algorithm is made intelligent by augmenting the switching term based on the concept of classical SMC principle to ensure robustness against parametric uncertainties and un-modeled dynamics while guaranteeing semi-global asymptotic stability conditions[21-25].

A two-loop control architecture is employed in this paper to solve the tracking and stabilization problem for two degrees of freedom under actuated BBS.A proportional derivative (PD) control is implemented in the outer loop to generate rotary servo angle commands based on the ball position on the beam.An intelligent version of GDI,Intelligent Dynamic Inversion(IDI),is used to process the inner loop’s angular command.Identical (baseline) control and switching (continuous) control elements make up this IDI control system.The baseline control enforces the constraint dynamics based on the deviation function of the rotary servo angle for stable attitude tracking,while the switching control ensures robustness against nonlinearities and external perturbations.As a result,the proposed control guaranteed a semi-global attitude tracking system and bounded tracking errors.Quanser’s BBS is used to simulate and perform laboratory experiments on the controller performance and compare the controller performance to existing control strategies.

The remaining sections of the paper are described as follows.The modeling of BBS is presented in Section 2.The two-loop control structure is discussed in Section 3.The classical PD control design for the outer position loop is presented in Section 4.The design implementation of IDI control for tracking the servo angle command is given in Section 5.The detailed stability analysis that will guarantee semi-global asymptotic stability was illustrated in Section 6.Controller validation through computer simulations and experimental findings are reported in Sections 7 and 8.Finally,the concluding remarks are given in Section 9.

2 Description of BBS

Quanser developed BBS,a benchmark laboratory test bench [1],to validate control algorithms that are defined relative degrees with nonlinear attributes.The two significant ball and beam setup components are the ball and beam unit and rotary servo unit.One end of the finite length beam is fixed by a shaft,whereas the other end is connected to the rotary servo unit,as shown in the schematic diagram in Fig.1.Therefore,this unstable architecture is well known as an open-loop system in control technology.The core objective is to orient and stabilize the ball placed on the beam according to the commanded reference input profile.In Fig.1,xis the linear displacement ball,mbis the mass,rbis the beam’s radius,andJbis the ball’s momentum,respectively.The relative angle of the beam concerning the horizontal plane is denoted byα,whereas the gravitational acceleration is mentioned byg.The expression of the linear acceleration of the ball is given as Eq.(1).

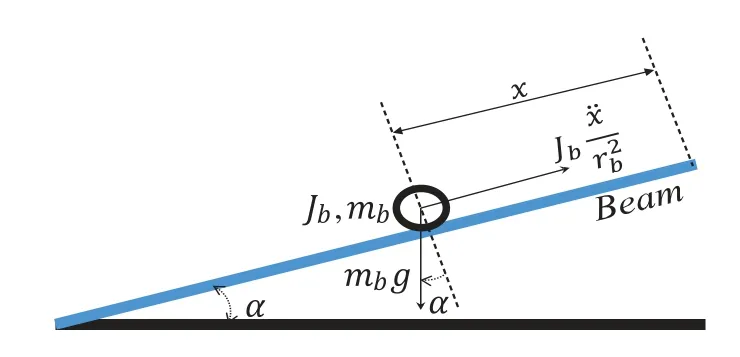
Figure 1:Ball and beam system

Similarly,the relation between the beam angleαand servo angleθl(t)is expressed as

whereLbeamis the length of the beam andrarmis the gap between the rotary servo output gear and the coupled joint.To relate the linear displacementxwith the rotary servo angleθ,place the expression ofsinα(t)in the linear acceleration equation given by Eq.(2),it implies

The second major component of the ball and beam setup is the rotary servo base unit which comprises a DC motor with a gearbox,as shown in Fig.2.The subscriptmrepresents the motor attributes in the given schematic,whereaslcharacterizes the load shaft variables.In the rotary servo unit,the resistance is denoted byR,Lis the inductance,ωis the angular speed,τis the applied torque,Jis the moment of inertia,andBstands for the viscous friction.The variableebrepresents the backelectromotive voltage,wherekmis the back-emf constant.To realize the dynamical model of the rotary servo unit,the mechanical and electrical systems are combined to form the relationship between the angular speed of the motor load shaftωland the applied controlled voltageVm.The dynamical system is represented by the following equations

where the equivalent moment of inertiaJeqis expressed as

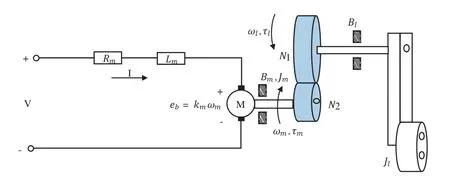
Figure 2:Rotary servo unit

and the equivalent damping termBeqvis given by

In the expressions of the equivalent moment of inertia and damping,ηgandηmrepresent the efficiency of the gearbox and motor,respectively.The motor torque constant is denoted bykt,andkgis the gear ratio.The actuator gainAmis computed as

The numerical value of the BBS parameters is listed in Tab.1,see[1,26].

3 Cascade Control Architecture

A cascade control architecture based on the time separation principle is proposed to control the ball’s position on the beam,as shown in Fig.3.Based on the measured ball positionx,the outer positional loop computes the desired angleθldof the servo load shaft by engaging the classical PD control.The inner fast attitude loop incorporates IDI control to track the desired angleθldby generating the corresponding motor controlled voltageVsuch that the desired ball position on the beam is achieved in minimal time.

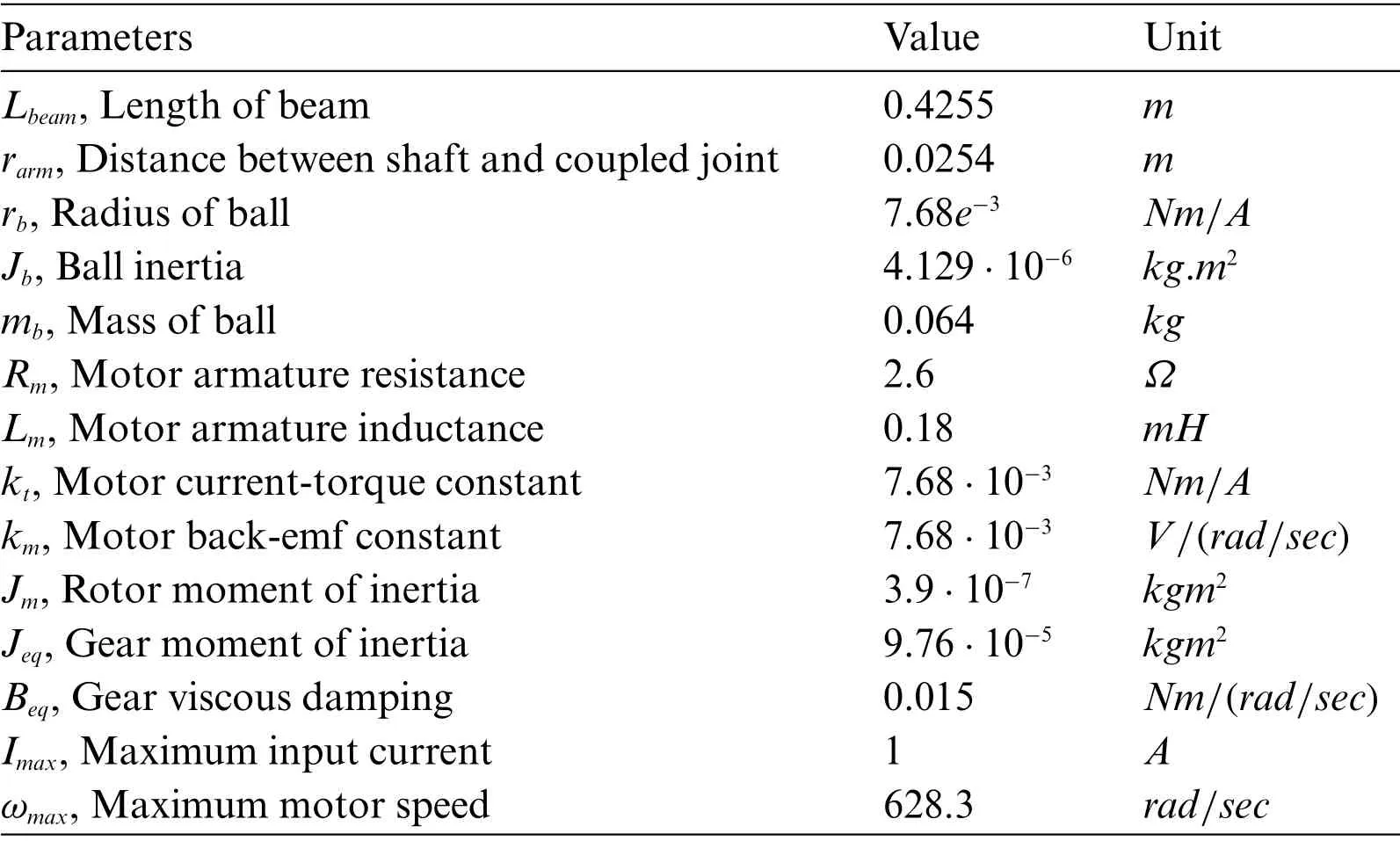
Table 1:BBS specifications

Figure 3:Cascade control architecture

4 Outer Loop PD Control Design

Given the desired and actual ball’s position,i.e.,xdandx,the classical PD controller is engaged in the outer loop to generate the desired servo angle commandθldfor the inner loop to minimize the positional error of the ball placed on the beam.The asymptotically stable virtual(desired)dynamics to computeθldbased on the positional error of the ball in the horizontal plane is expressed as

wherekpandkdare controller gains chosen to calculate the suitable value ofθldsuch thatxapproachedxdin minimum time.It is noteworthy to mention here that the position feedback of the ball is acquired from an analog sensor with its inherent noise.By taking its derivative,it will generate an amplified high-frequency signal transmitted to the inner loop via feedback which causes the grinding noise in the motor.The derivative is replaced by a first-order filter governed following dynamics to compensate for this effect.

whereωfrepresents the cutoff frequency,whose value is set to be 6.28 rad/s.

5 Attitude Control Using IDI

This section discussed the design and implementation of IDI control for attitude control of the rotary servo unit of BBS.The proposed non-square inversion-based intelligent controller proves to be an efficient and effective control strategy to deal with complex nonlinear systems.The control law comprises two major components,i.e.,an equivalent or baseline control and a switching control component.The general form of IDI control law is expressed as follows

The first componentueqrepresents the baseline controller,which enforces the prescribed constraint dynamics based on the attitude deviation function for stable attitude tracking.On the other hand,urbtrepresents the discontinuous control element whose design principle is based on the classical SMC approach to address robustness against uncertain dynamics,parametric variations,and external disturbances.

5.1 Baseline Control Design

The equations of motion of rotary servo unit angular rate dynamics given by Eq.(5)is expressed as

whereζθl=x1e2θl=x1(θl-θld)2andζωl==x2(ωl-ωld)2are the deviation functions andωlis the angular speed.The order of the constraint equation is equal to the relative degree of the respective controlled variable.The coefficientsc1,c2,andc3are selected such that the characteristic polynomials are given by Eqs.(13),and(14)is Hurwitz,such thatζθl→0 andζωl→0 ast→∞[19].Computing and substituting the time derivatives in the constraint dynamics given by Eqs.(13)and(14)yields the following under-determined equivalent algebraic system.

where the elements of the controls coefficient column vector function A:Rn×[t0,∞)→R2×1is given by

A1=2x1eθlG

A2=2x2eωlG

and the elements of the controls load vector function B:Rn×[t0,∞)→R2×1are given as

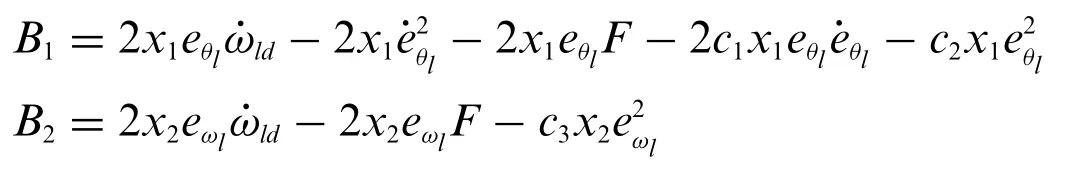
The baseline or equivalent controlled voltageVmeqis computed by inverting the algebraic system given by Eq.(15)using MPGI yields the following expression

where A+represents the MPGI of A defined as

Remark 1:The matrix A2×1appeared to be a tall matrix,which causes the value ofPto become zero by using the property of pseudo-inverse A+A=1.Hence the under-determined nature of constraint dynamics does not qualify with the benefit of the null control vector due to the ineffectiveness of the null projection matrix.Hence,the null control is supposed to be incompetent and not considered in the present control design methodology.

5.2 Switching Control Design

A suitable discontinuous control element is determined to solve the reachability problem,which ensures robustness against parametric uncertainties,system nonlinearities,and external disturbances.The resultant GDI-SMC or IDI control law is constructed to be of the following form

where s=[sθl sωl]Tis an appropriate switching surface vector,whose vector elements are defined as

Moreover,K is 2 × 2 diagonal gain matrix with positive valued diagonal elementsk1andk2,ensuring that the sliding mode dynamics are maintained and attained.Therefore,the controlled voltageVmgiven by the Eq.(18)is reasonably competent to attract the sliding surfaces given by Eqs.(19)and(20)and enforce the system trajectories to slide along the sliding surfaces.

6 Stability Analysis

The time derivatives of the sliding surfaces are evaluated as

It has been observed that the asymptotic convergence of the sliding surfacessθlandsωlto zero implies the asymptotic realization of the constraint dynamics given by the Eqs.(13)and(14),and its equivalent algebraic form given by Eq.(15).Hence,the sliding vector s is defined as

To prove the asymptotic convergence of the error dynamics,place the control lawVmgiven by Eq.(18)in sliding mode dynamics given by Eq.(23),resulting in

Consider the following positive definite Lyapunov candidate function

The time derivative ofVis computed as

The 2-(induced) norms of AA+and AA+-I2×2are unity.It follows that≤0 is guaranteed ifσmin(K)＞‖ B(x(0),0)‖,whereσminis the minimum singular value function.Moreover,because=0 occurs only at s=02,it follows Lassale’s principle [27]that s=02is attractive.Moreover,the discontinuous term in the right-hand side of Eq.(26)implies that this condition on K guarantees finite-time convergence of s and ˙sto the zero vectors,which implies asymptotic convergence ofeθlandeωlto zero.Finally,because it is assumed that the matrix gain K can be increased arbitrarily such that the stability condition is satisfied for any initial state condition,it follows that the design guarantees semi-global asymptotic stability of

7 Numerical Simulation

This section investigates the performance of IDI control law through computer simulations on the dynamical simulator of BBS developed by considering the model of ball and beam unit given by Eq.(3)and the model of rotary servo unit given by Eqs.(4)and(5).The simulation environment is created in Simulink/Matlab,in which the closed-loop performance is evaluated by commanding the square wave profile having an amplitude of ±20mwith 0.05Hzfrequency,assuming nominal system parameters.The initial condition of the system state vector is set as[0 0 0 0 0 0]The time histories of the position tracking curve of the ball is shown in Fig.4,which is quite appealing.The inner loop rotary servo angle tracking performance using IDI control is depicted in Fig.5,which demonstrates faster convergence towards the angular reference command.Finally,the servo motor controlled voltage well within the saturation limit is displayed in Fig.6.

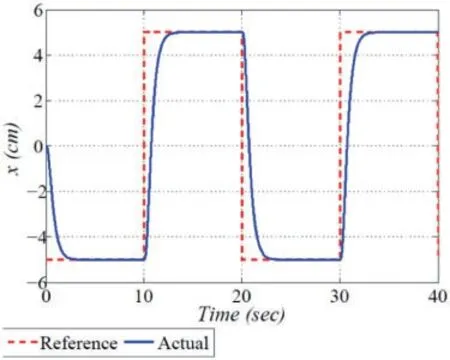
Figure 4:Simulations:ball position

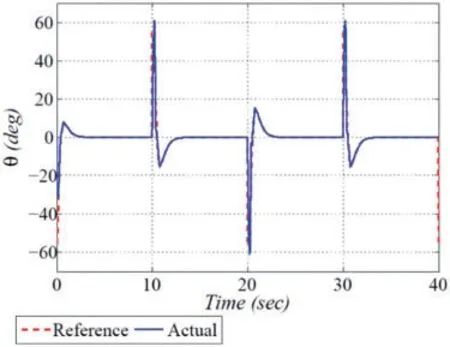
Figure 5:Simulations:beam angle

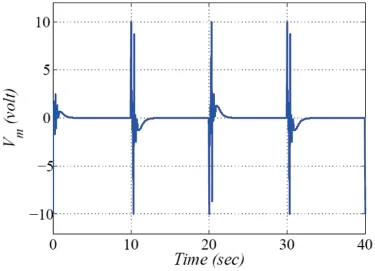
Figure 6:Simulations:controlled voltage

8 Experimental Results

To investigate the real-time performance of balancing the ball on a beam,the IDI control law developed in Section 5 is implemented on Quanser’s ball and beam real hardware,as shown in Fig.7,which proves to be a benchmark testbed for testing and validating control techniques.

Figure 7:Experimental setup

The experimental setup comprised the power module VoltPAQ-X1 for supplying voltage to the rotary servo motor module.The servo motor is placed at the right corner of the beam to move the beam in an upward and downward direction.The ball placed on the beam rolls on the track accordingly by changing the slope of the beam.The ball position and the angular position feedback commands are sent to the computer through Quanser’s Q8-USB data acquisition card.The communication between Simulink/MATLAB and the experimental hardware is accomplished through the QUARC software.The sampling time is chosen to be 2msfor all the experiments.

8.1 Step Response Analysis

In this analysis,the core objective is to present the comparative analysis of IDI control with classical Linear Quadratic Regulator(LQR)and Fractional Order Control(FOC)strategies.The ball is commanded to follow the step input profile in this setup.The initial position of system states arex=-18cm,=0cm,θl=0deg,and=0deg,whereas the desired step command is set to bexd=10cm.The three control methodologies were implemented on a practical BBS test bench,and the tracking curves of ball position,beam angle,and the controlled voltages are shown in Figs.8-10.It is evident from Fig.8 that the response curves of positional tracking with IDI control are faster in terms of rising time and settling time.

Figure 8:Experimental results:ball position

Figure 9:Experimental results:attitude tracking

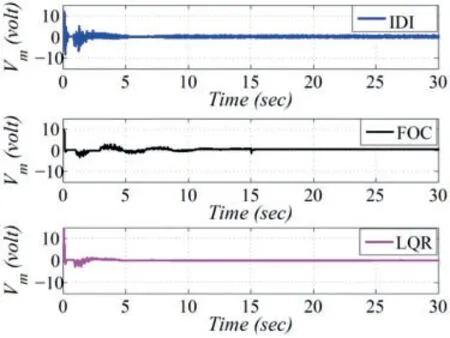
Figure 10:Experimental results:controlled voltage

Furthermore,the FOC suffers from high overshoot,whereas many steady-state errors were observed in the LQR response.On the other hand,the IDI controller demonstrates very stable time-domain performance near reference input with less overshoot and steady-state error.The time evolution of desired and actual angular profiles and the time histories of the controlled voltages generated in response to the step input command are shown in Figs.9 and 10,respectively.

8.2 Disturbance Rejection Capability

This section highlighted the disturbance rejection capability of the IDI controller when the ball is subjected to some manual disturbances.The ball position on the beam in a steady state is stimulated by tapping the ball at different time instants.The ball position plot under the effect of disturbances is shown in Fig.11.It is evident that when disturbances are applied,the ball position is perturbed but immediately returns to its stable position by control reaction and re-stabilized.The jerks appeared in the angular profile due to manual perturbations,which are depicted in Fig.12.The controlled voltage under the supplied capacity is displayed in Fig.13,whose magnitude fluctuates in response to the applied disturbances.The experimental results demonstrate better disturbance rejection capability and intelligent attributes of IDI control.

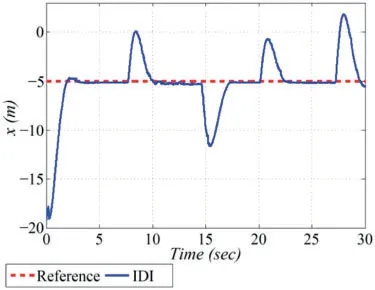
Figure 11:Experimental results:ball position

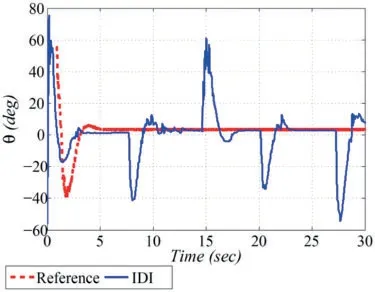
Figure 12:Experimental results:attitude tracking

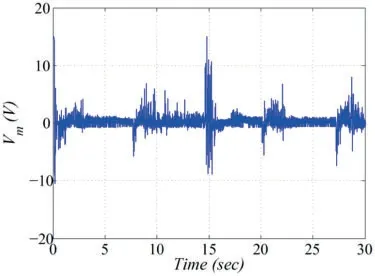
Figure 13:Experimental results:controlled voltage

8.3 Square-wave Tracking

In this plot,the controllers’capability is further analyzed by commanding a reference square wave profile with an amplitude of ±20mwith 0.05Hzfrequency and the variation of 20% in the system dynamical parameters.The time evolution of the critical performance indices is illustrated in Figs.14-16.The smooth tracking response of the ball’s position placed on the beam in response to the square wave input command is shown in Fig.14.The rotary servo angular position tracking curve required to steer the ball to follow the square waveform command and the control effort in the form of generated controlled voltage are shown in Figs.15 and 16,respectively.

Figure 14:Experimental results:ball position

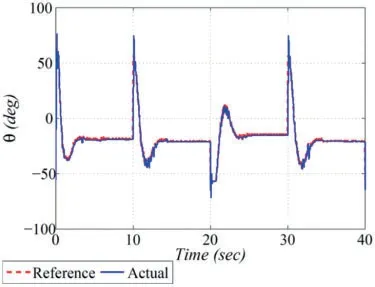
Figure 15:Experimental results:attitude tracking

Figure 16:Experimental results:controlled voltage

While examining the different behaviors of the controller response in the simulation and experimental results,it is claimed that the proposed controller proves itself a reasonable control approach for stabilizing the under-actuated electro-mechanical systems.

9 Conclusion

This paper investigates the performance of IDI control for a standard nonlinear ball and beam unstable system.A two-loops structured control is implemented in which PD control is responsible for generating the desired servo angle command based on the positional error of the ball placed on the beam.Furthermore,IDI control is engaged in the inner loop for precise attitude tracking.The results are verified through computer simulations and experimental studies in a MATLAB environment.Furthermore,a comparative analysis is presented,which exhibits the superior performance of IDI control over LQR and FOC in terms of faster error convergence with lesser steady-state error.Hence the proposed methodology is quite appealing and feasible for practical electro-mechanical systems.

Acknowledgement:The authors extend their appreciation to the Deputyship for Research &Innovation,Ministry of Education in Saudi Arabia for funding this research work through the Project Number(IFPRC-023-135-2020)and King Abdulaziz University,DSR,Jeddah,Saudi Arabia.

Funding Statement:This research work was funded by Deputyship for Research &Innovation,Ministry of Education in Saudi Arabia under Grant No.(IFPRC-023-135-2020).

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.