一种流形正则化非负矩阵分解的lncRNA-疾病关系预测方法

董文文,林志毅

(广东工业大学 计算机学院,广州 510006)

E-mail:lzy291@gdut.edu.cn

1 引 言

近年来研究表明,非编码RNA(ncRNA)与蛋白质的相互作用对生物过程如蛋白质合成,基因表达,RNA加工和发育调控等具有积极影响[1].随着生物技术的不断发展,ncRNA尤其是长非编码RNA(lncRNA)已在各种生物学过程中发挥了重要作用[2].研究表明某些lncRNA的失调和突变与人类疾病[3]有关,例如肺癌[4]、宫颈癌[5]、骨肉瘤[6]、颅内动脉瘤[7]等.因此,一些学者希望通过了解lncRNA的机制来探索使用lncRNA作为辅助治疗工具的可能性[8,9].目前已经建立的数据库如LncRNADisease[10]、NRED[11]、Lnc2Cancer v2.0[12]、MNDR V2.0[13]和NONCODE[14]等有助于lncRNA与疾病关系的研究.但是,由于进行生物学实验或临床研究需要大量成本和时间,而且这些数据库中包含的lncRNA-疾病的关系很少,这对研究人员是一个限制.

因此,近年来研究人员在生物信息学领域开发了许多计算方法来计算潜在的lncRNA-疾病关系[15].目前的lncRNA与疾病关系预测方法可大致分为两类.一类是基于构造的生物网络来预测lncRNA与疾病间的关系[16,17].例如,Yu等人[18]提出双随机游走(BRWLDA)方法考虑了lncRNA相似性和疾病相似性之间的结构差异,使用lncRNA功能相似性和疾病语义相似性构建了两个网络,在这两个网络上使用多个随机游动来预测潜在的lncRNA-疾病关系.但是,BRWLDA仍然具有随机游走方法的缺点.Xie等人[19]提出基于不平衡随机游走(LDA-LNSUBRW)的计算方法,但该方法仅考虑单一相似性,仍然存在数据稀疏性等问题.另一类方法是基于机器学习算法预测lncRNA-疾病的关系[20].近年来,基于矩阵分解的机器学习算法广泛应用于异构数据的融合[21,22].例如,Fu等人[23]开发的基于矩阵分解的数据融合方法(MFLDA),该方法可以很好地利用异构数据源并应用于各种类型实体之间的相关性预测.但是该方法的性能取决于最佳参数的选择,目前尚无法有效的解决最佳参数的选择问题.Gao等人[24]提出基于高斯核函数的双重稀疏协同矩阵分解方法(DSCMF)来推断潜在的lncRNA与疾病关系.DSCMF结合了矩阵分解和协同过滤,但是,如何更好地选择整合相似性的方法来改善预测结果是一个需要解决的问题.Xuan等人[25]提出PMFILDA 方法,该方法在矩阵分解基础上增加了概率计算.但是,其结果在很大程度上受miRNA-疾病关系网络的影响,预测精度仍有进一步提升的空间.

针对以上方法仍然存在的数据源来源单一、数据稀疏、预测精度低等问题,本文提出一种新的流形正则化的非负矩阵分解计算方法(MRNMFLDA)来预测lncRNA与疾病的关系.首先,MRNMFLDA使用相似性网络融合方法来分别整合lncRNA的两种相似性与疾病的两种相似性,实现了两种数据源的有效融合,解决了单一相似性矩阵的数据稀疏性问题.然后,本方法通过构建标签加权矩阵、引入流形正则化约束的非负矩阵分解算法来预测lncRNA与疾病潜在的关系,充分考虑了数据内部的几何结构的联系,既有效防止过拟合问题并显着提高了预测性能.实验结果表明:MRNMFLDA方法在留一交叉验证和5折交叉验证的方案中AUC值分别达到0.8927和0.8635±0.0054与其他方法(PMFILDA,LDA-LNSUBRW ,DSCMF,BRWLDA )相比具有优越的性能.

2 数据准备

2.1 人类lncRNA-疾病关系数据

本文从LncRNADisease数据库[10]中下载最新的lncRNA-疾病关系数据,该数据集包含115种lncRNA和178种疾病,以及540种经过实验验证的关系.该数据集将用作lncRNA与疾病关系预测的训练数据集,并用作交叉验证实验的标准.从上述已知关系中,我们可以得到lncRNA-疾病邻接矩阵A∈Rm×n,其中m和n分别是lncRNA和疾病的数目,如果lncRNAi与疾病j相关,则A(i,j)为1.否则为0.

2.2 疾病语义相似性

本文采用有向无环图(DAG)用来描述疾病的语义相似性[26].对于疾病C,DAG(C)=(D(C),E(C)),其中D(C)表示自身及其祖先节点的集合,E(C) 表示D(C)中连接各个节点边的集合.假设疾病t属于D(C),则疾病t对C的语义贡献定义如下:

DC(t)=1,t=C
max0.5*DC(t′)|t′∈t的孩子,t≠C

(1)

疾病C的语义值定义如下:

D(C)=∑t∈DAG(C)DC(t)

(2)

A和B两种不同疾病间的语义相似性DSS计算为如下:

DSS(A,B)=∑t∈DAG(A)∩DAG(B)(DA(t)+DB(t))D(A)+D(B)

(3)

其中t是D(A)和D(B)中的常见疾病DA(t)和DB(t)分别表示疾病t对疾病A和B的贡献.

2.3 lncRNA功能相似性

本文采用Chen等人[27]的计算lncRNA功能相似性的方法,用d表示疾病,疾病的集合设为D={d1,d2,…,dk},则两种不同lncRNA的功能相似性计算如下:

SIM(d,D)=max1≤i≤kDSS(d,di)

(4)

其中DSS(d,di)代表d和di之间疾病的语义相似性值.LncRNAli和lj之间的功能相似性由LFS(li,lj)表示如下：

LFS(li,lj)=∑d∈DiSIM(d,DJ)+∑d∈DjSIM(d,Di)|Di|+|Dj|

(5)

2.4 LncRNA / disease高斯核相似性

基于功能相似的lncRNA与疾病具有相似的相互作用模式的假设,利用已知的lncRNA与疾病的关联网络,计算它们之间的高斯距离[15,28].首先,我们将疾病d(i)的关联情况SS(d(i))表示在已知的lncRNA-疾病关系网络中的二进制向量编码,0代表不存在关联关系,1代表存在关联关系.然后,疾病d(i)与疾病d(j)之间的高斯核相似性GD的计算公式如下:

GDd(i),d(j)=

exp-γ′dSSd(i)-SSd(j)2

(6)

在先前研究的基础上,本文最终确定了γ′d= 1[29]的参数.γd是用于控制高斯核频宽的参数,可以改善模型的性能.调整此参数可以使疾病之间的相似性更加标准化.γd的计算公式如下:

γd=γ′d1nd∑ndi=1SSd(i)2

(7)

LncRNA高斯核相似性GL计算方法同上.

3 流形正则化非负矩阵分解的lncRNA-疾病关系预测方法(MRNMFLDA)

为防止过度拟合并显著提高学习性能,本文提出一种新的流形正则化非负矩阵分解方法(MRNMFLDA)来预测lncRNA与疾病的关系.MRNMFLDA采取3个步骤来预测lncRNA与疾病的关系.首先,MRNMFLDA使用相似性网络融合方法来整合lncRNA功能相似性与lncRNA高斯核相似性,得到lncRNA网络融合相似性.同样的,MRNMFLDA使用相似性网络融合方法来整合疾病的语义相似性和疾病高斯核相似性得到疾病网络融合相似性.然后,MRNMFLDA对lncRNA网络融合相似性矩阵和疾病网络融合相似性矩阵进行了正则化,将两个正则化项以及构建的标签加权矩阵合并到非负矩阵分解目标函数中,并引入了迭代算法来优化目标函数.最后, lncRNA-疾病潜在的关系是通过构建的流形正则化约束的非负矩阵分解算法来预测的.MRNMFLDA方法的伪代码如表1所示.MRNMFLDA方法的流程图如图1所示.

3.1 相似性网络融合

使用上述相似性计算方法,得到4个相似性矩阵,lncRNA功能相似性矩阵LFS,lncRNA高斯核性矩阵GL,疾病语义相似性DSS,疾病高斯核相似性矩阵GD.然而,仅使用单一的相似性矩阵无法提供多方面的生物学信息,存在数据稀疏性问题.因此,如何使用合理有效的方法融合lncRNA和疾病的两个相似性矩阵,解决单一相似性矩阵的数据稀疏性问题,是本文需要解决的第1个关键问题.此外,如何能够有效利用数据间几何结构之间的关联从而提高方法的预测性能是本文着重解决的第2个关键问题.

表1 MRNMFLDA方法的伪代码Table 1 Pseudocode of MRNMFLDA method

图1 MRNMFLDA方法的流程图Fig.1 Flowchart of MRNMFLDA method

针对第1个关键问题,本文提出了一种非线性的相似性网络融合方法来整合lncRNA和疾病的相似性.相似性网络融合(简称SNF)是一种多组学融合的方法,多应用于癌症数据分析[30],miRNA-EF相互作用数据分析[31]和lncRNA-miRNA相互作用分析[32].它能够捕获不同数据的全局和局部特征.对于lncRNA的相似性,SNF定义如下:

Gfl(i,j)=LFS(i,j)2∑a≠iLFS(i,a),i≠j12,i=j

(8)

Lfl(i,j)=LFS(i,j)∑a∈NiLFS(i,a),j∈Ni0,otherwise

(9)

Ggl(i,j)=GL(i,j)2∑a≠iGL(i,a),i≠j12,i=j

(10)

Lgl(i,j)=GL(i,j)∑a∈NiGL(i,a),j∈Ni0,otherwise

(11)

Ffl(b+1)=Lfl×Ggl(b)×LflT

(12)

Fgl(b+1)=Lgl×Gfl(b)×LglT

(13)

Fl=Ffl+Fgl2

(14)

其中Gfl,Lfl,Ggl和Lgl分别表示lncRNA功能相似性的全局矩阵,lncRNA功能相似性的局部矩阵,lncRNA高斯核相似性全局矩阵,lncRNA高斯核相似性局部矩阵.Ni代表lncRNA i 的K近邻.a是最近邻居的数量.对于不在最近邻居中的邻居,该值转换为0.公式(8)-公式(11)的计算过程可增强网络中的强链接,消除网络中的弱链接,从而大大降低了数据噪声干扰.Ffl和Fgl分别表示lncRNA功能相似性的融合矩阵和lncRNA高斯核相似性的融合矩阵.公式(12)和公式(13)经过b次非线性的迭代过程,每次迭代交换不同原始网络的信息,得到网络融合矩阵,使得融合效果最佳.Fl表示lncRNA网络融合相似性矩阵.疾病网络融合相似性矩阵Fd可以用相似的方式获得.

3.2 引入标签加权矩阵和流形正则化的非负矩阵分解算法

3.2.1 标准的非负矩阵分解算法

非负矩阵分解(NMF)是一种有效的数据处理技术,其目的是找到两个低秩非负矩阵,两者的乘积是原始矩阵的最佳近似表示.NMF可以将lncRNA-疾病矩阵A∈Rm×n分解为两个低秩的矩阵,即U∈Rm×K和V∈Rn×k(k≤min(m,n) ),且A≈UVT.在这里,我们用数学公式将与疾病相关的lncRNA预测问题表达为以下目标函数:

minU,V‖A-UVT‖2Fs.tU≥0,V≥0

(15)

其中‖·‖F代表Frobenius范数.Lee等人[33]提出的迭代更新算法可以使上述目标函数最小化.

3.2.2 构建标签加权矩阵

lncRNA-疾病邻接矩阵A的元素由已知的lncRNA与疾病关系标签信息和未知的lncRNA与疾病关系信息标签信息组成.与单一相似性矩阵类似,A也是一个稀疏矩阵,其中大多数值为零,并且这些零值可能具有未知的关系,即存在lncRNA-疾病邻接矩阵的稀疏性问题.这种情况可能会导致在预测未发现的lncRNA-疾病关联中表现不理想.Peng等人[34]提出构建标签加权矩阵的方法来解决基因与蛋白质原始关系矩阵的稀疏性问题.鉴于此,本文通过构建新的标签加权矩阵的方法解决lncRNA-疾病邻接矩阵的稀疏性问题,并将构建的标签加权矩阵引入到本文的改进NMF中.本文的目标是使用已知的标签信息来预测未知的lncRNA和疾病的关系.因此,我们设Y为m×n的标签加权矩阵.如果已知lncRNAi和疾病j的相应关系,则将Y的元素设为非零值,否则将Y的元素设为0.考虑到某些lncRNA和疾病暂时没有已经验证的联系,我们为Y设置了不同的权值.Y(i,j)的权重设置如下:

Y(i,j)=1,ifA(i,j)isknownandA(i,j)=1
0.5,ifA(i,j)isknownandA(i,j)=0
0,ifA(i,j)isunknown

(16)

3.2.3 MRNMFLDA目标函数

原始数据矩阵的维度较高,含有许多冗余数据.标准NMF能够将高维数据以低维数据形式近似表示,适合lncRNA或疾病关系数据的处理.但是,标准NMF只是在欧式空间中对数据进行降维,不能有效利用lncRNA或疾病关系数据内部空间的几何结构,而关系数据的几何结构往往表达了数据的真实表示形式.

因此,为了解决第二关键问题,且提高标准NMF的预测能力,本文在标准NMF基础上,基于流形学习的思想提出了改进的NMF.

流形学习思想基于局部不变的假设,认为如果两个数据点在原始几何结构中接近,则两个数据点的新表示形式也接近[35].为了保留固有的几何结构,假设两种lncRNA在lncRNA网络中连接,则lncRNA低秩矩阵中两种lncRNA的表示形式应接近.同样,具有关系的疾病在疾病低秩矩阵中应显示相似的表示形式.目前,Yan等人[36]已将流形学习的思想引入到标准NMF中,并成功地应用于药物-靶蛋白关系预测.

基于流形学习的思想,本文提出的改进NMF是将两个相似性矩阵(疾病网络融合相似性矩阵,lncRNA网络融合相似性矩阵)正则化项以及构建的标签加权矩阵分解项合并到NMF目标函数中,来发掘数据内部的几何结构,进而提高lncRNA-疾病关系预测的精度.其中,新的NMF目标函数如下:

minOBJ(U,V)=Y⊙(A-UV)2F+λltrUTLlU+
λdtrVLdVT+αU2F+βV2F

(17)

上式中⊙代表哈达玛积,tr(UTLlU)代表lncRNA网络融合相似性矩阵Fl的流形正则化项,Ll∈Rm×m是Fl的一个拉普拉斯矩阵.Dl∈Rm×m是对角矩阵,其对角线元素对应值是矩阵Fl的行总和(或列总和),Ll=Dl-Fl.类似地,tr(VLdVT)是疾病网络融合相似性矩阵Fd的流形正则化项.为了避免过拟合问题, 采用‖U‖2F和‖V‖2F来惩罚U和V的幅度.λl和λd是控制Fl正则项和Fd正则项的正则化参数,α和β是平滑参数.

3.2.4 迭代更新U和V,得到预测评分矩阵

为了获得U和V的解,首先对U和V中的值进行随机初始化,然后使用公式(18)和公式(19)中的更新规则对其进行迭代更新,重复该过程,直到根据准则(等式(20))判断算法收敛为止.U和V的具体求解过程如下:

Ui,k←Y⊙AVT+λlFlUY⊙(UV)VT+λlDlU+αUUi,k

(18)

Vk,j←UT(Y⊙A)+λdVFdUT(Y⊙(UV))+λdVDd+βVVk,j

(19)

OBJt-OBJt-1OBJt<ε

(20)

其中OBJt代表目标函数在迭代步骤t时的值.ε是一个小的正数,在此设置为10-6.再根据公式(18)和公式(19)的更新规则,更新U和V之后直到收敛,我们获得了最终的lncRNA预测评分矩阵为Score=U*VT.最后,基于预测评分矩阵,对与疾病相关的lncRNA进行了排名(如表2-表4所示).通常,预测得分最高的lncRNA与相应疾病相关的可能性更高.

表2 预测与肺癌相关的lncRNATable 2 Predicted lncRNAs associated with lung cancer

表3 预测与宫颈癌相关的lncRNATable 3 Predicted lncRNAs associated with cervical cancer

表4 预测与骨肉瘤相关的lncRNATable 4 Predicted lncRNAs associated with osteosarcoma

4 结果和讨论

在本文中,使用留一交叉验证(LOOCV)[37]和五折交叉验证(5-fold-CV)[38]两种方法来评估MRNMFLDA方法的预测准确性.LOOCV是使用540种lncRNA疾病关系中的一种作为测试样本,其余的作为训练集.在五折交叉验证中,将所有lncRNA-疾病关系矩阵随机分为5组,其中一组用作测试集,而其他4组用作训练集.预测分数由MRNMFLDA计算并排序,选择特殊排名位置作为阈值,并用(ROC)曲线下面区域面积(AUC值)作为性能指标来评估预测性能.ROC曲线可以绘制不同阈值下的真阳性率(TPR)和假阳性率(FPR)之间的关系.如果AUC接近1,则预测性能会更好.

4.1 参数讨论

参数的取值对算法的性能有很大的影响.在本文提出的预测方法中有6个参数:SNF中的邻居数a;迭代次数b;相似性正则化权重参数λl和λd;平滑参数α和β.本文讨论其中一个参数的影响时,预先给定其他5个参数,选出该参数的最优值后再进行逐个调整.本文在LOOCV中讨论参数对MRNMFLDA方法性能的影响.对于SNF中a和b,参数调整范围是{1,2,3,…,10},实验结果图2显示当a=2,b=2时, AUC值最高.对于非负矩阵分解部分λl和λd的参数调整范围是{10-4,10-3,10-2,10-1},实验结果图2显示,当λl=10-1和λd=10-1时,AUC值最高.平滑参数α和β的参数调整范围为{0.1,0.2,0.3,…,1},实验结果图2显示,AUC值随着参数增加呈递减趋势,所以当α=0.1和β=0.1时,此时AUC值最高.说明当a=2,b=2,λl=10-1,λd=10-1,α=0.1和β=0.1时,算法的预测性能最佳.

图2 参数a,b,λl,λd,α,β在LOOCV中对方法的影响Fig.2 Effect of parameters a,b,λl,λd,α and β on the method in LOOCV

4.2 评估预测性能

4.2.1 与单一相似性网络的比较

MRNMFLDA方法的性能评估分为两部分:网络融合相似性与单一相似性比较性能评估,MRNMFLDA方法与其他预测方法的性能评估.

网络融合相似性与单一相似性比较性能评估考虑以下情况:1)引入lncRNA网络融合相似性F^l和疾病网络融合相似性Fd的预测性能;2)仅考虑LncRNA高斯核相似性(GL)和疾病高斯核相似性(GD)的预测性能;3)仅考虑lncRNA功能相似性(LFS)和疾病语义相似性(DSS)的预测性能.

对比结果中图3显示本文采用的网络融合相似性网AUC值(0.8927)高于仅考虑GL、GD的AUC值(0.8230)和仅考虑LFS、DSS的AUC值(0.8073),表明本文提出的相似性网络融合方法SNF来整合lncRNA与疾病的相似性,能够显著提高预测性能.

4.2.2 与其他方法比较

为了更好地评估MRNMFLDA方法的预测性能,本文首先采用LOOCV将MRNMFLDA与其他预测方法(PMFILDA[25],LDA-LNSUBRW[19],DSCMF[24],BRWLDA[18])进行了比较.显然,如图4所示MRNMFLDA的AUC为0.8927,高于其他方法的AUC(PMFILDA 0.8744,LDA-LNSUBRW 0.8703,BRWLDA 0.7848,DSCMF 0.7917).为了进一步验证MRNMFLDA的预测性能,本文采用5-fold-CV进一步验证预测性能.如图5所示,MRNMFLDA的AUC值为0.8635±0.0055,高于其他方法的AUC(PMFILDA 0.8522±0.0075,LDA-LNSUBRW 0.8374±0.0047,DSCMF 0.7510±0.0081,BRWLDA 0.7469±0.0064).以上结果表明,本文提出的方法在这5种方法中预测性能最佳.

图3 基于网络融合相似性与单一相似性在LOOCV中的ROC曲线和AUC值Fig.3 ROC curve and AUC value of network fusion similarity based and single similarity based in LOOCV

图4 5种方法(MRNMFLDA,PMFILDA,DSCMF,BRWLDA,LDA-LNSUBRW)在LOOCV中的ROC曲线和AUC值Fig.4 ROC curve and AUC values of the five methods in the LOOCV (MRNMFLDA,PMFILDA,LDALNSUBRW,DSCMF,BRWLDA)

4.3 案例分析

为了进一步验证MRNMFLDA方法预测lncRNA与疾病潜在的关系的能力,本文选择了肺癌(lung cancer),宫颈癌(cervical cancer)和骨肉瘤(osteosarcoma)3种癌症疾病进行案例研究.首先根据MRNMFLDA方法预测得分结果筛选排名前10的lncRNA,再从Lnc2Cancer和MNDR数据库中查找这些lncRNA与对应疾病的确证关系.表2-表4结果显示预测得分中排名前10的lncRNA在数据库中得到验证的数量分别为10,9,8,说明了本预测方法结果的可靠性.

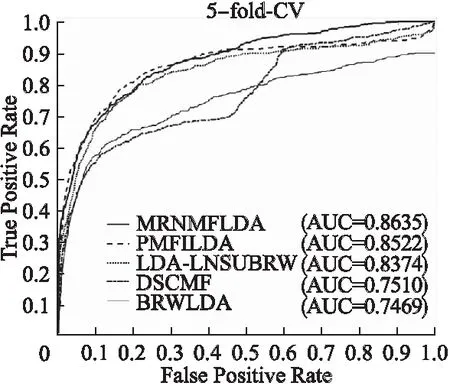
图5 5种方法(MRNMFLDA,PMFILDA,DSCMF,BRWLDA,LDALNSUBRW)在5-fold-CV中的的ROC曲线和AUC值Fig.5 ROC curve and AUC values of the five methods in the 5-fold-CV (MRNMFLDA,PMFILDA,LDALNSUBRW,DSCMF,BRWLDA)

以肺癌为例,lncRNA与肺癌的具体相关性分析如下.肺癌是严重威胁人体生命健康的恶性肿瘤之一,流行病学研究表明85%的肺癌发病是由长期吸烟引起的,此外,引起肺癌的其他因素还包括遗传,职业,电离辐射,空气污染等[39].Du等人[40]发现lncRNA CDKN2B-AS1通过调节p53信号通路介导了特发性肺纤维化患者肺癌的发生.Jun等人[41]发现,lncRNA UCA1可以调节肺癌细胞的增殖、侵袭能力并诱导细胞凋亡,并推测UCA1可能成为治疗肺癌的重要靶点,而lncRNA GAS5在肺癌的发生发展中具有抑制作用[7].

上述分析结果表明,MRNMFLDA方法对lncRNA-疾病关系具有可靠的预测能力.同时MRNMFLDA方法预测方法在未来的lncRNA-疾病关系研究和实验验证中具有巨大的潜力.

4.4 讨论

lncRNA在疾病的发生过程中起着重要作用,因此研究lncRNA与疾病的关系是非常有必要的.本文提出了一种新的流形正则化非负矩阵分解方法来预测lncRNA与疾病的关系.首先,本文采用的相似性网络融合方法不仅考虑了两种数据源的有效融合,而且有效缓解了数据稀疏性的问题.然后,本文基于流形正则化思想将疾病网络融合相似性和lncRNA网络融合相似性这两个相似性网络正则化项与标签加权矩阵合并到标准NMF框架中,充分考虑了数据内部的几何结构的联系,既防止了过拟合问题并显着提高了预测性能.进一步的LOOCV和5-fold-CV实验验证以及肺癌,宫颈癌、骨肉瘤3种疾病的案例分析证明了MRNMFLDA预测方法对lncRNA-疾病关系具有可靠的预测能力.更重要的是,该方法也降低了研究者们研究不同疾病的致病基因的研究成本.总之,结果表明,MRNMFLDA在探索lncRNA-疾病潜在的关系中发挥积极作用.

下一步的更深入的研究工作中,将考虑改进相似性网络融合方法,提出更好的优化正则化约束方案来提高方法的预测能力.