基于强化学习的交通情景问题决策优化

罗飞，白梦伟

（华东理工大学计算机科学与工程系，上海 200237）

0 引言

随着汽车行业的快速发展和城市出行人口的增多，交通情景问题复杂度越来越高，如何在复杂的交通情景下作出决策成为一个热点问题［1］。交通情景问题涉及多种领域，如道路改建、拥堵预测、路径规划、信号灯控制等。其中，不良的路径规划和信号灯控制决策可能导致长时间的交通延迟、车辆拥堵、额外的车辆燃油消耗和环境污染，受到了许多研究人员的关注。

面对路径规划问题，目前的解决思路包括基于索引的A*（Index Based A Star，IBAS）算法［2］、Floyd-A*算法［3］、基于动态图的K条最短路径（KShortest Paths in Dynamic Graphs，KSP-DG）［4］算法等。其中，IBAS 算法对传统的A*算法［5］进行了改进，为每个顶点构造了三个索引，以处理未知顶点坐标对路径规划的影响，然而难以满足更复杂的路径规划需求；Floyd-A*算法分为基于A*算法的行程查找器和基于Floyd 算法［6］的成本估计器两部分，用于处理最短时间的行程规划问题，然而计算效率有待提高；KSP-DG 算法改进了K条最短路径（KShortest Paths，KSP）算法［7］，将图划分为多个子图进行处理，使算法可部署于分布式环境，然而在未知条件下的表现能力有限［8］。另外，由于针对路径规划问题设计的算法难以迁移到其他优化问题中，应用范围具有局限性。

面对交通信号灯控制决策问题，目前常用的决策方法包括自组织的交通灯（Self-Organizing Traffic Lights，SOTL）算法［9］、最大压力算法［10］等。其中，SOTL 算法在得知当前道路上红灯车辆等待数量、绿灯车辆行驶数量信息后，基于最小相位时间、相位改变阈值等超参数，选择后续的交通信号相位动作；该算法依赖的超参数较多，经验性的参数取值容易导致最终结果的不确定性，且无法适应动态环境。最大压力算法根据当前的交通环境计算各个交通信号相位的车流压力，之后选择具有最大压力的相位作为后续的动作；然而该算法本质上属于贪心算法，在求解过程中容易陷入局部最优，最终的方案具有一定的局限性。

针对以上算法在路径规划问题、交通信号灯控制问题中表现能力有限、需要经验知识等问题，近年来，研究者提出利用强化学习算法来解决上述问题。其中，文献［11］使用Q-Learning 算法解决交通信号灯控制问题，但是需要合理设计马尔可夫决策过程（Markov Decision Process，MDP），以提高算法的表现能力；文献［8］基于Dyna 算法［12］，利用Sarsa 算法在行为选择上较为保守的特性，减少了路径规划问题中车辆的碰撞次数，但实验基于静态交通环境，未讨论动态变化情况下的交通情景问题决策；文献［13-15］使用深度强化学习算法，分别基于改进深度Q 网络的NDQN（improved Deep Q Network）算法、多智能体的自适应交通信号控制器集成网络（Multi-Agent Reinforcement Learning for Integrated Network of Adaptive Traffic Signal Controllers，MARLIN-ATSC）算法、最大压力的MPLight 算法，解决交通信号灯控制问题；然而，深度强化学习算法在解决交通信号灯控制问题上的计算时间成本较高、建模复杂，需要通过大量的样本学习，无法快速得到解决方案。

深度强化学习算法存在计算速度慢和建模复杂的问题，而传统强化学习算法基于表格形式的价值估计［16］，在建模和计算速度上具有优势，但由于传统强化学习算法与环境之间存在交互成本、动作选择策略、收敛速度和精度等问题，需要改进。已有的改进算法中，快速Q 学习（Speedy QLearning，SQL）［17］、连续过松弛Q 学习（Successive Over-Relaxation Q-Learning，SOR Q-Learning）［18］、广义快速Q 学习（Generalized SQL，GSQL）算法［19］没有考虑到交互成本和动作选择策略；Dyna-Q 算法建立了环境模型，通过集成学习、规划与交互，降低了交互成本［12］，但仍然使用贪婪策略作为动作选择方式，且Q函数的更新仍然采用传统的Q-Learning算法方式，具有改进空间。

本文将Dyna-Q 算法中环境模型设计为经验池，并针对动作选择构建一种直接策略，基于GSQL 算法提出一种结合了经验池技术和直接策略的改进强化学习算法——GSQLDSEP（Generalized Speedy Q-Learning with Direct Strategy and Experience Pool），以加快算法的收敛和提高收敛精度；之后将GSQL-DSEP 算法应用到出租车司机搭乘问题中，缩短搭乘决策的路径长度；随后通过城市交通仿真（Simulation of Urban Mobility，SUMO）软件仿真交通信号灯系统，构建出离散环境下的马尔可夫决策过程，并应用GSQL-DSEP 算法，减少交通信号灯系统中车辆的整体等待时间。

1 强化学习算法优化

1.1 强化学习

强化学习的执行过程是智能体与环境不断交互的过程，用于解决马尔可夫决策过程建模的问题。一般情况下，马尔可夫决策过程包含了S、A、R、P 在内的四个要素。其中，S 为智能体的状态表示，A 为智能体的行为表示，R 为环境的奖励概率函数表示，P 为环境的状态转移概率函数表示。强化学习算法的智能体最直接的学习目标是在与环境不断交互中产生最大的累积奖励。智能体和环境的交互如图1所示。

图1 智能体和环境的交互示意图Fig.1 Schematic diagram of interaction between agent and environment

智能体和环境的交互任务可以分为无限时长交互和回合式交互，而无限时长交互可转换为最大时长为T的回合式交互以便统一表示。在一个时间周期T内，智能体在时刻t获取到奖励rt后，该时刻下智能体未来能够获取到的奖励和Gt如式（1）所示。其中，由于尚未得到的奖励常常具有不确定性，且远离时刻t时不确定性更大，因此式（1）一般添加衰减因子γ，以逐次降低未来奖励的权重。

智能体在时刻t作出的行为选择倾向于能够获取最大的Gt。定义智能体在状态s和行为a下，获得的未来奖励和的期望为Qπ，则最终得到的贝尔曼公式如式（2）所示，对应的贝尔曼最优公式如式（3）所示，其中p为状态转移概率函数，π为策略选择概率函数。通过贝尔曼最优公式，可以得到强化学习算法中Q-Learning 的更新公式如式（4）所示。

其中：α(s，a)为学习率；r为奖励值；s′为下一个状态；a′为下一个行为。

1.2 本文算法GSQL-DSEP

本文提出一种利用直接策略和经验池技术的广义快速Q 学习算法（GSQL-DSEP）。在该算法中，利用优化的贝尔曼公式和快速Q 学习以加快算法收敛；引入经验池技术提高智能体交互经验的利用率；使用直接策略提高行为选择的均匀性。GSQL-DSEP 算法描述如下。

1.2.1 基于优化贝尔曼公式的快速Q学习机制

Q-Learning 算法的一种改进方法是使用两个连续的“行为-价值”函数［17］，本文借鉴该思想以获得比标准Q-Learning算法更快的收敛速度。定义在时刻k的Q函数为Qk，使用连续的“行为--价值”函数的快速Q 学习算法在更新过程中使用更新公式（5）～（6）。其中式（6）表示更新过程的最终规则，使用时依赖于式（5）的“行为-价值”函数。

Q-Learning 算法的另一种改进方法是使用优化的贝尔曼公式［18］，通过添加松弛量得到的Q函数更新公式如式（7）所示：

其中：参数w为松弛量，取值范围在0 到w*之间。w*的计算方式如式（8）所示：

将优化的贝尔曼公式和连续的“行为-价值”函数相结合，可进一步提高Q-Learning 算法的收敛效果［19］。本文借鉴该思想，最终GSQL-DSEP 算法使用的Q函数更新公式如式（9）～（10）所示（算法1 中第7）行和第12）行使用该Q函数更新方法）：

其中：Qk+1表示k时刻需要计算的Q函数；Qk和Qk-1分别对应前一时刻的Q′和前二时刻的Q"。

1.2.2 经验池技术

Dyna-Q 算法提出了学习、规划和交互进行集成的思想［12］，本文借鉴该思想，设计了经验池用于规划与交互。经验池的表示使用数组形式，初始化时即分配完整存储空间，并计算空间使用量和存储位置索引。存储过程在智能体作出决策并获得下一个状态后，将该次所经历的状态、行为、下一个状态和奖励进行打包，存储到数组中，然后更新存储位置索引和空间使用量。采样过程对应模拟经验的生成，依据空间最大使用量，生成随机索引从而获取对应的经验信息。

基于经验池技术的GSQL-DSEP 算法结构如图2 所示。从交互环境到实际经验，然后进行Q函数的更新，对应算法1中第5）～8）行；从实际经验利用经验池进行经验存储操作，然后从经验池中采样获取模拟经验，最后使用模拟经验进行Q 函数的更新，对应于算法1 中的第9）～13）行。

图2 GSQL-DSEP算法结构Fig.2 Structure of GSQL-DSEP algorithm

1.2.3 直接策略

通常强化学习算法采用贪婪策略用于行为选择，导致动作空间过大时，指定状态下的行为选择不够均匀，难以更新所有动作的价值估计，最终算法的收敛效果不够稳定。

因此本文构建一种直接策略，如以下定义所示，并将其应用到算法1 中；算法1 中的第5）行未使用贪婪策略，而是根据Q函数使用直接策略，以提升算法行为选择的均匀性。

直接策略：在MDP 模型中奖励通常为负值的情况下，初始化后的函数价值估计全为0 时，可直接选取当前状态下最大价值的行为，替代贪婪策略。

使用直接策略后，由于初始化后的Q函数价值估计全为0，则每次算法更新后，动作的价值估计都会变小，使算法下次选择其他动作，而动作估计最终会收敛到稳定值，策略变为确定性的行为选取。

1.3 强化学习算法性能分析

1.3.1 算法测试环境

本文使用Mdptoolbox 的Python 工具包作为工具，在Windows10 操作系统下的Python3.7 开发环境中进行了算法性能测试。Mdptoolbox 工具包提供了Q-Learning、策略迭代、值迭代等强化学习传统算法，并可以生成随机的马尔可夫决策过程场景，便于实现算法的对比与验证。随机的马尔可夫决策过程场景在建立时，设定马尔可夫决策过程中的状态个数和动作个数后，会获得一个随机的奖励函数矩阵，以及一个随机的状态转移概率函数矩阵。其中，奖励函数矩阵的取值为-1～+1，为了便于GSQL-DSEP 算法在该环境中的应用，本文将该奖励函数矩阵整体减1，使得取值为-2～0。Mdptoolbox 生成的随机场景将具体问题进行了抽象和归纳，相较于特定应用场景而言更具有代表性。本文以Mdptoolbox 生成的随机场景为算法的测试和对比环境，以增强实验对比结果的准确性和可靠性。

1.3.2 评估比对方法

本文对比了Q-Learning算法、SQL算法、GSQL算法、Dyna-Q 算法和改进的GSQL-DSEP 算法。考虑到算法对比的公平性，本文参考了GSQL 算法在实验中选取的超参数，同样选取状态个数为10，动作个数为5，每个回合长度为100，执行回合数为1 000，算法的选择折扣因子γ为0.6，松弛量w为w*；考虑到算法对比的准确性，本文的评估对比实验进行了100 次，以最优价值和Q函数计算得到估计价值的欧氏距离平均值作为度量方式。假定时刻t下共有状态个数为N，使用q表示测试算法得到的价值估计函数，使用v*表示最优的价值估计函数，则时刻t的测试算法误差可以表示为：

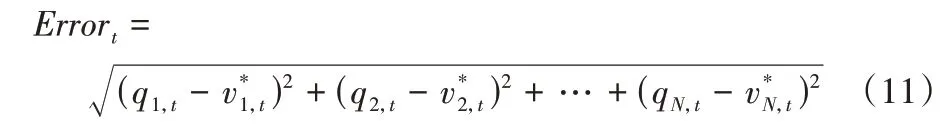
假定第i次实验下的时刻t得到的误差为，并假定100 次实验在时刻t得到的误差平均值为，则本文最终使用均方误差度量方式如式（12）所示：

1.3.3 实验结果与分析

实验中，本文提出的GSQL-DSEP 算法需要使用经验池，因此首先对经验池的参数选取进行了实验。在经验池大小为20 000，选取经验池采样数量为1、3、5 时的GSQL-DSEP 算法结果如图3 所示；在采样数量为3，经验池大小为20、200、2 000、20 000时的GSQL-DSEP 算法结果如图4所示。从图3～4 可以看出：采样数量对GSQL-DSEP 算法的影响较大，而经验池大小对GSQL-DSEP 算法影响较小。由于采样数量的增加额外增加了计算成本，而经验池大小在该测试中体现出的算法性能差异不明显，综合考虑适用性、计算成本和环境的差异性可能对算法产生的影响等，在后续不同的实验环境中，仍需进行不同参数下的实验和具体参数的选定。

图3 不同采样数量下GSQL-DSEP算法表现Fig.3 Performance of GSQL-DSEP algorithm under different sampling numbers

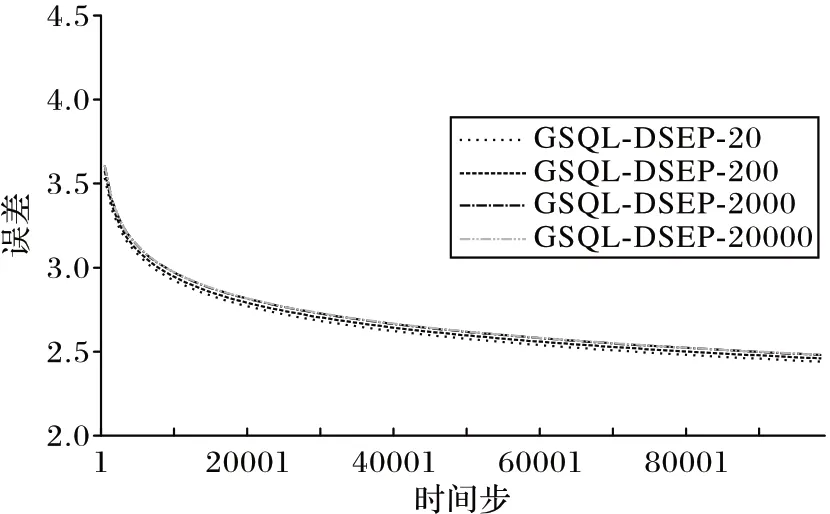
图4 不同经验池大小下GSQL-DSEP算法表现Fig.4 Performance of GSQL-DSEP algorithm under different experience pool sizes

图5 为Q-Learning 算法、SQL 算法、GSQL 算法、Dyna-Q 算法和提出的GSQL-DSEP 算法的均方误差对比结果。其中，Dyna-Q 算法和GSQL-DSEP 算法的经验池大小为20 000，经验池采样数量为3。从图5 可以看出，GSQL-DSEP 算法与最优值之间的均方误差更小。其中，各算法的均方误差MSEalg（alg∈｛GSQL-DSEP，Q-Learning，SQL，GSQL，Dyna-Q｝）分别为MSEGSQL-DSEP=2.48、MSEQ-Learning=4.29、MSESQL=4.27、MSEGSQL=4.09、MSEDyna-Q=3.05。根据式（13），相较于Q-Learning、SQL、GSQL、Dyna-Q 算法，GSQL-DSEP 算法的均方误差值分别下降了42.2%、41.9%、39.4%、18.7%。实验结果表明，GSQL-DSEP 算法优于对比的其他强化学习算法，可提升收敛精度。

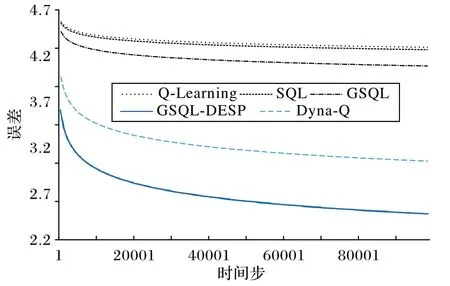
图5 不同强化学习算法的均方误差对比Fig.5 Mean square error comparison of different reinforcement learning algorithms

2 交通情景问题决策优化

将GSQL-DSEP 算法应用在交通情景中，用于解决出租车司机搭乘决策优化问题和交通信号灯控制决策优化问题。

2.1 出租车司机搭乘决策优化

出租车司机搭乘决策问题［20］的目标是在交通环境中提供一套搭乘决策，最小化行驶路径决策长度。目前，该问题由OpenAI 组织进行了封装和重新实现，以gym 工具包作为该问题的调用接口。如图6 为出租车司机搭乘环境的示意图。其中，出租车使用半圆表示，且在5 × 5 网格中的初始位置随机；RGBY（对应红色、绿色、蓝色、黄色）四个位置随机存放了乘客的等待位置和目的地；环境中同时也存在一些墙壁障碍。出租车需要在和环境的交互过程中，学习到载客和卸客的路径规划和决策。

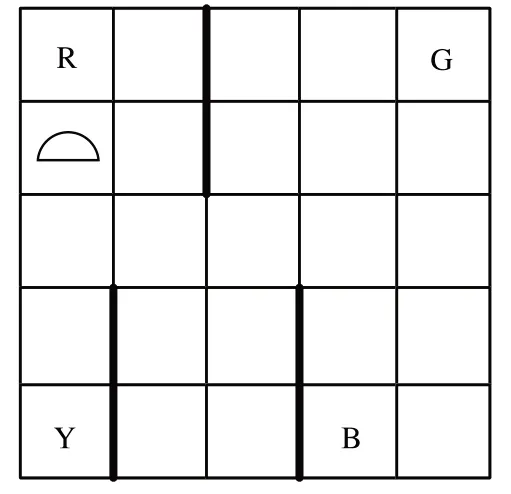
图6 出租车司机的搭乘环境Fig.6 Driving environment for taxi drivers

为了应用强化学习策略解决出租车司机搭乘决策问题，需要设定相应的状态表示、动作表示、奖励函数和强化学习算法的超参数。在状态表示的设定上，由于该环境空间大小为25，且有5 个可能的乘客位置（包括乘客在出租车内）、4 个可能的目的地，因此最终的状态个数为500；动作空间、奖励函数和强化学习超参数的设定分别如表1～3 所示。

表1 出租车动作空间定义Tab.1 Definition of taxi action space

表2 出租车奖励函数定义Tab.2 Definition of taxi reward function

表3 出租车超参数设定Tab.3 Hyperparameter setting for taxis

由于迭代过程累积奖励随机性较大，因此本文取每20次迭代的平均奖励值作为评价，评估长度为30，并重复10 次实验求取平均值作为最终的评价指标。GSQL-DSEP 算法存在经验池大小和经验池采样数量两个超参数，在出租车司机搭乘决策问题中，不同的超参数对该算法的影响如图7～8 所示。图7 显示了在经验池采样数量为3 的情况下，经验池大小为20、200、2 000、20 000 时的平均路径长度变化。从图7可以看出，不同的经验池大小对前期的收敛速度具有一定影响，更大的经验池对收敛速度具有部分提升作用，但对最终的收敛结果影响不大。图8 显示了在经验池大小为20 000的情况下，经验池采样数量为1、3、5 时的平均路径长度变化。从图8 可以看出，采样数量多则收敛速度变快，但对最终的收敛结果同样影响不大，且更多的采样数量会引入额外的计算开销。根据上述实验结果，在后续的对比实验中，GSQL-DSEP 算法经验性地选取经验池大小为20 000、采样数量为3。

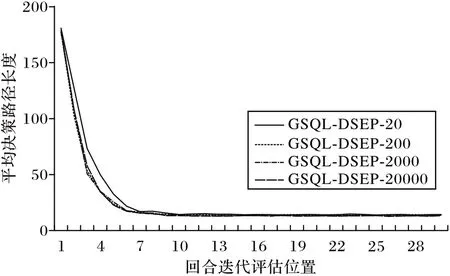
图7 经验池大小对决策路径长度的影响Fig.7 Influence of experience pool sizes on decision path length

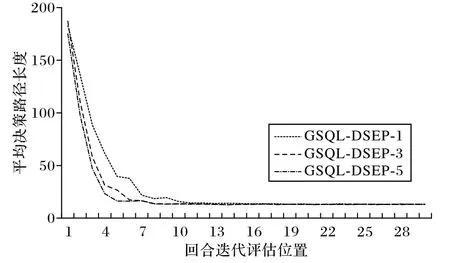
图8 采样数量对决策路径长度的影响Fig.8 Influence of sampling numbers on decision path length

将传统强化学习算法、其他改进算法以及本文提出的GSQL-DSEP 算法应用到该环境中，最终结果如图9～10 所示，相应算法的平均决策路径长度为LENalg（alg∈｛GSQL-DSEP，Q-Learning，SQL，GSQL，Dyna-Q｝）。最终结果表明，在面向最优路径决策的选取过程中，相较于Q-Learning、SQL、GSQL、Dyna-Q 算法，GSQL-DSEP 算法得到的累积奖励更高；各算法所对应的决策路径长度分别为：LENGSQL-DSEP=13.345、LENQ-Learning=16.62，LENSQL=16.3，LENGSQL=16.16，LENDyna-Q=16.315，即GSQL-DSEP 所对应的决策路径最短。根据式（14），相较于Q-Learning、SQL、GSQL、Dyna-Q 算法，GSQLDSEP 算法的平均路径长度分别缩短了约19.7%、18.1%、17.4%、18.2%。结果表明，相较于传统强化学习算法，GSQL-DSEP 算法能够缩短出租车司机搭乘问题中的决策路径长度。

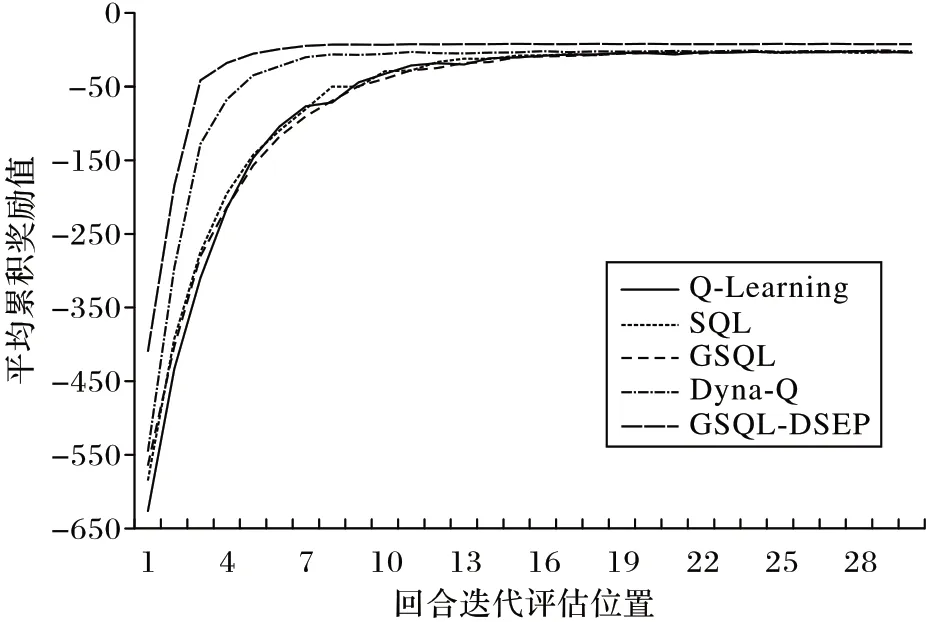
图9 不同算法在出租车路径规划中的累积奖励对比Fig.9 Comparison of cumulative reward among different algorithms in taxi path planning

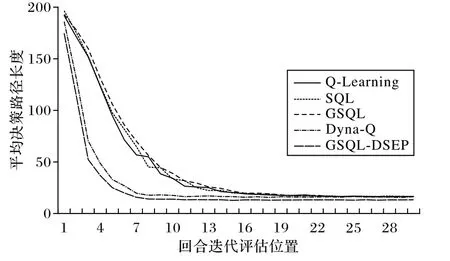
图10 不同算法决策路径长度对比Fig.10 Comparison of decision path length amongdifferent algorithms

2.2 交通信号灯控制决策优化

交通信号灯控制决策优化，能够提升现有交通网络的利用效率，减少交通系统中车辆的整体等待时间。本节首先在交通信号控制仿真软件SUMO（Simulation of Urban MObility）中建立十字路口的交通信号灯控制MDP 模型，然后将强化学习算法应用在交通信号灯控制问题上，以减少车辆的等待时间。

2.2.1 交通信号灯控制MDP模型

本文首先基于点、边和连接的三个配置文件生成基本的路况环境，然后使用netedit 软件修改路径信息，得到的仿真环境如图11 所示，其中涉及的超参数如表4 所示。

表4 交通环境参数Tab.4 Traffic environmental parameters

图11 信号灯控制环境Fig.11 Traffic light control environment

假定最快每1.2 秒从路口通行1 辆车，则路口最大的吞吐率为50 辆/分钟，因此在仿真环境中出现的车辆频率应小于50 辆/分钟。在车辆生成的过程中，考虑出现车辆的随机性，因此本文使用Python 脚本在每次重置环境后，对车辆信息重新生成。

在交通信号灯控制问题的动作表示上，通常情况下，右转信号灯为常绿状态，车辆可以直接向右通行，而左转和直行信号灯需要根据环境进行设置。当只有红灯和绿灯时，原始动作空间大小为（2 × 2）4，共256 个动作。然而，这些动作往往存在冲突问题，如某车道信号灯全绿时，则对应的左右车道信号灯应该为红色。基于以上思想，本文提出的交通信号灯控制动作表示如表5 所示，总动作个数减少到12，以每3个为一组，表示出右转、直行和左转的信号灯动作。其中G为绿灯，R 为红灯。在动作切换时，为了安全行驶，本文自动添加了黄灯作为过渡。

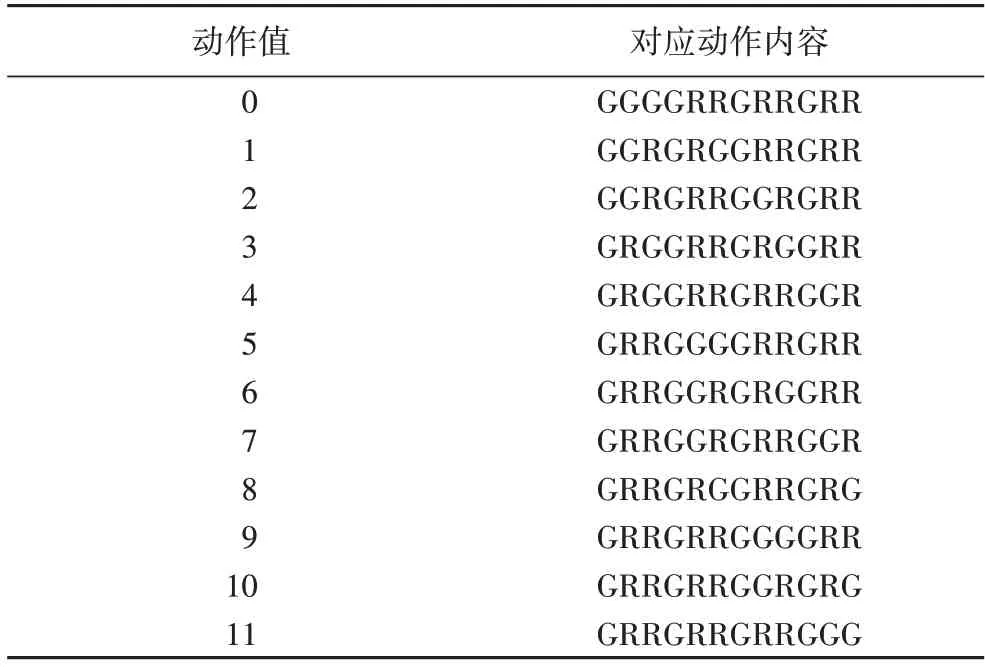
表5 信号灯动作空间定义Tab.5 Definition of traffic signal action space

在交通信号灯控制问题的状态表示上，针对每个车道上的车辆数量，设定车辆多、中、少三种状态。本文设定当车辆数量小于4，则车辆为少；若车辆不小于4 且小于9，则车辆数量适中；否则车辆数量为多。由于共有四个车道，本文使用三进制形式表示状态，最终的状态空间大小为81。

在交通信号灯控制问题的奖励函数上，应当包含最终要解决的问题，使最终车辆的整体等待时间最小，不出现车辆碰撞或急停现象，且交通灯信号改变频率不宜过快等。基于上述想法，本文使用的奖励函数定义如表6 所示，其中的K3在每个时间步为1，信号灯发生改变后K5为1，否则为0。

表6 信号灯控制的奖励函数定义Tab.6 Definition of reward function for traffic signal control

2.2.2 强化学习在交通信号灯控制中的应用

使用GSQL-DSEP 算法和Q-Learning算法、SQL算法、GSQL 算法、Dyna-Q 算法，对设计好的MDP 模型进行实验和仿真。在实验过程中，由于贪婪策略无法稳定收敛，因此本文在该情景中对比的所有强化学习算法都采用直接策略。在经验池大小的选取过程中，设定采样数量为3，然后选取不同的经验池大小进行测试。首先，设定经验池大小在200以上，算法最终累积奖励值变化较大，算法不够稳定；然后，设定经验池大小为20 时，算法最终收敛到的累积奖励值为-103.04，性能有待提高；随后，设定经验池大小为2 时，最终收敛到的累积奖励值为-27.392，得到的结果较为理想。由于SUMO 软件仿真和车辆生成过程的动态性，并根据文献［16］中8.3 节的分析，当环境变化后，在过大的经验池中，更旧的经验数据存储在经验池中被采样，影响了算法的更新过程，得到的结果具有局限性。基于上述实验结果，在经验池采样数量的选取过程中，设定经验池大小为2 的情况下选取不同的采样数量进行测试。当采样数量为1 时，最终收敛的累积奖励为-102.743；而采样数量为5 时，最终收敛的累积奖励为-27.292。在GSQL-DSEP 算法中，采样数量决定了使用模拟经验进行算法更新的次数，当使用可反映出环境动态变化的经验时，更多的更新次数有利于算法效果的进一步提升，但计算量更大。综合考虑算法效果和计算成本，后续选用的经验池大小为2，采样数量为3。

在面向最优决策过程中，最终得到的每回合累积奖励如表7 所示，智能体决策下的车辆的总等待时间TIMEalg（其中，alg∈｛GSQL-DSEP，Q-Learning，SQL，GSQL，Dyna-Q｝）如表8 所示。根据式（15），相较于Q-Learning、SQL、GSQL、Dyna-Q 算法，GSQL-DSEP 算法的车辆总等待时间TIMEGSQL-DSEP分别减少了51.5%、51.5%、0%、3.4%。实验结果表明，相较于其他强化学习算法，应用GSQL-DSEP 算法能够获取最大的累积奖励值，最终得出的车辆总等待时间具有更大优势。

表7 不同算法得到的信号灯控制最终累积奖励Tab.7 Final cumulative rewards of traffic signal control obtained by different algorithms

表8 不同算法得到的车辆总等待时间单位：sTab.8 Total waiting time of vehicles obtained by different algorithms unit：s

3 结语

强化学习算法可以解决交通情景下的出租车司机搭乘问题和交通信号灯控制问题。在算法方面，本文对强化学习算法进行了优化，结合了经验池技术和直接策略提出了一种新的广义快速Q 学习算法GSQL-DSEP，从算法对比实验可以看出，本文提出的GSQL-DSEP 算法相较于其他对比的强化学习算法提高了收敛精度。在应用方面，GSQL-DSEP 算法在解决出租车司机搭乘决策优化问题时，缩短了搭乘决策的路径长度；在解决交通信号灯控制优化问题时，可获得更高的累积奖励，得出的交通系统中车辆总等待时间更具优势。然而，GSQL-DSEP 算法仍然存在一些局限性。首先，如果应用环境发生较大变化，则从经验池中采样的经验难以模拟出变化后的环境信息，进而导致后续收敛性不够稳定；其次，更多的采样数量及其对应的更新次数会引入额外的计算开销，且算法的提升效果有限；最后，由于采用直接策略，应用场景应合理设计奖励函数，保证在该算法下智能体行为选择策略的探索性。