碳纤维角联织机经纱张力的H∞网络化控制
夏鹏飞, 刘薇,2*
(1.天津工业大学机械工程学院, 天津 300380; 2.天津工业大学天津市现代机电装备技术重点实验室, 天津 300387)
碳纤维作为一种基础性原材料被广泛应用于航空航天、新能源汽车等高尖端领域[1],碳纤维角联织机的关键控制技术研究对于碳纤维织物的性能提升具有重要意义[2]。碳纤维角联织机是一种含有多子系统分散协同工作的复杂装备,其控制系统为分布式、网络化的在整个控制期间,信号是通过CANbus网络传输的.整个张力控制系统的稳定性会不可避免受到时延、数据丢包等网络特性干扰。
关于织机张力系统的控制问题,文献[3]针对多电机卷绕系统中存在的多因素非线性耦合、外部扰动、内部参数不确定性,提出了一种分散H∞鲁棒控制器,仿真结果表明:所提出的控制器可较好地抑制外部扰动和卷取子系统间耦合作用产生的张力波动,大大提高了卷绕系统的张力控制性能。文献[4]针对双辊卷绕张力系统设计了一种混合摆动辊,并采用比例、积分(proportional integral,PI)控制器控制驱动辊的运转速度,实现了张力系统的稳定。文献[5]分析了织机卷取机构的力学模型,利用神经网络比例、积分和微分(proportional integral derivative,PID)控制器实现了卷取机构的恒张力控制,具有较高的控制精度。然而,现有的研究在进行张力控制器的设计时往往忽略了网络因素对其稳定性产生的影响。
近年来,中外学者对网络化控制系统开展了大量理论研究,并取得了一定的成果[6]。文献[7]针对离散网络化控制系统中由于数据包丢失、网络时延而导致的系统控制稳定性能变差的问题,设计了一种切换状态反馈控制器,并通过仿真表明所设计的控制器是有效的。文献[8]针对一类具有执行器和传感器故障的网络控制系统,提出了一种基于系统估计信息的快速高阶滑模控制器,验证了其对系统故障和外部扰动的鲁棒性。网络化控制系统也被广泛应用于许多领域,文献[9]提出了一种基于观测器的无人艇航向控制器,实现了网络环境下无人水面艇的航向精确控制。为了抑制分布式网络化电力系统中存在的低频振荡现象,文献[10]提出了一种T-S(Tkagi-Sugneo)模糊网络化控制策略,实现了系统的稳定性;文献[11]提出了一种H∞输出反馈耦合控制策略,实现了车与车相耦合的智能车网络化控制系统的稳定控制。然而现有的文献鲜有涉及纺织工业中网络化控制系统的研究。
因此,研究将先进的网络化控制理论应用于碳纤维角联织机的经纱张力控制,解决网络干扰等不确定因素给张力控制系统带来的消极影响,对网络化控制系统在纺织工业的实际应用有着重要意义。为此,首先给出带有非线性开口系统扰动的三自由度碳纤维角联织机系统状态方程,并将网络化控制思想应用于织机的张力控制上,在织机数学模型中引入时延、丢包等网络因素的影响,建立其网络化控制模型。然后,在该网络化控制模型的基础上,提出一种基于观测器的网络化最优H∞控制器,最终通过仿真实验验证该控制策略对经纱张力的控制效果。
1 碳纤维角联织机系统模型建立
碳纤维角联织机织造原理如图1所示,在织造过程中,经纱受开口、卷取、送经、引纬和打纬机构共同作用而产生形变,导致经纱张力在同一时间内受多个机构共同作用,其变化是一个复杂过程。
1.1 碳纤维经纱力学模型建立
碳纤维是一种黏弹性材料,其力学性能兼具弹性固体与粘性流体特征,表现在具有蠕变和应力松弛现象。实际工作中碳纤维纱线被要求恒张力拉紧,其松弛现象很微弱,因此尽管实际工作中碳纤维纱线不是理想的Kelvin模型,但却可以满足建模精度,为简化其动力学特性的分析,对碳纤维纱线的动力学分析中采用Kelvin模型。
Kelvin模型是由胡克弹簧和牛顿黏壶并联组成的,其结构如图2所示。Kelvin本构方程为
(1)
式(1)中:E为弹簧的弹性模量;η为黏壶的粘性系数;σ(t)为模型受到的应力;ε为形变;t为时间。

图1 碳纤维角联织机织造原理图Fig.1 Weaving principle diagram of carbon fiber diagonal loom
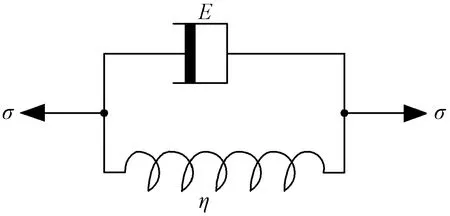
图2 Kelvin模型图Fig.2 Kelvin model diagram
根据Kelvin模型,可得经纱张力表达式为
(2)
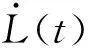
1.2 碳纤维角联织机系统动力学分析
送经系统的结构简图如图3所示,送经系统4个区域内张力T1、T2、T3、T4之间的关系可表示为
(3)
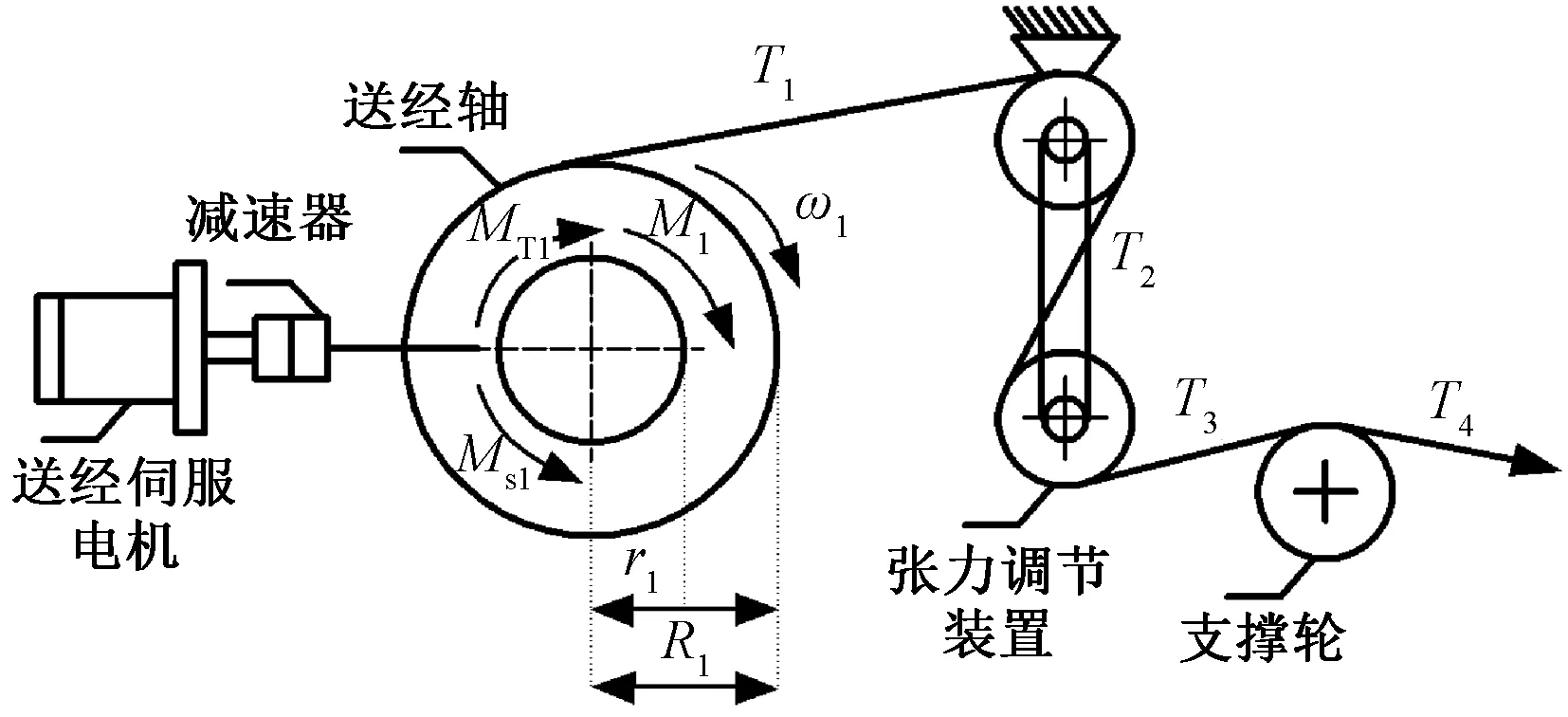
MT1、Ms1分别为电机的电磁转矩和转轴的摩擦转矩图3 送经系统结构示意图Fig.3 Structure diagram of let-off system
式(3)中:Jz1、Jz2、Jz3分别为回转辊、摆动辊、支撑轮的转动惯量;Rz1、Rz2、Rz3分别为回转辊、摆动辊、支撑轮的半径;Cz1、Cz2、Cz3分别为回转辊、摆动辊、支撑轮的黏性摩擦系数;ωz1、ωz2、ωz3分别为回转辊、摆动辊、支撑轮转动角速度。
送经轴等效半径的一阶微分可表示为
(4)
式(4)中:h为经纱厚度。
送经轴的转动惯量可表示为
(5)
式(5)中:Jm1为送经轴空载转动惯量;ρ为经纱的质量密度;b为经纱的宽度;r1为送经轴的空载半径。
根据送经轴和卷取辊的转动惯量和角动量之间关系,可得
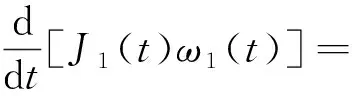
T1(t)R1(t)
(6)
式(6)中:MD1为送经电机的电磁转矩;i1为送经电机的减速比;CS1为送经轴的黏性摩擦系数。
卷取系统的结构简图如图4所示,卷取系统两个区域内的经纱张力T5、T6的关系可表示为
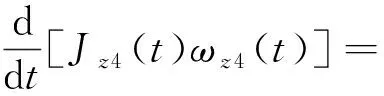
(7)
式(7)中:Jz4(t)为卷取系统支撑轮的转动惯量;Rz4为卷取系统支撑轮半径;Cz4为卷取系统支撑轮黏性摩擦系数;ωz4(t)为卷取系统支撑轮转动角速度。
卷取轴等效半径的一阶微分可表示为
(8)
卷取轴的转动惯量可表示为
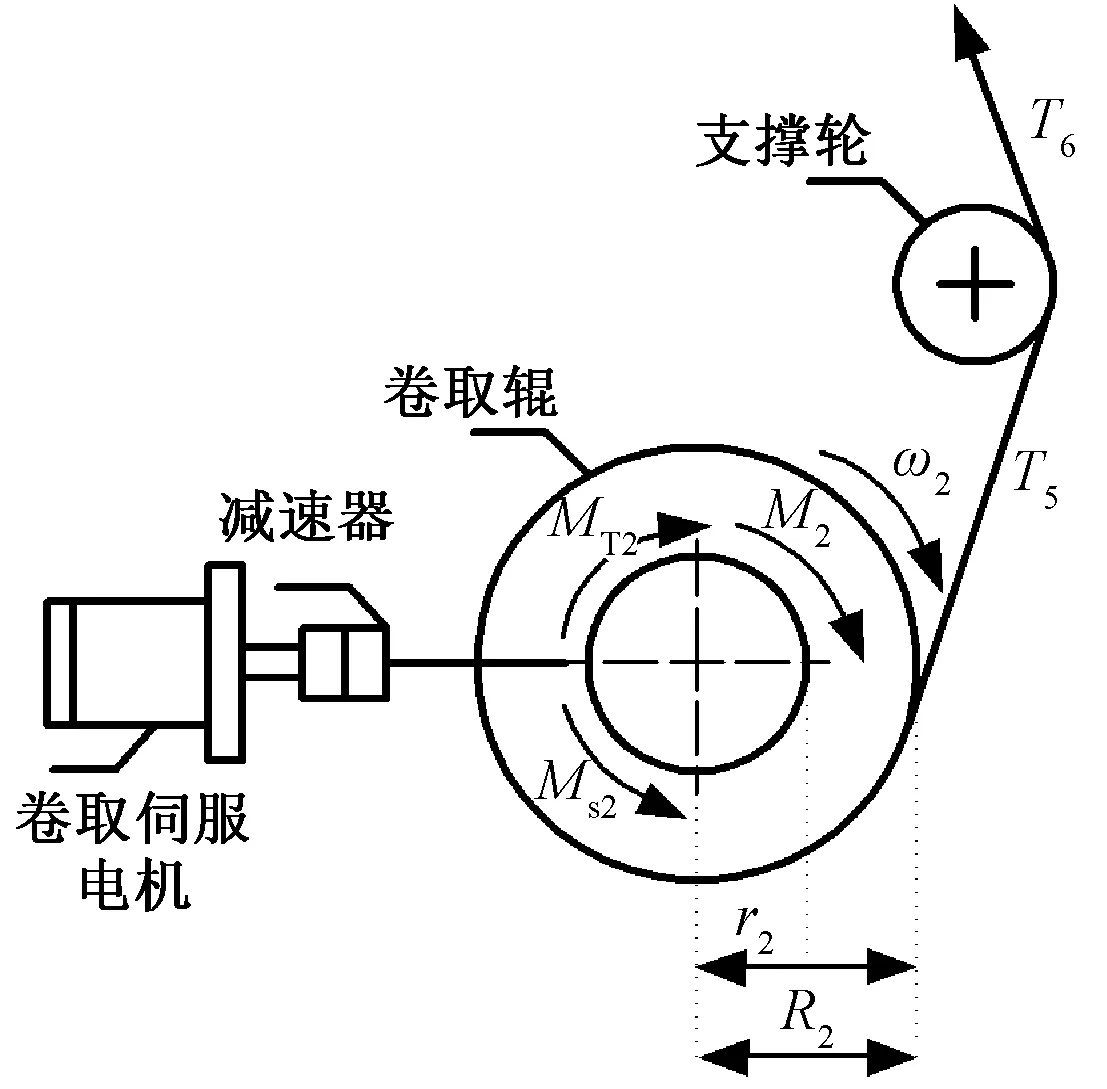
图4 卷取系统结构示意图Fig.4 Structure diagram of winding system
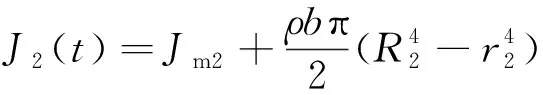
(9)
式(9)中:Jm2为卷取轴的空载转动惯量;b为经纱宽度;r2为卷取轴的空载半径。
根据卷取辊的转动惯量和角动量之间关系,可得
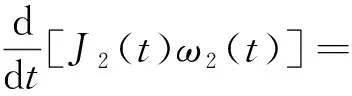
T5(t)R2(t)
(10)
式(10)中:MD2为卷取电机的电磁转矩;i2为卷取电机的减速比;CS2为卷曲辊的黏性摩擦系数。
实际工作过程中,影响织机纱线张力的因素很多,为了接下来更方便的研究,假设:各转辊和支撑轮均为理想质轻材料,摩擦系数非常小,且在织机运行过程中均为匀速运动。

基于假设可得
T1(t)=T2(t)=T3(t)=T4(t)=
T5(t)=T6(t)=T(t)
(11)
式(11)中:T为织机运行过程中的动态经纱张力,它在纱线任一处都是相等的。
联立式(7)、式(10)、式(11)得
(12)
式(12)中:Kw、Bw分别为经纱的弹性系数和阻尼系数。
进一步引入开口系统产生的经纱张力影响,根据文献[12]可知,碳纤维角联织机开口机构造成的经纱长度变化Lk(t)可表示为
Lk(t)=λsin2ζt
(13)
式(13)中:λ为织机梭口相关参数;ζ为碳纤维角联织主轴转动速度。
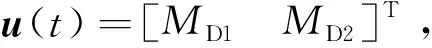
(14)
2 碳纤维角联织机网络化控制策略研究
碳纤维角联织机送经系统分为60套独立的送经装置,考虑到实施控制的成本和系统可靠性等因素,不能设置过多传感器,因此很难直接用状态反馈控制器进行控制,如果可以设计观测器估计实际状态,进而实现状态反馈,则更适合于实际的织机纱线张力控制。其次由于碳纤维角联织机运行过程中,系统同时存在不确定的开口系统扰动以及时延和丢包等网络干扰。H∞控制是把外部考虑在内的一种控制器,既保证了稳定性,又保证了外部扰动下的系统动态性能[13]。因此,将设计一种基于观测器的最优H∞控制器来实现织机系统在外部扰动和网络干扰下的恒张力控制。碳纤维角联织机工作原理图如图5所示。
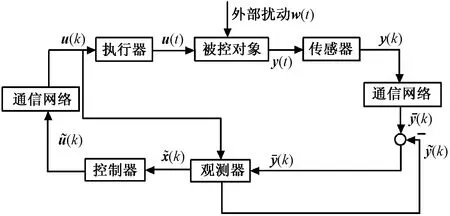
图5 碳纤维角联织机控制系统结构图Fig.5 Control system structure diagram of carbon fiber diagonal loom
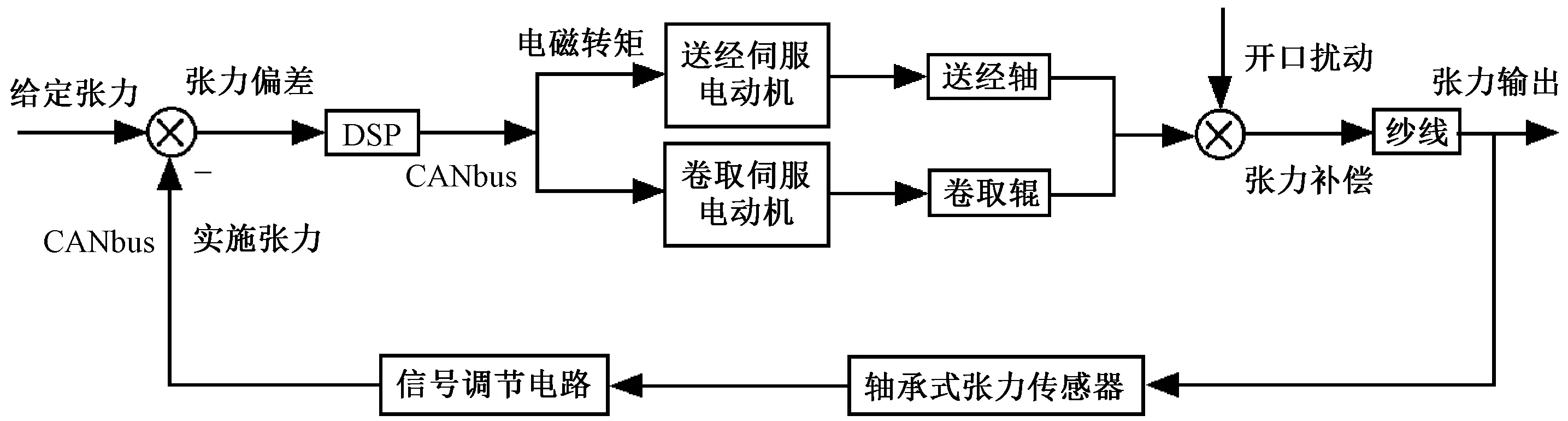
数字信号处理器(digital signal processing,DSP) ;CAN总线(controller area network bus,CANbus)图6 网络化控制系统结构示意图Fig.6 Structure diagram of networked control system
考虑CANbus网络环境下,织机的网络化控制系统结构如图6所示。
2.1 网络化控制系统模型建立
基于所提出的织机系统数学模型,考虑离散时间网络化模型为
(15)
式(15)中:x(k)∈Rn为系统状态;u(k)∈Rm为控制输入;y(k)∈Rp为测量输出;z(k)∈Rq为系统输出;w(k)∈Rr为外部扰动;A1、B1、E1、C1、D、E2、G为适当维数的系数矩阵。
考虑该离散网络化控制系统具有的观测器可表示为
(16)
考虑设计的状态反馈控制器可表示为
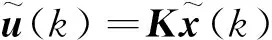
(17)
式(17)中:K为状态反馈控制器的增益矩阵。
进一步将通信网络中的时变时延和数据丢包现象代入式(19)、式(20)中,可将该时变时延的不确定性转化为系统系数矩阵的不确定性表示,丢包现象可用两个独立的伯努利随机分布表示[14],从而得到带有参数不确定性的离散时间系统状态方程网络化模型,可表示为
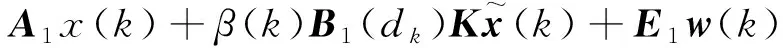
(18)
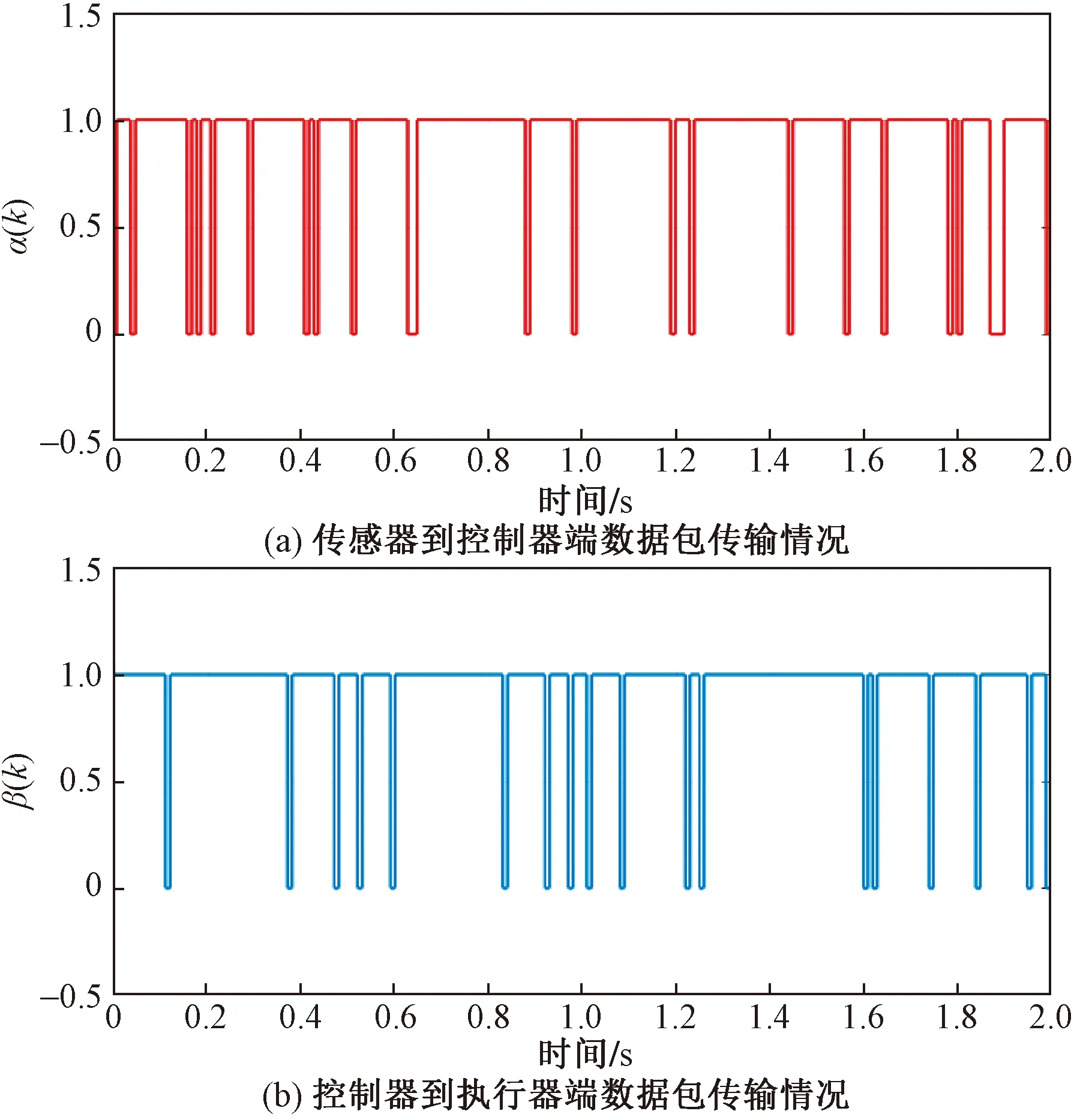
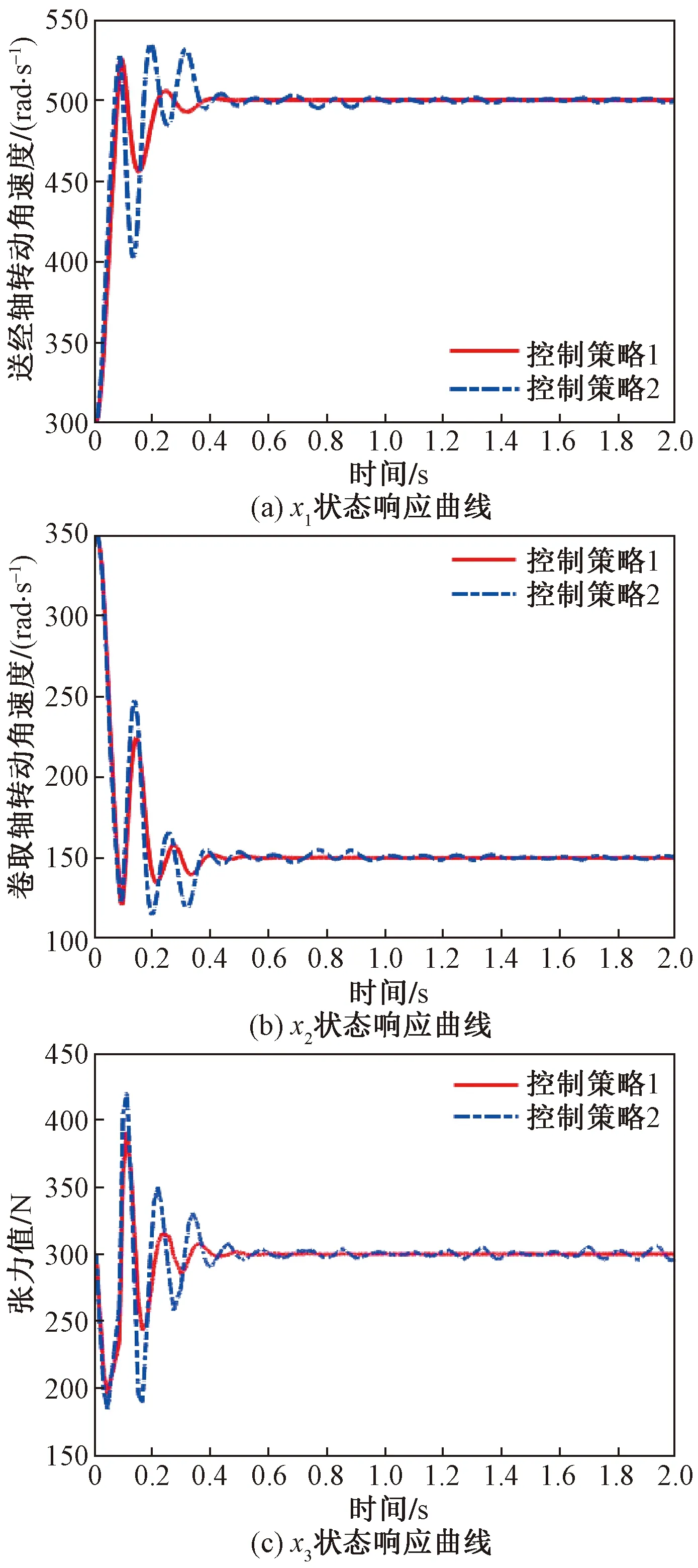
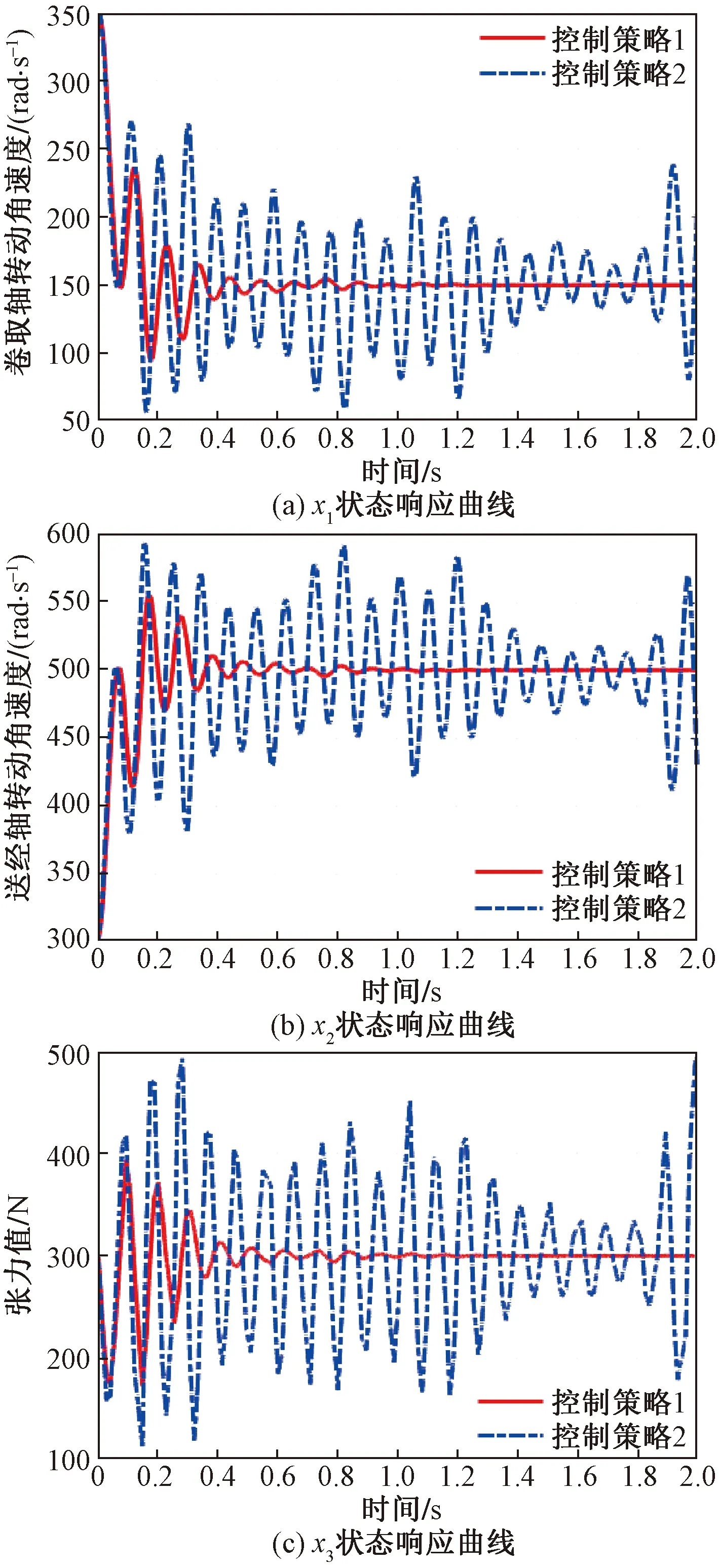
式(18)中:β(k)为伯努利随机分布序列,用来描述控制器端到执行器端的丢包现象;dk为控制器到执行器间的网络传输时变时延,且满足dm 考虑时延丢包现象后的有参数不确定性的离散时间系统的观测器,可表示为 (19) 式(19)中:α(k)为伯努利随机分布序列用来描述传感器端到控制器端的丢包现象;τk为传感器到控制器间的网络传输时变时延,且满足τm<τk<τM,其中τm和τM分别为τk的上、下限。 定义状态观测误差为 (20) (21) 针对式(21)所描述的闭环系统,研究系统满足均方指数稳定及H∞稳定的充分条件。为了进一步的证明,给出如下引理。 (22) 引理2对于给定的具有适当维数的矩阵Q=QT、Γ、Ψ、FFT<0。 Q+ΓFΨ+ΨTFTΓT<0 (23) 则式(23)成立的充要条件是存在一个正数ε>0使得式(24)成立。 Q+ε-1ΓΓT+εΨTΨ<0 (24) (25) 式(25)中:I为单位矩阵;γ为H∞性能指标。 证明:引入Lyapunov二次泛函: (26) 则可得 ΔV(k)=E{V(k+1)|η(k)}-V(k) (27) (28) 则可知当式(29)成立时,ΔVk≤0恒成立。 ηT(k)Λη(k)≤0 (29) 不妨令Λ<0,此时有 E{V(k+1)|η(k)}-V(k)=ηT(k)Λη(k) ≤-λmin(Λ)ηT(k)η(k) (30) 式(30)中:λmin为矩阵的最小特征值。 对于整数k=0,1,…,c,计算式(30)两侧的数学期望之和,可得 (31) 从而可得 (32) J=E[ΔV(k)]+E{zT(k)z(k)|ξ(k)}- γ2wT(k)w(k) =E{zT(k)z(k)|ξ(k)}-γ2wT(k)w(k)+ΔV(k) γ2wT(k)w(k)+ΔV(k) (33) 进一步,根据式(25),并运用引理1,可得 E[ΔV(k)]+E{zT(k)z(k)|ξ(k)}- γ2wT(k)w(k)≤0 (34) 即 (35) 则定理1得证。 由于实际求解不等式[式(25)]过程中,ΔB、ΔC、ΔD等非线性项均存在于增广后的系统矩阵参数,因此该不等式是不满足LMI条件的。 PS=I,QR=I (36) 证明:注意式(25)可重新表示为 (37) 由ΔB1、ΔC1、ΔD的结构可知,存在适当维数的常数矩阵H1、H2、M1、M2、M3,和未知的不确定矩阵F(dk)、F(τk)使得 (38) ΔC1=H2F(τk)M3 (39) 式中:F(dk)、F(τk)为未知不确定矩阵,且满足F(dk)FT(dk)≤I,F(τk)FT(τk)≤I。 将式(31)代入式(30)中可得 (40) 进而根据引理1可证定理2。由于式(36)中等式约束的存在,该矩阵不等式仍为非线性,因此该不等式矩阵仍非线性矩阵不等式(linear matrix inequality,LMI)可解。根据锥补线性化迭代(cone complementary linearisation,CCL)方法[16],采用一如下种凸优化方法来解决该非凸可行性问题,从而获得最优H∞控制器。算法步骤如下。 步骤1给定一个充分大的初始性能指标γ0,使得不等式存在LMI可行解。 步骤2令k= 0,分别对于矩阵P、Q、S、R、K、L寻找满足不等式的一组初始可行解并记为{P0、Q0、S0、R0、K0、L0}。 步骤3求解式(41)、式(42)所示的凸优化问题。 Minimize tr{PkS+PSk+QkR+QRk} (41) (42) 将所得出的解记为:{Pk+1、Qk+1、Sk+1、Rk+1、Kk+1、Lk+1}。 步骤4将所得到的解{Pk+1、Qk+1、Kk+1、Lk+1}代入定理2中,若满足,做如下最优解的赋值运算:{Popt、Qopt、Kopt、Lopt} = {Pk+1、Qk+1、Kk+1、Lk+1},并令γopt=γ-Δγ,其中Δγ为迭代算法中赋予性能指标的一个增量,返回步骤1;如不满足,且k 碳纤维经纱材料相关参数和碳纤维角联织机的系统相关参数分别如表1、表2所示。 将表1、表2参数代入式(14)中,可得系数矩阵参数为 CANbus网络因素参数选取如表3所示,设定系统采样周期为10 ms,可得离散系统参数为 表1 碳纤维经纱材料参数Table 1 Material parameters of carbon fiber warp 表2 碳纤维角联织机系统参数Table 2 Parameters of carbon fiber diagonal loom E2=[0.085 -0.032 0.079],G=[-0.028 -0.053]。 网络诱导时延d(k)和τ(k)的长度如图7所示,数据包传输情况如图8所示。 首先,对织机张力系统在理想环境下的工作进行仿真实验,在该仿真场景中,考虑织机CANbus网络的时延、丢包及系统的外部扰动均为0,通过本章中控制策略求解可得系统的H∞控制器增益矩阵和观测器的增益矩阵分别为 采用文献[3]控制策略所求的的控制器增益矩阵、观测器增益矩阵分别为 图7 CANbus通信网络中网络诱导时延的长度Fig.7 Length of network induced delay in CANbus communication network 表3 网络因素参数Table 3 Network factor parameters 图8 CANbus通信网络中数据包传输情况Fig.8 Data packet transmission in CANbus communication network 系统状态响应曲线如图9所示,可以看出,在该情况下,控制策略1和控制策略2均可使系统在0.3 s附近收敛到期望值,二者均实现对织机张力系统稳定控制,但控制策略1相较控制策略2状态抖动更小。 控制策略1为本文策略所求的控制器;控制策略2为文献[3] 中的控制策略图9 理想环境下织机张力系统状态响应曲线Fig.9 State response curve of loom tension system in ideal environment 第二组仿真实验中,只考虑系统中存在网络的随机时延与数据丢包干扰,通过本文策略求解可得系统的H∞控制器增益矩阵和观测器的增益矩阵分别为 采用文献[3]控制策略所求得系统的控制器增益矩阵和观测器增益矩阵分别为 织机张力系统状态响应曲线如图10所示。可以看出,控制策略1作用下系统的状态响应曲线仍可实现快速收敛,且准确跟踪期望状态,而控制策略2作用下系统的状态响应曲线受网络干扰影响,产生了明显抖动,无法对期望状态准确跟踪,始终存在跟踪误差。这是因为本文策略在设计过程中考虑了控制模型中的时延与丢包的不确定因素,从而对网络干扰产生了较好的鲁棒性。 图10 网络因素干扰下织机张力系统状态响应曲线Fig.10 State response curve of loom tension system under network factors disturbance 在最后一组仿真实验中,考虑织机在开口机构扰动及网络因素干扰同时存在的环境下工作,通过本文策略求解可得系统的H∞控制器增益矩阵和观测器的增益矩阵分别为 采用文献[3]控制策略所求得系统的控制器增益矩阵和观测器增益矩阵分别为 其系统状态响应曲线如图11所示。可以看出,控制策略1可在1.2 s附近实现状态收敛,且可在1.2 s之后无抖动的准确跟踪系统期望状态,而控制器2作用下的系统状态则无法实现收敛,系统状态始终存在较大抖动,且在后期系统状态有加剧发散的趋势。这验证了控制策略1对织机实际工作中存在的CANbus网络干扰及开口机构扰动均有较强的鲁棒性,可满足CANbus网络环境下的碳纤维角联织机的恒张力控制性能要求。 图11 CANbus网络环境下织机张力系统状态响应曲线Fig.11 State response curve of loom tension system in CANbus network environment 对CANbus通信网络环境下的碳纤维角联织机张力控制进行了深入研究。将网络化控制思想应用到了碳纤维角联织机的张力控制,建立了其网络化控制模型,不仅考虑了传感器到控制器的时延,同时也考虑了控制器到执行器的时延,将时变时延的不确定性转化为了系统参数矩阵的不确定性,并用Bernoulli随机分布序列描述了系统丢包过程,引入了系统的最优H∞性能指标,通过Lyapunov泛函和CCL迭代算法给出了H∞最优控制器及其观测器的设计方法。仿真结果表明,所提出的网络化最优H∞控制算法可实现张力系统状态的快速收敛并显著降低状态抖动,验证了其对碳纤维角联织机实际工作中存在的开口系统扰动、网络因素干扰具有良好的鲁棒性,说明该控制算法能够实现经纱恒张力控制。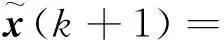

2.2 系统稳定性分析
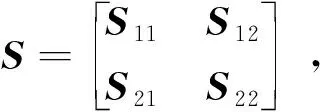
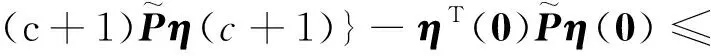
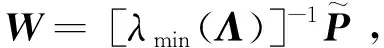
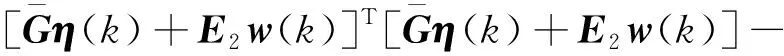

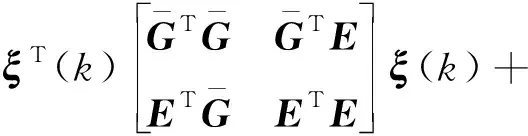

2.3 基于观测器的最优H∞控制器设计
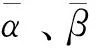
3 仿真分析
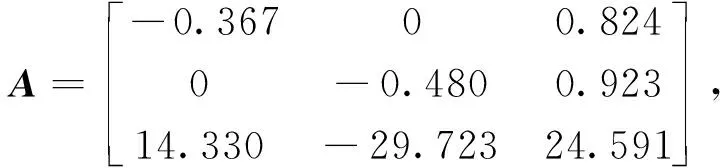








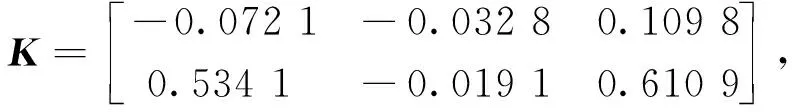
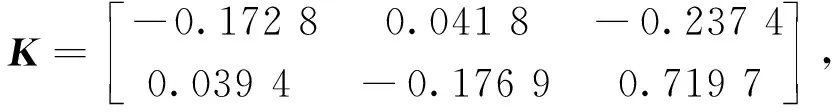
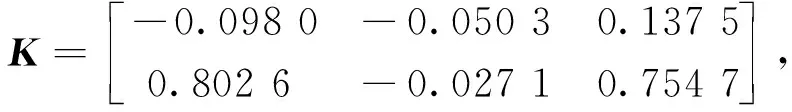
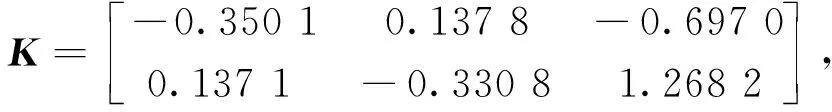
4 结论

