计及需求侧资源主动响应的含风电互联系统负荷频率控制

朱珂言， 王玮， 李雪寒

(华北电力大学控制与计算机工程学院， 北京 102206)

面对化石能源枯竭、环境污染、气候变化等人类社会面临的共同难题，大力开发和利用以风电为代表的新能源电力已成为国际社会的共识。截至2020年底，中国并网风电装机容量已突破2.8×108kW，连续12年稳居全球第一；2021年，中国提出了“2030碳达峰，2060年碳中和”的能源发展战略，“十四五”期间也将着力构建以新能源为主体的新型电力系统。然而，风电等新能源发电具有随机波动性、间歇性和反调峰等特性，其规模化并网将对电力系统的能量平衡、频率稳定等产生重大影响，严重威胁电能质量和系统稳定，这也是中国多年来饱受“弃风弃光”困扰的根本原因。

负荷频率控制作为维持电力系统稳定和电能质量的重要手段，其基本任务是调整系统的频率和区域联络线交换功率达到额定值(如50 Hz)。为改善负荷频率控制性能，中外学者重点围绕先进的调控理论方法和多能源互补开展了广泛研究。在控制理论方面，文献[1]提出了一种基于辅助反馈多区域互联电力系统负荷频率改进的比例积分 (proportional integral, PI)控制器切换面滑模控制器的设计方法,实现了对多区域互联电力系统负荷频率的优化控制；文献[2]提出了一种模糊控制方法，很好地抑制了频率跌落；文献[3]提出的模型预测控制器和文献[4]提出的自适应神经网络控制器对于处理系统频率偏差以及针对联络线功率发散有良好的控制效果；文献[5]提出了用改进的ACO算法优化模糊比例积分微分(proportional integral derivative, PID)控制器，改善了多区域互联电力系统的负荷频率控制性能。此外，基于差分进化算法的电网调频模糊PID控制[6]、深度强化学习[7-8]等智能控制方法[9]也大大改善了负荷频率控制性能。然而，随着波动性新能源在电网中渗透率的不断提高，系统的负荷频率控制仍面临巨大挑战[10]。

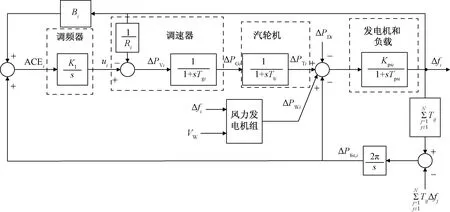
注：KI为PI控制器的积分参数；s为拉普拉斯算子；Vw为风速；ui为区域i的控制量；Kpsi为发电机和负载的增益；ΔPVi为调速器输入控制量； ΔPWi为区域i风电场的风功率；ΔPDi为负载需求变化扰动；Δfj为区域j的频差；Ri为调速器调速参数，Hz/p.u.；Tgi为调速器时间常数；Tti为 汽轮机时间常数；PGi为调速器输出指令，p.u.；ΔPGi为汽轮机输出功率的变化；ΔPTi为负载需求变化；Kpsi为发电机和负载的增益；Tpsi为发电机 和负载的时间常数；PI为负荷频率控制器；ΔPtie,i为区域i的联络线交换功率,p.u.；Bi为区域i的频率偏差常数；Δfi为区域i的频率偏差，Hz； Tij为区域之间的互联系数；ACEi为区域控制偏差，由Δfi和ΔPtie,i信号共同产生，作为负载频率控制器的输入，用于维持计划的系统频率和联络线功率图1 含风电互联系统频率控制模型Fig.1 Load Frequency control model of interconnected system with wind power

多能源互补可以有效平抑新能源电力随机波动性，加快系统的负荷频率响应。文献[11-12]研究了电解铝、电动汽车等资源的负荷响应特性，论证了灵活可调度资源对于提升系统频率稳定性的重要作用；文献[13-14]提出了基于荷电修正的储能电站参与负荷频率控制方法，大大改善了系统的调频性能，证明了大规模电池储能系统参与电力系统快速调频的显著优势。文献[15]引入需求响应参与度模型，采用分层优化的方法研究含分布式电源的配电网配置问题，验证了需求侧参与分布式电源并网能够有效改善能源消纳和削峰填谷效果。文献[16]将需求响应引入到含大规模风电的电力系统频率响应模型中，验证了需求响应在改善风电系统调频性能的重要作用；文献[17]提出了一种变频空调参与调频的模糊控制策略，取得了较好的振荡抑制效果。

现有研究表明，需求侧资源的灵活调节能力可以从本质上改善系统的负荷频率控制性能，但如何充分激发需求侧资源的主动响应能力并为高风电渗透率的新型电力系统提供支撑，仍亟待研究。为此，以空调类需求侧资源为例，建立了计及需求侧资源主动响应的含风电互联系统负荷频率控制模型；并综合考虑系统电源侧和负荷侧的双随机特性，设计了可最大化需求侧主动响应能力的线性自抗扰控制策略，可为大规模新能源电力并网提供有力支撑。

1 风电接入对系统负荷频率的影响分析

1.1 考虑风电不确定性的负荷频率控制模型

规模化新能源的接入使得传统电力系统逐渐演变为电源侧和负荷侧双随机的新型电力系统。维持各区域频率在额定值附近与控制联络线上的交换功率在协议规定数值的任务主要由自动发电控制系统完成[18]。现有多数风电机组运行过程中，采用是有功与电网频率间解耦控制，为了简化分析并方便控制器设计，将对互联电网频率影响较大的风电有功功率 作为随机项引入互联电网负荷频率控制模型中。

含风电互联系统负荷频率控制模型如图1所示。模型包括调频控制器，调速器，非再热汽轮机，发电机和负载。

1.2 不同风电渗透率下系统的频率特性

风机空气动力学模型中，风机的输入功率和风速、空气密度、桨距角等因素有关，单台风电机组的有功输出的随机性较强，主要原因在于风电机组多采用桨矩角控制跟踪最大功率输出，虽然存在风电场集群效应和风电机组叶轮自身的转动惯性，但影响电网频率变化的风功率主要集中在中、低频范围内。风电机组功率数学模型为

(1)

式(1)中：ΔPw为风电有功波动；A为风机有效扫风面积；Vw为风速；ρ为空气的密度；Cp为风功率转换系数；λ为叶尖速比；β为风机桨距角。

当系统遭受风电有功扰动，此时系统的转子运动方程为

ΔPg-ΔPw-ΔPD=DΔω+2HsΔω

(2)

式(2)中：ΔPg为全部发电机机械功率变化量;ΔPD为有功负荷变化量；D为用电负荷的频率调节阻尼常数；Δω为系统发电机转速偏移量；s为拉普拉斯算子；DΔω为有功负荷与频率相关部分变化量;H为系统等效转动惯量；

令Kps=1/D,Tps=2H/fD，其中，f为系统频率，可得发电机与负荷的传递函数GP(s)为

(3)

则对应频率变化可表示为

Δf=GP(s)[ΔPT(s)+ΔPw(s)-ΔPD(s)]

(4)

以西北某地两风电场特征时间段的数据为例，单机为容量1 500 kW的变速恒频双馈风力发电机UP77/1500，其切入风速、切出风速、额定风速分别为3、25、11 m/s，空气密度1.225 kg/m3，风力机直径为77.6 m。截取特征140 s内区域1风电波动工况，根据风机额定功率1 500 kW以及额定风速11 m/s，选取大于70%时段处于额定值±40%以上的波动段，根据图1模型及式(1)～式(4)仿真得到30%风电渗透率下频率偏差如图2所示。

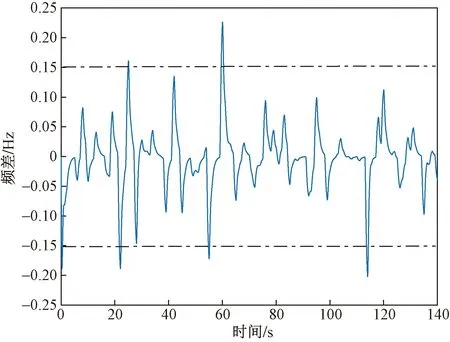
图2 风电渗透率30%下系统频率偏差Fig.2 Frequency deviation of area-1 for 30% wind power penetration

传统的负荷频率控制随着风电渗透率的不断增加，系统的频率偏差不断增大，从图2可以看出，在高风电渗透率达到30%接入下，系统大频差时段已存在超过0.15 Hz时刻，进入了西北电网“两个细则”中的大频差扰动工况，此时新能源场站也需参与一次调频。为避免系统频繁进入大频差扰动工况、保证新型电力系统的安全稳定运行，需要挖掘更充足的可调度资源并提出可调度资源参与下的负荷频率控制方法。

2 需求侧资源主动响应的负荷频率控制模型

需求侧有大量的可调度资源，主要包括：空调、冰箱、热水器、照明负荷和电动汽车等，对其经过集中或分散的控制手段，可以对电压、频率等系统信号做出响应，参与系统调节。其中空调作为一种温控设备具备一定的储能能力，利用房间的保温性能可将电能转换为热能进行短暂储存。人体能够接受的温度舒适范围较大，对于短暂微小的温度变化敏感性较弱，因此空调负荷不仅可以在不影响用户舒适度的前提下快速响应系统调频，而且由于其体量大的优势(夏季高峰期时占尖峰负荷的30%～50%)，具有巨大的调频潜力。

2.1 空调负荷参与的负荷频率控制模型

图3给出了含空调需求侧响应的多区域互联电力系统的LFC模型。

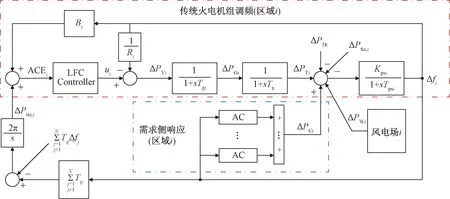
AC为空调需求侧响应模块图3 需求资源参与的多区域电力系统负荷频率控制模型Fig.3 The LFC of the multi-area interconnected power system with demandside response

对于式(4)中的频率响应，加入需求侧响应输出功率后可表示为

Δf=GP(s)[ΔPT(s)+ΔPw(s)+ΔPc(s)-ΔPD(s)]

(5)

式(5)中：ΔPc为空调资源对于负荷扰动的动态补偿功率。

对于空调负荷，常用的模型有定频空调和变频空调两种，定频空调主要是通过控制开断来改变自身功率维持温度的；而变频空调可以通过控制压缩机频率实现用电功率的连续调节，更适合于提供调频服务。选取变频空调模型来研究调频原理，简化空调模型为

Tin(t)=Tin(t-1)+ω[Tout(t)-Tin(t-1)]+μPAC(t)

(6)

式(6)中：Tin(t)、Tout(t)分别为t时刻空调的室内温度和室外温度；ω、μ分别为设备和周围环境特性系数；PAC(t)为t时刻空调的运行功率。

变频空调利用变频器改变压缩机频率控制室温变化，一般以室温Tin与温度设定值Tset的温差ΔT为依据确定压缩机频率。ΔT较大时增加压缩机频率提高排气量，以增加空调制冷能力；接近Tset时则降低压缩机频率。具体变化规律可表示为

(7)

式(7)中：f(t)为空调t时刻的运行频率；fmax和fmin分别为空调运行的最大、最小频率,空调在不停机运行时应满足fmin≤f(t)≤fmax；θmax、θmin分别为温差上下限；K为常系数。

2.2 空调负荷的主动响应模式

空调资源响应调频必然会导致压缩机功率改变，使温度发生变化，进而再通过聚合商对用户空调负荷进行强制改变会造成迟延和出力裕度不足。为了解决这一问题，提出了一种温度自恢复模式。

在频率偏差很小，无需进行频率响应的调频段，设置空调资源响应调频死区fd，设T0为初始设定温度，通过设置一种温度恢复功率，使空调负荷利用死区及时修正室内温度，使之恢复到初始设定。t时刻空调负荷的温度恢复功率计算公式为

PT0(t)={T0-Tin(t-1)-ω[Tout(t)-

Tin(t-1)]}μ-1

(8)

此时在死区的空调输出功率为温度恢复功率PT0，满足设定温度的同时给频率发生大偏差期间的空调出力留出了响应裕度，在需求侧资源需要出力时可以进行功率补偿主动响应。同时结合空调资源自身功率的限制以及用户舒适度的约束，对参与调频响应的变频空调的限值约束为

PAC,min≤PAC≤PAC,max

(9)

式(9)中：PAC为空调入网功率；PAC,max、PAC,min分别为变频空调入网响应的最大，最小输出功率。

由式(7)～式(9)可得空调资源入网主动响应功率为

(10)

式(10)中：fd为调频死区的上界；KAC为频率调节特性系数；Δf(t)为t时刻的频率偏差。

则空调资源对于负荷扰动的动态补偿功率ΔPC可表示为

ΔPC=PAC(t)-PT0(t)

(11)

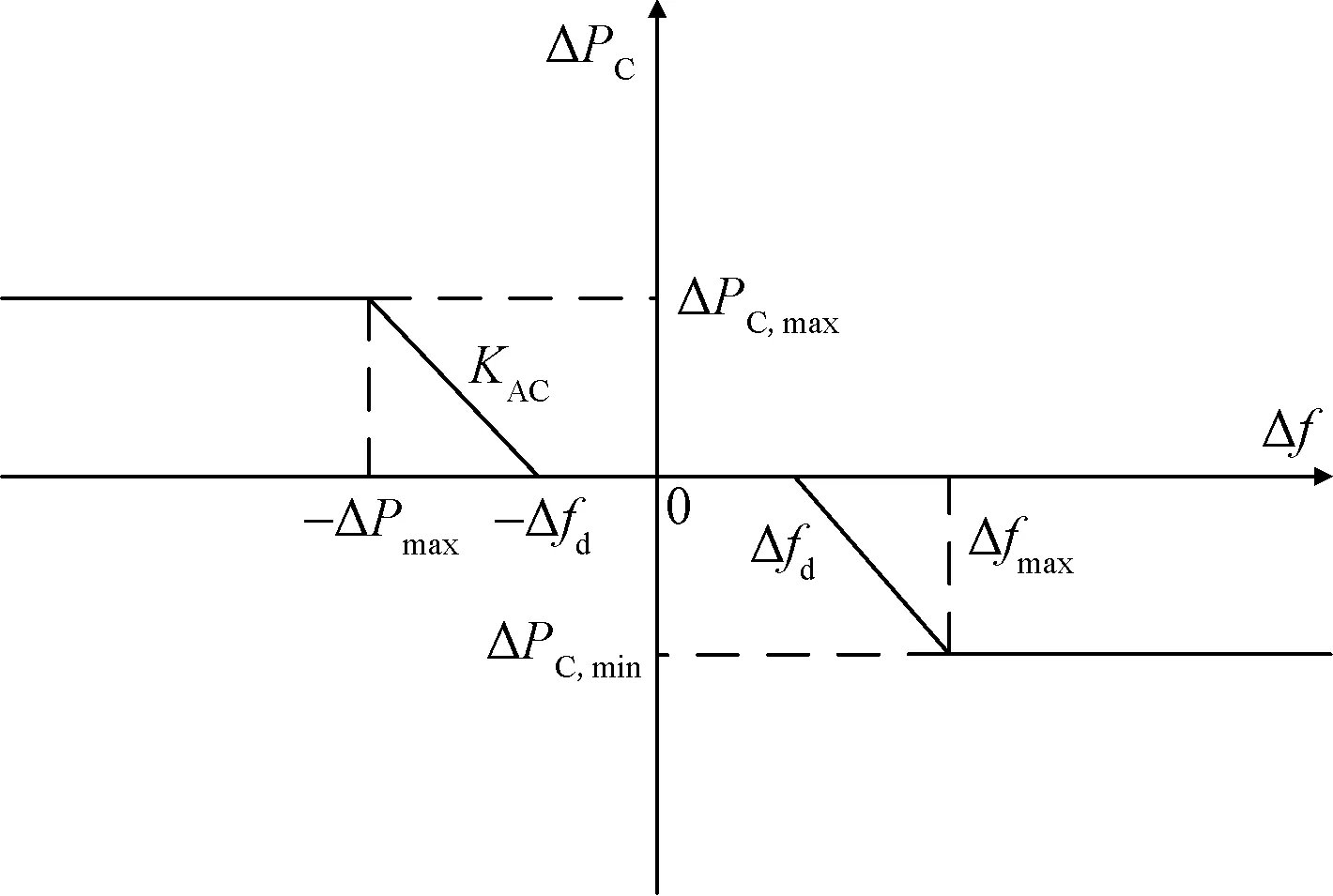
fd和-fd分别为调频死区的上下边界；Δfmax和-Δfmax分别为空调 负荷出力临界点对应的频率限值;ΔPC,max和ΔPC,min分别为参与调频 的变频空调功率响应上下限图4 变频空调频率调节特性Fig.4 Frequency adjustment characteristics of inverter air conditioner

需要说明的是在实际操作中，系统内可参与调频的变频空调总量是实时变化的，图4仅表示某特定时刻变频空调近似的频率调节特性。

3 线性自抗扰控制策略设计

在控制器方面，需求侧资源的主动响应是一种不确定数据，无论大小都将影响到参与调频的机组出力，将相对独立的空调负荷补偿响应视为对调频机组的一种干扰进行分析；而线性自抗扰具有好的抗干扰和振荡抑制性能，而且有独立于模型的普适性控制结构[19]，因此设计自抗扰控制器可以充分激发需求侧资源的主动响应特性。

3.1 多区域线性自抗扰负荷频率控制结构

考虑控制系统可表示为

Y(s)=G(s)U(s)+Gd(s)D(s)

(12)

式(12)中：

(13)

(14)

式中：Y(s)、U(s)和D(s)分别为系统的输出、输入和扰动；G(s)和Gd(s)分别为被控对象和外部扰动的传递函数；b、c为系统开环增益；a为系统闭环特征方程系数，相应下标表示对应阶数复参数s的不同系数。

线性自抗扰控制是将系统看成若干个积分串联型的形式，把其他一切不确定因素和误差看成总干扰将其估计出来，实现无差调节。因此，只需知道负荷频率控制系统的相对阶次p=n-m以及增益b=bm/an就可对频率偏差实现控制，其对象可表示为

y(t)(p)=f[y(t),y(t)2,…,y(t)p-1,u(t),

d(t)]+bu(t)

对于具有以下临床指征的患者采取阴道试产法进行分娩，①患者仅具有一次剖宫产史，且患者的剖宫产位置在患者的子宫下段切口处，患者的自身机体恢复状态良好；②患者的骨产道经过我院医师的检查，结果显示该部位正常，不存在任何不对称的情况[2]；③患者无前次剖宫产指征，且未出现新的剖宫产指征；

(15)

式(15)中：f为系统的总扰动，线性自抗扰控制通过设计线性扩张状态观测器(linear extended state observer, LESO)来估计系统的总扰动f，并通过反馈回路消除扰动对系统的影响。

(16)

式(16)中：

(17)

一个全阶的Luenberger状态观测器可表示为

(18)

(19)

式(19)中：βi为增益向量的各级增益参数值。

根据图3，以两区域互联的电力系统(N=2)为例设计线性自抗扰控制器，具体模型如图5所示。

3.2 参数整定

文献[20]针对多区域电力系统的负荷频率控制提出了一种分散整定方法。该方法先忽略联络线交换功率，分别对单个区域设计线性自抗扰控制器，图5中每个区域机组模型的开环传递函数为

(20)

式(20)中：Tt为汽轮机时间常数；Tg为调速器时间常数；R为调速器调速参数。

由传递函数可以看出，其相对阶次p=3，对于两区域电力系统来说，可分别设计三阶线性自抗扰控制器。

按照文献[21]所述的带宽法，将观测器LESO的带宽与特征值之间联系起来，令I为p+1阶单位矩阵，将观测器极点配置在-ω0处，即

det[|sI-(Ac-L0Cc)|]=sp+1+β1sp+β2sp-1+…+βp+1

=(s+ω0)p+1

(21)

b为控制对象的静态增益；K0为LADRC控制器状态反馈增益；LESO为线性自抗扰的扩张状态观测器；ACE1、ACE2分别为区域1和区域2的区域控制偏差； a12为联络线置换系数；B1、B2分别为区域1和区域2的频率偏差常数；u1、u2分别为区域1和区域2的控制量；R1、R2分别为区域1和 区域2的调速器调速参数，Hz/p.u.；ΔPv1、ΔPv2分别为区域1和区域2调速器输入控制量；Tg1、Tg2分别为区域1和区域2的调速器时间常数； ΔPG1、ΔPG2分别为区域1和区域2的调速器输出指令，p.u.；Tt1、Tt2分别为区域1和区域2的汽轮机时间常数；ΔPT1、ΔPT2分别为区域1和 区域2汽轮机输出功率的变化；ΔPD1、ΔPD2分别为区域1和区域2为负载需求变化扰动；Kps1、Kps2分别为区域1和区域2发电机和负载的增益； Tps1、Tps2分别为区域1和区域2发电机和负载的时间常数；Δf1、Δf2分别为区域1和区域2的频率偏差；AC为空调模块；ΔPC1、ΔPC2分别为 区域1和区域2空调的调频响应功率；T12为区域1连接至区域2的输电线路同步系数；ΔPtie为区域1与区域2之间的联络线交换功率动态偏差图5 需求侧响应参与的两区域电力系统线性自抗扰负荷频率控制模型Fig.5 LADRC of the two-area interconnected power system with demand side response

通过整定ω0的数值就可得到LESO的增益L0。当ω0的值增大时，观测器的速度会加快，同时也会造成LESO对噪声的敏感度提高。对于需求侧资源的主动响应，要选取较高ω0，提高对空调负荷出力的适应度，综合考虑得到最佳数值。

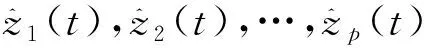
(22)

式(22)中：u0为控制输出量。

将单区域开环阶数p=3 代入式(22)得出图5中每个区域的控制率，可表示为

(23)

将式(21)代入式(13)中，则控制系统可表示为

(24)

y(t)(3)≈u0(t)

(25)

上述对象的控制规律可表示为

(26)

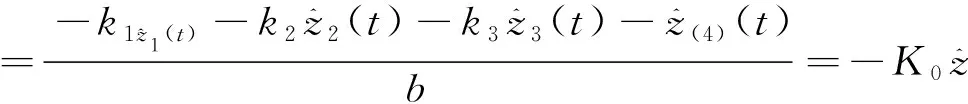
(27)

多区域电力系统设计局部负荷频率控制器时只需要将每个区域的对象都乘以该区域的频率偏差系数[19]，因此，相应的控制量增益可表示为

(28)

同样的，文献[21]将反馈控制器参数通过带宽法全部配置在-ωc处，对于图5中三阶负荷频率控制系统有

s3+k3s2+k2s1+k1=(s+ωc)3

(29)

式(29)中：ωc为自抗扰控制器的控制带宽。

只需调节参数ωc，就可以得到控制器的增益参数K0。改变ωc值，对需求侧资源的响应速度和系统频率的稳定性都有影响，为了充分激发需求侧资源的主动响应特性，需要综合考虑选取最佳的ωc。

4 仿真算例

根据图5设计的两区域互连电力系统，检查所提出的控制策略的性能。每个区域的火电机组额定功率为2 000 MW，额定负载为1 000 MW，根据《西北电网区域发电厂并网运行管理实施细则》，设置调速器死区设为±0.033 Hz，火电机组爬坡约束为机组额定容量的6%。该系统被广泛用于负荷频率控制的设计和分析[22-26]。系统参数的标称值取自文献[1]。区域1和区域2的空调集群数量为2.5×104台，空调集群的初始温度T0为25 ℃，满足正态分布N(25,2)，设空调初始接入时刻的室内温度Tin均已达到设定温度，频差死区Δfd=0.05 Hz，单体最大和最小输出功率限制分别为PAC,max=3 kW，PAC,min=1 kW。图5所示的模型是在MATLAB/Simulink平台上设计的，具体的风电数据和空调负荷频率响应代码由M文件编写并与系统模型连接以实现仿真过程。记文献[20]中整定的PID控制的调频方式为策略1，需求侧响应参与的PID控制为策略2，需求侧响应参与的线性自抗扰控制方法为策略3。其中PID采用的是文献[1]设计的控制器响应参数，三阶线性自抗扰控制器参数根据3.2节和系统参数综合整定得：b=106.25，ω0=100，ωc=3。讨论了以下3种情况的图形和数值模拟结果。

情形1不含风电场的电力系统。在此情形中，假设负载曲线为阶跃扰动，可以通过发电单元的损耗或突然的大负载关断来表示。在t=0 s区域1中将需求的阶跃负载增加10%，对比加入需求侧响应前后,不同控制器的系统频率动态响应，3种控制策略的仿真结果如图6所示。

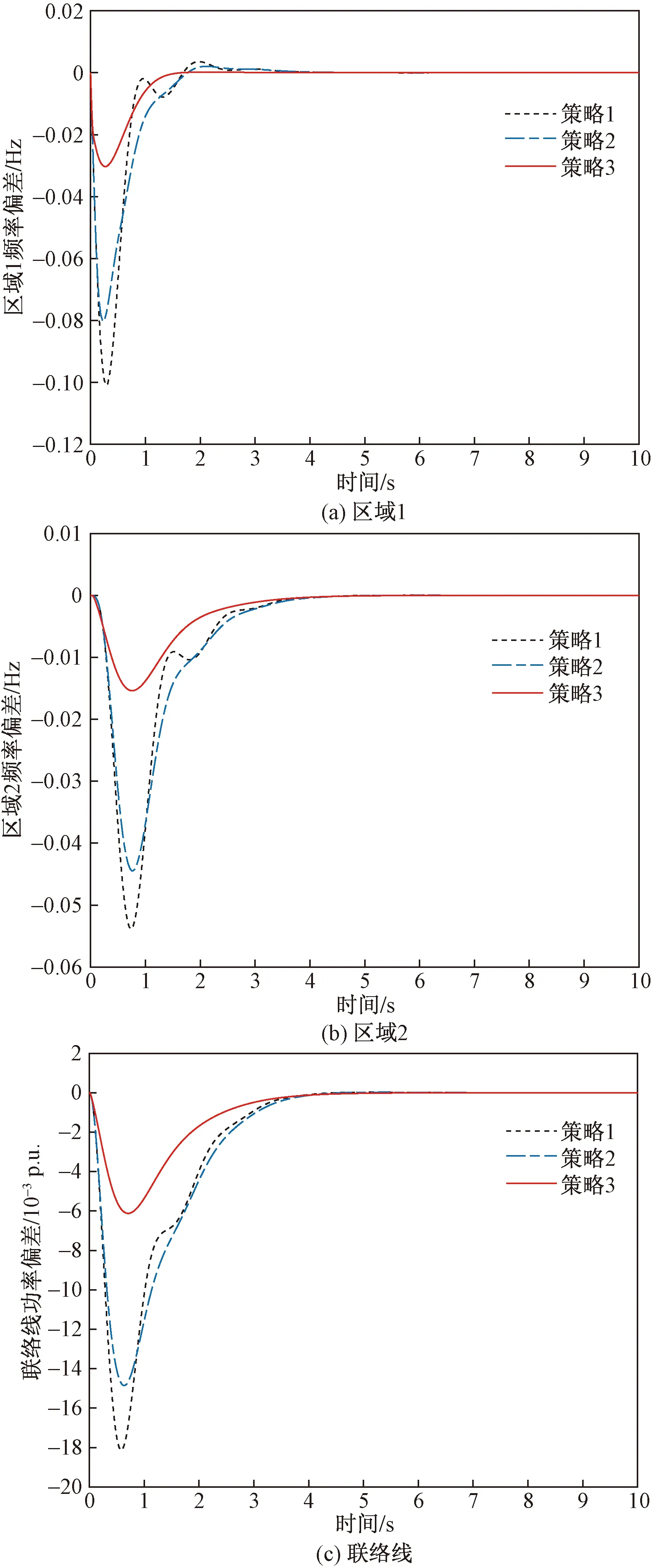
图6 区域1发生10%阶跃负载扰动时的 频率偏差及功率偏差Fig.6 Frequency deviation and power deviation in case of 10% step load disturbance in area-1

从图6可以看出，需求侧响应的加入对减小频率偏差和缩短调节时间具有明显贡献效果。对比文献[20]所设计的两区域PID负荷频率控制策略1，策略2加入需求侧主动响应后，区域1最大频率偏差相比策略1减少了22%，表明需求侧响应参与电力系统调频能够显著降低频率跌落幅度，但采用PID控制可以看出在调节时间方面改善不大。而对比策略2与策略3，在同时应用需求侧主动响应的情况下也可以明显看出，线性自抗扰控制比传统的PID控制器具有更好的动态性能，频率跌落幅度降低了60%，且区域1系统频率和联络线功率偏差分别在1.51 s和3.35 s内快速恢复到零，大大缩短了频率恢复时间。采用仿真输出信号的时间乘误差绝对值积分(integral of time multiplied absolute error，ITAE)性能指标分析如表1所示，其中策略3的ITAE=0.046 8，达到了3个策略中的最小值。可见基于线性自抗扰控制的需求侧资源主动响应与负荷频率控制策略，大大提高了负载扰动下电力系统的频率稳定性，具有更好的控制效果。

表1 10%负载扰动下系统性能比较Table 1 Comparison of system performance for 10% load perturbation

图7 多级负载连续变化Fig.7 Multi load deviation

情形2电力系统多级负载连续变化。为了验证所提的控制策略在LFC实际应用框架的鲁棒性，对电力系统在各种运行条件下进行了一些模拟，包括连续负载变化，作为电网大幅波动以及若干系统参数的变化。图7考虑了在区域1中电力系统多级负载的连续变化。仿真效果如图8所示。可以看出，基于线性自抗扰控制的需求侧资源主动响应与负荷频率控制策略具有的足够能力消除步进增加负载扰动造成的频率偏差，系统频率响应要比传统控制策略平滑得多，频率偏差的过冲和建立时间更小。

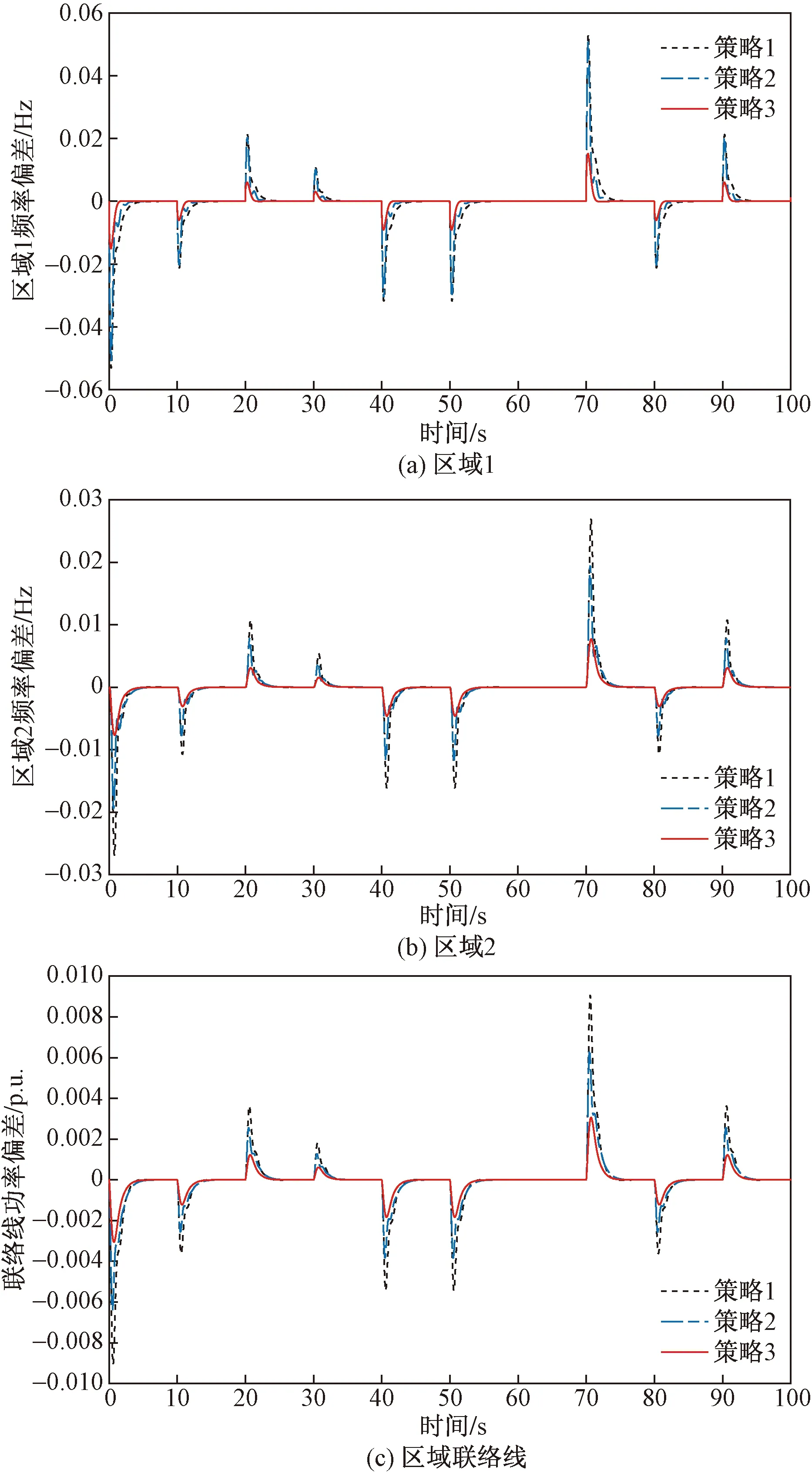
图8 多级负载连续变化下的频率偏差及功率偏差Fig.8 Frequency deviation and power deviation under continuous change of multi-stage load

情形3含风电场的电力系统。对某地两风电场不同层级风电渗透率下的波动情况(图2)应用所提出的基于线性自抗扰控制的需求侧资源主动响应与负荷频率控制策略进行控制效果验证，如图9、图10所示。

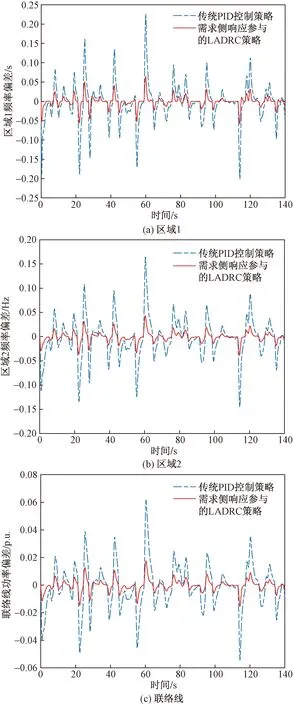
图9 风电渗透率30%下不同控制器偏差Fig.9 Frequency deviation of different controllers for 30% wind power penetration

图10 风电渗透率40%下系统频率偏差Fig.10 Frequency deviation of 40% wind power penetration

从图9、图10可以明显看出，基于线性自抗扰控制的需求侧资源主动响应与负荷频率控制策略使得系统振荡显著减弱。在面对天气条件变化导致大幅度风功率波动时，传统的PID控制策略在30%风电渗透率下已经达到0.15 Hz的频率波动，而所提策略的控制效果基本稳定在0.05 Hz频差内，在低风电渗透率下风电机组可见并没有触发调频动作；根据图10可知，在风电渗透率达到40%的时候，常规风火互联系统中风电以及达到了0.2 Hz的调频动作，而本文所提策略能很好地抑制频率偏差发生大范围变化，在相应的风电渗透率下仍使频差稳定在死区限制的0.1 Hz允许值内。同时在互联区域的风电场发生随机性的风功率波动时，能够使其对本区域的波动影响最小化，并令系统联络线功率有更小的锯齿效应，维持系统频率在较小的范围内波动。

5 结论

先进的调控理论方法和多能源互补的实现对改善电力系统负荷频率控制性能，平抑新能源电力随机波动性十分重要。选取了变频空调负荷这一需求侧灵活可调资源，设计了其主动响应模式，并提出了基于线性自抗扰控制的需求侧资源主动响应与负荷频率控制策略。通过对含风电的某两区域互联电力系统进行仿真验证，结果表明所提方法可以显著改善系统的负荷频率控制性能，得出如下结论。

(1)在10%负载扰动下，所提策略能够将频率跌落幅度减少50%，原区域频率恢复时间显著缩短至3 s级，并且有效地控制了联络线功率的波动，ITAE指标达到了最优的0.046 8。

(2)对于多级负载的连续变化，所提策略具有的足够能力消除步进负载扰动造成的频率偏差，系统频率响应要比传统控制策略平滑得多，具有较强的鲁棒性。

(3)在30%高风电渗透下，计及需求侧主动响应的线性自抗扰控制能很好地抑制频率偏差发生大范围变化，使频差稳定在0.15 Hz的风电调频动作死区内，同时使系统联络线功率波动影响最小化，显著提升了含风电互联系统的负荷频率控制品质，对于规模化新能源接入电网具有很好的支撑作用。