基于参数优化神经网络的海底油气管道腐蚀泄漏预测

鲁中歧， 肖文生， 崔俊国*， 张杨， 王魁涛， 尹丰

(1.中国石油大学(华东)机电工程学院， 青岛 266580；2.中海油研究总院有限责任公司， 北京 100028)

油气资源开采逐渐向深海转移，海底油气管道担任起油气运输的重任，但在运作过程中不可避免地会出现因腐蚀等原因导致的泄漏失效，污染自然环境，甚至危害工作人员生命安全，因此一种海底管道腐蚀泄漏预测技术的开发极有必要。该预测技术的研发，在海洋油气运输安全方面具有重要意义。

目前中外学者在该领域已展开深入研究，提出了灰色预测模型，灰色理论与马尔可夫链结合的预测模型以及一些机器学习算法，如随机森林、神经网络等也逐渐应用于海底管道腐蚀泄漏的预测中。Valor等[1]提出了两种利用马尔可夫链建立的不同的点蚀模型，对点蚀坑的生长进行了预测； Ren等[2]将反向传播(back propagation，BP)神经网络应用于长输管道腐蚀速率的预测，建立管道内腐蚀速率预测模型，预测结果较为可靠。还有许多学者将多种算法综合运用，提出了组合预测模型。骆正山等[3]提出了一种利用随机森林(random forest，RF)筛选腐蚀因素相关变量，蝗虫算法(grasshopper optimization algorithm，GOA)优化相关向量机(relevant vector machine，RVM)的预测模型，稳定度和准确度相比于传统单一模型得到了提高；骆正山等[4]还采取主成分分析法(principal component analysis，PCA)对试验所得数据进行降维，用天牛须搜索(beetle antennae search，BAS)算法优化投影寻踪回归(projection pursuit regression，PPR)预测模型对海底管道腐蚀速率展开预测，为管道腐蚀预测提供了新思路；张新生等[5]在对腐蚀数据进行因子分析降维处理以后，建立了改进的随机森林模型对海底管道腐蚀速率进行预测，该模型稳定性较好。

目前，一些模型的单一应用或多或少的会出现误差较大、欠学习、过拟合等问题，而组合模型存在未考虑变量之间相互影响关系、过多考虑预测精度导致计算量增加、专注于模型稳定性导致预测精度下降等问题。基于以上问题，采用斯皮尔曼相关系数寻找各自变量因素中相关性较高的因素，采用随机森林(random forest，RF 重要性评估的方法在各腐蚀影响因素对腐蚀速率的贡献度方面进行排序，并剔除相关性较高的因素中对腐蚀速率贡献度较低的变量因素，选用筛选后的影响因素建立粒子群(particle swarm optimization，PSO)算法优化的前馈神经网络(back propagation neural network，BPNN)预测模型进行腐蚀速率的预测。以期为海底管道泄漏风险的精准预测以及高效控制提供依据。

1 研究方法

1.1 斯皮尔曼相关系数

斯皮尔曼相关系数可以用来衡量两个变量之间的相关性，取值范围为[-1,1]，计算公式为

(1)

式(1)中：rs为斯皮尔曼相关系数；n为样本数；di为排序(升序或降序)好后的两个变量之间的等级差。

当一个变量表现为增加趋势时，另一个变量同样趋向于增加，则相关系数为正，反之为负，相关系数的绝对值越接近于1，相关性越强，越接近于0，相关性越弱。

1.2 随机森林重要度评估

通常情况下，一个数据集往往有多个特征，如何选择对结果影响较大的那几个特征，以此来缩减建立模型时的特征数是一个问题，选用随机森林重要性评估的方法对影响腐蚀速率的多个因素进行重要度排序。

随机森林在选取数据集训练决策树时，采用对输入样本集合进行多次放回重复抽样[6]的方法，该方法会导致样本集合中有数据多次重复出现，同时也说明在一个样本集合中，会有部分数据不参与决策树训练，该部分数据称之为袋外数据，在特征变量选择中，就是基于袋外数据对每个特征变量重要性进行计算，然后排序，选择重要性较高的特征为后续模型的建立做准备。其中，对于某个特征的重要性计算步骤如下[7]。

Step1选择每一棵决策树相应的袋外数据进行袋外数据误差计算，记为Error1i。

Step2随机加入干扰信号，重复步骤1，记为Error2i。

Step3假设森林中有N棵树，则该特征的重要性I可表示为

(2)

若干扰信号加入后，袋外数据准确率下降幅度较大，说明该特征重要程度较高。

1.3 粒子群算法

PSO属于进化算法的一种，其算法规则较为简单，具有实现容易、收敛快、精度高等优点[8]。该算法中粒子根据种群最优和个体最优两个因素来实现自我更新，在找到这两个最优值后，粒子通过以下公式实现自己速度和位置的更新[9-11]。

速度更新公式为

vi=ωvi+c1rand(·)(pbesti-xi)+

c2rand(·)(gbesti-xi)

(3)

式(3)中：vi为粒子速度；i=1,2，…，N′，其中N′为粒子总数；ω为惯性因子；c1、c2为学习因子，通常取2；rand(·)为[1 2]的随机数；pbesti为个体最优；gbesti为种群最优；xi为当前粒子所在位置。

位置更新公式为

xi=xi+vi

(4)

1.4 BP神经网络

输入、输出层及隐层构成神经网络的网络拓扑结构，各层之间有相应连接权值[11-12]， BP神经网络的主要思想是：输入学习样本，经反复训练，使输出值与期望值尽可能地接近，当误差低于指定要求后，将网络权值和偏差进行保存，完成训练[13]。具体步骤如图1所示。

W、b分别为各层之间的权值、阈值矩阵图1 神经网络模型建立流程图Fig.1 Flow chart of neural network model establishment

图2 预测模型建立流程图Fig.2 Flow chart of prediction model establishment

2 模型构建

2.1 模型建立

对海底管道腐蚀速率的影响因素进行斯皮尔曼相关性分析，随后采用随机森林袋外数据误差进行影响因素重要性排序，筛选重要性高的特征参与粒子群优化-反向传播神经网络(particle swarm optimization-back propagation neural network，PSO-BPNN)预测模型的建立，完整模型的建立流程图如图2所示。

基于RF-PSO-BPNN海底管道腐蚀预测模型，经数据筛选后，避免了大量强相关性数据影响建模的冗余度及精确度问题，数据维度的降低有助于提高模型优化及训练的速度，具体运行过程如下。

Step1数据预处理。计算初始样本各影响因素之间斯皮尔曼相关系数，分析其相关性，找出相关性较大的特征；将初始样本数据进行标准化处理，利用随机森林袋外数据误差进行各影响因素的重要性排序，剔除上述相关性较大的因素中重要性较小者，并按照重要性排序选取重要性较大的特征进行后续建模。

Step2模型参数的确定。设定粒子群种群规模、进化次数、权重因子等参数，完成粒子位置、速度的初始化；确定神经网络拓扑结构、训练次数、学习速率及训练目标等参数。

Step3模型训练。将筛选后的数据进行归一化处理后，分为训练集和测试集，训练集用于模型的训练，测试集用于模型的检验。

Step4模型检验。根据测试集预测结果，计算均方误差、平均绝对误差等来对所建立的模型进行评价。

2.2 模型检验

为验证RF-PSO-BPNN海底管道腐蚀预测模型的预测精度，采用平均绝对误差(mean absolute error，MAE)、均方误差(mean square error，MSE)以及决定系数R2来对模型进行检验评价，计算公式为

(5)

(6)

(7)

3 实例分析

3.1 数据预处理

以某海底管段为例，进行实海腐蚀挂片实验，部分腐蚀实验数据如表1[4]所示。

用式(1)计算n1～n7影响因素中两两之间的斯皮尔曼相关系数，相关系数矩阵如图3所示。

由图3可知，部分影响因素之间存在较强的相关性，而强相关性的因素不仅会增加模型的冗余度还会影响模型精度，因此分析相关性后需进行降维处理，图中斯皮尔曼相关系数超过0.55的有pH(n5)和氧化还原电位(n4)、pH(n5)和附着海洋生物(n6)、温度(n1)和附着海洋生物(n6)。接下来采用随机森林计算各影响因素对腐蚀速率的重要度。首先用式(8)将表1中的腐蚀数据进行标准化处理。

(8)

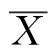
确定随机森林参数叶子大小及决策树的数量，分别取叶子大小为5、10、20、50、100，决策树数量为200，将训练数据按照式(8)进行标准化处理，以消除不同因素量纲不同对模型精度的影响，代入标准化后的数据进行训练，训练结果如图4所示。

由图4可知，红色线始终处于最低位，即在上述5种叶子大小中，当叶子大小为5时均方误差最小，各曲线在树的数量到达50时便不再有大幅度的下降，故在该模型中，叶子大小选取5，决策树的数量选取50较为合适。选取以上参数建立随机森林模型，进行各影响因素重要度计算并排序，如图5所示。

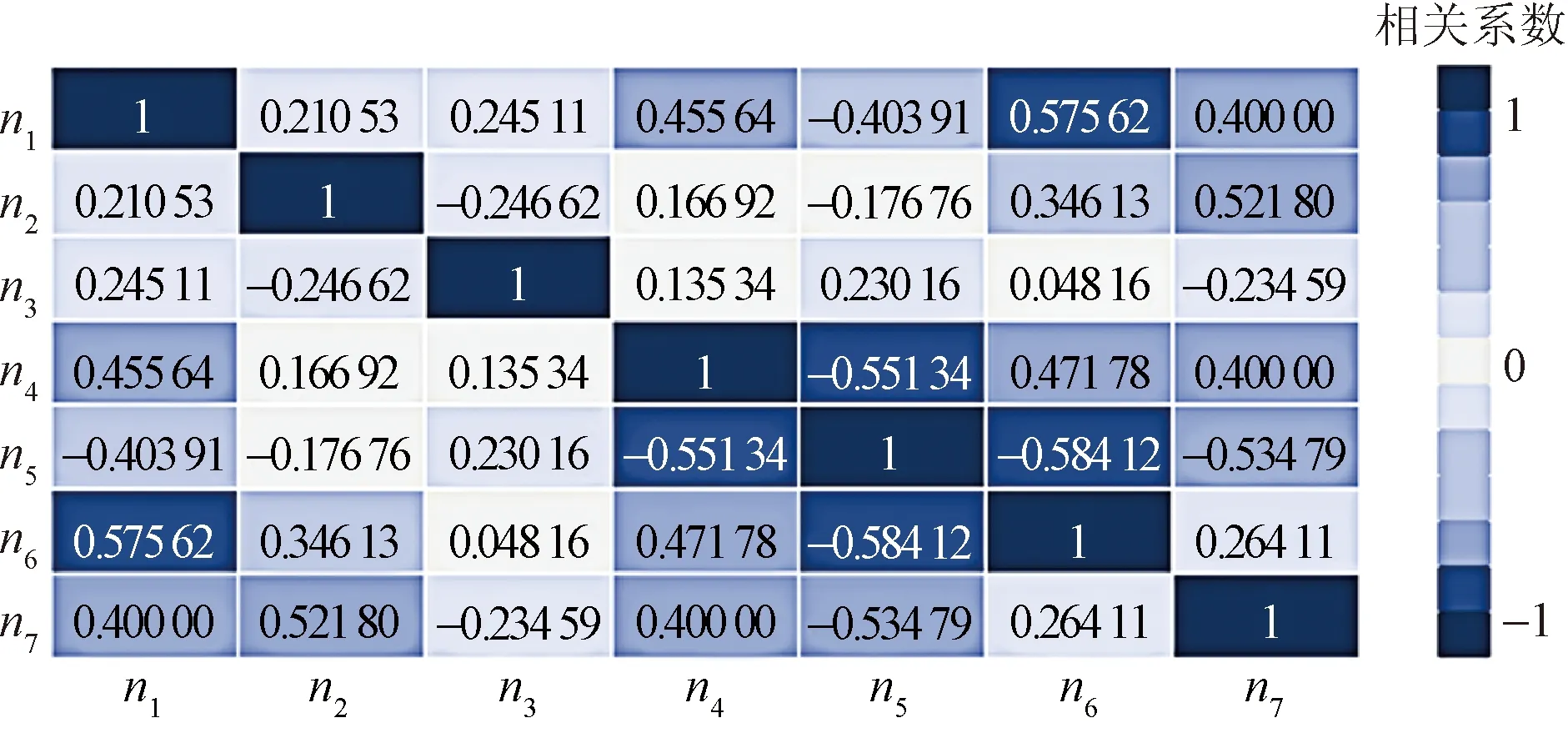
图3 斯皮尔曼相关系数矩阵Fig.3 Spearman correlation coefficient matrix

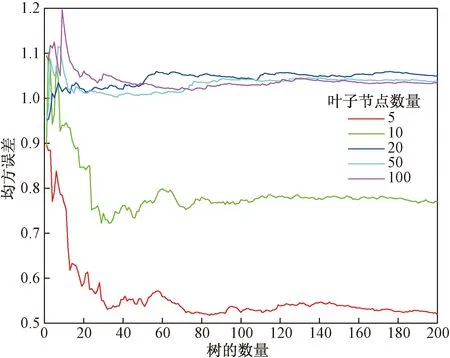
图4 RF模型参数择优Fig.4 RF model parameter optimization

表1 部分腐蚀试验数据Table 1 Partial corrosion test data

图5 变量重要性排序Fig.5 Importance ranking of variables

由图5可知，变量重要性依次为：pH(n5)、附着海洋生物(n6)、溶氧量(n2)、含盐度(n3)、温度(n1)、海水流速(n7)、氧化还原电位(n4)。结合上述斯皮尔曼相关性分析，pH(n5)和氧化还原电位(n4)、附着海洋生物(n6)相关性较强，而pH重要性较高，故剔除氧化还原电位和附着海洋生物两项影响因素，剔除后按照重要性排序选取前4项影响因素分别为：pH(n5)、溶氧量(n2)、含盐度(n3)、温度(n1)。

3.2 模型参数确定

3.2.1 RFR模型参数确定

根据图5及3.1节的分析，选取叶子大小为5，决策树数量为50建立随机森林回归模型，当样本数量足够大时，由于随机森林采用放回抽样加交叉验证，所以一般不会出现过拟合的现象，而样本数量较少时，不划分训练集、测试集大概率会出现过拟合现象，因此在此选用总样本的75%作为训练集，剩下的25%作为测试集进行随机森林回归模型的建立。

3.2.2 BPNN模型参数确定

将筛选后的数据进行归一化处理，神经网络数据集的划分，若训练集划分过少容易出现训练力度不足的问题，若训练集过多，测试集过少则无法确定所训练模型的好坏。根据现有数据规模，选取总样本集的75%作为训练集，25%作为测试集。依据上述筛选出的数据，将4个影响因素作为输入，腐蚀速率作为输出。故BP神经网络中输入层神经元个数为4，输出层神经元个数为1，隐层神经元个数的确定至关重要，根据经验公式[式(9)]确定为10，最大迭代次数为300次，期望误差为0.000 1，学习速率设置为0.01，激活函数选择Sigmoid函数，计算公式为

(9)

式(9)中：l为隐层神经元个数；m为输入层神经元个数；nneu为输出层神经元个数；a为隐层神经元个数计算经验公式的辅助计算参数，取值为1～10。

(10)

所建立的神经网络结构拓扑图如图6所示。

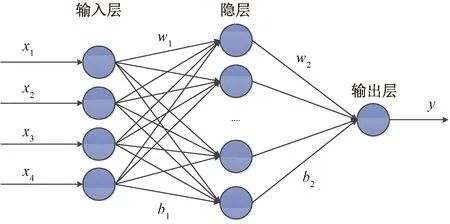
x1～x4为输入变量；y为输出变量； W1、W2分别为输入层到隐层、隐层到输出层的权值矩阵； b1、b2分别为输入层到隐层、隐层到输出层的阈值矩阵图6 神经网络拓扑结构图Fig.6 Topology of neural network

3.2.3 PSO参数确定

按照文献[14]，c1、c2取2，种群规模为30，迭代次数为150，为避免陷入局部最优或全局最优，设置动态权重因子w，其表达式为

(11)

式(11)中：we、ws为粒子群优化算法中动态权重因子的调节系数，ws取0.9，we取0.1；i为当前迭代次数；mtotal为总迭代次数。

3.3 结果分析

按照3.2节参数设置，带入筛选后的数据分别进行5次模型训练，MAE、MSE和R2分别按照式(5)～式(7)来进行计算，并计算5次训练结果的平均值，其中BP神经网络预测模型各评判标准如表2所示，预测结果与实际值曲线如图7所示。

测试集预测结果曲线如图8所示，随机森林回归预测模型5次训练的各评判标准如表3所示。

由表2、表3可知，随机森林回归预测模型MAE和MSE的5次训练结果平均值分别为1.289 96、2.804 12，均低于BP神经网络模型的1.593 46和3.370 44，可见该模型误差较小，但决定系数为0.620 62，较神经网络模型低0.13，即预测值与实际值的相关性较弱，拟合度较差，在进行长期预测时，难免会出现较大误差，反观BP神经网络预测模型，由图7、图8可知，预测值与实际值趋势较为一致，因此只需优化算法进行优化，提高预测精度即可，采用粒子群优化算法来优化神经网络的权值和阈值，建立了PSO-BPNN预测模型，预测结果如下。

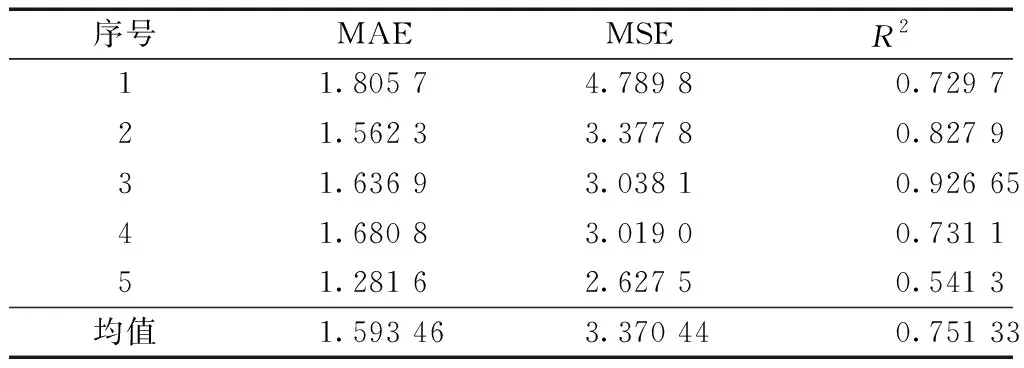
表2 BP神经网络模型预测结果分析Table 2 Analysis of prediction results of BP neural network model

图7 神经网络测试集预测结果曲线Fig.7 Curves of prediction results of neural network test set

图8 随机森林回归模型测试集预测结果曲线Fig.8 Curves of prediction results of test set of random forest regression model

根据3.2节设置好的参数进行粒子群算法的迭代过程，如图9所示。其中以神经网络预测值误差作为适应度值，由图9可知，在迭代次数进行到约20次时，已达最优，将优化好的权值、阈值重新赋予BP神经网络预测模型，再次进行训练建模，模型评判指标如表4所示，预测值与真实值曲线如图10所示。

表3 随机森林回归模型预测结果分析Table 3 Analysis of prediction results of random forest regression model

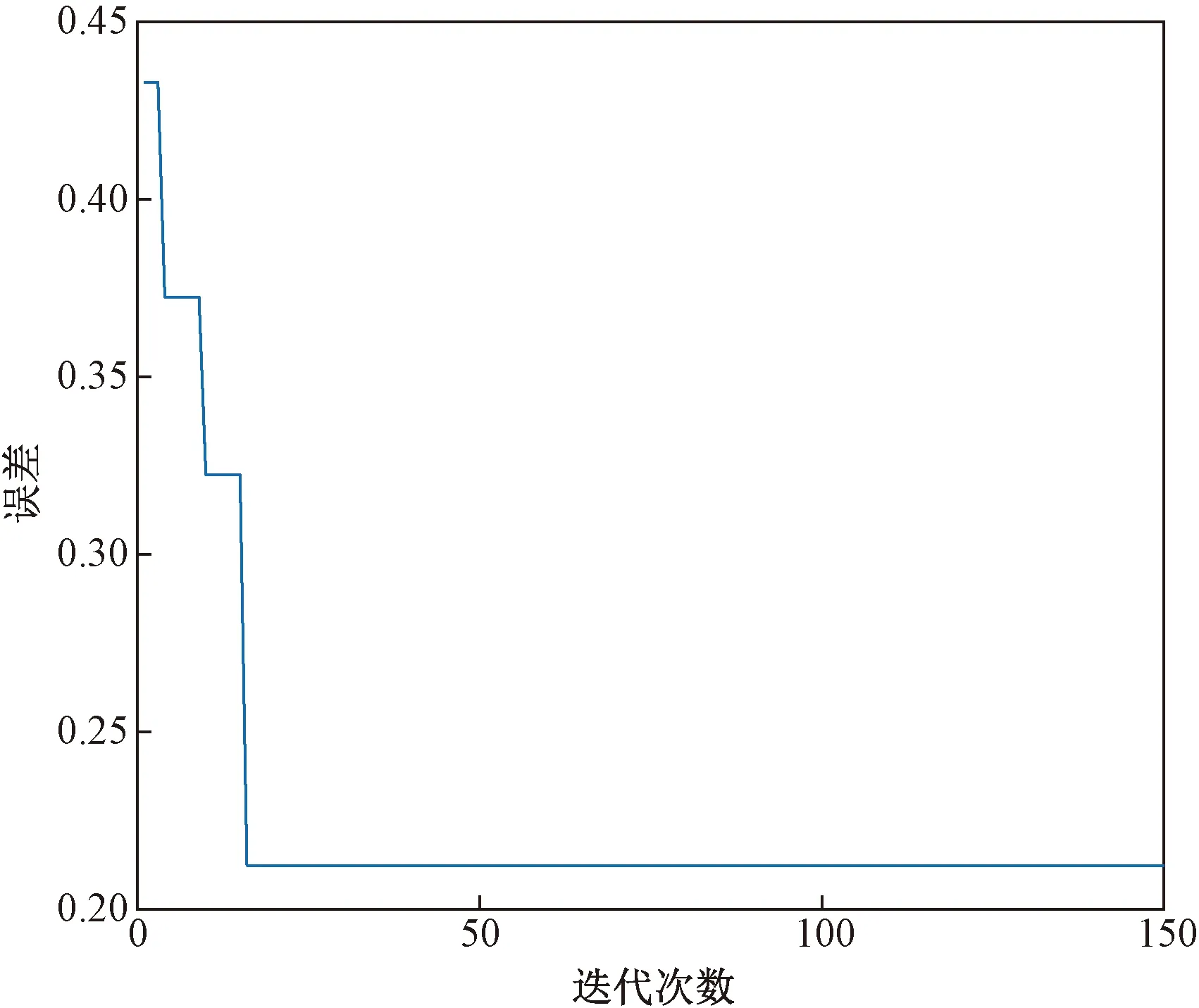
图9 粒子群算法迭代过程Fig.9 Iterative process of particle swarm optimization algorithm

表4 PSO-BPNN模型预测结果分析Table 4 Analysis of prediction results of PSO-BPNN model

由表4可知，经优化后的BP神经网络预测模型MAE、MSE分别为0.790 09、0.729 37，比未优化的神经网络预测模型提高了0.803 37、2.641 07，预测精度有了显著提升，R2为0.915 1，接近于“1”，相比于随机森林和未优化的BP神经网络两种模型也都有了显著的提高，证明了PSO-BPNN海底管道腐蚀预测模型预测性能更优，可为海底管道腐蚀泄漏预测研究提供参考。

4 软件编制

基于以上所建立模型，编制了一款集神经网络、随机森林以及粒子群优化下的神经网络为一体的多模型管道腐蚀预测软件，该软件包括随机森林回归预测、神经网络预测和粒子群优化下的神经网络预测3个模块，操作过程如下。

图11为登录界面，用户输入相应账号及密码即可进入软件。

首先进入软件主界面，如图12所示，用户根据自己需要选择合适的模型，点击左侧栏相应模型下的确认按钮即可进入该模型进行预测。

软件各预测模块截面如图13所示，将经验数据读取后，输入各模型相应参数，即可完成模型的训练，在右侧栏及模型检验处可查看该次训练模型的优劣，模型训练完成后，读取所要预测数据，点击预测按钮即可实现该读入数据的预测。

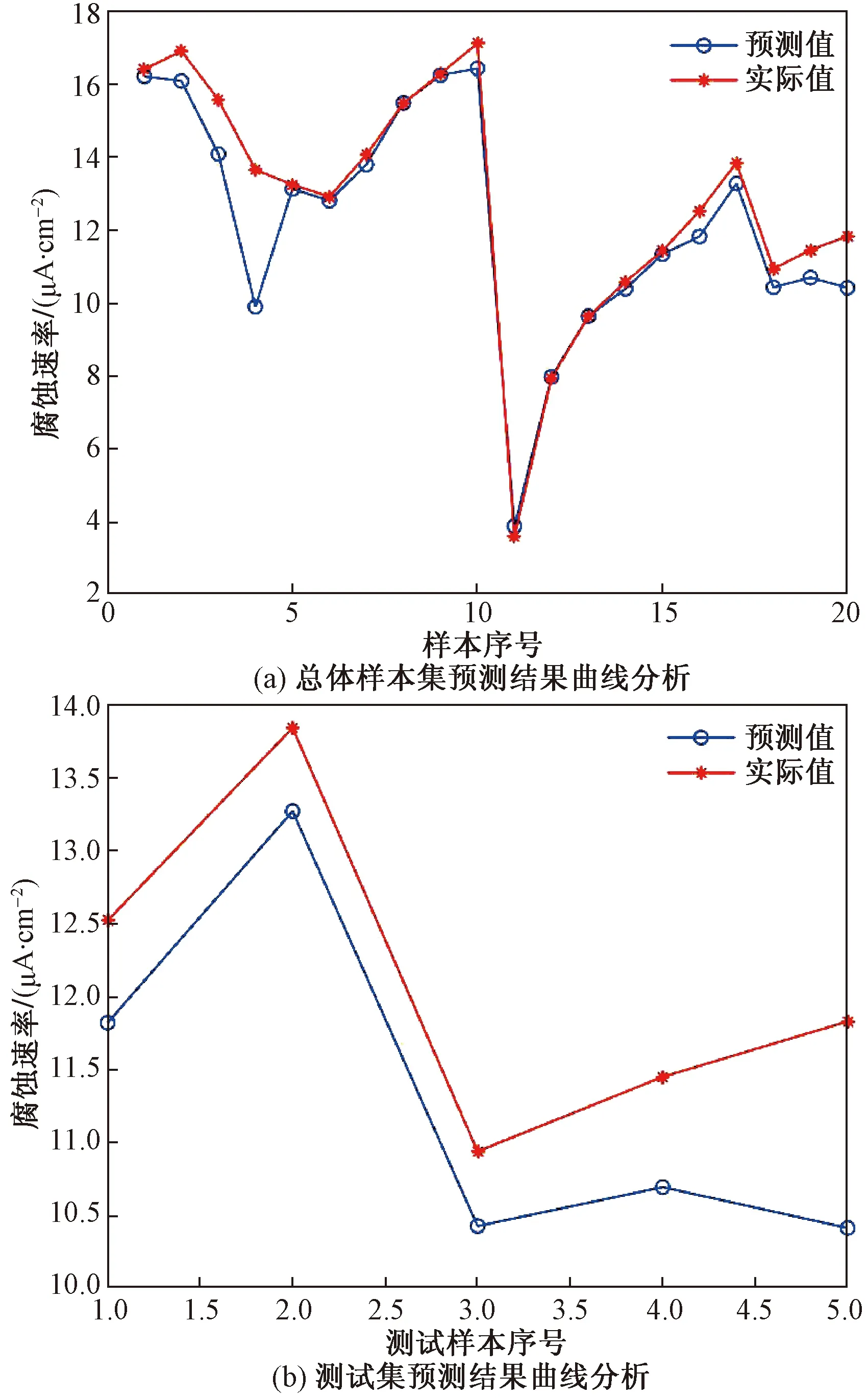
图10 PSO-BPNN预测模型预测结果分析Fig.10 Analysis of prediction results of PSO-BPNN prediction model

图11 登录界面Fig.11 Login interface

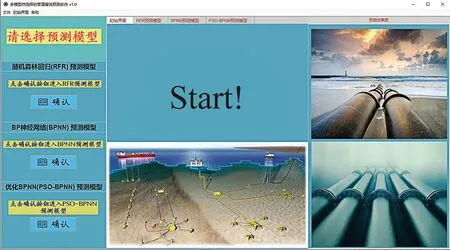
图12 软件主界面Fig.12 Software main interface

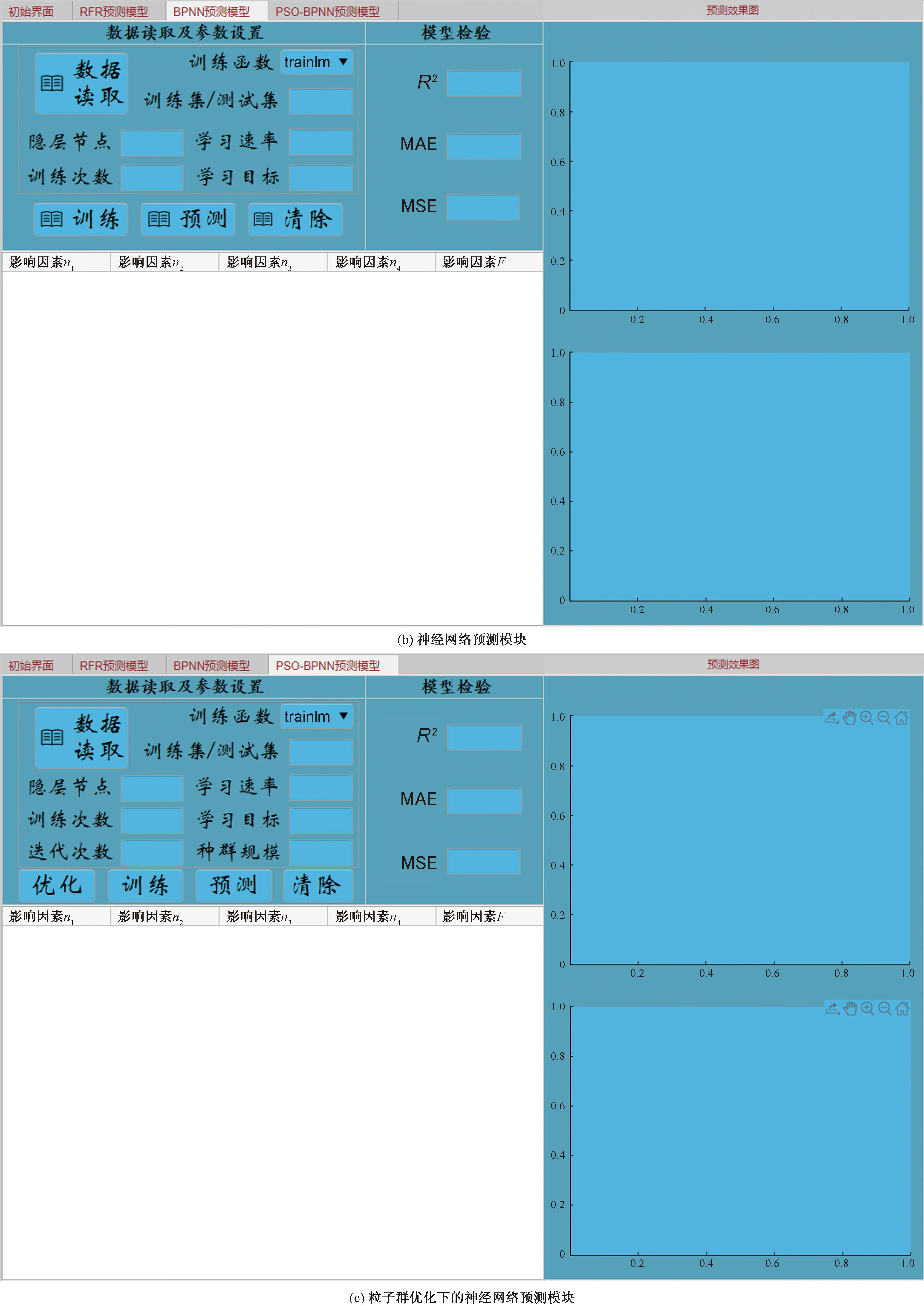
图13 软件预测界面Fig.13 Software prediction interface

该软件与所述模型相对应，用户可根据不同需求选择不同的预测模型来实现相应的功能，模型的训练不需反复的去调整程序，只需简单的修改界面参数即可完成，方便快捷，上手简单，易于操作，极大节省了不同条件下的数据预测时模型的建立时间。

5 结论

针对现有管道腐蚀预测模型的局限性，提出了一种基于RF-PSO-BPNN的海底管道腐蚀泄漏预测模型，并验证了其可行性，得出如下结论。

(1)影响海底管道腐蚀速率的因素有许多，且一些影响因素间存在较强相关性，在此先采用斯皮尔曼相关系数对影响因素间的相关性进行分析，找出相关性较强的因素，随后采用随机森林进行影响因素重要性排序，剔除掉相关性较强且重要性较小的因素，成功筛选出重要性较高且相关性较弱的四项因素，有效降低了因素间相关性及因素的冗余性对预测精度的影响。

(2)对比BPNN和RFR两种预测模型，发现BPNN预测模型较RFR拟合度较好，但预测精度稍差，因此采用PSO优化算法对BPNN的权值、阈值进行优化，建立了PSO-BPNN预测模型，该模型MAE仅为0.790 09，比未优化的模型提高了0.803 77，MSE提高了2.641 07，且R2为0.915 14，接近于1，可见优化后的模型在预测精度及拟合度等方面都有了显著的提高。可对不同工况下的油气运输管道腐蚀泄漏风险进行较为精准的预测，延长海底油气管道的生命周期。

(3)基于所建立模型，编制了管道腐蚀预测软件，使管道腐蚀泄漏预测工作更为简单方便。