工业机器人PTP运动的研究与仿真
郑博涛,郭永胜,潘冠东
(辽宁加宝石化设备有限公司,辽宁 营口 115004)
0 引言
压力容器生产制造企业在采购材料后,需要按照批号、材质和标准等摆放,考虑人工劳动强度及摆放效率,应用机器人代替人工进行作业,将人们从繁重的生产任务中解放出来。为了使工业机器人能够较为理想地完成人们预定的要求,则需要对工业机器人的运动进行研究。PTP运动(即点到点的运动)是工业机器人的主要运动方式之一,工件搬运工作都是通过点到点的运动来完成的,工业机器人的使用大大提高了工作效率,降低了企业的生产成本[1]。因此,本文通过对工业机器人的建模来对工业机器人PTP运动进行仿真分析,进而确保机器人在工作过程中的使用性能[2]。
1 机器人参数及连杆坐标系的建立
本文以FANUC R-2000iB型工业机器人为研究对象(见图1),其所有关节均为转动关节,前三个关节控制机器人末端在空间中的位置,后三个关节控制机器人末端的方向。为了研究机器人末端位姿在基础坐标系中的表示,在每个连杆上固接了一个坐标系,由D-H法则确定相邻连杆之间的位姿,通过坐标变换即可得出机器人末端在基础坐标系中的位姿,建立好的机器人连杆坐标系如图2所示。
2 运动学分析
运动学是规划操作臂轨迹的基础,主要研究机器人关节变量与机器人末端在空间中的位姿对应关系,通过确定机器人连杆参数就可建立其运动学方程。确定连杆参数的方法如下:
(1) 关节转角θi是由xi-1坐标轴到xi坐标轴绕着zi坐标轴所测得的角度。
(2) 连杆扭角αi-1是由zi-1坐标轴到zi坐标轴绕着xi-1坐标轴测得的角度。
(3) 连杆长度ai-1是zi-1坐标轴到zi坐标轴沿xi-1坐标轴所测得的距离。
(4) 连杆偏距di是xi-1坐标轴到xi坐标轴沿zi坐标轴所测得的距离。

图1 FANUC R-2000iB工业机器人
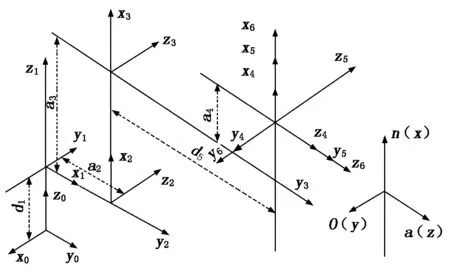
图2 机器人连杆坐标系
由上述定义及图2建立的坐标系可得R-2000iB型工业机器人的连杆参数,如表1所示。
由D-H法则可得相邻两个连杆的位姿关系,通过齐次矩阵变换得到机器人末端在基础坐标系中的方位描述06T,具体如下:
06T==nxoxaxpxnyoyaypynzozazpz0001.
其中:分量nx、ox、ax为机器人末端相对于坐标系{O}的x轴的角度向量;分量ny、oy、ay为机器人末端相对于坐标系{O}的y轴的角度向量; 分量nz、oz、az为机器人末端相对于坐标系{O}的z轴的角度向量;px、py、pz为机器人末端相对于坐标系{O}的位置坐标。
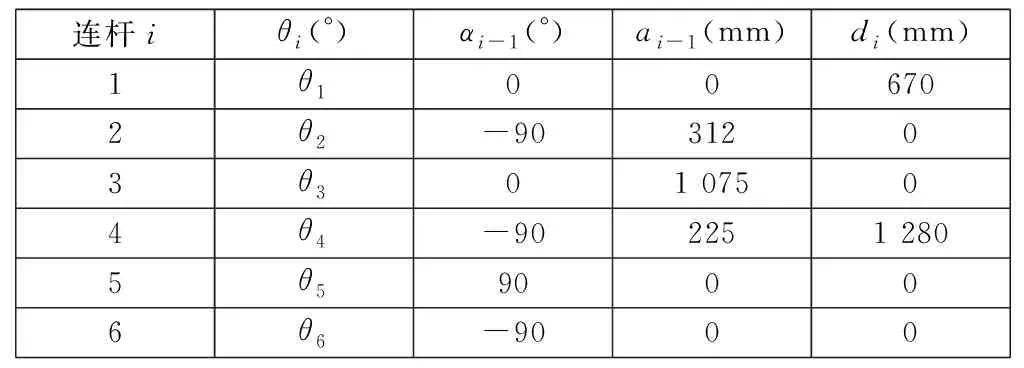
表1 机器人连杆参数
3 运动学仿真
本文使用MATLAB软件中的机器人工具箱进行运动学仿真,通过调用内部的函数而不需要复杂的编程即可实现运动学仿真,很大程度上简化了编程人员的工作任务,提高了对机器人运动学的研究效率[3-5]。
通过调用Link函数、Robot函数与drivebot函数即可建立工业机器人的三维模型(见图3),调用格式为L=LINK([alpha A theta D sigma],‘standard’)。其中,前4个参数分别表示连杆扭角、杆长、关节转角、偏距;sigma代表关节是旋转还是移动关节,0是旋转关节,1是移动关节;standard表示使用标准的D-H参数进行建模。Robot函数将所有的连杆结合成一个整体,调用drivebot函数可以弹出关节滑块控制器(见图4)。具体的建模如下:
L1=link([0 0 0 670 0],’standard’);
L2=link([-pi/2 312 pi/2 0 0],’standard’);
L3=link([0 1075 pi 0 0],’standard’);
L4=link([-pi/2 225 pi 1280 0],’standard’);
L5=link([pi/2 0 pi 0 0],’standard’);
L6=link([-pi/2 0 0 0 0],’standard’);
r=robot({L1 L2 L3 L4 L5 L6});
r.name=’R-2000iB’;
drivebot(r);
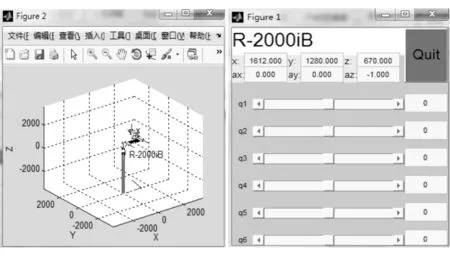
图3 机器人三维模型 图4 机器人关节滑块控制器
这里随机选取了两组关节变量,以机器人末端在空间中的位置为研究对象,通过对比计算得到的位置与仿真得到的位置来确定06T建立的正确与否。两组变量值分别为q1=[0.188 5 0.439 82 -0.125 66 0.251 33 0.314 16 -0.251 33],q2=[0.439 82 0.376 99 0.188 5 0.062 832 0.251 33 -0.314 16]。所得数据如表2所示。
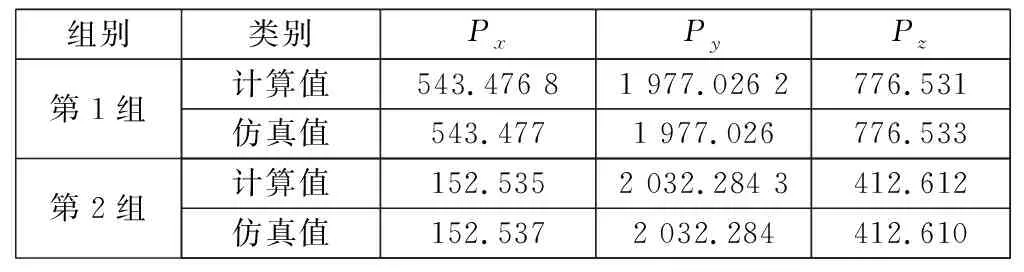
表2 机器人末端位置计算值与仿真值比较
分析比较上述数据,可以发现通过计算得到的位置数据与仿真得到的位置数据误差较小,这说明上述建立的机器人末端在基础坐标系下的位姿矩阵06T是可靠的。
4 PTP运动仿真
PTP运动只考虑初始点与终止点的位置,不需考虑机器人末端在三维空间中走过的具体运动轨迹,这样只需在关节空间进行轨迹规划即可,大大减少了计算量并避免了工业机器人发生奇异的情况。所谓轨迹规划就是规划关节角位移、关节角速度、关节角加速度随时间变化的情况。同时,轨迹仿真也可以帮助人们更直观地理解PTP运动的过程[6-8]。设定初始关节变量q1=[0 0 0 0 0 0],q2=[pi/4 pi/3 pi/5 pi/4 pi/2 pi],运动时间设定为2 s,通过如下的仿真程序,可以较为清晰地观看到机器人从变量q1运动到q2的过程。
L1=link([0 0 0 670 0],’standard’);
L2=link([-pi/2 312 pi/2 0 0],’standard’);
L3=link([0 1075 pi 0 0],’standard’);
L4=link([-pi/2 225 pi 1280 0],’standard’);
L5=link([pi/2 0 pi 0 0],’standard’);
L6=link([-pi/2 0 0 0 0],’standard’);
r=robot({L1 L2 L3 L4 L5 L6});
r.name=’R-2000iB’;
qz=[0 0 0 0 0 0];
qr=[pi/4 pi/3 pi/5 pi/4 pi/2 pi];
t=0:0.1:2;
q=jtraj(qz,qr,t);
[q,qd,qdd]=jtraj(qz,qr,t);
subplot(3,3,1);plot(t,q(:,1));grid;xlabel(’t/s’); ylabel(’rad’); title(’关节1位移变化曲线’);
subplot(3,3,2);plot(t,q(:,2));grid;xlabel(’t/s’); ylabel(’rad’); title(’关节2位移变化曲线’);
subplot(3,3,3);plot(t,q(:,3));grid;xlabel(’t/s’); ylabel(’rad’); title(’关节3位移变化曲线’);
subplot(3,3,4);plot(t,qd(:,1));grid;xlabel(’t/s’); ylabel(’rad/s’); title(’关节1角速度变化曲线’);
subplot(3,3,5);plot(t,qd(:,2));grid;xlabel(’t/s’); ylabel(’rad/s’); title(’关节2角速度变化曲线’);
subplot(3,3,6);plot(t,qd(:,3));grid;xlabel(’t/s’); ylabel(’rad/s’); title(’关节3角速度变化曲线’);
subplot(3,3,7);plot(t,qdd(:,1));grid;xlabel(’t/s’); ylabel(’rad/s^2’); title(’关节1角加速度变化曲线’);
subplot(3,3,8);plot(t,qdd(:,2));grid;xlabel(’t/s’); ylabel(’rad/s^2’); title(’关节2角加速度变化曲线’);
subplot(3,3,9);plot(t,qdd(:,3));grid;xlabel(’t/s’); ylabel(’rad/s^2’); title(’关节3角加速度变化曲线’);
通过调用函数plot(t,q(:,i))可得到关节变化的位移曲线,调用函数plot(t,qd(:,i))、plot(t,qdd(:,i))可分别得到关节角速度与关节角加速度曲线,如图5所示。由于前3个关节控制机器人末端在空间中的位置,故本文取关节i=1,2,3进行仿真研究。
图5中,3个旋转关节的关节转角都是从初始位置平缓地运动到终止位置,关节角速度都从零平缓地增大到最大值,再逐渐地减小到零,角加速度先正后负说明关节速度先增加后减小,可以发现以PTP运动方式运动的工业机器人在运动过程中的关节位移、角速度、角加速度都没有发生突变的情况,其随时间变化的曲线都较为平滑,说明工业机器人在运动过程中不会出现较大振动,可以很好地代替工人完成作业任务[9]。
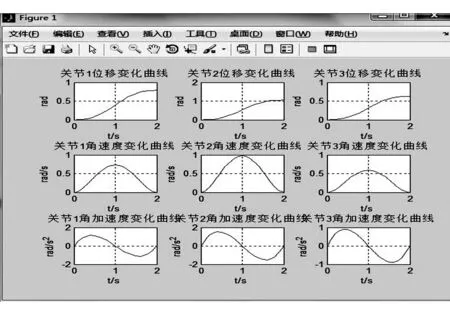
图5 机器人关节角位移、角速度、角加速度变化
5 结论
本文以FANUC R-2000iB工业机器人为研究对象,通过D-H法则建立机器人连杆坐标系与运动学方程,并使用MATLAB软件中的机器人工具箱对D-H法则建立的运动学方程进行了仿真验证,确定了运动学方程的正确性,并对工业机器人PTP运动做了仿真分析,确定了PTP运动的工业机器人的运动较为平缓,可以使用工业机器人完成人们预定的搬运作业任务。
——《李叔同——弘一大师行踪图典》评介

