基于可信度的无线传感器网络高集聚性构造

傅霞玲

(黎明职业大学 教学诊断与质量保证中心,福建 泉州 362000)

因“无所不在”的感知技术以及现代科学技术在微处理传感器性能及体积等方面的进步,无线传感器网络被广泛应用于军事、环境、医疗、家庭及工业商业等领域。然而，由于无线传感器网络采用无线信道及网络拓扑结构的动态变化，使其容易遭受窃听、干扰、入侵等攻击，再加上传感器节点元器件故障、自身能量有限及恶意节点加入等不稳定因素的存在，网络的安全性较差。如何对网络中的传感器节点及链路的可信度进行评价，建立从节点到基站的可信连通链路,保证信息安全可靠地传输到目的节点，提高网络的可靠性和健壮性,是网络设计必须面对的问题。

对此，众多学者进行了相关的研究。邓玮[1]针对无线传感器网络因计算能力差、易被攻击和篡改等问题,提出一种综合考虑影响网络因素的可信路由算法。刘小久等[2]提出了一种基于BP(神经)网络判断节点信息可信度的方法，该方法对采集的多特征值数据进行训练，然后用训练所得结果判断节点可信度，进而筛选出数据。陈蕾等[3]提出采用加密的方式对无线传感器节点间传输的数据进行保护。叶秀彩等[4-6]从提高集聚系数、构造小世界特性这一目的入手构造无线传感器网络，达到节能及延长网络生命周期的目的。本文在这些研究的基础上，综合考虑网络的集聚系数、边的介数和边的连通概率等三方面因素，提出基于可信度的虚拟删边算法，构造基于可信度的高集聚性的无线传感器网络。

1 相关概念

1.1 网络的社团结构

许多实际网络都具有一个共同性质，即社团结构。具有社团结构性质的网络，由若干个“群”或“簇”构成，每个群或簇内部的节点之间连接相对比较紧密，而网络中簇与簇之间的连接却相对比较稀疏，如图1所示。

对于随机撒洒于监测区域的大量传感器节点所构成的网络，同样具有这样的性质，即有的节点连接相对非常紧密，有的连接相对比较稀疏。连接相对紧密的那部分节点，构成网络中的群或簇；连接比较稀疏的，一般是簇间的连接。

图1 网络的社团结构示意图

1.2 集聚系数

集聚系数是网络集团化程度的表现，是网络的一种聚类特性，考察连接在一起的顶点的所有近邻之中有多少是共同的近邻。节点i的集聚系数Ci表示与该节点直接相连的节点之间的连接关系，即与该节点一跳邻居的节点间实际存在的边数目和总的可能存在边数的比例。

1.3 介数

介数分为节点介数和边介数两种。本文使用边介数概念，网络中的边介数表示网络中所有节点对的最短路径中经过该边的数目。正则化表示，假设网络中共有N条不同的最短路径，其中有n条经过该边，则这条边的介数为n/N。介数高的边在网络中体现出较高的重要性和影响力，有较多的最短路径经过该边。

1.4 可信度

可信度又称为声誉评价,广泛应用于电子商务中。交易的双方通过交易后的反馈信息来对双方进行可信度评价，这个可信度评价又将影响以后的交易行为。同样的情况，无线传感网络中的各个节点、边或链路同样具有不同的可信度，必须进行综合考虑及评价。影响网络可信度有多方面的因素，本文用具体的连通概率值来进行衡量，主要是考虑边的连通概率。

1.5 虚拟删边的含义

虚拟删边指的是，在满足网络覆盖度和连通度的前提下，通过功率控制，控制并切断部分符合虚拟删除条件的传感器节点之间的通信链路，节省节点间不必要的通信开销，以达到节能及增强集聚性的目的。

2 网络模型

2.1 模型描述

在节点随机分布的无线传感器网络，节点可以随机分布于规则或不规则的区域中，为研究方便起见，考虑节点随机分布于正方形区域中的情形，并假设：

(1)节点信号传输满足对称性；

(2)无线传感器网络为同构网络，节点的信号传输半径为r，节点具有相同的性能和传输半径。并设e,f为网络中的两个传感器节点，def表示两点间的距离，当def≤r时，节点e,f可以直接通信，则认为e,f节点之间存在一条边；否则，不连边。按照这一原则，对网络进行连边处理，即信号覆盖的范围内两点连边，从而生成网络拓扑图。

2.2 模型分析

初始网络和虚拟删边后的网络拓扑示意图见图2和图3。

图2为传感器节点随机分布的局部拓扑图，网络中信息传输覆盖的范围内两点连线构成网络拓扑图，图中共14个节点，分别用a,b,…，n表示。图3为虚拟删边后网络局部拓扑示意图,其中的节点e,f之间的连边lef、节点h,j之间连边lhj及节点j,k之间连边ljk虚拟删除后的网络拓扑图。删边前及删边后各个节点的集聚系数分别标注于图2、图3上。删边前及删边后平均集聚系数计算如表1所示。

表1 删边前及删边后平均集聚系数比较

由表1知，删边后，网络的集聚系数平均值增大，集聚性增强。并且，由图3可直观地看出，网络更加简化，簇结构更加明显。

3 虚拟删边算法

虚拟删边算法综合考虑集聚系数、边的介数和边的连通概率三方面因素，当一条边符合三方面的条件时，边删除，否则不删除。

3.1 考虑集聚系数

判断一条边是否为候选删除边的方法为，分别判断该边的两个节点是否为候选删除节点，若两点均为候选删除节点，则该边作为候选删除边，等待进行下一步的判断。只要其中一个节点不符合，则该边不是候选删除边。孤立的边不删除，以免产生孤点，造成网络不连通。判断候选删除节点的方法如下。

(1)判断该边一个顶点删除后，集聚系数是否变大。若不变或变小，不删除；若变大，则作为候选删除节点，等待进一步判断。

对于连边lef的两个节点e,f，其中的节点e集聚系数Ce为：

(1)

式中Ee表示节点e的邻节点之间实际相连的边数，Ke表示节点e的度。

设，边lef删除前节点e的集聚系数为Ce，删边后集聚系数为Ce′ ，则：

当Ce′>Ce，节点e为候选删除节点；Ce′≤Ce，不删除。

(2)以同样的方法判断边的另一节点f是否为候选删除节点。

3.2 考虑边的介数大小

若边的局部介数低于某一阈值，例如，低于平均局部介数的n倍，则考虑删边，否则不删边。以边lef为例：

设边lef的局部介数为Blef；两跳邻居范围内平均局部介数为Bav。则：

当Blef≤nBav，考虑删边；Blef>nBav，不删边。

设某条边两端节点各两跳邻居所围成的区域内节点数为m，则计算复杂度为O(m2)。

3.3 考虑边的连通概率

设边lef的连通概率为CPlef，网络的平均连通概率为CPav，则：

当CPlef≤CPav，考虑删边；CPlef>CPav，不删边。

4 仿真及性能分析

仿真采用Visual C++ 开发，500个传感器节点随机分布于800 m×800 m正方形区域内，节点通信半径r=80 m，在信号覆盖范围内的节点间连边生成网络拓扑图。以下的数据为50次运行结果的平均值，仿真结果及实验数据分析如下。

4.1 网络平均集聚系数的比较

图4 为算法作用下，不同的局部介数取值时平均集聚系数增长情况。

图4 不同局部介数取值时网络平均集聚系数增长比率

从图4中可以看出，算法作用下的网络平均集聚系数得到较大幅度的提高，在局部介数取平均局部介数的3倍时，网络的集聚系数增长比率接近32%。在网络得到较好的简化的同时，表现出较高的集聚性。但是，当局部介数取值为平均局部介数的5倍时，此时网络出现不连通的簇。因此，实际应用中对局部介数的取值，需在连通性和平均集聚系数增长比率两者中综合考量，在保证网络连通性的同时使网络平均集聚系数增长比率达到理想值。

4.2 网络平均连通概率的比较

图5为不同平均局部介数取值下，原始网络及算法作用下两种网络平均连通概率的比较。

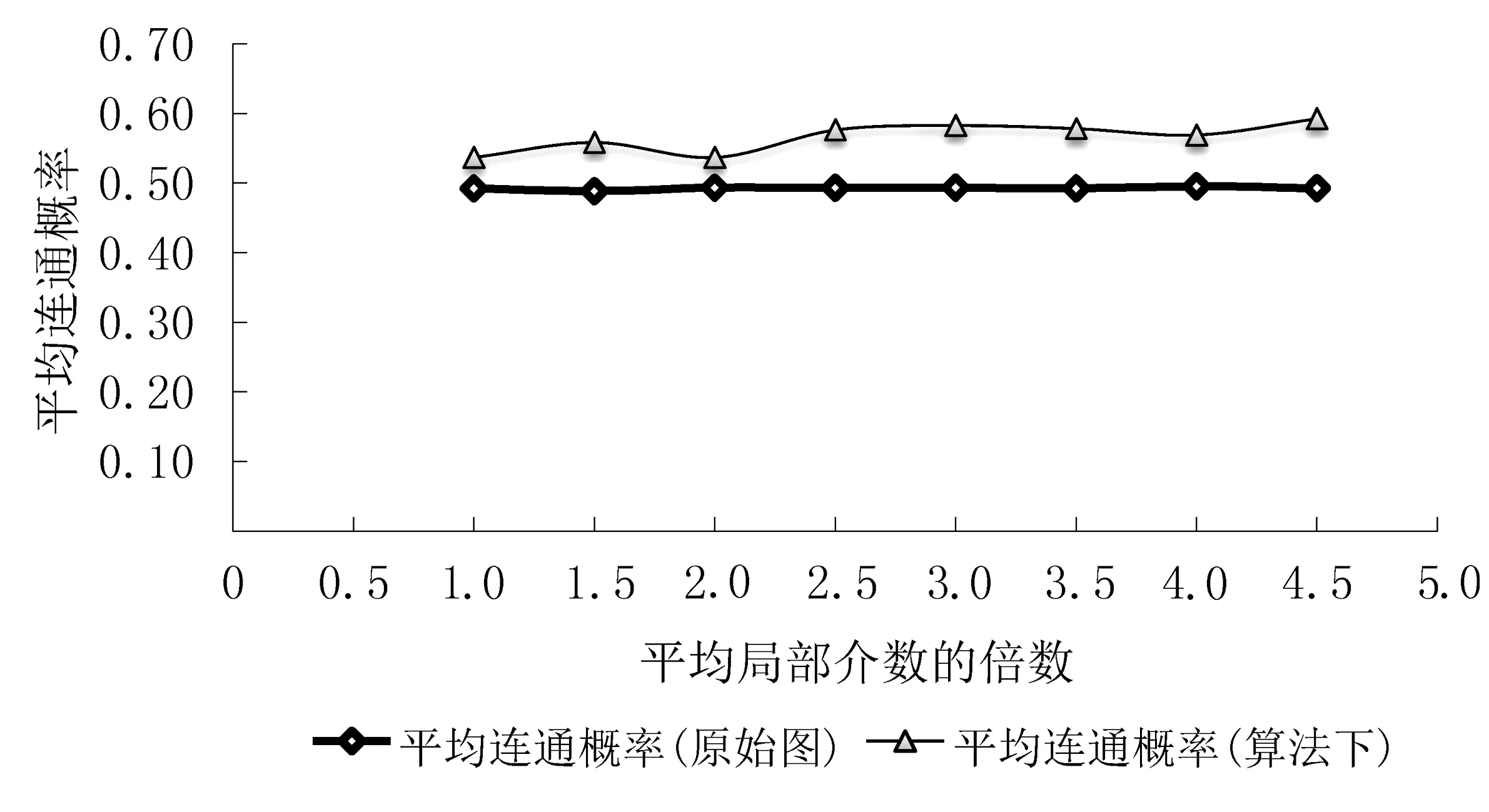
图5 网络连通概率增长比率比较

由图5可见，在算法作用下，网络的平均连通概率大大提高，和原始网络相比，提高近20%。

4.3 原始拓扑图与删边后的拓扑图比较

图6、图7为原始网络拓扑图及局部介数取平均局部介数3倍时，算法作用下所得拓扑图的部分截图。

图6 原始网络拓扑结构图 图7 算法作用下的网络拓扑结构图

将图6和图7进行比较可知，网络的拓扑结构大大简化，簇结构明显，并且能保持全网连通。

5 结 论

理论分析和仿真实验表明，通过本文的算法进行删边后，网络拓扑结构得到简化，簇结构更加明显，网络平均集聚系数得到大幅度提高，表现出更高的集聚性。同时，网络的平均连通概率增幅较大，全网的连通性能更好，网络获得更好的通信质量。