随机算法改进的RCSA-ANN模型及近海短期风速预测

张建平，于新建，陈 栋，纪海鹏

(1. 上海理工大学 机械工程学院，上海 200093；2. 上海电力大学 能源与机械工程学院，上海 200090)

0 引言

风速预测对含大规模风电场的电力系统的安全设计与风险评估具有重要意义[1]。近年来，海上风电场数量逐步增加并且开始并入电网供电，而风电的波动性给电网带来威胁，因此如何准确预测海上风速变得非常重要。

国内外研究人员在短期风速预测上已有些研究，其中人工神经网络（Artificial Neural Network，ANN）模型[2-3]应用较广。潘超等[4]通过极限学习机构建各类别的风速预测模型，结果表明该方法具有较高的预测精度。叶瑞丽等[5]提出了基于小波包分解和改进Elman-ANN的风速方法，计算结果表明，该方法具有更高的预测精度，能够正确反映风速和风电功率规律。Gupta等[6]提出了一种改进布谷鸟搜索算法（Cuckoo Search Algorithm，CSA），从层次模型中提取可用性特征，并在搜索有用特征的基础上找出最优解，在性能上优于原始CSA算法。刘兴杰等[7]提出了基于时空相关性和BP-ANN的风速实时预测方法，并以多个风电场实测数据为例进行仿真测试，结果表明其提出的方法有较高的预测精度。Chen等[8]将长短期记忆ANN与其他模型集成建模，应用于内蒙古某风电场两个案例的研究数据，并与其他常用的预测模型进行对比，验证了该方法具有较好的预测效果。

虽然相关学者在短期风速预测的研究上取得了一定进展，但ANN模型的精度还有待提高，这主要取决于算法寻优性能的高低。布谷鸟搜索算法是一种很有前途的群智能算法[9]，相比于遗传算法、人工蜂群算法、粒子群算法等经典群智能算法，CSA具有更高的搜索效率[10]，其收敛性和全局搜索能力优于粒子群算法和遗传算法，具有较好的参数寻优性能[11]。对于CSA收敛速度偏慢、求解精度较低[12-13]等问题，学者们对该算法开展了较多改进。Makhdoomi等[14]提出了具有自适应混沌感知概率的CSA，仿真结果表明，此算法与遗传算法、粒子群优化算法和原始CSA相比具有更高的精度和鲁棒性。İnci等[15]提出了在系统响应方面有显著改进的动态布谷鸟搜索算法（DCSA），实现了比传统CSA方法更高的工作效率。武小梅等[16]提出一种基于变分模态分解-排列熵和混沌布谷鸟搜索算法优化相关向量机的短期风电功率预测新方法，结果表明，所提出的预测模型能有效提高风电功率预测的准确性。高策等[17]针对CSA列维飞行难以在收敛速度和搜索能力之间的平衡问题，得到了一种改进CSA和支持向量机相结合的陀螺零偏温度补偿方法，实验结果表明，陀螺输出数据误差进一步降低。赵帅旗等[18]研究了CSA算法和自适应变步长的改进扰动观察法并应用到光伏的MPPT控制，通过仿真验证了其方法具有更快的追踪速度和更高的精确度。尽管上述改进解决了CSA部分缺陷，但在求解复杂的多峰优化问题时，如ANN模型的多峰特性[19]，CSA还存在易陷入局部最优解的缺点[15]。风速受多种因素影响，尤其是受当地气象条件的影响较大[20]，一般群智能算法很难优化ANN模型，致使风速预测精度不高，因此亟需进一步改进CSA，提高其参数寻优能力，以期获得更高的预测精度。

基于上述讨论结果，为了提高ANN模型短期风速预测精度，本文通过引入随机因子来改进CSA，利用随机布谷鸟搜索算法（Random-CSA，RCSA）优化ANN模型，从而建立RCSA-ANN海上短期风速预测模型，测得上海芦潮港海上风速与环境参数数据，并对比分析了不同算法训练模型的预测性能。

1 RCSA-ANN建模

1.1 随机算法改进CSA

群智能算法使用的主要机制是随机搜索技术[21]，如禁忌搜索算法、模拟退火算法、遗传算法和粒子群优化，它们均是基于随机搜索[22]和启发式[23]方法来指导搜索模型的最佳参数[24]，相关学者采用随机搜索优化算法取得了良好的效果[25]。因此，本文通过引入随机因子改进CSA得到RCSA，使其随机搜索能力更强，避免了CSA在多峰问题上易陷入局部最优解的不足。

CSA的更新公式可写为[9]：

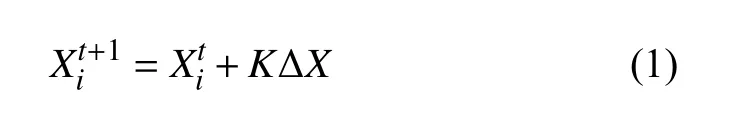
在式（1）中引入随机因子R可 得到改进的CSA，则RCSA更新公式为：

式中，R中 的元素为 [−α,α]之 间的随机数，其中α可根据实际搜索范围的大小来设定。

1.2 ANN模型激活函数

神经网络结构包括输入层、隐含层和输出层。本文选择Sigmoid函数作为隐含层和输入层的激活函数，表达式如下[25]：

则层神经元计算公式为：

式中，Y和X分别为当前层、前一层的神经元，W是这两层之间的权值；B是当前层的偏置。

为了直观显示ANN模型输出风速，输出层激活函数采用如下形式：

式中，λ为极大风速。于是，所采用的ANN模型输出层神经元矩阵计算公式可写为：

需指出的是，这里使用Z(x)函数作为ANN输出层激活函数后，则仅需处理输入数据，省去了训练前后对训练样本数据的处理过程，可使模型训练更加快速。

综上所述，本文通过引入随机因子R改进CSA得到了RCSA，采用Z(x)作为ANN模型输出层激活函数，并利用RCSA优化ANN模型中的权值与偏置参数，从而建立了RCSA-ANN短期风速预测模型。

1.3 模型训练方案

在获得数据集后将其划分为训练集和测试集，采用RCSA对ANN模型进行训练，具体方案如下，流程图如图1所示。

图1 RCSA-ANN模型训练方案Fig. 1 Training scheme of the RCSA-ANN model

1）随机生成模型参数，结合训练集训练RCSAANN模型，训练集共N组且每组包含M种参数，其中环境参数与风速分别作为模型的输入样本与输出样本，训练方案含有两层循环嵌套；

2）内层为以每组数据训练误差最小为目标的循环，利用式（2）对ANN模型的权值与偏置进行更新，循环跳出条件为训练单组数据误差 δ1小 于 ε或循环次数i2大于I2；

3）外层循环为以训练集平均误差最小为目标的循环，若平均训练误差 δ2＞ε 或 循环次数i1＜I1时，则重复1）至2），当外层训练结果满足该层循环条件时训练结束；

4）挑出训练误差最小的模型参数作为RCSA-ANN模型的参数，并通过测试集对模型进行验证，得到验证结果。

2 原始数据与数据处理

2.1 原始数据

通过在上海芦潮港建立的海上测风塔，测得了高度为10 m、时长为230 h的风速、风向、气温与气压四种气象数据，每5 min记录一次，这里将其处理成每小时的平均数据，共计230组，其中包括920个数据点，气象数据绘于图2。

图2 气象参数Fig. 2 Meteorological parameters

2.2 数据处理

由于使用传统归一化方法处理的训练数据难以用来训练模型，因此处理数据时采用如下公式：

式中，xi与x˜i分别为处理前后ANN模型的输入数据；N为训练数据个数。

均 方 根 误 差（Root Mean Square Error，RMSE）εR、平 均 绝 对 百 分 误 差（Mean Absolute Percentage Error，MAPE） εM越小，模型的预测效果越好。因此，可用其来判别RCSA-ANN模型的预测精度，公式分别为：

式中，n为测试集组数；是由ANN输出层预测的第i组的预测风速值；是第i组的实际风速值。

3 芦潮港海上风速仿真预测

3.1 测风数据集划分

由于环境参数用于风速预测效果较好[26]，因此，本文选择气温和气压作为RCSA-ANN模型的输入，风速作为输出，数据集划分情况可见表1。

表1 数据集划分Table 1 Partition of data sets

3.2 模型参数设置

RCSA-ANN短期风速预测模型具有1个输入层、2个隐含层和1个输出层，其中输入层神经元个数为3个，各隐含层神经元均为6个，输出层神经元个数为1个。RCSA随机因子R中 ，α=1，算法种群个体数为3，每个个体均为随机生成的ANN参数矩阵，CSA的参数设置与RCSA中相同。训练参数选择如下：I1=3，I2=25000， ε=2.0×10−3， 训 练 参 数M=3，训练样本组数N=190， 预测样本n=40 ； 即前N组数据用作训练，后n组数据用作测试。

根据文献[27]中的表2.5（风功率密度等级表），10 m高7级风功率密度年平均风速为9.4 m·s−1，则式（5）中的极大风速取 λ=10。

3.3 仿真预测

为了考察RCSA的寻优能力并验证本文RCSA-ANN模型精度，开展了与BP-ANN、CSA-ANN模型预测精度的对比分析。由于改进算法采用随机搜索开展训练，则每次训练后模型预测精度可能有所不同，这里将每种模型分别进行五次训练并预测，以全面考察模型性能，避免模型出现较大的偶然偏差。为了比较每一种模型在各时间点上的五次风速预测的平均值与实测风速的偏差情况，这里给出了基于BP-ANN、CSA-ANN和RCSA-ANN模型预测的风速曲线，分别如图3、图4和图5所示。

图4 基于CSA-ANN模型预测的风速曲线Fig. 4 Wind speeds predicted by the CSA-ANN model

图5 由RCSA-ANN模型预测的风速曲线Fig. 5 Wind speeds predicted by the RCSA-ANN model

由图3可看出：BP-ANN模型在第200 h～220 h内预测精度较差，预测风速随时间变化趋势与实际风速偏离较大，预测值总体偏高，甚至出现与实际风速走势相反的情况，如由该模型第四次训练得到的预测结果（见图3中的BP-ANN4）；在第191 h～196 h与第225 h～227 h时间段，实际风速变化幅度较大，模型预测风速的变化相对平缓。总体来看，BP-ANN模型预测误差较大，这是由于BP-ANN模型采用误差返向传播算法，在更新靠近输入层的参数时，会出现误差梯度为0的情况以致BP算法失效。

图3 BP-ANN模型风速预测曲线Fig. 3 Wind speeds predicted by the BP-ANN model

通过观察图4可以发现：在整个时间范围内，CSA-ANN模型预测的风速随时间的变化规律基本相似；预测的风速大小分布在8.18～9.61 m/s，而实测风速最小值、最大值分别为3.00 m/s、4.94 m/s。预测的风速均明显高于实际风速值，预测误差较大，这是因为CSA-ANN模型尽管使用了与图1相同的训练方案，CSA还是陷入了局部最优，导致ANN模型无法实现风速的准确预测，这也证明了CSA在求解复杂的多峰优化问题时存在易陷入局部最优的不足。

分析图5后不难得知：与BP-ANN、CSA-ANN模型预测结果相比，RCSA-ANN模型的风速预测曲线总体上与实际风速较为接近；在第191 h～197 h时间段内，第一次训练预测的风速（见图5中的RCSAANN1）走势与实际风速吻合度较好，但在204 h后预测值总体上低于实测值；在第194 h～203 h时间段内RCSA-ANN 2与RCSA-ANN 3多数时间点的预测值高于实际风速，但在第204 h～219 h时间段内RCSAANN 2预测精度较高；五个风速预测曲线中，RCSAANN 5预测的风速随时间变化的幅度相对较小，RCSA-ANN 4预测值与实际风速最为贴近。

对比图4和图5后可以得出：在面对多峰特性问题时，RCSA可以避免陷入局部最优，具有更强的搜索能力，克服了CSA的不足；RCSA-ANN模型更能精确地预测芦潮港风速的变化。

为了更加清晰地看出由不同算法训练的三种模型所预测风速曲线的变化，结合图3～图5中预测的风速变化数据，将每一种模型五次预测风速的平均值绘于图6。不难看出：BP-ANN模型预测风速较为接近于实测风速，但在第206 h～221 h时间段内预测偏高于实际值；CSA算法完全失效，导致CSA-ANN模型预测的平均风速与实测风速大小相差甚远；RCSAANN模型预测风速的均值与实测风速的变化趋势基本一致，两者的偏差总体上较小；BP-ANN模型预测效果优于CSA-ANN模型，而RCSA-ANN模型预测精度最高。

图6 每种模型下五次预测风速的平均值与实测值的对比Fig. 6 A comparison of the mean wind speeds between prediction and measurement

3.4 模型精度评价

为了进一步观察BP-ANN、CSA-ANN和RCSAANN模型的预测精度，这里计算了三种模型预测风速的均方根误差和平均绝对百分误差，分别列于表2与表3。

表2 三种模型的均方根误差Table 2 Root-mean-square errors of three models

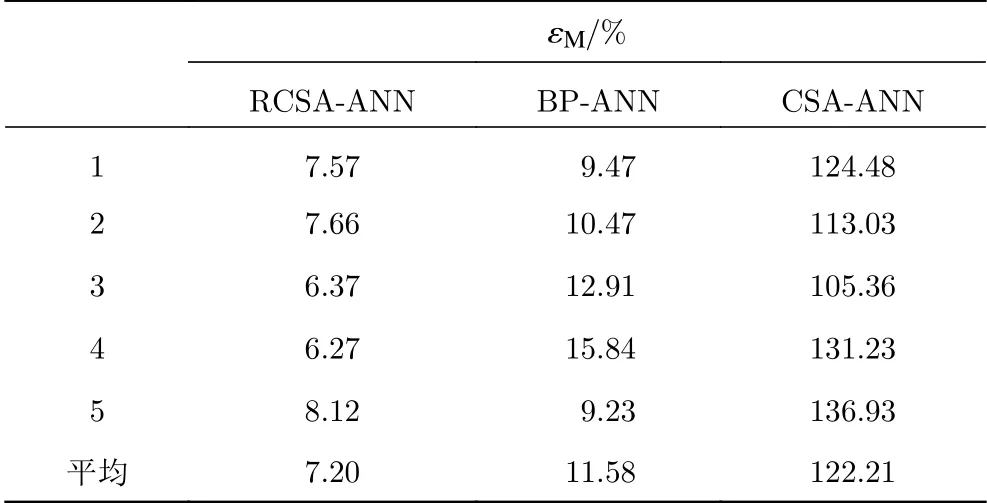
表3 三种模型的平均绝对百分比误差Table 3 Mean absolute pertentage error of three models

通过分析表2可得：CSA-ANN模型预测的平均均方根误差为4.91 m/s，远高于BP-ANN的0.58 m/s，而RCSA-ANN模型的最低，仅为0.40 m/s；与BPANN、CSA-ANN模型相比，CSA-ANN模型五次预测的最低 εR分 别降低了29.17%、91.98%，最高 εR分别下降了41.03%、91.65%，平均 εR分别减少了31.03%、91.85%。上述数据表明了CSA-ANN、BP-ANN、RCSAANN模型预测风速的均方根误差依次降低。相比于其他两个模型，RCSA-ANN模型的预测准确度均得到明显提升，且相对于CSA-ANN模型的提升幅度更大。

根据表3可知：CSA-ANN模型每次预测的平均绝对百分误差均超过100%，最高为136.93%，说明训练该模型的算法已失效；RCSA-ANN模型最大 εM仅为8.12%，而BP-ANN模型最小 εM却达到9.23%，意味着BP-ANN模型的预测精度相对较低；CSA-ANN、BP-ANN、RCSA-ANN模型的平均 εM分别为122.21%、11.58%、7.20%，表明RCSA-ANN模型具有最高的预测精度。

4 结论

本文利用随机因子对CSA进行改进，得到了RCSA-ANN模型，测得了芦潮港海上气象数据，开展了模型训练，完成了短期风速预测与分析。得到的主要结论如下：

1）改进的RCSA具有较强的搜索性能，能较好地解决多峰特性寻优问题，可推广应用于其他群智能算法；

2）设计的RCSA-ANN模型训练方案切实可行，得到的RCSA-ANN模型参数准确可靠；

3）RCSA-ANN模型预测海上风速的效果良好、精度较高，可为海上风速实时预测系统提供参考。