数学史融入勾股定理的教学设计
⦿重庆师范大学 陈星羽
1 教学过程
1.1 创设情境,导入新课
师:请问同学们竹竿能不能横着(保持与门框所在的面平行)拿到教室里?如果能,那竹竿的长度最长不得达到多少才能拿到教室?如果要想办法解决这个问题,我们就开始今天的学习吧!
设计意图:用现实生活中的问题很自然地引出新课程,同时也反映了数学来源于生活,并应用于生活.
1.2 探索定理——自主操作,引导探索
1.2.1 探究等腰直角三角形三边的关系

图1
师:大家在日常生活中有没有遇到过这种形状(如图1)的地板?它其中包含哪些我们已经知道的基本图形呢?
生:正方形、三角形、等腰直角三角形.
师:对,我们也很容易看出这块地板是由等腰直角三角形组成的.请问地板上A,B,C三个正方形的面积存在什么关系?根据这些关系,你能够推测出由A,B,C三个正方形围成的等腰直角三角形的边还存在什么样的关系吗?
生:等腰直角三角形两条直角边的平方加起来正好等于第三条边的平方.
设计目的:通过学生所熟悉的生活案例以及生活中的问题有效激发学生们的求知欲,充分利用学生的好奇心.
师:其实早在2500年前,古希腊著名数学家和哲学家毕达哥拉斯已经发现了这个结论,让我们一起来看看他是怎么发现的吧.(PPT当中设计超链接,点击该链接播放相应的视频.)今天大家也通过自己的观察总结出:等腰直角三角形两条直角边的平方加起来等于第三条边的平方.如果大家早出生2500年,说不定今天的这条定理就是以各位同学的名字来命名的.所以我们要善于发现、思考生活中的各种现象,而这种看起来平淡无奇的自然现象有时却蕴含着深奥的数学道理.
设计目的:对学生的学习兴趣予以正向激发,培养学生的上进心,帮助其树立正确的学习观,建立自信心.
1.2.2 探索一般直角三角形的三边之间的关系
师:等腰直角三角形有上述性质,其他的直角三角形也有这个性质吗?如图2,在方格网中作一个不等腰直角三角形ABC,再以此三角形的各边为边,作正方形(Ⅰ,Ⅱ,Ⅲ).请问三个正方形面积SⅠ,SⅡ,SⅢ分别是多少?你们发现直角三角形三边的长有怎样的关系呢?请大家按之前分好的小组进行讨论,讨论时间为8分钟,讨论结束后请小组代表起来作答.

图2
(学生作答方法总结如下.)
方法1:割.

图3
如图3,正方形Ⅰ的面积为9个单位面积、正方形Ⅱ面积为16个单位面积.把正方形Ⅲ分割为五部分,共包含一个小正方形还有四个直角三角形,那么正方形Ⅲ的面积共计25个单位面积.
方法2:补.
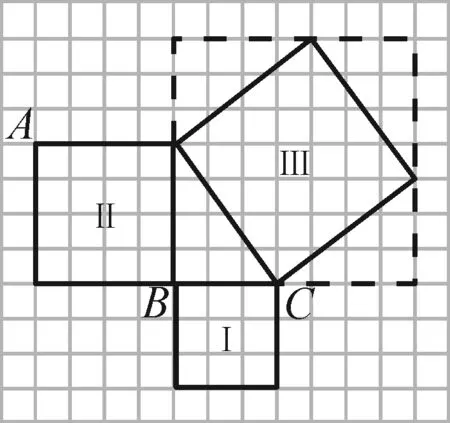
图4
如图4,在正方形Ⅲ的四周画出四个完全一样的直角三角形,补成一个大正方形,同样正方形Ⅲ的面积为25个单位面积.
通过上述推导过程可知:以直角三角形两个直角边为边长的正方形面积加起来正好等于以斜边为边长的正方形的面积,推出直角三角形两条直角边的平方和等于斜边的平方.
设计意图:以小组讨论的形式组织学生学习可以极大地调动学生的学习热情,通过良好的课堂氛围让所有学生积极地参与到课堂当中,确保学生在课堂中占据绝对的主体地位,有利于学生发散性思维的形成.通过学生操作、教师提出问题、学生猜测、教师动画演示等师生互动环节,得出三边关系,滲透割、补、拼等求面积的方法,为引入勾股定理的面积证法作铺垫.

图5
师:请同学们继续思考如果用a,b,c三个字母分别表示三角形的三边(如图5),那么我们可以得出什么结论呢?
生:a2+b2=c2.
师:这就是本节课的重点,即勾股定理.如果a,b,c分别表示直角三角形的三条边,a,b表示直角边长,c表示斜边长,那么a2+b2=c2.
设计意图:本节课的数学思想为归纳推理思想,由数字特例推广至字母,引导学生直观感受由特殊到一般.把新问题转化为已解决的旧问题来解决,从数与形两种角度观察、思考、比较,并从中了解问题的实质.对学生的综合性思维、归纳能力以及自主学习能力予以有效的培养.
师:早在西汉末年的古书《周髀算经》当中有清晰的记录:公元前1 120年古人就已经总结出“勾三股四弦五”,翻译过来就是在直角三角形当中,倘若勾等于3,股等于4,则弦肯定等于5.所以,在我国称它为勾股定理.那为什么又叫毕达哥拉斯定理呢?因为我们的祖先并没有从这一个特例发现所有直角三角形三边之间的特殊关系,所以这一定理的名称就让给了毕达哥拉斯.
设计意图:让学生了解勾股定理名称由来的同时激发学生的学习热情和民族自豪感.
1.3 初步应用
基础题如图6所示,分别求出下列Rt△ACB中未知数对应边的长度.

图6
情境题已知我们教室的门宽1m,高2m,我拿进教室的竹竿长1.5m.请问竹竿能不能横着(保持与门柜所在平面平行)拿进教室?竹竿的长最长不能超过多少?
探索题《风动莲花》:波平如镜一湖面,半尺高处出红莲,鲜艳多姿湖中立,猛遭狂风吹一边;红莲斜卧水淹面,距根生处两尺远;渔翁发现忙思考,湖水深浅有多少?[1]
设计意图:根据学生发展的不均衡,进行因材施教.基本题注意双基,培养学生的数学兴趣;情境题则体现数学来源于生活,并服务于生活;探索题重在开阔学生思路,培养学生的创新精神,同时培养学生的数学史素养.
1.4 回顾小结
本节课你收获了什么?
设计意图:通过小结,帮助学生梳理知识,加强知识点联系,从整体把握勾股定理.
1.5 布置作业
基础题(必做):课本第24页练习1~2题,第28页习题1~2.
拓展题(选做):利用上网等方法查询勾股定理的证明方法,并写出研究性学习报告.
2 结语
将中西方勾股定理的数学史融入教学,以故事的形式,把知识传授给学生,使学生能够更加容易接受知识以及加深对知识的理解.通过多媒体播放毕达哥拉斯如何发现勾股定理,以及介绍《周髀算经》的“勾三股四弦五”来提高学生的数学史素养.课堂练习环节也将数学史融入习题中,巩固勾股定理知识的同时,让学生保持学习的激情.同时,拓展题的设计,让学生课后查阅勾股定理的证明方法,在拓展课堂知识的同时,丰富学生的数学史.

