一类定边对定角问题的解法探究
⦿安徽合肥一六八陶冲湖中学 武前炜
1 引言
三角形中的有关线段计算是平面几何常考试题,常常利用勾股定理、相似性质或三角函数来计算,不同的方法计算难易程度不一样.
2 解法探究
下面通过两个例题对定边对定角问题进行解法探究.

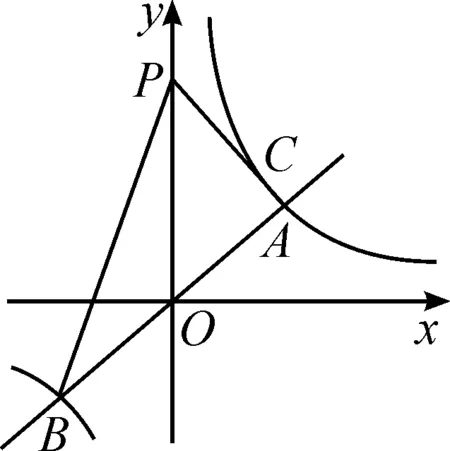
图1

图2

解法1:(一线三等角相似)如图2,在y轴上分别取点M,N,使得∠AMO=60°,∠BNP=120°,由“一线三等角”可得△APM∽△PBN.分别过点A,B作y轴垂线,垂足为点E,F.

ME=NF=1,AM=BN=2.
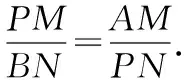

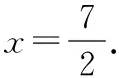

解法2:(三角形面积)设点P(0,y),y>0.
由距离公式可得,
根据三角形铅锤公式面积计算,得
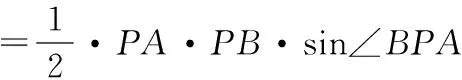

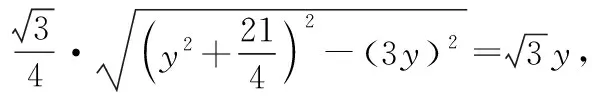


解法3:(辅助圆)先来看基本图形,如图3,△ABC中,定边AB所对的∠C为定角α.

图3

图4
由图形定边对定角,考虑△ABC外接圆⊙O,如图4,根据圆周角性质可知∠AOB=2α,于是问题转化为在等腰三角形AOB中来解决.特别地,一些题目中α取一些特殊角度,从而△AOB为特殊的等腰三角形,极大地方便后续计算.
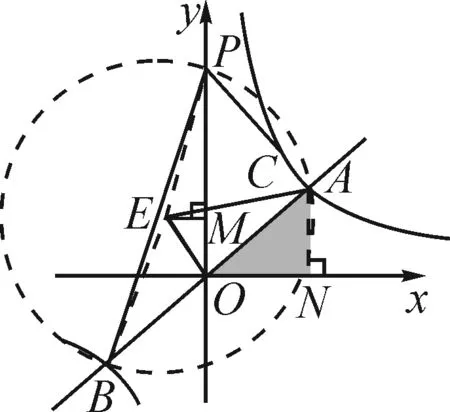
图5

根据反比例函数的对称性可知,点O为线段AB的中点,从而

过点A作AN垂直于x轴,垂足为点N,过点E作EM垂直于y轴,垂足为点M.
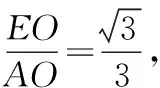

在Rt△EMP中,由勾股定理得
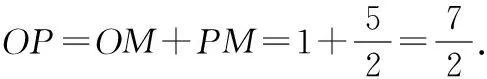

解法4:(正切和角公式)站在高中视角下,本题无需构造,直接列式建立等量关系计算.
如图6,分别过点A,B向y轴作垂线,垂足分别为点E,F.

设∠BPO=α,∠APO=β,则α+β=60°.

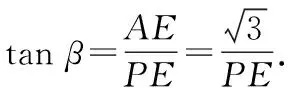

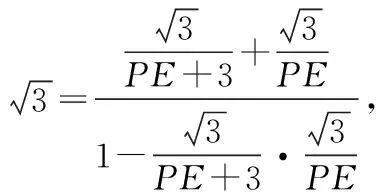


图6

图7
拓展:初中生通过构造三角形相似可以进行正切和角公式的推导.如图7,在矩形ABCE中,点D在边EC上,点F在边AE上,且FD⊥BD,连接BF,∠FBD=α,∠DBC=β.
不妨设DE=1,则EF=tanβ.





评析:合理联想与构造是一种重要的数学解题能力,也是平面几何魅力所在.解题后要善于总结归纳,而不应停留在题目本身,多琢磨其结构,多反思其用途与变化,使其成为今后解题的工具.
例2如图8,在△ABC中,∠BAC=135°,AD⊥BC于点D.若BD=6,CD=20,则线段AD的长度为______.

图8

图9
解法1:(构造45°等腰直角三角形)由∠BAC=135°可知其补角为45°,联想构造45°的等腰直角三角形.如图9,过点C作AC的垂线交BA延长线于点E,再过点E作BC的垂线交BC于点F.则出现“一线三直角”的全等结构△ADC≌△CFE(AAS),从而可得AD=CF,EF=CD=20.
设AD=a,则CF=a.
由AD∥EF,知△BAD∽△BEF.
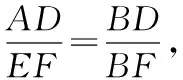
解得a=4(负值舍去).
即AD=4.
解法2:(对称法)由∠BAC=135°,可知∠B+∠C=45°.如图10,分别沿着AB,AC将△ABD,△ACD对称至△ABE,△ACF,延长BE,CF交于点G.易知∠GBC+∠GCB=90°,即∠G=90°.
根据对称性质,可得
BE=BD=6,CF=CD=20,
AE=AD=AF,
∠GEA=∠GFA=90°.
从而得出四边形AEGF为正方形.
不妨设AD=a,则AE=AF=GE=GF=a.
在Rt△BCG中,由勾股定理得
GB2+GC2=BC2.
即(6+a)2+(a+20)2=262,得a=4(负值舍去).
所以AD=4.
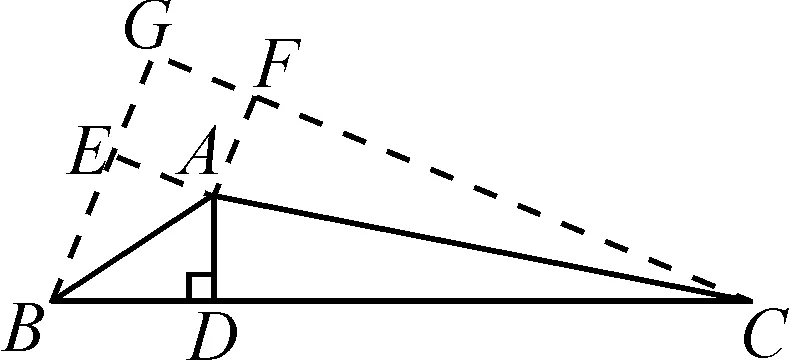
图10
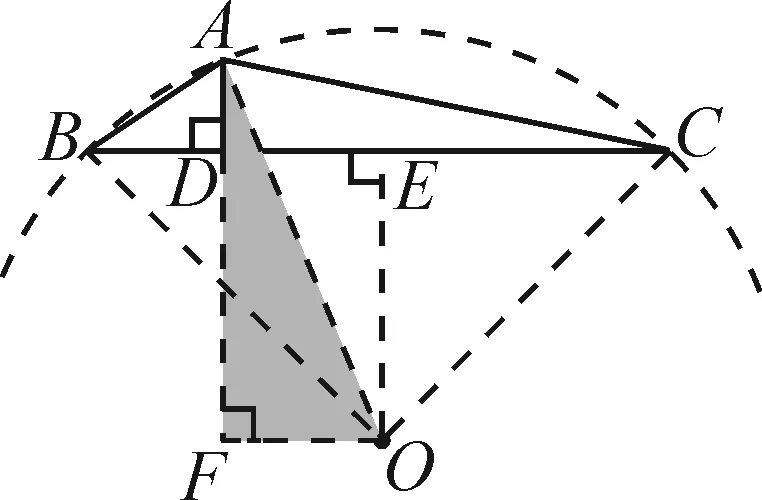
图11
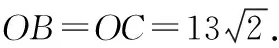
过点O作OE⊥BC,E为垂足,则
过点O作AD的垂线交AD的延长线于点F,可得矩形OEDF,从而DF=OE=13,OF=DE=7.
在Rt△AOF中,由勾股定理得
AF2+OF2=OA2.

解得AD=4(负值舍去).
解法4:(正切和角公式)

由正切和角公式知

解得AD=4(负值舍去).
以上两例的前三种解法都属于构造法,构造后的图形是平时常见的基本图形.中考题中的一些“难”题有意识地考查学生分析问题和解决问题的能力,这就要求学生在平时的解题训练中,注重反思积累,也需要教师有意识地选择典型题目作为素材,挖掘图形结构,归纳总结通性通法.不仅要认识基本图形,了解其蕴含的关系,更要熟悉基本图形的结构特征.往往一些考题将其一部分隐去,增加了思维难度,需要观察后进行合理联想、尝试,从而让解法自然生成.对于几何问题,“几何直观”是直达“学生最容易想到或者适合最近发展区的解法”的重要途径.所以在分析问题的过程中,学生若能从几何直观出发挖掘出题目中的隐含条件,则问题“柳暗花明”.
3 结语
张景中先生认为:“一种方法解很多题,要好过很多方法解一道题.”这里的“一种方法”绝不是技巧性强、灵机一动的妙法,而应是最基本、最自然的通法.站在数学思维的角度,自然的解法才是最好的方法,因为自然的解法才是学生能想到的方法.上述两例的几种构造解法都很巧妙,其中作辅助圆属于通法,由定边定角联想辅助圆,这应该成为师生认知共鸣的方法,只有这样才能更好地培养学生思考问题和探究问题的能力.

