引入注意力机制的AdaBoost算法

缪泽鑫，张会生，任 磊

(1. 大连海事大学信息科学技术学院，辽宁 大连 116026；2. 大连海事大学理学院，辽宁 大连 116026)

1 引言

AdaBoost是一种重要的集成学习算法[1]。它首先从弱学习算法出发，通过反复学习得到一组弱分类器，最终将弱分类器组合成强分类器。其思想是：对于复杂任务而言，将多个专家的判断进行适当综合而作出的判断，往往要比其中任何一个专家的单独判断好。AdaBoost有很多良好特性：首先弱分类器权重可以通过计算得到而非人工调整；其次在数学上可以证明随着训练次数的增加，训练误差以指数速率下降[1]。正因如此，它已被广泛应用于人脸识别、目标检测等领域。AdaBoost的学习过程可以分成三个步骤：①找到若干个误差相互独立的弱分类器；②训练得到弱分类器的权重；③弱分类器合并得到最终的强分类器。

2 相关研究

廖红文等人[2]对AdaBoost及其改进算法进行综述，他们介绍了AdaBoost算法在权值更新方法上的研究进展，指出原始AdaBoost算法在弱分类器权重和样本权重的训练问题上存在缺陷。

从数学上看，AdaBoost的弱分类器参数的设定可以看作函数空间中的梯度下降算法[3]，它在每一步选择与负梯度下降方向最接近的分类器作为下降方向,并用精确线搜索确定下降步长。这种计算方法本质上是一种贪心算法，即只根据当前样本的分布来搜索使得误差下降最快的方向和步长，但在全局上并不一定能保证最优。针对该问题，蒋焰等人[4]认为训练样本的分布不仅与当前分类器有关，而且也需要考虑前面的若干分类器。他们进而提出的新算法在每一个分类器集成进来后会对前面产生的某些分类器权重进行修正，所以前面训练好的弱分类器的权重不再是固定值，而会根据整体性能进行调整。

从实际问题出发，李闯等人[5]指出弱分类器的加权参数不但与错误率有关，还与其对正样本的识别能力有关，并在此基础上提出AD AdaBoost算法。该算法采用更为有效的参数求解方法，使其在目标检测问题上具有更好的效果。Richard Machlin[6]认为后来的分类器更关注于之前没有被正确分类的样本，因此可以猜想到之后的分类器在某些类别的样本上表现很好，而在其它类别的样本上表现一般。所以对于一个分类器来说，不考虑其对样本擅长处理与否而使用相同的权重，是不合理的。针对该问题，其提出的RegionBoost算法能对弱分类器权重进行动态调整。

在样本权重的调整问题上，对多次分类错误的样本，弱分类器会不断增加其权重进而导致过拟合。针对该问题，Allende等人[7]提出了RADA算法，通过对误分类样本的权重作阈值限制，有效解决了误分类样本权值偏高的问题。Yunlong[8]提出的EAdaBoost算法则先用KNN剔除噪声样本再进行样本训练。

不同于上述分别单独从样本的权重调整或弱分类器的权重调整的角度对AdaBoost开展的研究，本文考虑将样本和弱分类器的权重优化纳入统一框架，提出引入注意力机制的AdaBoost算法。这里注意力机制的思想是：对于损失函数的优化而言，每一个样本和分类器所提供的贡献是不同的，因此可利用神经网络强大的自学习能力，为样本和弱分类器的重要程度自动打分。此模型不仅通过对损失函数引入关于样本权值的L2正则项来控制错分类样本权重的过分增长，而且为弱分类器的动态调整问题提供了除多步校正算法[4]外的另一途径。

3 AdaBoost算法流程

AdaBoost算法的具体流程[1]如下：

设训练数据集T={(x1，y1)，(x2，y2)，…，(xN，yN)}，其中xi∈X⊆Rn，yi∈Y={-1，+1}。初始化训练集的权重分布

对m=1，2，…，M

(a)使用具有权值分布Dm的训练数据集学习，得到基本分类器

Gm(x)：X→-1，+1

(b)计算Gm(x)在训练数据集上的分类误差率

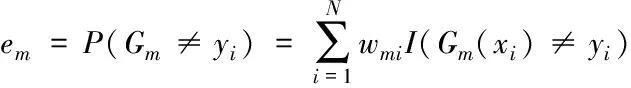
(1)

(c)计算Gm(x)的权重系数

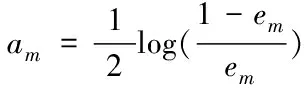
(2)

(d)更新训练数据集的权值分布

Dm+1=(wm+1，1，…wm+1，i，…，wm+1，N)

(3)

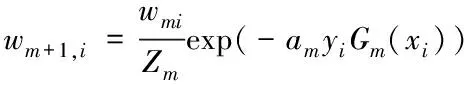
(4)

这里Zm是规范因子，

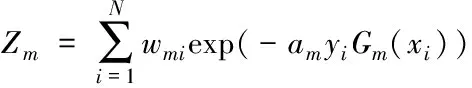
(5)

得到基本分类器

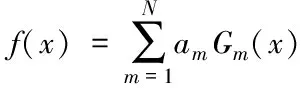
(6)

和最终的分类器

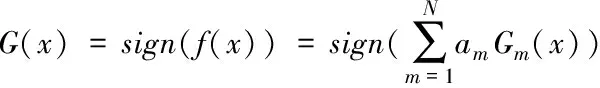
(7)

其中sign(f(x))是使得结果为1或-1的符号函数。

4 引入注意力机制的AdaBoost模型

机器学习中的注意力机制[9]源自于人类视觉的注意力机制：将有限的注意力集中在重点信息上，从关注全局到关注重点，从而节省资源，快速获得最有效的信息。从注意力机制的实现角度，可将其理解为一种权重参数的分配机制，目标是协助模型捕捉重要信息。

目前注意力机制已经应用到越来越多的领域，如在机器翻译[10]中引入注意力机制，只关注与当前状态有关的上下文，提高了翻译系统的准确度。在推荐系统方面，通过在原始的FM模型[11]上加上一个注意力层来自动调节二阶特征的权重，AFM模型[12]相比FM模型提高了预测准确度。

引入注意力机制的AdaBoost模型结构如图1所示，其中第一个注意力层用来为样本打分，第二个注意力层为弱分类器打分后输出损失函数。定义损失函数

(8)

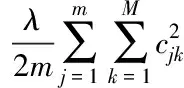
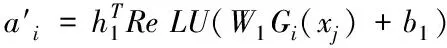
(9)

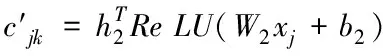
(10)

其中h1、h2分别是两个神经网络的全连接层到softmax输出层的权重向量，W1、b1分别是弱分类器到神经网络全连接层的权值矩阵和偏置向量，W2、b2分别是样本到神经网络全连接层的权值矩阵和偏置向量。通过softmax层归一化后样本和弱分类的注意力得分为

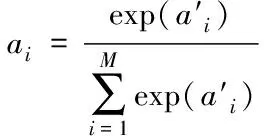
(11)

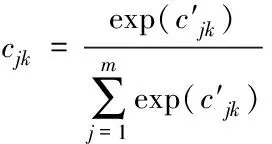
(12)

模型的具体执行过程如下：首先随机初始化样本和弱分类器的得分，并将样本输入到第一个注意力网络层中，样本经过注意力层得到新的得分后输入到第一个弱分类器中，弱分类器对样本预测后输入到第二个注意力层中得到损失函数。利用随机梯度下降法最小化损失函数来反向更新样本和弱分类器的注意力得分。当第一个弱分类器训练结束后将样本输入到第二个弱分类器中，而在第二个弱分类器训练时综合考虑当前弱分类器和之前弱分类器的损失，即

floss=f第一个弱分类器的损失+f第二个弱分类器的损失

(13)

并重新更新第一个弱分类器的得分。第一个弱分类器在第二次训练时只更新弱分类器得分而不改变之前样本在其上的得分，这样保证了样本在不同弱分类器上采用不同的得分。之后每次均采用相同方式更新弱分类器得分。同理在计算第n个弱分类器的注意力得分时会结合之前n-1个弱分类器的损失并更新前n-1个弱分类器的注意力得分。传统的 Adaboost 算法在训练弱分类器时每一次都是由贪心算法来获得局部最佳弱分类器权重，不能确保全局最佳。而本文考虑了整体性，认为新加入的弱分类器会对之前的弱分类器权重产生影响，所以当加入了新的弱分类器后会结合之前所有的弱分类器重新训练，最终求得一组最优的弱分类器权重。模型参数的学习借鉴了GAN[13]网络的训练方式，分为两个过程。首先固定后半部分，先训练样本的权重，当样本权重收敛后固定前半部分，再训练弱分类器的权重。

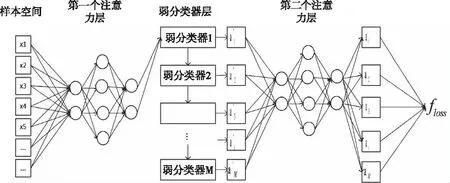
图1 引入注意力机制的AdaBoost模型

5 L2正则化对样本权重的影响

在(8)式中，在损失函数中引入了L2正则项，下面简要分析该正则化方法对样本权重的影响。为方便表述，将(8)式改写为

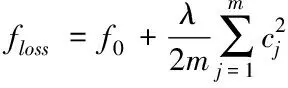
(14)

其中

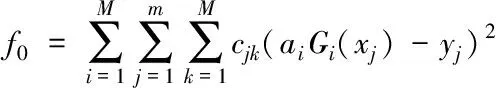
(15)

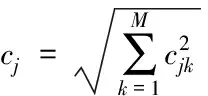
(16)

由于采用随机梯度下降法更新参数，对损失函数关于参数cj求偏导可得

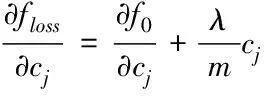
(17)

此时权值的更新公式变为

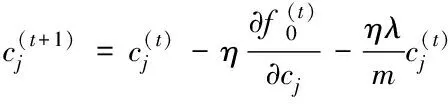
(18)

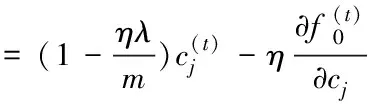
(19)

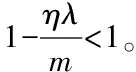
6 实验

6.1 实验数据集和环境

实验数据集分别来自Kaggle的Titanic[14]、信用卡欺诈[15]和员工离职率以及科赛网的银行精准营销解决方案[16]，数据集的具体统计信息如表1所示。实验在表2所示的实验环境中完成。

表1 实验数据集

表2 实验环境及配置

6.2 实验对比和分析

通过数值实验将本文算法与动态调整权重算法(MSC-AdaBoost)[4]、RegionBoost[6]以及对样本作阈值限定的RADA-AdaBoost[7]算法作对比。本文算法采用Cart作为弱分类器，设置最大迭代次数为100。注意力层采用ReLU函数作为激活函数。取各数据集前75%的样本作为训练集，后25%作为验证集。首先尝试将本文算法的正则项系数设置为0。表3对比了不同隐藏层个数对模型的影响。从表3可以看出，随着网络层数增加算法的准确率不断上升，在n=3时本文算法在所有数据集上已经优于文献中算法。由于n=4时与n=3相比准确率提升较小，但是会额外增加较大计算量，所以接下来的实验都取三个隐藏层。通过网格搜索找到本文算法在四个数据集上的最优正则项系数分别为：0.4，1.2，6.4和3.2，对应的准确率分别为：0.8274，0.9301，0.9524和0.8704。由此可以看出，相比于原始没有正则项的算法，加入了正则项之后算法准确度有了一定提升。图2到图5绘制了随着弱分类器个数的增加四种算法在正则项系数最优情况下的误差变化曲线。从图中可以看出本文算法的性能整体上优于其它三个改进的算法，从而验证了其有效性。

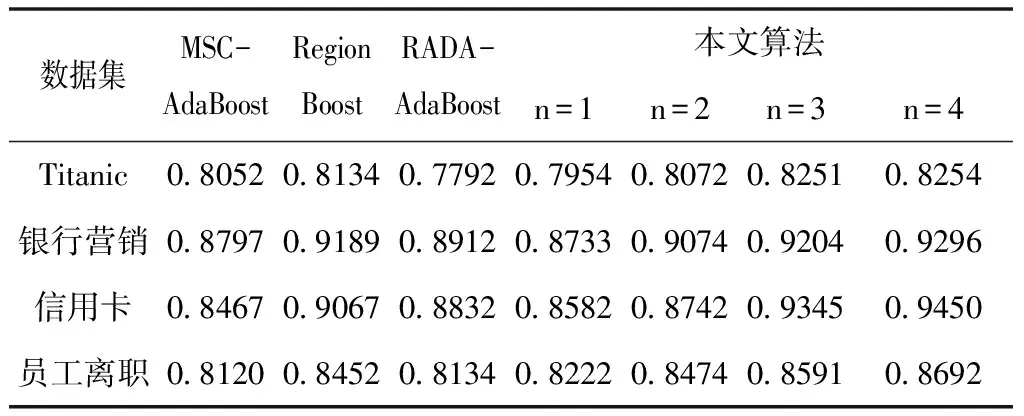
表3 不同网络层数四种算法的对比

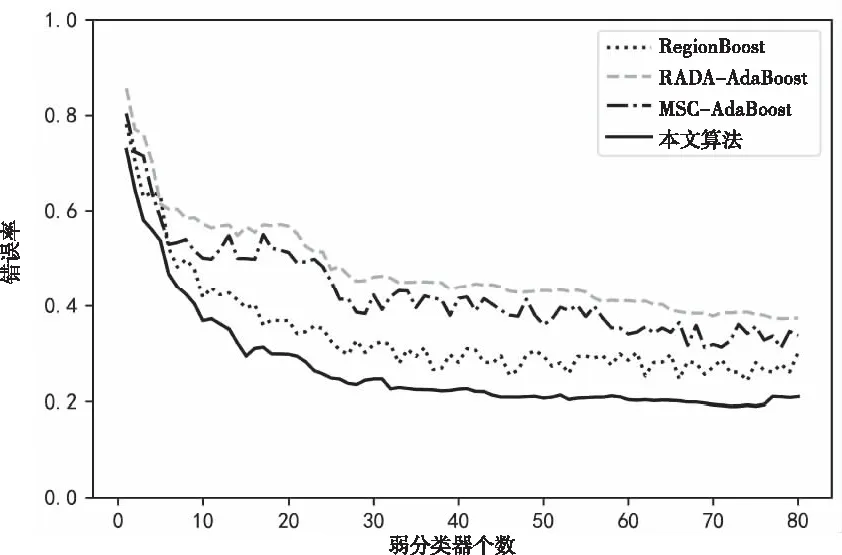
图2 Titanic数据集下四种算法的性能对比

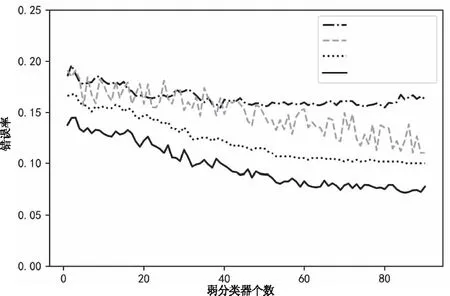
图3 信用卡欺诈数据集下四种算法的性能对比

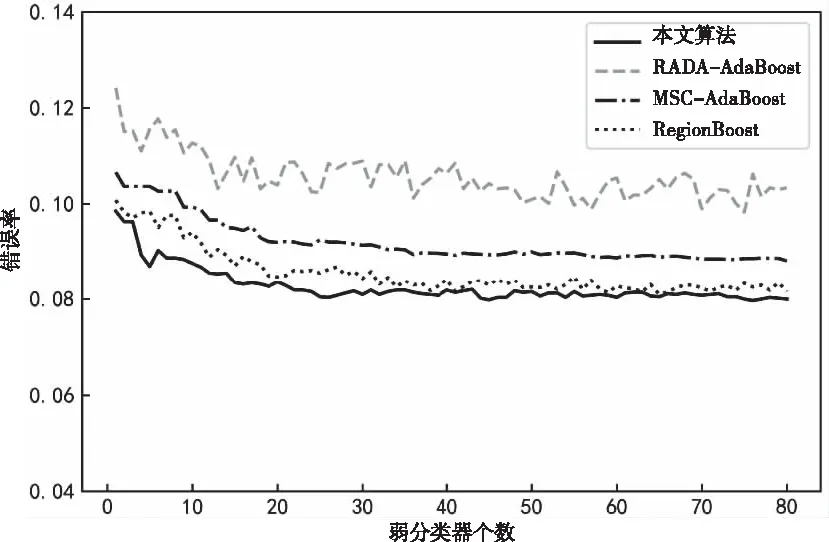
图4 银行精准营数据集下四种算法的性能对比

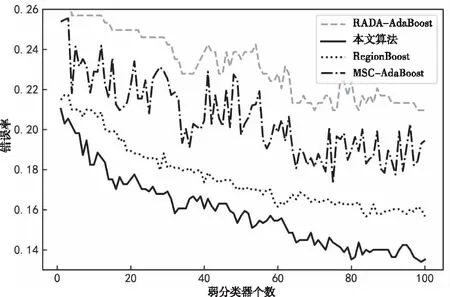
图5 员工离职数据集下四种算法的性能对比

7 结束语

针对AdaBoost算法的弱分类器权重无法动态调整以及对多次分类错误的样本设置过高权重这两个缺陷，本文提出了结合注意力机制的改进算法，通过引入两个注意力层，利用神经网络分别为样本和弱分类器的重要程度打分，实现了弱分类器权重的动态调整，并结合L2正则化方法有效控制了错分类样本权值的大小，数值实验验证了所提算法的有效性。未来工作包括如何将深度学习和打分机制结合来进一步提高算法性能以及将此算法推广应用到多分类任务中去。