基于改进Bootstrap-Bayes的电子式剩余电流动作断路器可靠性评估

刘帼巾 王 泽 李 想 赵兴洲 缪建华

基于改进Bootstrap-Bayes的电子式剩余电流动作断路器可靠性评估

刘帼巾 王 泽 李 想 赵兴洲 缪建华

（省部共建电工装备可靠性与智能化国家重点实验室（河北工业大学） 天津 300130）

作为一种高可靠性、长寿命产品，电子式剩余电流动作断路器可获得的试验数据很少。为了对其可靠性进行评估，提出一种基于改进Bootstrap-Bayes的可靠性评估方法。首先，进行温度为加速应力的剩余电流动作断路器的加速退化试验，利用退化数据外推得到伪失效寿命，经检验，电子式剩余电流动作断路器伪失效寿命服从双参数威布尔分布；然后，采用灰色GM(1, 1)模型对试验数据进行扩充作为先验信息，通过马尔科夫链蒙特卡洛（MCMC）算法中的Gibbs抽样结合Bayes公式得到参数估计值；最后，利用Arrhenius加速模型实现正常使用环境下剩余电流动作断路器的可靠性评估。

电子式剩余电流动作断路器 GM(1, 1)模型 Bootstrap抽样 Bayes MCMC 可靠性评估

0 引言

剩余电流动作断路器是一种常用的低压保护电器，在保护用电人员人身安全及防止漏电事故方面具有重大作用[1-2]。电子式剩余电流动作断路器制造过程简单、生产成本较低，已成为我国剩余电流动作断路器的主流产品。电子式剩余电流动作断路器在使用过程中性能逐渐退化甚至失效。因此，对其进行可靠性评估，在失效前及时采取措施，能够有效提高低压配电系统的可靠性和安全性[3-4]。

目前，低压电器等产品的可靠性评估及寿命预测已成为研究的热点[5-6]。当前的研究大多集中于基于神经网络[7-8]、Wiener过程[9]、Gamma过程[10]、支持向量机[11-12]等方法的评估预测。以上各种方法中，神经网络进行训练时需要的样本数据较多，例如：文献[7-8]训练数据长度分别为2 500和799，并且预测结果受样本容量影响较大；基于Wiener过程和Gamma过程建模分析时退化量需要满足特定的分布形式；支持向量机在处理小样本数据问题时具有一定的优势，但其预测的准确性受参数影响较大，优化的过程较为繁琐。从样本容量、计算量、建模及求解过程方面考虑，Bayes方法常用来解决小样本可靠性分析问题，能够有效减少试验所需次数、缩短试验时间、节约试验成本。剩余电流动作断路器可靠性高、寿命长，退化过程缓慢，短时间内难以获得足够的试验数据，因此，本文选择利用Bayes方法对剩余电流动作断路器的退化过程进行分析。

Bayes方法先利用先验信息确定参数的先验分布，再综合先验信息和试验数据得到参数的后验分布[13-14]。在 Bayes方法中，参数先验分布的确定十分重要，将直接影响最后结果的准确度。当前，参数先验分布的确定方法主要有共轭先验分布[15]、主观概率法[16]、无信息先验分布[17]和Bootstrap抽样法[18]。上述确定方法中，共轭先验分布具有一定的使用范围，并不是所有模型参数都有相应的共轭先验分布；主观概率法因主观因素使得预测结果误差较大；无信息先验分布中Bayes假设的使用必须满足一定的前提条件；Bootstrap抽样法通过反复抽样扩大样本数量，在分析小样本问题的可靠性中有很强的适用性，但在无先验信息时不适用。Bayes方法的后验分布求解涉及到高维积分运算，计算过程复杂且速度缓慢。

本文提出一种改进的Bootstrap-Bayes可靠性分析方法，针对先验分布确定方法中存在的一些不足，利用GM(1,1)模型扩大Bootstrap抽样法确定先验分布的适用范围，使Bootstrap-Bayes法在无先验信息时也能使用，进而使得Bootstrap-Bayes法在小样本可靠性分析中具有更大的使用范围。然后，通过马尔科夫链蒙特卡洛（Markov Chain Monte Carlo, MCMC）方法中的Gibbs抽样简化后验分布的求解过程，避免了复杂的高维积分运算。最后，根据Arrhenius加速模型得出剩余电流动作断路器的可靠性预测结果，为用电人员提供有力的数据参考。

1 剩余电流动作断路器的加速退化试验

1.1 加速退化试验

作为一种高可靠性、长寿命产品，电子式剩余电流动作断路器进行寿命试验所需试验周期过长，因此，本文利用加速退化试验得到的退化数据对其可靠性进行评估。晶闸管、二极管、零序电流互感器等内部电子元器件的老化会造成电子式剩余电流动作断路器的失效。温度的升高将明显加快电子元器件的腐蚀老化过程，同时，印制电路板的绝缘物质在高温下将分解出有机气体，也会影响其他部分的性能。由此可见，温度是影响电子式剩余电流动作断路器性能退化的主要因素，高温将明显加快剩余电流动作断路器的性能退化过程[19]。因此，选取温度作为加速退化试验的加速应力。在保证剩余电流动作断路器的失效机理不变的情况下，为加快其退化速度，将试验温度应力水平分别设置为50℃、60℃、70℃、85℃。

参照GB/T 2689.1-1981《恒定应力寿命试验和加速寿命试验方法总则》中相关规定，综合考虑试验时间和试验成本，将每个温度应力水平下的试验样本数确定为5。因此，随机选取20只同批次生产的额定剩余动作电流值为30mA的电子式剩余电流动作断路器进行恒定应力加速退化试验。

在试验过程中，每24h测量一次剩余动作电流值，共测量28个周期。每个试验周期内先设置温度为25℃，并保持2h，在2h内将温度试验箱内的温度调至选定的温度应力水平并持续16h，最后在2h内将温度降低至25℃并保持2h。每个试验周期末尾时刻测量剩余电流动作断路器的剩余动作电流值。

试验平台主要由剩余电流动作断路器检测装置和温度试验箱组成。试验平台电路框图如图1所示。图中，L1为电源线，L2为零线，L3为检测线。

温度试验箱用于提供剩余电流动作断路器加速退化试验所需的高温环境。为了保证试验过程中剩余电流动作断路器能够可靠动作，利用剩余电流动作断路器检测装置通过导线L1、L2为其提供辅助电源。导线L1、L3是检测装置在检测剩余电流动作断路器的性能退化特征量时，向其提供剩余电流的通道，使其能够测定剩余电流动作断路器动作时对应的性能退化特征量。

1.2 退化数据分析

在50℃、60℃、70℃、85℃各组试验中，每个温度下的5个试品的剩余动作电流退化趋势相同，退化速率差异性不大。以60℃时剩余动作电流退化数据为例，对同一温度应力下5个剩余电流动作断路器试品的退化趋势进行分析，60℃时退化数据如图2所示。

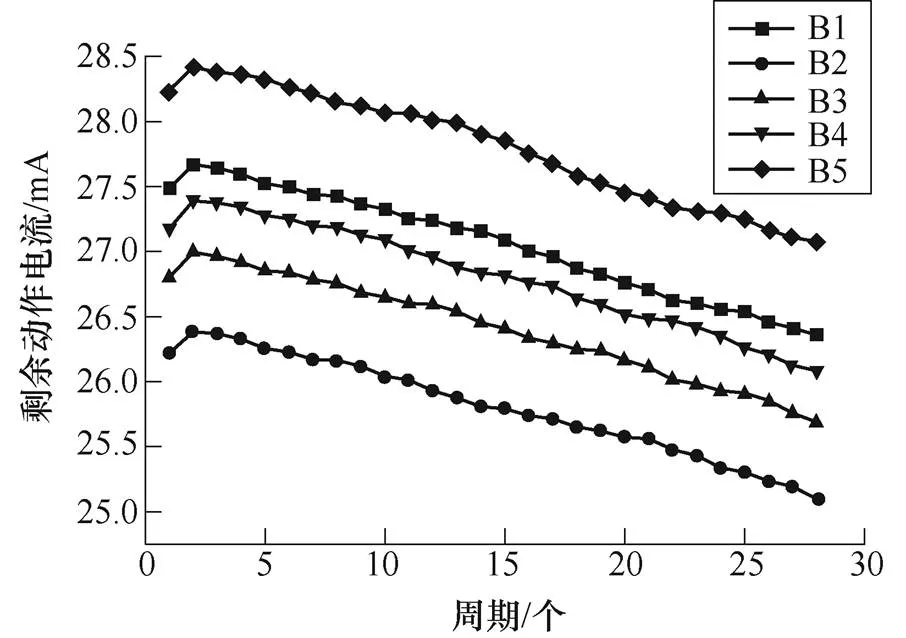
图2 60℃时剩余电流动作断路器的退化数据

由图2可知，随着试验时间的增加，剩余电流动作断路器的剩余动作电流值逐渐减小，呈下降趋势，且5个试品的剩余动作电流退化趋势基本一致，退化速率差异性很小。

比较不同温度时剩余动作电流值的退化趋势，每个温度应力下随机抽取1个试品，如图3所示。

由图3可知，各温度应力下剩余电流动作断路器的剩余动作电流值都呈现下降趋势，且下降速率随着温度的升高而增加。

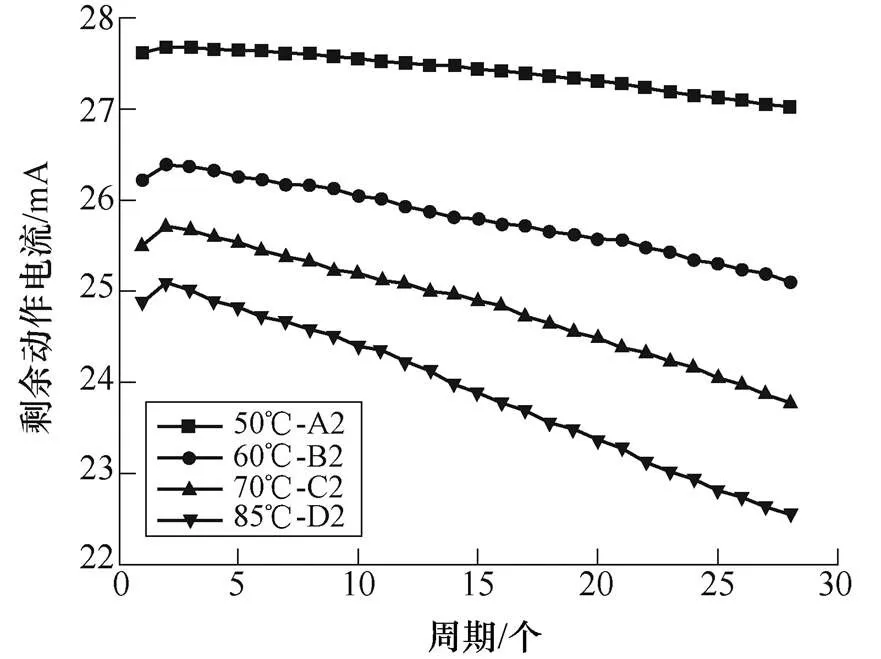
图3 不同温度剩余电流动作断路器的退化趋势

2 剩余电流动作断路器的伪失效寿命

2.1 外推伪失效寿命

对获得的退化数据进行退化轨迹拟合，利用最小二乘法估计不同温度下剩余电流动作断路器的性能退化轨迹参数，并根据失效阈值外推伪失效寿命值。试验所选剩余电流动作断路器的额定不动作电流值为15mA，假设试验初始时刻断路器的剩余动作电流值为，则相对失效阈值=-15。

以60℃下剩余电流动作断路器样品为例给出具体的伪失效寿命求解过程，利用最小二乘法将得到的剩余动作电流退化数据分别与常见的退化模型进行拟合，并根据残差二次方和最小原则确定最优拟合模型。常见的退化模型有线性函数（=+）、指数函数（=e）、对数函数（=ln+）和幂函数（= ）。60℃下断路器样品的拟合残差二次方和见表1。

表1 样本数据与各模型拟合的残差二次方和

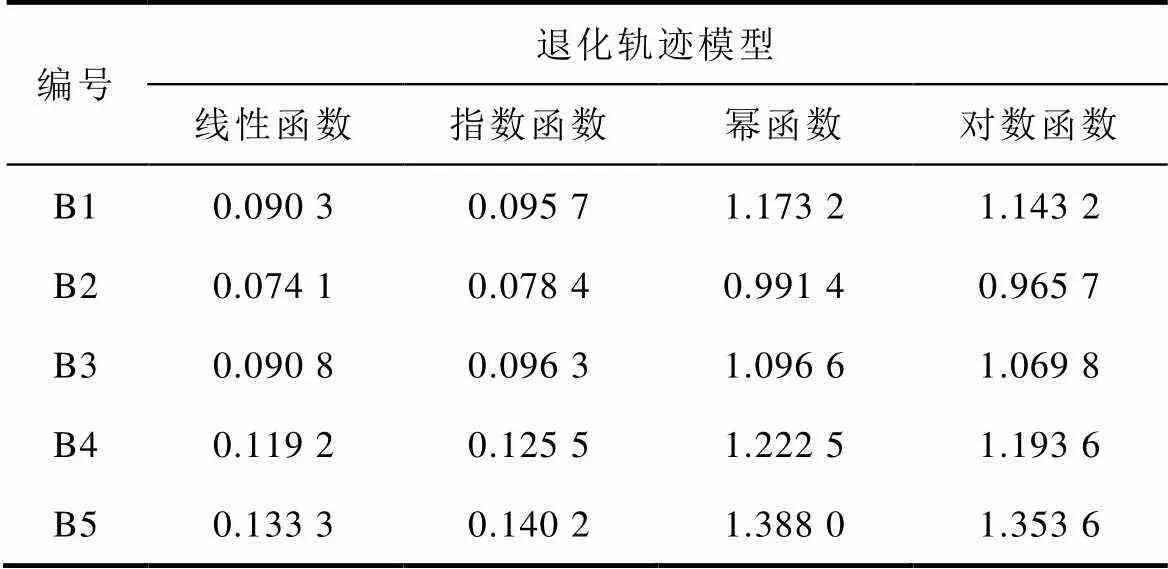
Tab.1 The residual sum of squares of the sample data and each model fitting

通过比较表1中各个退化模型下的残差二次方和，可以看出，5个样品在线性函数下的残差二次方和最小，残差二次方和越小说明拟合效果越好，即可以确定线性模型的拟合效果最好。

经验证，其余3个温度应力水平下，剩余电流动作断路器样本数据均与线性模型拟合的效果最好。由此得到4个温度应力下共20个剩余电流动作断路器线性退化模型的斜率和截距参数值以及外推得到的伪失效寿命值，见表2。

表2 伪失效寿命

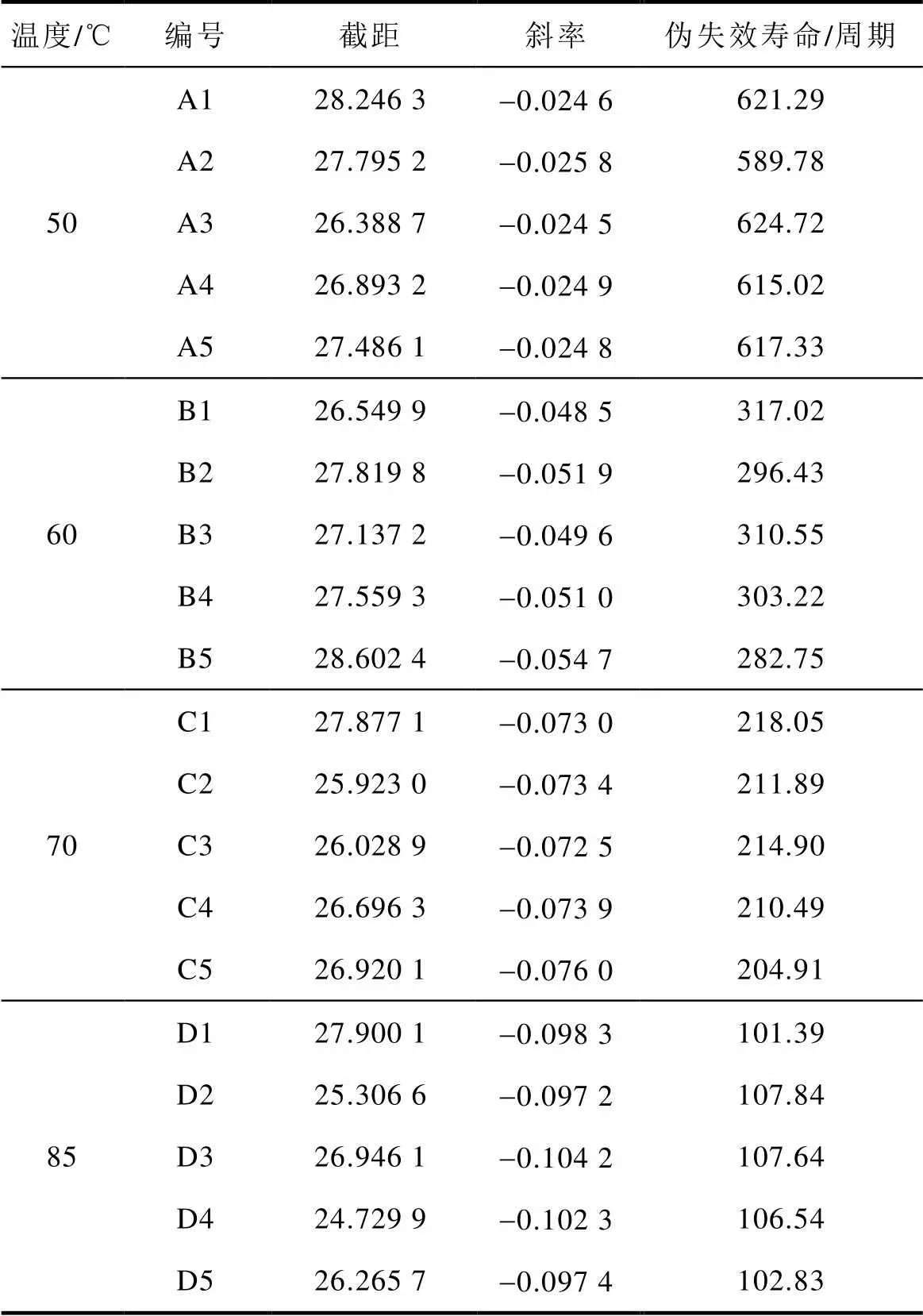
Tab.2 Pseudo-failure life

2.2 伪失效寿命分布类型检验

威布尔分布具有很好的兼容性，能够对各类数据进行拟合，可以描述出产品在不同时期的失效过程。因此，本文选择双参数威布尔分布对电子式剩余电流动作断路器进行可靠性建模。为了检验剩余电流动作断路器的伪失效寿命分布是否符合威布尔分布，利用K-S检验法对断路器的寿命分布进行检验，检验统计量见表3。

表3 检验统计量

Tab.3 Test statistics

当显著性水平为0.05时，通过临界值表可知K-S检验临界值为0.563 3，表3中各温度下伪失效寿命数据检验统计量均小于0.563 3，因此可认为剩余电流动作断路器的伪失效寿命服从威布尔分布。

3 剩余电流动作断路器的先验分布求解

3.1 先验信息的获取

灰色GM(1,1)模型是一种常用的小样本预测方法，预测过程简单、结果准确度高[20-22]。因此，本文利用灰色GM(1,1)模型对剩余电流动作断路器伪失效寿命数据扩充，将扩充后得到的伪失效寿命数据作为先验信息。以60℃时剩余电流动作断路器伪失效寿命的扩充为例，具体步骤如下：

（1）根据外推的剩余电流动作断路器伪失效寿命值，可以得到60℃的原始序列={282.75, 296.43, 303.22, 310.55, 317.02}，对其进行一次累加，得到累加生成序列为={282.75, 579.18, 882.40, 1 192.95, 1 509.97}。

（2）利用得到的累加生成序列建立白化微分方程为

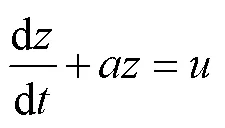
式中，、为待求解参数，其中为发展系数，为灰色作用量。

利用最小二乘法求,的解为

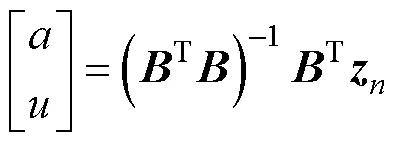
其中

在GM(1,1)模型中一般取值为0.5，求得=-0.022 5，=286.817 6。

（3）将得到的、值代入式（3）进行累减还原。

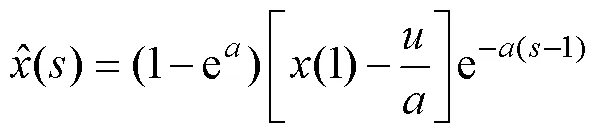
式中，为预测样本次序。得到10个扩充数据：{324.45,331.84, 339.40, 347.13, 355.03, 363.11, 371.38, 379.84, 388.49, 397.33}。

（4）利用式（4）计算样本的后验差，并根据表4模型精度检验对得到的灰色模型进行检验。后验差值越小，预测结果越精确。

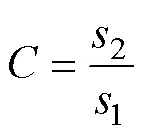
式中，1为原始数据的方均差；2为误差数据的方均差。

表4 模型精度检验

Tab.4 Model accuracy test

经计算后验差值为0.016 8，小于0.35，即所得灰色模型预测精度为优，预测结果较为精确。说明以灰色模型扩充后的数据作为剩余电流动作断路器的先验信息是可行的。

3.2 Bootstrap方法确定先验分布

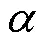
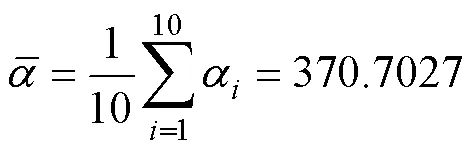
将得到的参数值代入威布尔分布的经验分布函数中，有

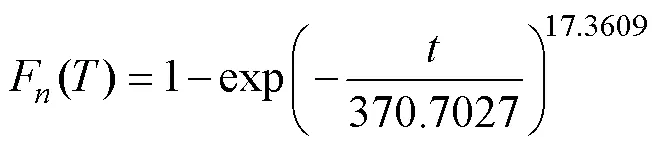
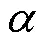
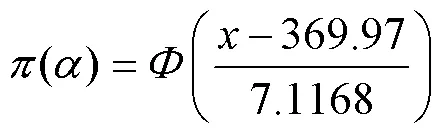
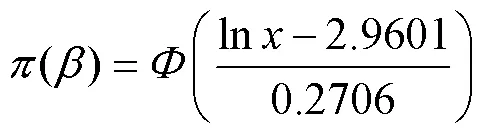
4 剩余电流动作断路器的后验分布求解

4.1 基于Gibbs的MCMC方法

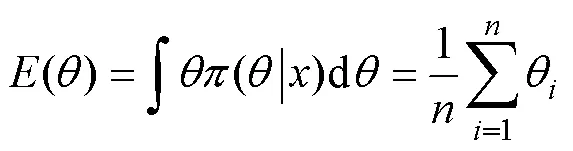
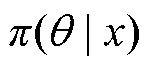
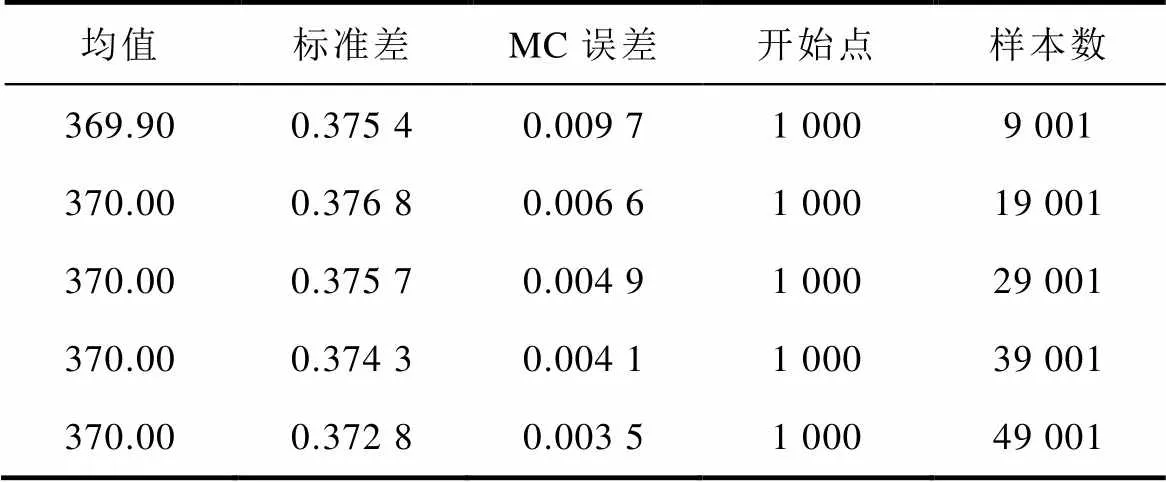
4.2 MCMC方法确定参数估计值

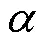
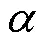
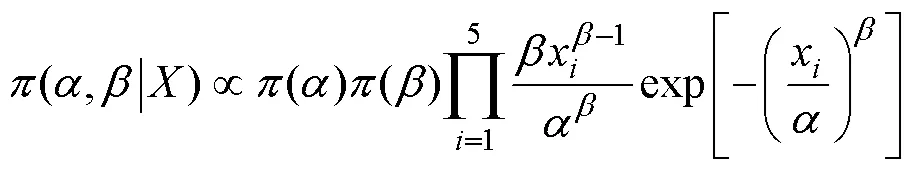
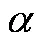
Tab.5 Posterior statistic of parameter

Tab.5 Posterior statistic of parameter

均值标准差MC误差开始点样本数 369.900.375 40.009 71 0009 001 370.000.376 80.006 61 00019 001 370.000.375 70.004 91 00029 001 370.000.374 30.004 11 00039 001 370.000.372 80.003 51 00049 001

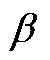
Tab.6 Posterior statistic of parameter

Tab.6 Posterior statistic of parameter

均值标准差MC误差开始样本样本数 6.682.4440.182 91 0009 001 6.692.4950.126 81 00019 001 6.702.4670.095 71 00029 001 6.682.4550.079 81 00039 001 6.682.4470.066 81 00049 001

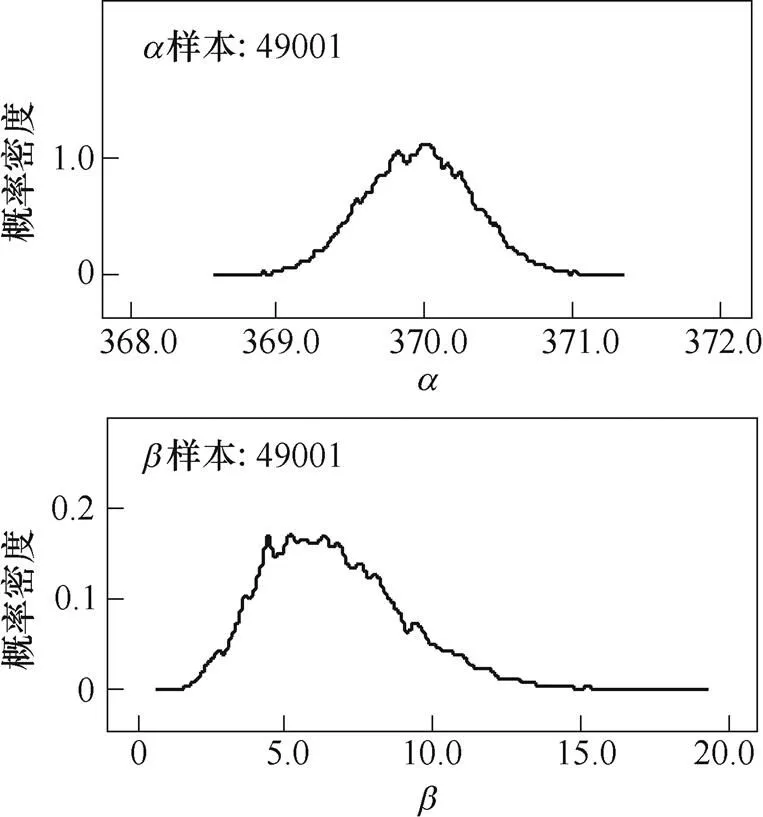
图4 参数和的后验概率密度

5 剩余电流动作断路器的可靠性评估

由于温度是影响剩余电流动作断路器性能退化的主要因素，故剩余电流动作断路器的退化速率和温度的关系可以用Arrhenius模型表示，即

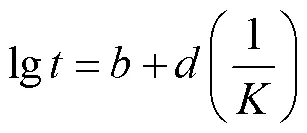
式中，为剩余电流动作断路器的特征寿命；为绝对温度；、为待求参数。

分别利用上述改进的Bootstrap-Bayes法对各组温度应力下剩余电流动作断路器威布尔分布参数进行求解。将各温度应力下剩余电流动作断路器参数后验统计量中的均值作为参数的估计值，用于评估正常使用环境下剩余电流动作断路器的可靠性。不同温度应力下剩余电流动作断路器的参数估计值见表7。

表7 剩余电流动作断路器的参数估计值

Tab.7 Parameter estimation value of leakage circuit breaker

图5中，数据点基本在一条直线上，拟合残差二次方和为0.001 7，相关系数为0.994 5，线性回归效果显著。未知参数、的估计值分别为-4.864 2和2 484.913 0，则剩余电流动作断路器尺度参数与温度的关系为

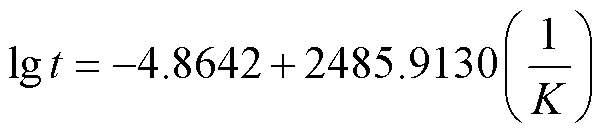
将剩余电流动作断路器正常使用环境温度（25℃）代入式（15），得到常温下尺度参数的点估计值为2 908.09。

正常使用环境下剩余电流动作断路器的可靠度函数为

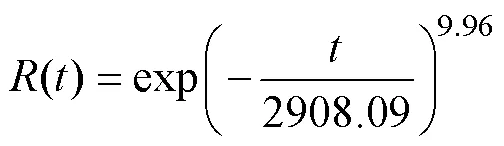
可靠度变化曲线如图6所示。

对于可靠性较高的产品，人们往往只关心高可靠度范围内产品的可靠性信息，所以本文重点只研究高可靠度范围内剩余电流动作断路器的可靠性评估。剩余电流动作断路器可靠度评估结果见表8。

由图6和表8可知，每个试验周期为24h，1 842个周期为1 842天，约为5年后剩余电流动作断路器的可靠度开始迅速下降；6.4年左右时，剩余电流动作断路器的可靠度约为0.90。根据得到的剩余电流动作断路器可靠度信息，使用人员应该在剩余电流动作断路器发生故障前及时更换剩余电流动作断路器，保证供电线路安全稳定运行。

表8 剩余电流动作断路器的可靠度评估

Tab.8 Reliability evaluation of leakage circuit breaker

6 结论

针对剩余电流动作断路器加速退化试验过程中没有失效数据的情况，充分利用剩余动作电流退化数据，采用改进Bootstrap-Bayes法对其可靠性进行评估。得到如下结论：

1）通过退化轨迹拟合外推剩余电流动作断路器的伪失效寿命，经检验其服从双参数威布尔分布。

2）利用GM(1,1)模型对剩余电流动作断路器伪失效寿命数据进行扩充得到的数据作为断路器的先验信息。

3）利用MCMC的Gibbs抽样结合Bayes公式得到参数的估计值，避免后验分布中的高维复杂积分计算，大大简化了后验分布的求解过程。

4）根据Arrhenius模型得到在正常使用环境温度下剩余电流动作断路器的伪失效寿命服从（2 908.09, 9.96）的威布尔分布，并得到剩余电流动作断路器的可靠性评估信息。

[1] 李奎, 王天朔, 王尧, 等. 基于数字恒流技术的B型剩余电流动作特性测试方法的研究[J]. 电测与仪表, 2020, 57(1): 147-152.

Li Kui, Wang Tianshuo, Wang Yao, et al. Research on test method of type B residual current operating characteristic based on digital constant current technology[J]. Electrical Measurement & Instru- mentation, 2020, 57(1): 147-152.

[2] 郑荣进, 丁柯婷, 黄晓生, 等. 剩余电流保护断路器动作特性自动测试系统设计[J]. 福建工程学院学报, 2018, 16(4): 381-385.

Zheng Rongjin, Ding Keting, Huang Xiaosheng, et al. An action characteristic automatic test system design of residual current protection circuit breaker[J]. Journal of Fujian University of Technology, 2018, 16(4): 381-385.

[3] 刘帼巾, 边鑫磊, 马晓燕, 等. 剩余电流动作断路器动作特性检测装置的研究[J]. 电测与仪表, 2018, 55(8): 113-118.

Liu Guojin, Bian Xinlei, Ma Xiaoyan, et al. Research on the detection device for the operating charac- teristics of leakage circuit breakers[J]. Electrical Measurement and Instrumentation, 2018, 55(8): 113- 118.

[4] 边鑫磊. 温湿度对电子式剩余电流动作断路器性能影响的研究[D]. 天津: 河北工业大学, 2017.

[5] 游颖敏, 王景芹, 舒亮, 等. 基于音频特征的交流接触器电寿命预测方法[J]. 电工技术学报, 2021, 36(9): 1986-1998.

You Yingmin, Wang Jingqin, Shu Liang, et al. The method of electrical life prediction considering the audio characteristics of AC contactor[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1986- 1998.

[6] 肖迁, 焦志鹏, 穆云飞, 等. 基于LightGBM的电动汽车行驶工况下电池剩余使用寿命预测[J]. 电工技术学报, 2021, 36(24): 5176-5185.

Xiao Qian, Jiao Zhipeng, Mu Yunfei, et al. LightGBM based remaining useful life prediction of electric vehicle lithium-ion battery under driving condi- tions[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5176-5185.

[7] 吴海洋, 缪巍巍, 郭波, 等. 基于遗传算法的BP神经网络蓄电池寿命预测研究[J]. 计算机与数字工程, 2019, 47(5): 1275-1278.

Wu Haiyang, Miao Weiwei, Guo Bo, et al. Research on battery life prediction of BP neural network based on genetic algorithm[J]. Computer & Digital Engin- eering, 2019, 47(5): 1275-1278.

[8] 李志刚, 刘伯颖, 李玲玲, 等. 基于小波包变换及RBF神经网络的继电器寿命预测[J]. 电工技术学报, 2015, 30(14): 233-240.

Li Zhigang, Liu Boying, Li Lingling, et al. Life prediction of relay based on wavelet packet transform and RBF neural network[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 233-240.

[9] 李奎, 高志成, 武一, 等. 基于统计回归和非线性Wiener过程的交流接触器剩余寿命预测[J]. 电工技术学报, 2019, 34(19): 4058-4070.

Li Kui, Gao Zhicheng, Wu Yi, et al. Remaining life prediction of AC contactors based on statistical regression and nonlinear Wiener process[J]. Transa- ctions of China Electrotechnical Society, 2019, 34(19): 4058-4070.

[10] Ibrahim M S, Fan Jiajie, Yung W K C, et al. Lumen degradation lifetime prediction for high-power white LEDs based on the Gamma process model[J]. IEEE Photonics Journal, 2019, 11(6): 1-16.

[11] 徐佳宁, 倪裕隆, 朱春波. 基于改进支持向量回归的锂电池剩余寿命预测[J]. 电工技术学报, 2021, 36(17): 3693-3704.

Xu Jianing, Ni Yulong, Zhu Chunbo. Remaining useful life prediction for lithium-ion batteries based on improved support vector regression[J]. Transa- ctions of China Electrotechnical Society, 2021, 36(17): 3693-3704.

[12] 范贤浩, 刘捷丰, 张镱议, 等. 融合频域介电谱及支持向量机的变压器油浸纸绝缘老化状态评估[J]. 电工技术学报, 2021, 36(10): 2161-2168.

Fan Xianhao, Liu Jiefeng, Zhang Yiyi, et al. Aging evaluation of transformer oil-immersed insulation combining frequency domain spectroscopy and support vector machine[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2161-2168.

[13] 王琪, 孙玉坤, 倪福银, 等. 一种混合动力电动汽车电池荷电状态预测的新方法[J]. 电工技术学报, 2016, 31(9): 189-196.

Wang Qi, Sun Yukun, Ni Fuyin, et al. A new method of battery state of charge prediction in the hybrid electric vehicle[J]. Transactions of China Electro- chnical Society, 2016, 31(9): 189-196.

[14] 王丰华, 曾全昊, 郑一鸣, 等. 基于Bayes估计相空间融合和CM-SVDD的有载分接开关机械故障诊断[J]. 中国电机工程学报, 2020, 40(1): 358-368, 402.

Wang Fenghua, Zeng Quanhao, Zheng Yiming, et al. A mechanical fault diagnosis of on- load tap- changers based on phase space fusion of Bayes estimation and CM-SVDD[J]. Proceedings of the CSEE, 2020, 40(1): 358-368, 402.

[15] Wu Min, Shi Yimin, Wang Yan. E-Bayesian estimation for competing risk model under pro- gressively hybrid censoring[J]. Journal of Systems Engineering and Electronics, 2016, 27(4): 936-944.

[16] 王新鹏, 张静远, 张洪刚. 无失效数据条件下装备贮存可靠性分析[J]. 系统工程与电子技术, 2019, 41(5): 1169-1172.

Wang Xinpeng, Zhang Jingyuan, Zhang Honggang. Reliability analysis for equipment in storage with zero-failure data[J]. Systems Engineering and Elec- tronics, 2019, 41(5): 1169-1172.

[17] 宋征宇, 方志耕, 赫武乐, 等. 基于贝叶斯理论的小子样运载火箭可靠性评估技术[J]. 深空探测学报(中英文), 2021, 8(1): 62-69.

Song Zhengyu, Fang Zhigeng, He Wule, et al. Research on reliability assessment methods of small sample based on Bayes theory[J]. Journal of Deep Space Exploration, 2021, 8(1): 62-69.

[18] 聂萌. 数控机床主轴可靠性分析[D]. 长春: 东北电力大学, 2019.

[19] Lakshminarayanan V, Sriraam N. The effect of temperature on the reliability of electronic com- ponents[C]//2014 IEEE International Conference on Electronics, Computing and Communication Tech- nologies, Bangalore, 2014: 1-6.

[20] Dejamkhooy A, Dastfan A, Ahmadyfard A. Modeling and forecasting nonstationary voltage fluctuation based on grey system theory[J]. IEEE Transactions on Power Delivery, 2017, 32(3): 1212-1219.

[21] 刘思捷, 张海鹏, 林舜江, 等. 夏季日最大降温负荷的估算和预测方法[J]. 电力系统保护与控制, 2016, 44(5): 75-81.

Liu Sijie, Zhang Haipeng, Lin Shunjiang, et al. An estimating and forecasting method for daily maximum cooling load in summer[J]. Power System Protection and Control, 2016, 44(5): 75-81.

[22] Zheng Zhen, Zha Bingting, Yuan Hailu, et al. Adaptive edge detection algorithm based on improved grey prediction model[J]. IEEE Access, 2020, 8: 102165-102176.

Reliability Evaluation of Electronic Residual Current Operated Circuit Breakers Based on Improved Bootstrap-Bayes

（State Key Laboratory of Reliability and Intelligence of Electrical Equipment Hebei University of Technology Tianjin 300130 China）

As a kind of high reliability and long-life product, the electronic residual current operated circuit breaker has few test data. In order to evaluate its reliability, a reliability evaluation method based on improved Bootstrap-Bayes was proposed. Firstly, with temperature as the accelerated stress, the accelerated degradation test for the residual current operated circuit breaker was carried out. The pseudo failure life was obtained by extrapolating the degradation data, and it was verified to obey the two-parameter Weibull distribution. Then, the GM(1, 1) model was used to expand the experimental data as the prior information, and the parameter estimates were obtained by Gibbs sampling in the Markov Chain Monte Carlo (MCMC) algorithm combined with Bayes formula. Finally, the Arrhenius acceleration model was used to evaluate the reliability of the residual current operated circuit breaker under normal use environment.

Electronic residual current operated circuit breaker, GM(1, 1) model, Bootstrap sampling, Bayes, Markov Chain Monte Carlo (MCMC), reliability evaluation

10.19595/j.cnki.1000-6753.tces.210229

TM506

河北省自然科学基金项目（E2020202221）和河北省高等学校科学技术研究项目（ZD2019041）资助。

2021-02-24

2021-04-21

刘帼巾 女，1972年生，教授，硕士生导师，研究方向为电器设备可靠性。E-mail: liuguojin72@163.com（通信作者）

王 泽 女，1996年生，硕士研究生，研究方向为电器可靠性及检测技术。E-mail: 1207258945@qq.com

（编辑 崔文静）