基于改进型降阶观测器的永磁直驱伺服电动机转矩扰动抑制策略

卜飞飞 郭子韬 顾毅君 轩富强 秦海鸿

基于改进型降阶观测器的永磁直驱伺服电动机转矩扰动抑制策略

卜飞飞1郭子韬1顾毅君2轩富强1秦海鸿1

（1. 南京航空航天大学自动化学院 南京 211106 2. 中国船舶重工集团公司第七二四研究所 南京 211106）

由于永磁直驱电机的直驱特性，电机转速平稳性受转矩扰动影响大，低速运行时受齿槽转矩影响，电机转速波动剧烈。该文分析传统比例积分速度控制方法无法兼顾跟踪性能和抗扰性能的缺点。为此引入传统降阶状态观测器，对转矩扰动进行估计和前馈补偿；分析系统扰动转矩到真实转矩之间传递函数的伯德图及锯齿波响应，根据零极点对消原则对传递函数进行期望设计，引入微分环节对传统降阶观测器进行改进，给出改进观测器的锯齿波响应并证明其补偿响应速度的提升，提出基于引入微分模块的降阶观测器前馈补偿方法。搭建永磁直驱伺服电动机扰动抑制实验平台，通过仿真和实验验证改进的降阶观测器对补偿谐振的抑制具有良好性能，且抗扰动能力更强，实现较大扰动低速下的稳定运行。

降阶观测器 永磁伺服电动机 直接驱动 转矩扰动抑制

0 引言

永磁同步电机（Permanent Magnet Synchronous Motor, PMSM）具有功率密度大、功率因数高、起动转矩大、过载能力强、响应快、效率高等优点，在伺服驱动等众多领域得到了广泛应用[1-2]。传统伺服系统中的执行机构包含大量如齿轮、皮带等传动机构，这些机构的存在，使得伺服系统效率降低，中间传动环节的弹性形变，传动机构间隙会造成伺服系统控制精度下降[3-4]。为解决上述问题，直接驱动技术应运而生，通过将负载和电机轴直接相连，取消伺服系统中的传动机构，避免了减速机弹性形变、传动误差和组件摩擦的影响，使伺服系统能够拥有更高的定位精度、效率和响应能力，降低了振动噪声和维护成本[5]。但由于直驱伺服电动机轴和负载直接相连，外部扰动直接传递到电机本身导致电机对扰动更加敏感，使伺服系统精度和性能降低[5]。电机本身的齿槽转矩、高次电流谐波、磁阻效应等造成的输出扰动会直接作用在负载上，影响系统性能[6]。在低速工况下，齿槽转矩、摩擦转矩等扰动会表现出更低的频率，由于电机本身具有低通滤波器特性[7]，对低频扰动抑制能力差，所以上述问题带来的影响更加明显[8]。

国内外众多学者通过改进控制算法，对电机扰动进行抑制，典型的有滑模控制、比例谐振控制、重复控制、迭代学习控制、自适应控制、自抗扰控制、鲁棒控制、观测器法等。文献[8]提出了一种改进型的滑模控制策略，但由于滑模控制本身存在抖振现象，电机无法避免的会有抖动[9]。自适应控制通常是自调整系统的控制器参数，文献[10]设计了一种模型参考自适应速度控制器，通过自调整补偿项参数对不确定扰动进行补偿，但是模型的高阶项增加了计算负担。重复控制针对周期性扰动有较好的抑制效果，但用在速度环中可能会因为电流环延时和速度测量延时使高频的相位裕度小于零，进而带来不稳定的风险[11]。文献[12]提出通过闭环迭代学习补偿系统的非线性，但迭代学习控制在抑制非周期性扰动时可能反而会有放大扰动的效果[13]。且文献[12]是基于对象模型和扰动模型已知条件下设计，而在实际应用中扰动频率经常发生变化，无法提前预知所有的扰动信息。鲁棒控制的常用方法之一是∞控制[14]，但是该方法往往对计算能力要求较高，需要较大的运算资源，甚至一些方案还停留在仿真阶段，在工程中应用有一定困难。采用观测器对扰动转矩进行前馈补偿，对周期性扰动和非周期性扰动均有一定的抑制效果，能够实时观测实际运行中电机受到的时变且难以预测的扰动，无需提前预知扰动信息，而且实现简单，对计算资源需求不高，在工程中也更加适用。

文献[15]通过全阶观测器观测出位置、转速和转矩，并对估计转矩进行前馈。但对于永磁电机的速度控制来说，往往不需要观测所有的状态变量，可通过降阶[16]对全阶观测器进行简化，只观测转速和转矩，而且抗干扰能力并未减弱，可调整参数减少，易于实现。但传统降阶观测器对扰动的观测存在滞后[17]，对突变的扰动跟随效果较差，在对周期性扰动进行补偿时会出现周期性的抖动（这种出现周期性抖动的现象后文称：补偿谐振）。为此，本文对传统降阶观测器进行改进，以实现低速运行时补偿谐振的抑制。

本文首先分析了基于传统PI调节器的矢量控制策略，说明了其扰动抑制性能和跟随性能之间存在的矛盾，然后推导了传统降阶观测器模型，并分析了传统降阶观测器进行扰动补偿时出现低速补偿谐振现象的机理。在此基础上提出了一种改进型的降阶观测器，通过引入微分环节来提高观测器的补偿响应速度，再将其观测值前馈至电流环输入实现对扰动转矩的补偿，并理论分析了改进型降阶观测器抑制补偿谐振的原理，最后通过仿真和实验验证了所提策略的有效性。

1 基于传统PI调节器的矢量控制缺点

永磁同步电机在dq坐标系下的模型为

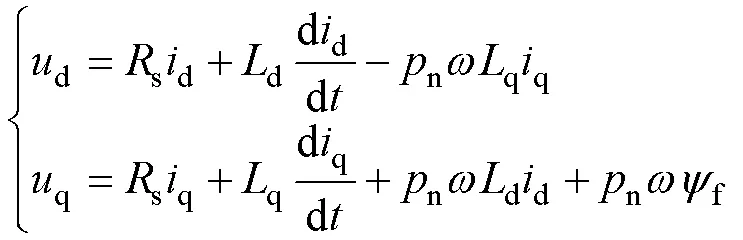
式中，d、q分别为d、q轴电压；d、q分别为d、q轴电流；s为定子绕组每相电阻；d、q分别为d、q轴电感；n为极对数；f为永磁体磁链；为转子角速度。

机械运动方程为

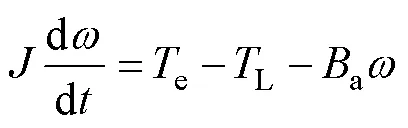
式中，为转动惯量；a为阻力系数；e为电磁转矩；L为负载转矩。

本文中采用d0的控制方法，其控制结构如图1所示。由于速度环变化速度远小于电流环的调节速度，在分析速度环路时将电流环等效为一阶纯惯性环节。图2给出了典型的速度环结构。

图1 永磁同步电机id=0矢量控制结构框图

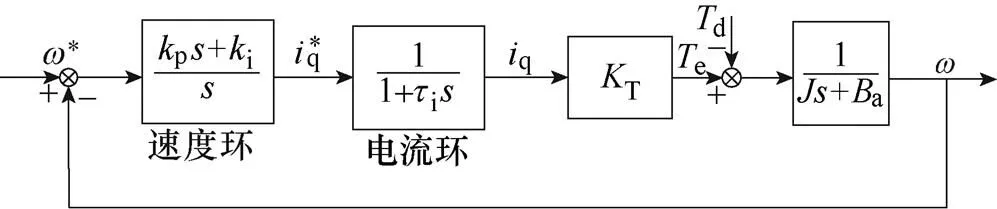
图2 速度环结构

为分析跟随特性，将电流环的传递函数等效为“1”，可以得到速度环的闭环传递函数为

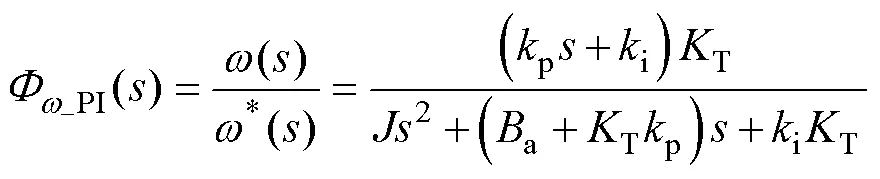
式中，d为扰动转矩；PI()为灵敏度函数，是扰动经控制对象输出后与实际转速之间的传递函数[18-19]，用来分析传统控制策略下转矩扰动与由其产生的速度波动之间的增益关系。

图3描述了跟随性和抗干扰性之间的矛盾，a、b、c、d代表i/p的不同取值（i/p满足d＞c＞b＞a/＞a），可以看出，当i/p逐渐增大时，闭环零极点的移动导致速度的阶跃响应从无超调变为有超调最后变为振荡，且振荡幅度呈增加趋势，跟随性能逐渐降低。但是，图3b中转矩扰动抑制性能的表现较图3a则是相反的，即i/p的逐渐增加会提高干扰抑制的程度和快速性。由以上分析可得出结论，经典的PI控制存在局限：不能同时满足抗干扰能力和速度跟踪能力，只能折中选取。

图3 PI控制策略下跟随性和抗扰性之间的矛盾

2 基于传统观测器的转矩扰动补偿谐振现象及机理分析

将扰动视为状态变量进行观测的观测器可称为扰动观测器，降阶状态观测器（Reduced order State Observer, RSO）是其典型的一种，它低速性能好[17, 20]，且易于实现，适合本文的研究对象。

2.1 降阶观测器设计

在电机控制系统中，观测变量为转速和转矩，位置信号由传感器实际测量得到。

其中

在式（5）基础上引出观测器，其表达式为

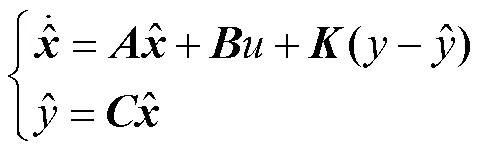
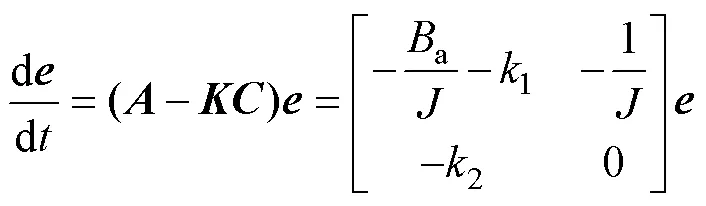
式（7）特征方程为

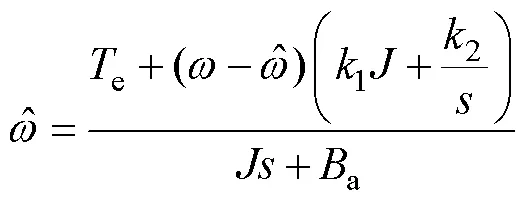
（10）

式中，c为补偿电流值。系统控制策略框图如图4所示。

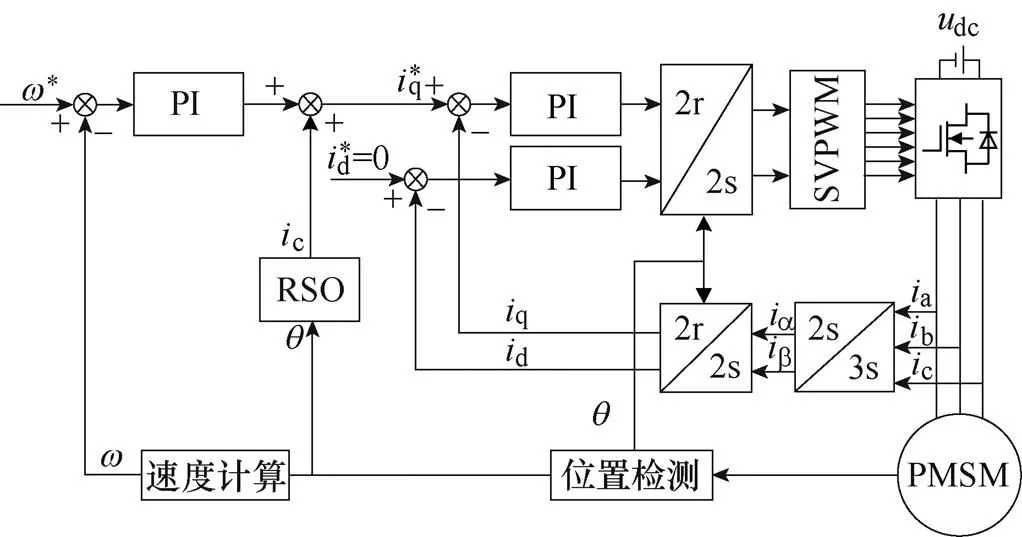
图4 PI-RSO控制策略框图

2.2 传统观测器补偿出现的补偿谐振现象分析

2.2.1 PI-RSO仿真结果

为了验证PI-RSO控制策略性能，本文依据样机的相关参数（见表1），建立了永磁直驱伺服电动机及其驱动系统的仿真模型。该样机有较大的齿槽转矩，这是因航天设备对于空间占用和质量的设计要求，在电机结构设计时，取消了安装于电机末端的电磁制动器，并在电机结构设计时，通过增加齿槽转矩幅值来实现定位制动。

表1 三相永磁直驱伺服电动机模型主要参数

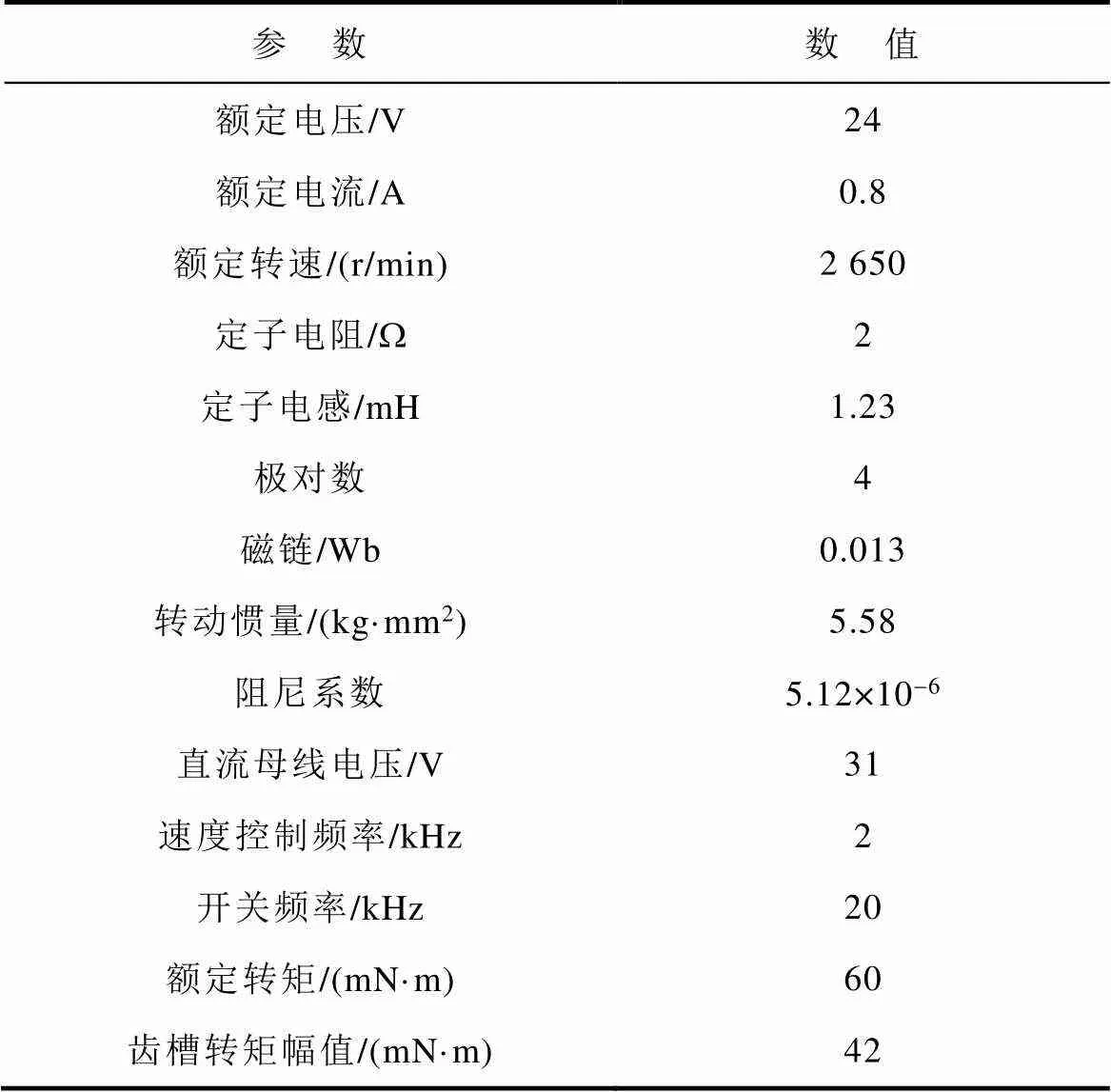
Tab.1 Main parameters of three phase permanent magnet direct drive servo motor model

为了同时验证该算法对周期性和非周期性扰动的抑制能力，在10s时突加额定转矩。电机运行于1r/min的给定转速，可得转速、电流和转矩的仿真波形，如图5所示。

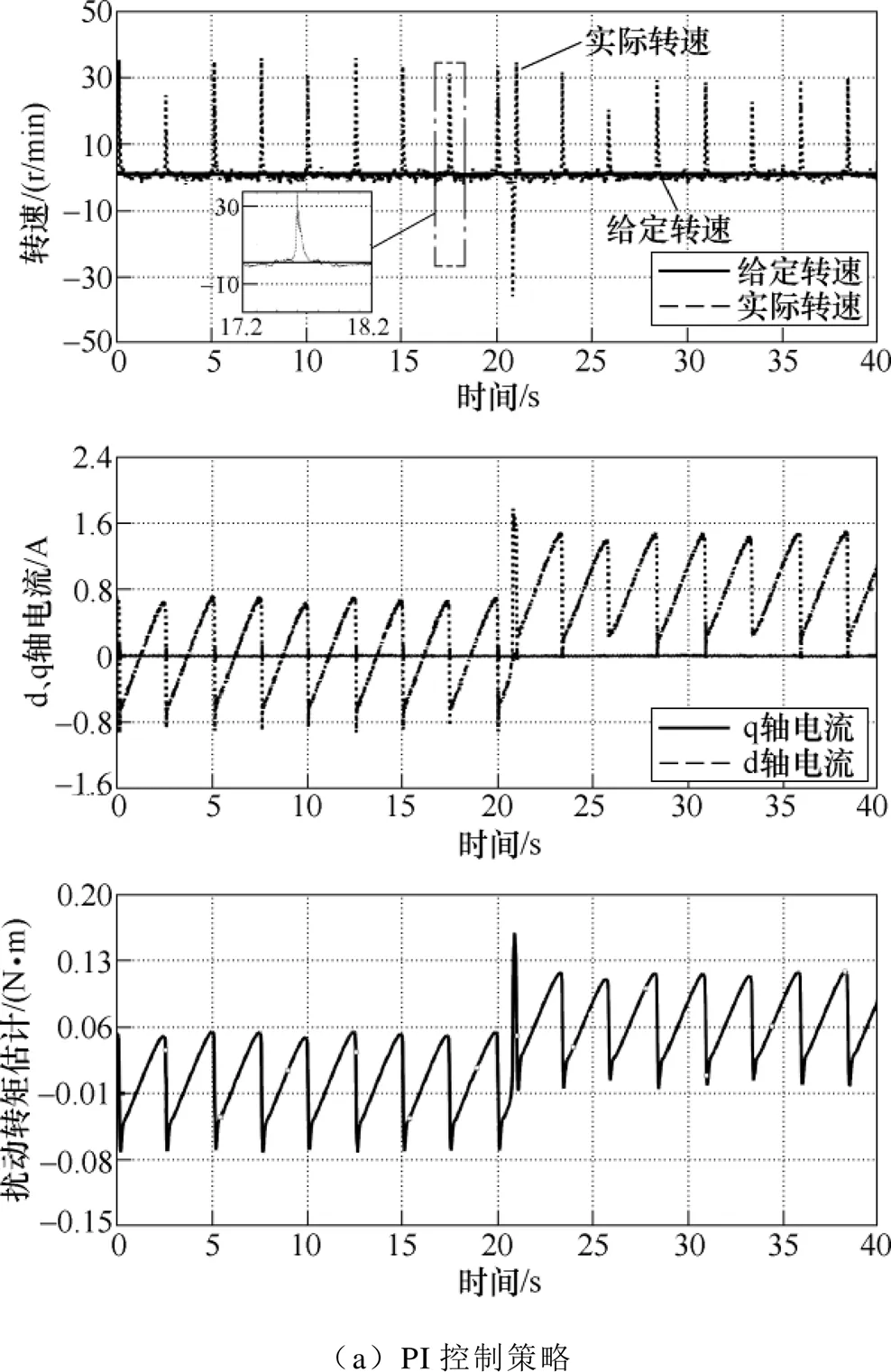
由图5可以看出，传统PI控制策略下，电机转速波动很大，稳态波动峰值达到将近28r/min，在突加负载时，转速跌落将近34r/min。在PI-RSO控制策略下，虽然突加负载时转速跌落降低，约21r/min，但出现了周期性正反转（称为谐振点），稳态时速度波动峰值也很大，约29r/min。可以看到，PI- RSO的策略的q轴电流波形在峰值之后的跌落处出现了振荡，并且扰动转矩估计值紧紧跟随实际值，但均成锯齿状。

由上述现象可知，PI-RSO策略虽然能在一定程度上抑制非周期性转矩扰动，但是对于本文转矩扰动，补偿时反而产生了转子谐振，即转速周期性的在某些时间点出现正负振荡，即补偿谐振。

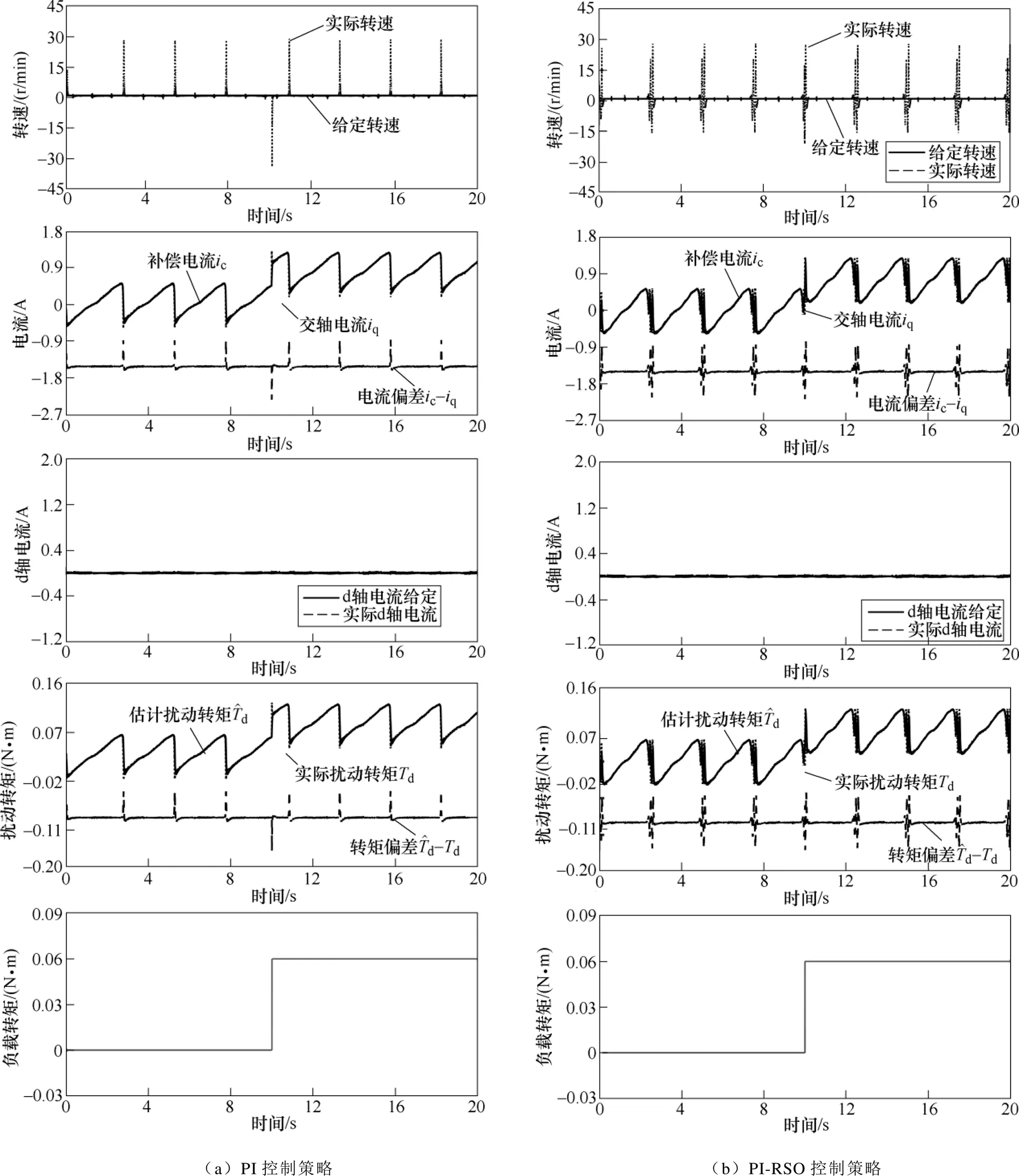
图5 PI控制策略和PI-RSO控制策略在1r/min给定速度下的仿真结果

2.2.2 补偿谐振机理分析

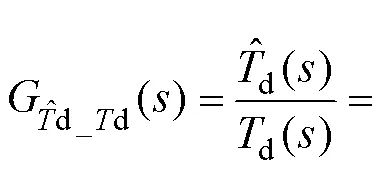
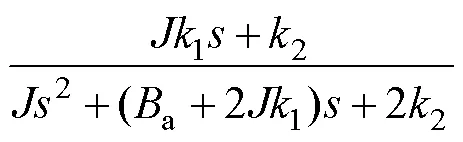
其中

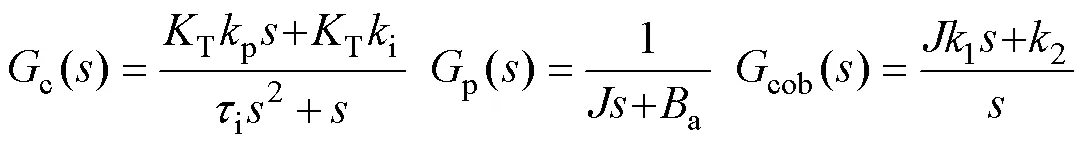
由式（11）可知，传递函数的两个极点G1、G2和一个零点G分别为

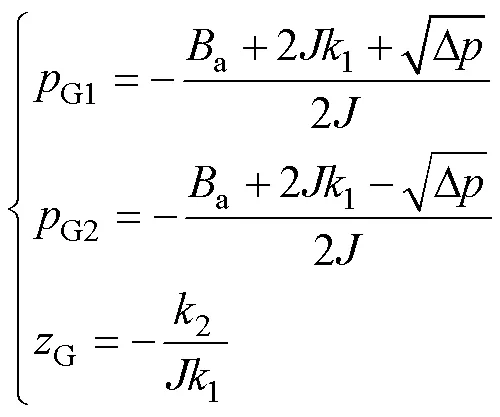
其中

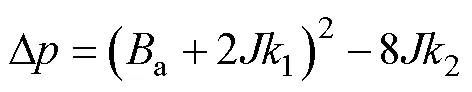
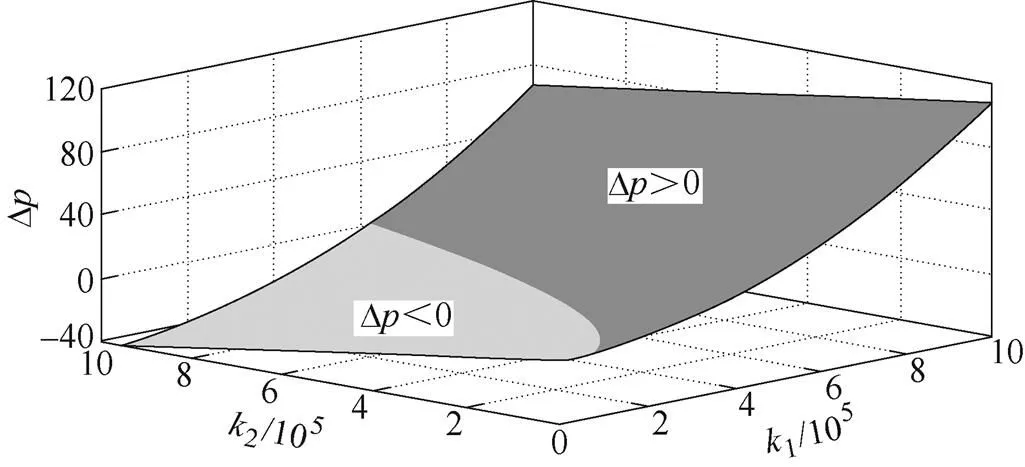
图6 与k1和k2关系的三维图像

假设2为定值，逐渐增加1，不同观测器参数下传统RSO的Bode图及其对应的锯齿波响应如图7所示。由图7可知，极点G1和G2逐渐由复极点变为实极点，且由式（12）可知，极点逐渐向左移动，同时零点向右移动。相应地，锯齿波响应如图7b所示，随着1逐渐增大，振荡消除，但是由于极点分布对锯齿波信号阶跃点跟踪存在一定调节时间，而且从图7a Bode图的相位可知，在各个频率点处相位滞后是不可避免的。

图7 不同观测器参数下传统RSO的Bode图及其对应的锯齿波响应

扰动观测器闭环时转矩方程为

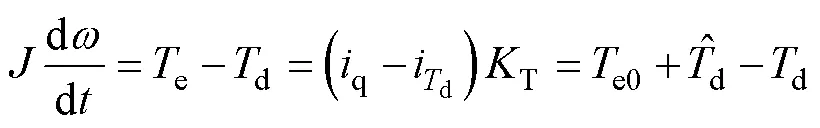
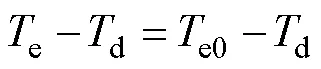
从图5中可以看出，当电机爬行时，扰动转矩大致呈锯齿波，而电机的突然加载，则会进一步造成扰动转矩呈现阶跃式变化。

由上述理论分析，扰动观测器对于锯齿波和阶跃信号的跟踪存在下降或上升时间，所以当实际扰动转矩因为爬行原因在扰动转矩呈阶跃式上升到峰值或下降到最小值时，估计转矩的跟踪需要一定的调节时间，而且也存在相位的延迟，这就造成了补偿滞后。该滞后造成扰动转矩的估计偏差出现尖峰，而且因为是周期性的转矩脉动，尖峰的出现也呈周期性。反映到电流上，当补偿电流给到q轴给定端后，扰动转矩对应的电流和q之间的偏差也存在周期性的尖峰，从式（13）的右端可知，这会导致转

速出现大的正加速度，进而出现图5所示的很高的转速峰值。随后实际扰动转矩会再次上升，与估计转矩相交，使估计偏差由正变负，进而造成负的加速度，电机减速甚至变成反转，随后转矩估计偏差和电流偏差出现振荡，加速度也因此呈现振荡状态，进而导致转速出现振荡，如图5的转速波形所示，即形成补偿谐振。

3 基于PI-DRSO的转矩扰动抑制策略

3.1 抑制传统观测器补偿谐振方法分析

从式（11）可知，传统观测器补偿策略下，系统观测转矩与实际扰动转矩的传递函数中，存在一个零点和两个极点，由于这种零极点个数的不对等，导致观测器参数无论如何选取，系统都有无法消除的相位滞后，这种滞后进一步导致了补偿谐振的出现。为了消除传统观测器的补偿谐振现象，考虑从零极点对消角度出发，通过改进观测器结构，使观测转矩与实际扰动转矩的传递函数的零极点对消，从而消除观测器中固有的滞后。假设改进后观测器观测转矩到真实转矩的传递函数为

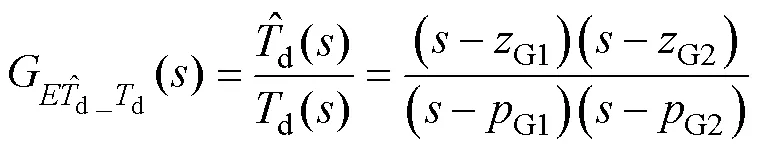
式中，G1、G1、G1、G2分别为两个极点和两个零点。因为a相对较小，在这里对其忽略，若此时G1、G2、G1、G2实现对消，可以得出改进后传递函数为

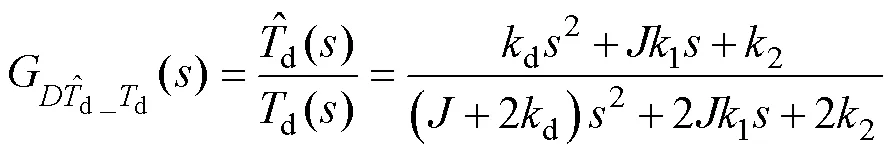
可以画出此时观测器对应的零极点和锯齿波响应如图8所示。

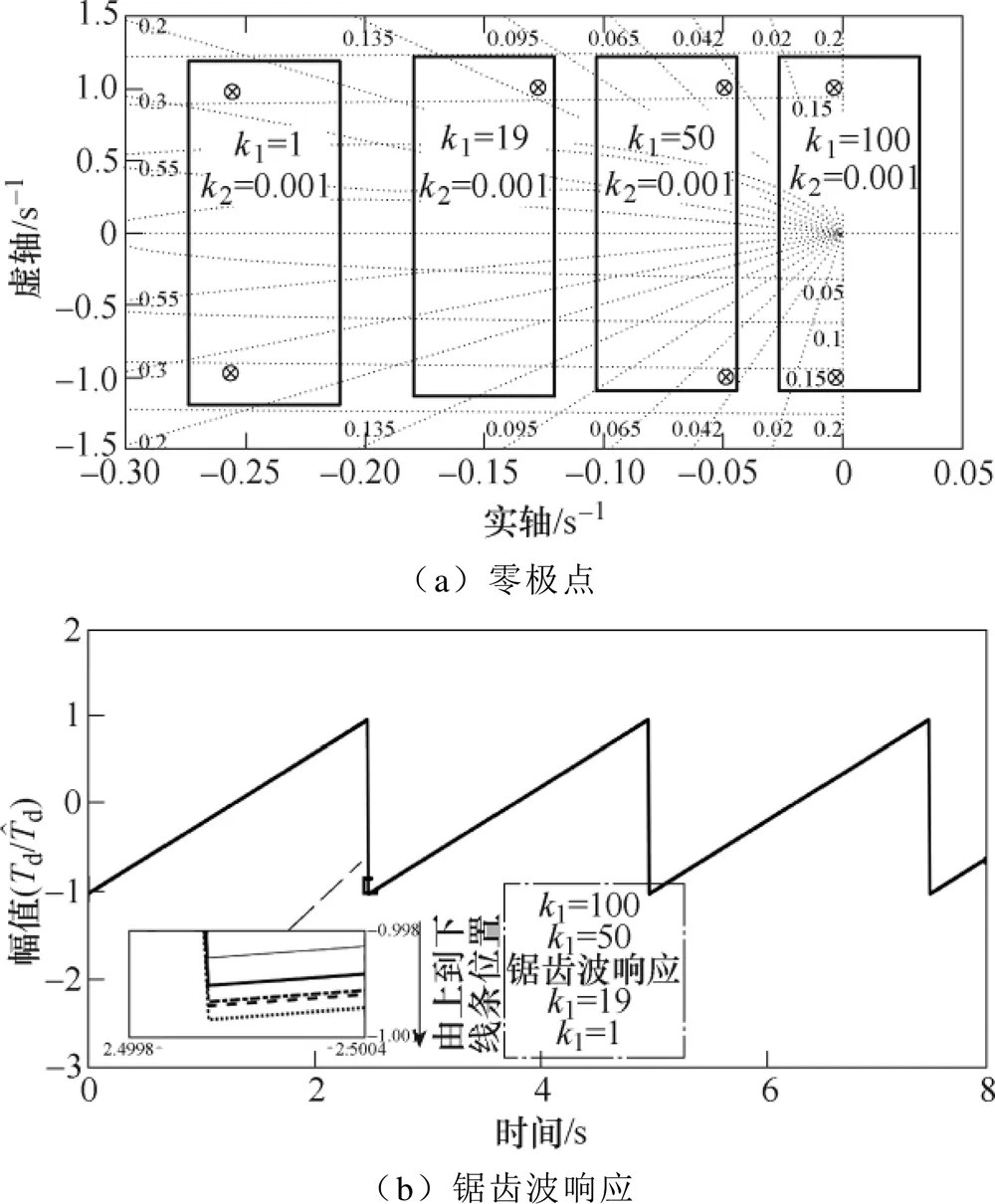
图8 kd=0.005时不同观测器参数k1下DRSO的零极点图及其对应的锯齿波响应

由式（15）可知，传递函数的两个极点GD1、GD2和两个零点GD1、GD2分别为

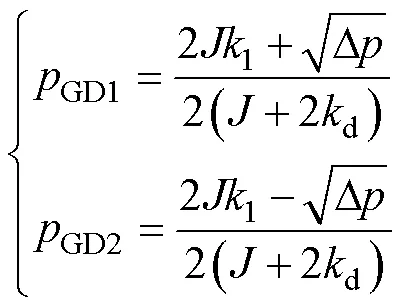
其中

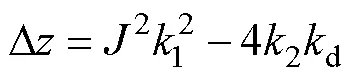
3.2 PI-DRSO策略

将式（15）进行化简可得改进后观测器结构为

从式（20）可得，仅需引入一个微分环节即可实现对扰动转矩的无滞后观测，所以这里提出一种引入微分模块的降阶状态观测器（Differential Reduced order State Observer, DRSO）。其控制框图如图9所示。将该观测器引入PI策略中进行前馈补偿（补偿方法与图4相同），即构成PI-DRSO策略。

4 仿真及实验验证

4.1 仿真证明

仿真时的电机参数见表1，图10给出了PI-DRSO策略在1r/min给定下的仿真结果。

图10 PI-DRSO策略在1r/min给定下的仿真结果

观测器参数取值为：1=50，2=0.002，d=0.005，和图5中PI-RSO策略结果与PI-DRSO策略仿真结果对比可以看出，在1r/min的速度给定下，PI-RSO策略和PI-DRSO策略的速度稳态峰值分别为29r/min和7r/min，加载时的速度跌落分别为21r/min和17r/min。而且，PI-DRSO策略不会周期性地出现速度正负振荡。该结果表明，PI-DRSO策略能够很好地解决传统PI-RSO策略在低速时遇到的补偿谐振问题，具有更好的抗转矩扰动性能。

4.2 实验验证

实验使用“DSP+FPGA”永磁电机伺服驱动平台如图11所示，该实验平台主要包括主功率电路、控制电路、永磁直驱伺服电动机三部分，其中主功率电路和控制电路由四层板构成，分别是顶层核心板，实现对整个电机驱动系统的控制；通信和接口板，将控制信号和采样信号进行转接并实现驱动器和电脑间的通信；旋变解码和采样板，实现电机各个信号的采集；电源和驱动板，驱动电机并为前述各层板提供电源。DSP芯片采用TI公司的TMS320C6701，FPGA芯片采用Altera公司的EP4CE22F17I7，实验所用电机参数见表1。

图11 实验平台整体硬件实物

4.2.1 PI-DRSO策略不同参数下的实验结果

改进策略所引入微分模块的关键参数为d，为了在实际运行工况中对该值进行确定，下面给出d= 0.001、0.005、0.01下的实验结果，如图12所示。实验中转速控制周期设定为5ms，电流环控制周期设定为0.5ms。

从图12可以看出，在转速给定为1r/min的工况下，d=0.001、d=0.005、d=0.010时的稳态速度峰值分别为29r/min（电机反转时为-29r/min）、15r/min和13r/min，且估计转矩的噪声逐渐增大。d=0.001时，速度在一些时间点仍然存在振荡现象，即补偿谐振；d=0.005、d=0.01时，补偿谐振现象消除。实验结果表明，在传统RSO中引入微分模块的PI-DRSO策略可以抑制转子谐振现象，而且随着d值的增加，转子谐振的抑制效果会逐渐增加，直到完全消除。同时，转矩扰动的抑制能力随d的增加而逐渐提高。但是，因为噪声量的限制，d不能无限升高，所以对于本文的研究对象电机来说，取d=0.005适宜。

4.2.2 PI策略、PI-RSO策略和PI-DRSO策略的对比实验结果

为进一步验证所提出PI-DRSO控制策略的有效性，取d=0.005，与PI和PI-RSO控制策略在实验平台上进行对比实验，并在运行中突加额定负载，结果如图13所示。

从图13a中可以看出，PI策略在稳态时周期性地出现严重的低速爬行和卡顿现象，频率为0.4Hz，与扰动转矩的频率相同，且速度峰值为33r/min；突加载时速度跌落达到35r/min。q轴电流与扰动转矩一样近似成锯齿波，而且锯齿波的阶跃式下降点与速度峰值出现的时间点相同。加载时，q轴电流和扰动转矩都出现了过冲。图13b PI-RSO策略的稳态速度峰值为32r/min（反转时为-32r/min），且会周期性地出现转速正负振荡（补偿谐振）。而图13c的PI-DRSO控制策略不会出现速度正负振荡，虽然也存在低速爬行现象，但稳态和动态时的速度波动明显降低（16r/min，17r/min）。q轴电流和估计扰动转矩在加载时过冲相比PI策略低，但扰动转矩的观测噪声有所增加。

实验结果表明，PI-RSO控制策略在低速运行工况下存在补偿谐振现象，即周期性的出现速度正负振荡。而PI-DRSO控制策略能对补偿谐振产生抑制作用，并且具有良好的转矩扰动抑制能力。

5 结论

本文首先对传统PI策略在跟踪性能和抗扰性能之间的矛盾进行了分析，就其不足之处，引入降阶观测器对扰动转矩进行观测，并将其转化为电流前馈补偿到交轴电流给定端，从而对转矩扰动进行抑制。但是传统的降阶观测器在电机低速爬行状态下可能因为补偿滞后造成转子周期性地出现谐振，文中分析了该谐振现象出现的机理，并由此提出了一种引入微分模块的无补偿滞后PI-DRSO控制策略，从而解决了补偿谐振问题，更好地实现了转矩扰动抑制。通过仿真和实验分析可得出以下结论：

1）将微分环节引入降阶观测器中，能够提高观测器的补偿响应速度。改进的观测器对扰动转矩的观测无理论滞后，有效地解决了传统观测器中的补偿谐振问题。

2）基于降阶观测器的扰动抑制方法较其他方法相比，无需提前预知扰动信息，适合应对在实际应用中可能出现的各种无法预测的扰动转矩，在低速下观测性能较好，且实现简单，无需改变传统PI控制结构，可调参数较少，易于工程实现。

3）改进的降阶观测器虽然加入了微分环节，但其微分系数可调，不会使电机在低速工况下的位置信号测量误差被放大。

4）本文所提的基于改进型降阶观测器补偿的扰动抑制方法，可以与不同的控制算法相结合，形成复合控制算法，普适性较强。本文是在传统PI控制的基础上进行了补偿，但PI控制存在其局限性，若将其他控制方法与观测器进行结合可能会带来更好的扰动抑制效果，后续将开展这方面研究。另外，对于不同的扰动类型，改进的观测器效果及谐振点出现的规律，本文也将进行进一步深入研究。

[1] 梁戈, 黄守道, 李梦迪, 等. 基于高阶快速终端滑模扰动观测器的永磁同步电机机械参数辨识[J]. 电工技术学报, 2020, 35(增刊2): 395-403.

Liang Ge, Huang Shoudao, Li Mengdi, et al. A high-order fast terminal sliding-mode disturbance observer based on mechanical parameter identi- fication for PMSM[J]. Transactions of China Elec- trotechnical Society, 2020, 35(S2): 395-403.

[2] 尹忠刚, 靳海旭, 张彦平, 等. 基于扰动观测器的交流伺服系统低速爬行滤波反步控制方法[J]. 电工技术学报, 2020, 35(增刊1): 203-211.

Yin Zhonggang, Jin Haixu, Zhang Yanping, et al. Disturbance observer-based filter backstepping control with low speed crawling for AC servo system[J]. Transactions of China Electrotechnical Society, 2020, 35(S1): 203-211.

[3] 鲍晓华, 刘佶炜, 孙跃, 等. 低速大转矩永磁直驱电机研究综述与展望[J]. 电工技术学报, 2019, 34(6): 1148-1160.

Bao Xiaohua, Liu Jiwei, Sun Yue, et al. Review and prospect of low-speed high-torque permanent magnet machines[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1148-1160.

[4] Bu Feifei, Yang Zhida, Gao Yu, et al. Speed ripple reduction of direct-drive PMSM servo system at low-speed operation using virtual cogging torque control method[J]. IEEE Transactions on Industrial Electronics, 2021, 68(1): 160-174.

[5] Liu Chengcheng, Wang Kelin, Wang Shaopeng, et al. Torque ripple reduction of synchronous reluctance machine by using asymmetrical barriers and hybrid magnetic core[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(1): 13-20.

[6] Niu Shuangxia, Ho S L, Fu Weinong. A novel direct- drive dual-structure permanent magnet machine[J]. IEEE Transactions on Magnetics, 2010, 46(6): 2036- 2039.

[7] Xia Changliang, Ji Bingnan, Yan Yan. Smooth speed control for low-speed high-torque permanent-magnet synchronous motor using proportional integral resonant controller[J]. IEEE Transactions on Industrial Elec- tronics, 2015, 62(4): 2123-2134.

[8] Bu Feiei, Xuan Fuqiang, Yang Zhida, et al. Rotor position tracking control for low speed operation of direct-drive PMSM servo system[J]. IEEE/ASME Transactions on Mechatronics, 2021, 26(2): 1129- 1139.

[9] Zhang Bitao, Pi Youguo. Enhanced sliding-mode control for permanent magnet synchronous motor servo drive[C]//Chinese Control and Decision Con- ference, Taiyuan, 2011: 122-126.

[10] Junejo A K, Xu Wei, Mu Chaoxu, et al. Adaptive speed control of PMSM drive system based a new sliding-mode reaching law[J]. IEEE Transactions on Power Electronics, 2020, 35(11): 12110-12121.

[11] Nguyen A T, Rafaq M S, Choi H H, et al. A model reference adaptive control based speed controller for a surface-mounted permanent magnet synchronous motor drive[J]. IEEE Transactions on Industrial Electronics, 2018, 65(12): 9399-9409.

[12] Li Hongkui, Wang Qinglin. Self-tuning controller for servo motor with an adaptive disturbance observer[C]// 2nd International Conference on Advanced Computer Control, Shenyang, 2010: 277-281.

[13] Blanken L, Boeren F, Bruijnen D, et al. Batch- to-batch rational feedforward control: from iterative learning to identification approaches, with application to a wafer stage[J]. IEEE/ASME Transactions on Mechatronics, 2017, 22(2): 826-837.

[14] Li Liyi, Pei Genji, Liu Jiaxi, et al. 2-DOF robust∞control for permanent magnet synchronous motor with disturbance observer[J]. IEEE Transactions on Power Electronics, 2021, 36(3): 3462-3472.

[15] Fan Shicai, Luo Wuqiao, Zou Jianxiao, et al. A hybrid speed sensorless control strategy for PMSM based on MRAS and fuzzy control[C]//Proceedings of the 7th International Power Electronics and Motion Control Conference, Harbin, 2012: 2976-2980.

[16] 王伟颖. 永磁同步电机抗负载扰动控制策略研究[D]. 浙江: 浙江大学, 2012.

[17] 许彦卿. 基于扰动观测器的永磁同步电机调速系统控制[D]. 南京: 东南大学, 2016.

[18] Cui Peiling, Zhang Dachuan, Yang Shan, et al. Com- pensation based on time-delay control and internal model control for a gimbal system in magnetically suspended CMG[J]. IEEE Transactions on Industrial Electronics, 2017, 64(5): 3798-3807.

[19] Chai Shan, Wang Liuping, Rogers E. A cascade MPC control structure for a PMSM with speed ripple minimization[J]. IEEE Transactions on Industrial Electronics, 2013, 60(8): 2978-2987.

[20] de Angelo C, Bossio G, Solsona J, et al. Mechanical sensorless speed control of permanent-magnet AC motors driving an unknown load[J]. IEEE Transa- ctions on Industrial Electronics, 2006, 53(2): 406- 414.

Torque Disturbance Suppression Strategy of Permanent Magnet Direct Drive Servo Motor Based on Improved Reduced Order Observer

11211

（1. School of Automation Nanjing University of Aeronautics and Astronautics Nanjing 211106 China 2. 724 Research Institute China Shipbuilding Industry Corporation Nanjing 211106 China）

Due to the direct drive characteristics of the permanent magnet direct drive motor, the stability of the motor speed is greatly affected by torque disturbance, and the motor speed fluctuates violently affected by the cogging torque when running at low speed. This paper analyzes the disadvantage that the traditional proportional-integral speed control method cannot take into account both the tracking performance and the anti-disturbance performance. To this end, a traditional reduced-order state observer is introduced to estimate and feedforward the torque disturbance. The Bode plot and sawtooth wave response of the transfer function between the system disturbance torque and the real torque are analyzed, and the zero-pole cancellation is performed. Based on the principle, the transfer function is expected to be designed, and the differential unit is introduced to improve the traditional reduced-order observer. The sawtooth wave response of the improved observer is given and the improvement of the compensation response speed is demonstrated. A feedforward compensation method is proposed. An experimental platform for perturbation suppression of permanent magnet direct drive servo motor is built. Simulation and experiments verify that the improved reduced-order observer has good performance in suppressing compensation resonance, and has strong anti-disturbance ability, which can achieve stable operation under large disturbance and low speed.

Reduced order observer, permanent magnet servo motor, direct drive, torque dis- turbance suppress

10.19595/j.cnki.1000-6753.tces.211801

TM351

2021-11-05

2022-01-24

卜飞飞 男，1984年生，副教授，硕士生导师，研究方向为航空电源、伺服驱动、电机及其控制等。E-mail: bufeifei1984@163.com（通信作者）

郭子韬 男，1998年生，硕士研究生，研究方向为伺服驱动控制。E-mail: guozitao@163.com

（编辑 陈 诚）