传热学思维在本科教学过程中的培养

张欣宇，杨晓宏，温彩凤，高虹，包道日娜，贾彦

（内蒙古工业大学能源与动力工程学院，内蒙古呼和浩特 010051）

传热学是一门应用性和实践性较强的专业技术基础课，是能源动力类、机械类、材料类、土木类等专业的必修课。目前该课程已获批内蒙古自治区线下一流本科课程，已申报国家一流本科课程。课程内容主要包括热传导、热对流、热辐射和综合传热过程及应用四个部分，各部分之间密切联系又相互独立。实际传热过程分析需要运用数学理论和数学语言对传热现象进行理论分析，对复杂传热问题进行合理的抽象、概括、简化和理想化。学生通过学习传热学基本理论、基本方法和相应的计算方法，具备解决工程传热问题的基本能力，同时通过传热学实验技能训练，使学生具备主要热工参数的测量方法及初步的实验技能。

杨世铭、陶文铨编著的《传热学》（第五版）作为国内面向能源动力类的技术基础专业课书籍，其教学内容丰富全面。教师讲授过程中根据不同专业培养要求，侧重点略有不同，但授课过程中均涉及大量的公式推导和传热模型简化分析，教材中的整体内容根据热量传递方式分块展开细述，抽象难懂、理论计算公式复杂，同时涉及大量的高等数学、大学物理、工程热力学、工程流体力学等知识。为使学生全面掌握课程中涵盖的各章节知识点，并将知识点融会贯通，在学习过程中逐渐培养学生的传热学思维是非常必要的。

1 通过传热学分析方法促进传热思维的建立

传热学主要是通过温度场的分布和热量传递的速率分析热量传递的规律。在近两个世纪的发展过程中，形成了以分析解法、实验法、数值计算三类为代表的传热学研究方法。在本科生的教学过程中，培养学生通过传热学分析方法促进自身传热思维的形成尤为重要。

1.1 导热问题的分析方法——热阻网络图

由于物体中各点的温度受能量方程的偏微分方程所制约。应用数学分析的理论，求解在给定条件下的偏微分方程，从而得出确定物体各点的速度、温度等的函数，称为分析解。由于实际传热问题的复杂性，目前只能对比较简单的几何形状导热问题采用分析解。介绍分析解法的基本步骤与思路，对培养学生利用基本原理分析复杂实际传热问题十分有帮助。

（1）以一维稳态的单层平壁导热为例。

《传热学》第五版[1]2.3.1 是通过平壁的导热，导热系数是常数，平壁厚度为δ、没有内热源，两表面均维持均匀恒定温度t1、t2。取坐标如图1所示，利用分析解法可以建立导热问题的完整的数学描写：

图1 一维稳态平壁的导热

通过导热微分方程结合具体的定解条件组成了导热问题完整的数学描述。通过数学求解可以得到温度场的分布是呈线性的，热流量及热流密度沿平壁厚度方向是常数。这是一维稳态平壁导热的传热规律。

热量传递是自然界中的一种转移过程，与自然界中的电量的转移、动量的转移、质量的转移有类似之处。各种转移过程的共同规律性可归纳为：过程中的转移量等于过程的动力与过程的阻力之比[2]。在电工学中的欧姆定律有类似的规律，这种规律对平壁热传导可表示为：

在这里t为平壁两侧的温差，也是热量传递的驱动力，Rλ为热量传递过程的导热热阻。可以用热阻网络图的形式表示一维稳态无内热源的导热过程。

（2）拓展为一维稳态的多层复合壁导热。

如图2所示为多层复合壁的导热，采用耐火层、保温砖层和普通砖层叠合而成的锅炉炉墙的多层复合壁。忽略层与层之间的接触热阻，因此在层间分界面不发生温降。若各层厚度为δ1、δ2、δ3，各层导热系数λ1、λ2、λ3以及多层壁两外表面的温度t1、t4，根据串联过程的热阻叠加原则：总热阻等于串联过程各个分热阻之和[1]。如图3所示，利用热阻网络图法可以得到多层壁的热流量：

图2 一维稳态多层复合壁导热

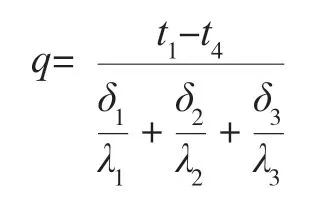
图3 相变储热的传热过程

通过一维稳态多层复合壁的导热分析，鼓励学生举一反三进一步扩展知识的应用。分析具体的一维稳态无内热源的传热过程，采用热阻网络图的方法是学生非常容易理解的。在讲授过程中，将一个单层壁的导热扩展为多层复合壁的导热，进而分析冷热流体通过复合壁的传热过程构成了连贯的知识体系。在进行复杂的计算时，灵活地使用热阻、热阻叠加原理，使计算过程不仅简单而且计算结果准确[3]。

1.2 对流换热的实验分析方法——实验关联式

通过实验的方法获得表面传热系数的计算式是求解对流换热的主要方式。为了减少实验次数、提高实验测定结果的通用性，传热学的实验测定是在相似原理的指导下进行的。根据相似原理的基本内容：凡是相似的物理现象，描写该现象的同名特征数（即准则数）相等。应用相似原理来安排与整理实验数据时，个别实验得出的结果可以代表整个相似组。对流换热的实验数据可以表示成相似准则数之间的函数关系。以管内单相强制对流换热为例，表面传热系数受到6 个因素的影响，如果每个变量各变化10 次，其他5 个保持不变，共需要106次实验。引入准则数，每个准则数是几个影响因素复合在一起综合反映一个物理现象的特征。此时，Nu数与Re数及Pr数有关，即实验关联式为Nu=f（Re,Pr），因此应当以Re数及Pr数作为实验中区别不同工况的变量，以Nu数为因变量。如果每个变量改变10 次，则总共仅需要做102次实验。可见应用相似原理指导实验可以减少实验次数，同时得到的实验关联式适用范围可以推广到整个相似组。因此，相似原理指导下的实验分析法是传热学中研究对流换热的主要方法。

1.3 传热过程的数值计算方法——CFD 模拟

数值计算法，把原来在时间和空间连续的物理量的场，用有限个离散点上的值的集合来代替，通过求解按一定方法建立起来的关于这些值的代数方程，从而获得离散点上被求物理量的值[4]。这种方法在很大程度上弥补了分析解法的缺点，适应性强，特别对于复杂问题更显其优越性，与实验法相比成本低。由于传热学基础理论比较晦涩难懂，特别是包含多种热量传递方式的具体的传热过程，采用传统的教学方法达不到预期的教学效果。在授课过程中，教师可以借助CFD数值计算[5]结果将动态的传热现象展示给学生。

如图3为相变储热的传热过程温度及液相率的云图，管内热流体水（HTF）从上而下的流动过程，沿程以对流换热的方式将热量传给管内壁，再由内壁以热传导的方式传给管外的翅片，而后将热量以导热和自然对流的方式传给相变材料石蜡（PCM），经过一系列的传热过程，热量由水传到石蜡，由于水流动沿程与管壁的温差逐渐减小，因此沿程换热减弱。通过这样的模拟云图引导学生分析传热过程及换热方式，找到传热不利的问题所在，流体侧对流换热较小也是影响传热的关键问题，接下来引导学生思考如何解决问题，想要达到传热强化的目的需采取什么样的措施。授课过程一方面锻炼学生识图读表的能力；另一方面培养学生细致的观察能力去发现问题、分析问题、解决问题。鼓励学生采用传热学原理解决在管子下部换热不利的问题，思考是否可以采取翅片数量和翅片长度的梯级变化布置从而解决换热不均问题。

在本科传热学讲授过程中结合数值模拟CFD 方法，将动态过程以及彩色结果以画面的形式展示出来，能充分调动学生学习的积极性，直观的传热过程促进了学生对传热知识的理解[6]。课堂上传授一部分CFD软件的应用入门知识，使学生能够独立地将掌握的数值分析方法应用到具体的传热过程，动手模拟探索生活和工程中的传热现象，如果在模拟过程中遇到问题，便会主动查找书籍资料探究其原因，这样的学习模式不但能增加课堂生动性，提高学生的学习积极性，同时也得到了事半功倍的效果。

2 通过课后习题资源培养传热学思维

《传热学》第五版课后丰富的思考题和习题贴近生活和工程应用实践，新增了MATLAB 小程序，学生可通过扫描图中二维码识别程序代码。传统的理论教学通常采用“PPT+板书”的模式，教师可以通过虚拟MATLAB模拟实验展示计算结果。将班级学生划分小组进行自主选题，邀请学生参与演示，小组之间讨论互评结果。

以第二章稳态热传导2.3.4 中电熨斗的一维稳态导热为例，为使学生形象认识电熨斗底板温度的变化，根据能量守恒原理，电熨斗的加热量全部用于对环境的对流散热和辐射散热。在授课过程中应用MATLAB 程序进行演示，学生可以扫描课后二维码识别程序代码，然后通过参数赋值得到结果，也可以对程序进行改写获得更多的结果，加深对不同边界条件下传热过程的认识。通过图像分析电熨斗底板温度的变化，加深学生对热量传递的理解，激发学生学习兴趣和科研乐趣。采用MATLAB 编写程序进行热计算应用于传热学习中，对于学生后续专业课程及毕业论文的计算都能起到较好的作用。

3 通过实验课程促进传热学思维的形成

目前能动类专业传热学开设实验为：圆球导热仪测定黄砂导热系数实验、强制对流管外换热实验、角系数测定实验和铂丝表面发射率测定实验，依次对应热传导、对流换热和辐射换热的理论教学部分。实验内容简单易操作，适合本科学生。针对实验所对应的理论内容讲授完毕，接着布置实验作为验证，使理论与实验在时间上有很好的衔接，更好地促进学生对知识的理解与掌握。将学生设计初步的实验方案，与实验教师给定的参考方案进行对比分析，最后完善最终的实验方案。这样的三步法使学生将所学理论知识充分应用，小组学生互相讨论、分析、预测结果，在学习的同时锻炼了学生的团队协作能力，测试数据的记录、实验报告的整理、全过程的实战促进了知识的应用和掌握。

4 促进传热思维培养行之有效的策略

（1）采用思维导图的方式将基本概念、基本原理、物理量进行整合梳理，建立知识点之间的联系与区别，前后学习融会贯通。

（2）采用软件对知识进行实际操作应用。在具体应用的过程中更深刻地理解知识。例如采用CFD 进行数值模拟，利用MATLAB 进行编程计算实现传热计算。

（3）将班级学生进行分组，布置小算例教学任务。学生分别上讲台展示作业，其他学生提问评价。培养学生的表达能力、知识运用能力，激发学生的学习热情。

（4）学生对知识的有效反馈是教师教学效果的自我评估。可以通过线上上传热热点问题的讨论、课前问答、课后作业等多种方式增加师生互动。将传热学的应用前沿融入课堂基本知识的讲授中，增强学生学习兴趣。

5 结语

在传热学的教学过程中，对热传导过程采用热阻网络图进行分析，对流换热采用相似原理指导下的实验关联式，传热过程采用数值模拟分析法。对于复杂传热问题，借助CFD 方法进行数值计算和演示，通过MATLAB小程序进行热计算，帮助学生掌握流体流动与传热的基本规律，加深对数值计算方法的理解。传热学思维的培养贯穿于整个传热学的学习是至关重要的。