软土地区浅埋矩形顶管施工地表变形与数值模拟研究

毛祖夏，王国权，孙宝生，李佳明，黄 磊，陈式轩

(1.宁波市鄞城集团有限责任公司，浙江 宁波 315000；2.宁波市城建设计研究院有限公司，浙江 宁波 315000)

顶管法作为一种非开挖的技术，可以显著降低对周边环境以及地面交通的影响，其在污水管网、综合管廊等地下工程得到大量应用。矩形顶管较圆形顶管有更高断面利用率，能更好的适用浅覆土工况，常用于城市地下联络通道。但相较圆形顶管，其弊端在于更易受到掌子面支护压力、注浆压力、管土摩阻力、背土效应、超挖、欠挖等因素的影响，易造成地表及临近管线下沉或隆起，甚至会造成地下空洞问题，从而引发地面塌陷。国内外学者对矩形顶管开展了一些研究。有学者对软土地区的实测数据进行分析，结果表明：地表前期隆起越大，则相应最终沉降越小，最大沉降位于始发井周围；顶推力造成地表隆起，土层损失造成地表下沉。基于理论方法进行分析，结果表明：地表隆起的主诱因是正面附加推力，其次为顶管机及后续管节造成的摩阻力。通过理论、实测与数值计算的分析方法对施工阶段多因素进行研究，结果表明：地层损失对地表沉降影响较大，摩阻力次之，注浆有助于地表抬升。分析了摩阻力、掌子面附加应力、地层损失的共同作用，提出矩形顶管地层位移计算方法，表明地表隆起主要是附加应力、摩阻力，沉降则是地层损失造成。通过ABQUES模拟浅层顶管顶进，并与实测对比分析，结果表明：浅埋顶管施工，地表为整体沉降，侧摩阻力和推力共同引发了短时间地表隆起。通过理论、数值模拟和实测数据3方面对顶管施工引起的临近地铁隧道展开研究，认为地层损失是引发隧道变形的主要原因。

目前，矩形顶管相关研究分析主要集中在深埋情况，对于软土地基浅埋大断面的矩形顶管深入研究较少。本文依托宁波市鄞州区医药学校地道顶管工程，通过对实测数据与数值模拟及相关影响敏感性参数进行分析，进一步完善浅埋大断面顶管施工对地表沉降理论分析，可为相关工程提供设计依据及施工技术参考。

1 工程概况

1.1 工程简介

工程位于宁波市鄞州区鄞县大道东段，北侧为浙江医药高等专科学校，南侧为浙江万里学院，通道横穿鄞县大道，主通道段全长67.5 m，采用矩形顶管工艺施工，共45节，单片管节长度为1.5 m，管节尺寸为6.0 m×3.3 m(内部净宽×净高)，壁厚为45 cm，管节混凝土强度等级为C50，顶管最小覆土仅为4.5 m。顶管平面和标准断面如图1、图2所示。

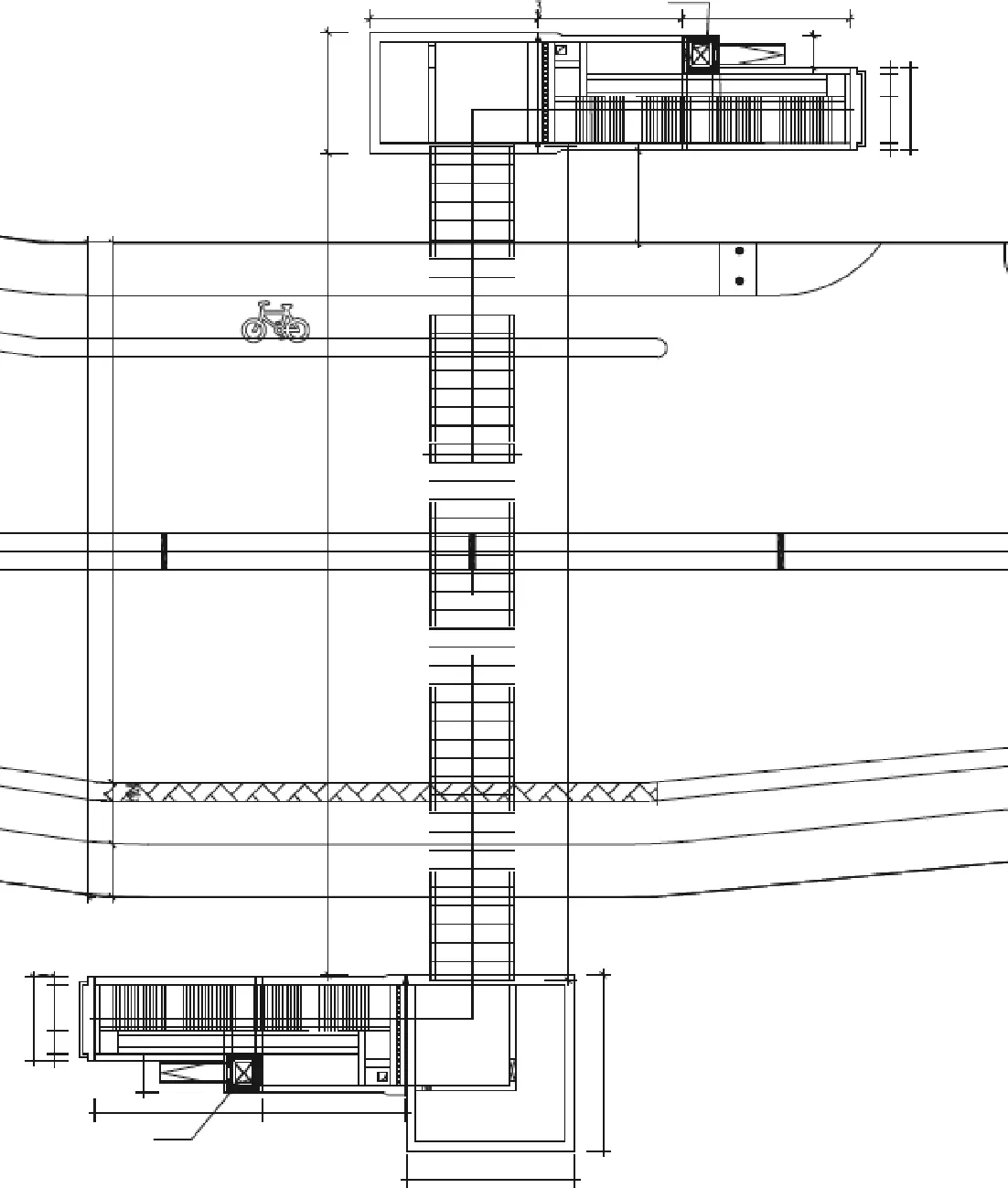
图1 顶管通道平面图Fig.1 Cross section view of pipe jacking channel

图2 顶管通道横断面图Fig.2 Cross section view of pipe jacking channel

1.2 工程地质条件

根据本工程提供的地勘报告，顶管施工区域为滨海相淤积平原，主要土层包括为杂填土、黏土、淤泥质黏土、淤泥、粉质黏土，顶管穿越土层主要涉及黏土、淤泥质黏土、淤泥；各土层物理力学参数如表1所示。

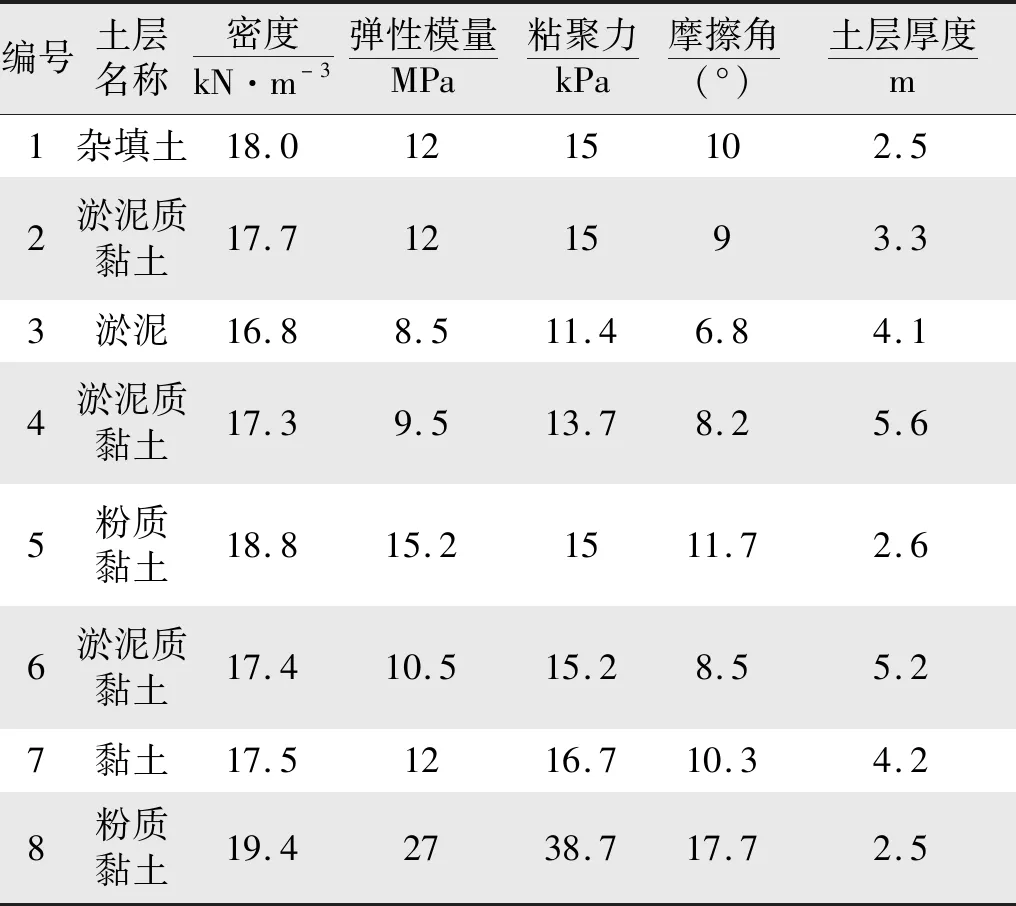
表1 土层物理力学参数表Tab.1 Physical and mechanical parameters table of soil layer

1.3 施工监测方案

顶管上方为鄞县大道，是城市主干道，车流量密集，因此需防止顶管施工期间路面产生较大的沉降或隆起变形。为全面观测施工期间路面的变形情况，在顶管上方地表共设置了21个监测点；共3个断面，每个断面设7个监测点；点位沿顶管轴线对称布置，横向间距3 m，编号为D1～D21，具体如图3所示。3个断面分别距离顶管始发位置为24、33和42 m。

图3 地表沉降监测点位平面图Fig.3 Plan of monitoring points for ground subsidence

2 数值模型

2.1 模型假设

数值模拟的实质是将复杂而抽象的问题简单化，针对问题的关键因素进行研究，本文主要研究顶管施工过程中地面的沉降规律，结合其他研究人员对顶管施工数值模拟的研究成果，现对模型作如下假设：

(1)假设地面是水平的，且各地层分界面均平行于地表；

(2)假设各土层土体均为均质、各向同性、理想弹塑性体；

(3)土体在顶管施工前为稳定状态，模型中设定初始状态下的地面沉降为零；

(4)不考虑施工过程中的时间效应，仅以顶管管片位置的变化来反映顶进过程；

(5)假设作用于掌子面的压力为定值，并简化为作用在掌子面的均布荷载。

2.2 模型参数

本文土体选取Drucker-Prager模型(以后简称D-P模型)作为本构模型(本构模型的确定见后文4.1部分)，对顶管施工过程进行分析。D-P模型下土体的粘聚力及内摩擦角采用本工程提供的地勘报告，并通过式(1)和式(2)进行换算，换算后各土层物理力学参数如表2所示。

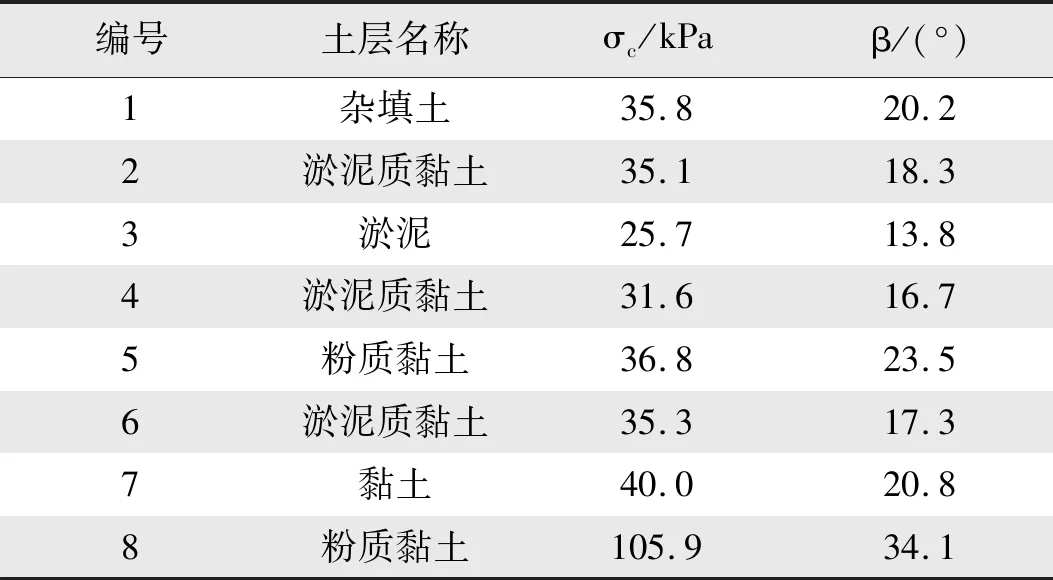
表2 D-P模型下的土体物理力学参数表Tab.2 Physical and mechanical parameters table of soil layer under the D-P model

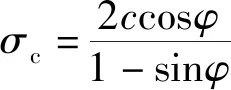
(1)

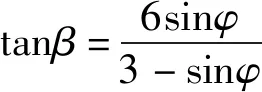
(2)

式中：、分别为D-P模型下的粘聚力和内摩擦角；、分别为M-C模型下的粘聚力和内摩擦角。

顶管管片采用C50钢筋混凝土，机壳为钢结构，注浆体为水泥浆液，模型中均为弹性体；各材料物理力学参数如表3所示。

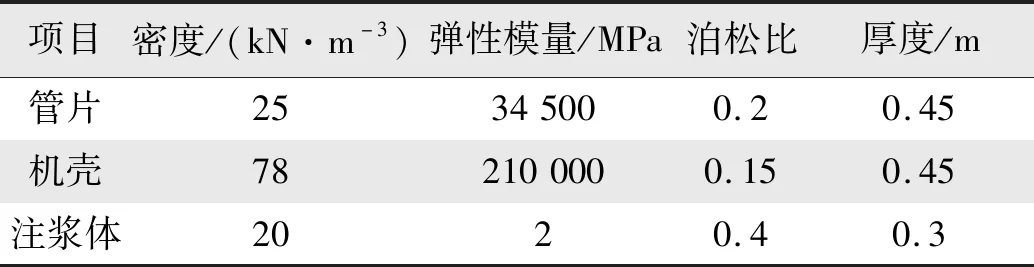
表3 结构物理力学参数表Tab.3 Physical and mechanical parameters table of structure

掌子面土压力计算值为=10kPa，模型中取掌子面处均布压力为=12=126 kPa。管片与土体之间摩阻力取=8 kPa。

2.3 模型建立

采用有限元分析软件Midas GTS NX进行建模分析，结合以往工程经验，在顶管以外3～5(为管片长边尺寸)处，施工对土层的影响有限，故取模型宽度66 m，高度30 m，长度取顶管段长度67.5 m。

土体及注浆体采用实体单元，顶管机壳及管片采用板单元，模型网格划分后得到94 551个单元和61 488个节点，模型如图4所示。

图4 数值模型示意图Fig.4 Schematic diagram of numerical model

2.4 模拟过程

将顶管顶进过程划分为多步骤进行模拟，以实现顶管顶进的动态过程，全过程共分为47个施工阶段，包含初始应力阶段+45个顶管顶进阶段+贯通阶段，每顶进一节管片设为一个施工阶段，假设每个施工阶段是瞬时完成的。Midas GTS NX中对土体的开挖是通过对单元的激活和钝化来实现的，模型的具体模拟过程如下：

(1)初始应力阶段，激活全部土体单元及边界约束，并采用重力加载形成初始地应力，设置初始应力状态下土体沉降为零；

(2)顶进阶段(顶管机进入)，钝化该阶段开挖土体，激活顶管机壳，并施加掌子面支护力及机壳与土体之间的摩阻力；

(3)顶进阶段(管片进入)，钝化该阶段开挖土体，钝化前一阶段的机壳及掌子面支护力，激活现阶段顶管机壳、掌子面支护力及顶管机尾部顶管管片；

(4)重复阶段3，直至顶管完成。

3 数值模拟结果

3.1 纵向地表沉降分析

图5～图7分别为顶管过程中监测点D4、D11、D18处地表变形监测值与模拟值对比图。从图5～图7中可以看出以下几点：

图5 监测点D4竖向沉降曲线图Fig.5 Vertical settlement curve of monitoring point D4

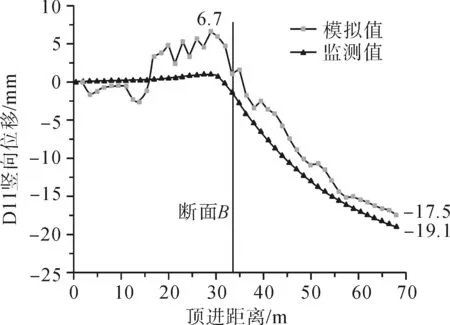
图6 监测点D11竖向沉降曲线图Fig.6 Vertical settlement curve of monitoring point D11

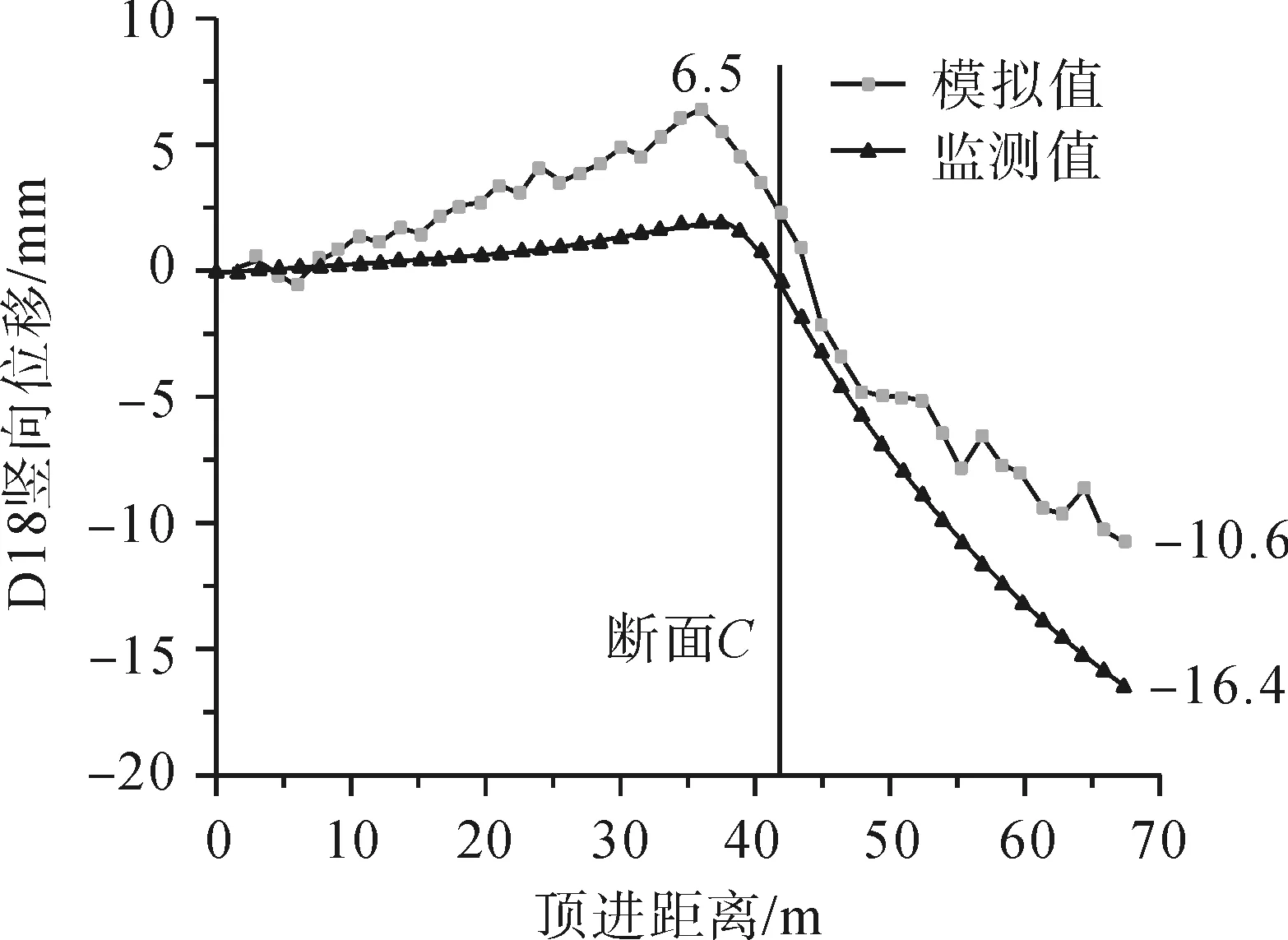
图7 监测点D18竖向沉降曲线图Fig.7 Vertical settlement curve of monitoring point D18

(1)各监测点变形的模拟曲线呈现出与监测曲线相似的变化趋势，两者吻合较好，说明了模拟结果的可靠性。各点位沉降变化曲线总体上表现为先隆起、后沉降的变化规律。实测沉降转折点在机头顶进到距离监测断面4.5～6 m的位置；而模拟结果中出现明显沉降趋势的转折点均在顶管机头距离监测断面4.5 m处，与监测结果也较为吻合；

(2)从最终沉降量可以看出，D4监测点已基本趋于稳定，D11监测点也即将趋近平稳；而D18监测在顶管结束后仍保持着一定的沉降速度，这是因为D4监测点距离始发井最近，最先出现沉降，随着顶管机头的顶进，当机头距离监测点一定距离(本工程约40 m处)时，顶管施工对该监测点的影响有限。而D18距离接收通道不足40 m，故顶管结束时沉降仍未达到稳定状态；

(3)在实测数据中，各点最大隆起值分别为4.5、6.7和6.5 mm，最大沉降值分别为-27.9、-17.5和-10.6 mm；表现为离始发井越远，最终隆起量越大，而最终沉降量越小。在模拟结果中，D4无隆起量，D11和D18有较小隆起量，分别为1.0、2.0 mm；最大沉降值分别为22.9、19.1和16.4 mm。从沉降曲线可以看出，模拟值与实测值吻合较好；而从隆起量可以看出，两者之间有一定的差别。

根据文献[12]、文献[13]模拟结果可以看出，各点位均体现出先隆起，后沉降的变化规律。针对本文中D4监测点无隆起的现象，认为其原因在于本工程土质较差所致。因基本为淤泥质黏土，局部为淤泥，该部分土体强度较低，且具有高压缩性，受顶推力扰动影响，土体颗粒重排列，颗粒间孔隙水消散，软土层自身压缩变形较大，从而引起地表变形较小，不足以抵消因顶管施工引起的沉降，故该点位未能体现出隆起量。为了证实上述观点，现对土层参数进行改良，统一提高土层参数，取=30 kPa、=20°；相应D-P模型下=85.7 kPa、=37.7°，由此得到的模拟结果如图8所示。

图8 土体改良后各监测点竖向沉降曲线图Fig.8 Vertical settlement curve of each monitoring point after soil improvement

从图8可以看出，对土体进行改良后，各监测点均出现了较为明显的隆起量，由此证实了上述观点。

3.2 横向地表沉降分析

图9～图11分别为顶进60 m时断面A、B、C处沉降槽曲线实测值与模拟值对比图。

图9 断面A沉降曲线图Fig.9 Settlement curve of section A

图10 断面B沉降曲线图Fig.10 Settlement curve of section B

图11 断面C沉降曲线图Fig.11 Settlement curve of section C

从图9～图11中可以看出:

(1)所有断面的沉降实测值与模拟值均呈现出中间大，两边小的规律，即顶管中轴线上方地表沉降量最大；

(2)距离始发井越远，沉降槽越平缓，最终沉降量越小；

(3)距离中轴线18 m处沉降量已小于3 mm，可忽略不计，故可认为顶管施工对地面的影响范围在顶管中轴线两侧各2(为管片长边尺寸)范围内，对2范围外几乎无影响。

4 参数分析

4.1 土体本构模型影响

目前，岩土分析中涉及到的简单本构模型包括摩尔-库伦(Mohr-Coulomb)、德鲁克-普拉格(Drucker-Prager)，高级本构模型中修正剑桥(Modified Cam-Clay)、硬化土(Hard Soil)、硬化土小应变(HS-Small)等较为常见。

摩尔库伦模型和德鲁克-普拉格模型由于选用参数简单、易于获取，被广泛应用于岩土分析。但实际土体各参数的变化通常是非线性的，简单线弹性模型难以真实的反映土体变化过程，尤其是土体的硬化(软化)过程。修正剑桥模型是在软土基础上建立的本构模型，能够较好的体现土的非线性变化。硬化土和硬化土小应变模型是进一步考虑土体的压硬性和剪胀性特点，硬化土小应变模型在硬化土模型上增加对小应变区域内刚度随应变的非线性变化考虑，但目前该两种模型参数只通过地勘资料无法直接获得，各参数的选取存在大量经验关系，对不同的土体参数间关系差别过大，难以做到准确的选取。

本文中根据宁波软土特点，选取摩尔库伦模型、德鲁克-普拉格模型、修正剑桥模型、硬化土模型4种模型与实测结果进行分析。

图12为D11监测点不同模型下模拟值与实测变形对比结果。

图12 不同本构模型下D11沉降曲线图Fig.12 Settlement curves of D11 under different constitutive models

由图12可以看出，修正剑桥和德鲁克-普拉格模型的计算值与实测值相符程度最高，均能较为准确的反映实际施工过程；而其余模型与实际结果偏差过大。

这主要是因为本构关系与土体特性是相关的，该项目施工区域土层以软土为主，摩尔库伦模型难以描述软土变化非线性变化过程，因此难以体现土体变形过程。硬化土模型考虑压缩硬化和剪切硬化，但地勘报告中通常未能给出所需的割线模量、卸载模量等参数，主要依赖经验进行参数选取。目前未有宁波地区关于硬化土参数经验取值方面的相关研究，本文借鉴的是上海地区的经验取值，这极大地影响了模拟效果，除此之外硬化土模型在软土上的适用性仍存在缺陷，事实上软土地基在不断加载和卸载过程中，可能会显著出现软化和液化的问题，硬化土模型并不能很好考虑该特性。

4.2 地层损失影响

理想的顶管过程，是能够在顶进过程中始终保存保持管节尺寸与开挖尺寸相等。而现实中顶管机开挖断面大于管节断面，工程上会采用注浆形成泥浆套拟弥补空隙和减小顶进阻力，但往往会遇到泥浆套形成困难，管土接触不佳，造成背土作用，反而使得前方管节外轮廓大于后方管节，进一步加大空隙，形成土层损失。在Midas GTS和Plaxis中可以通过对管片施加收缩，来模拟隧道洞室断面面积的减小，收缩用百分比表示，代表减小的面积占原先外部管片面积的比例。收缩断面示意图如图13所示。

图13 收缩断面示意图Fig.13 Schematic diagram of reduced section

以监测点D11为例，通过设置不同断面收缩模拟不同地层损失差异，模拟结果如图14所示。

由图14可以看出，随着断面收缩的加大，顶管机未到达监测点前隆起量降低；这是因为本来受掌子面压力向斜上方隆起的土体，为弥补顶管机与管片尺寸差异造成的土层损失，土体向地层损失区域移动，从而降低了地表隆起量。当顶管结束时，最终的沉降量有所增加而且会高于降低的隆起量；这实际上是由于断面收缩(地层损失)加大，导致受到扰动的土体程度越深，范围越广，后期沉降也就越大。

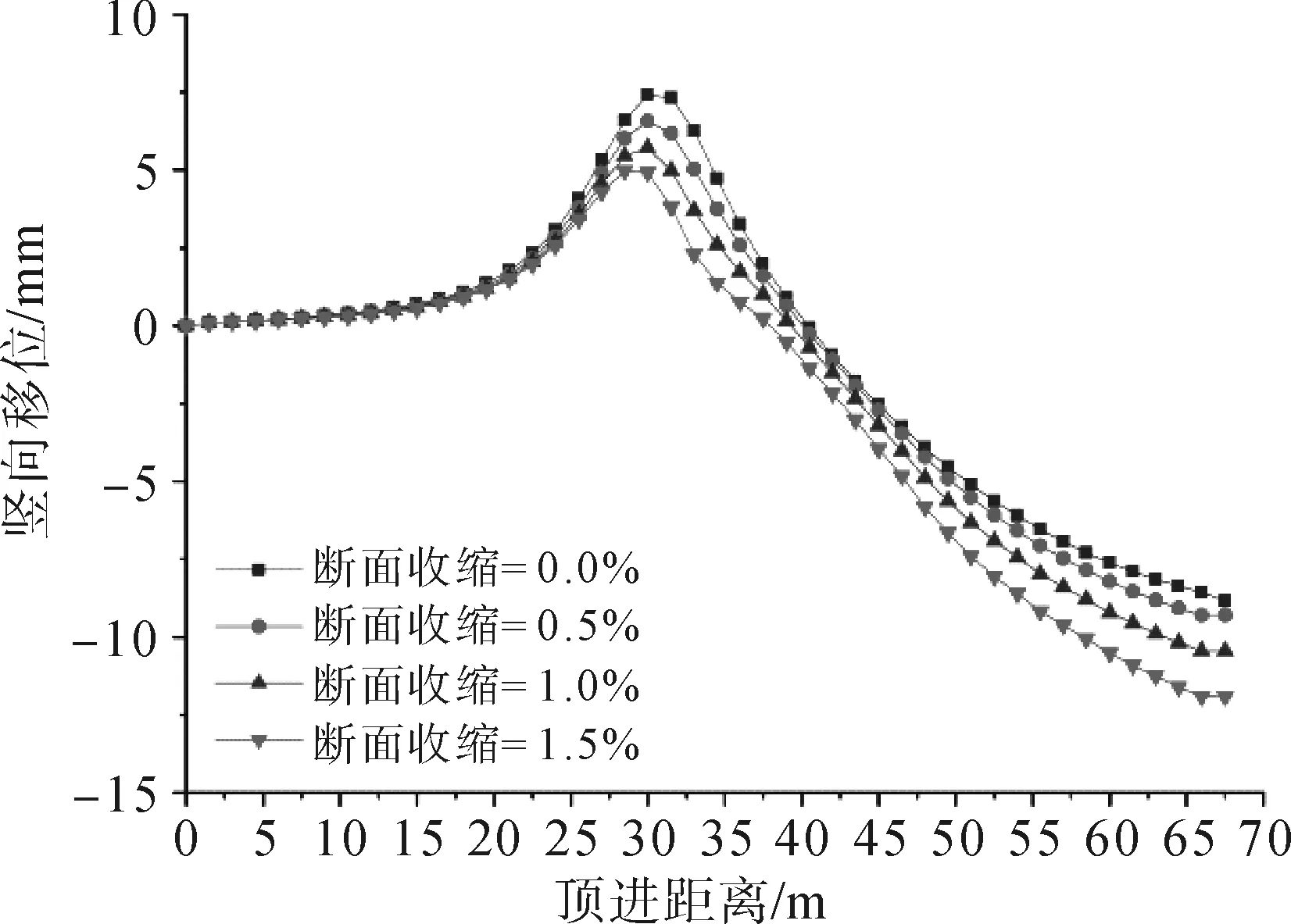
图14 不同断面收缩下D11沉降曲线图Fig.14 Settlement curve of D11 under different section contraction

4.3 掌子面压力影响

为研究掌子面不同压力对地表变形的影响，取压力值分别为0.75、1.0、1.2、1.5、2.0进行计算。图15为不同压力下，D11监测点在顶进过程中的位移对比图。

图15 不同掌子面压力下D11沉降曲线图Fig.15 Settlement curve of D11 under different face pressure

从图15可以看出，当掌子面压力小于理论计算土压力时，地表在开挖全过程始终保持下降趋势，随着压力增大，监测点最终沉降量越小，而期间产生的最大隆起量越大，且呈现出随着压力的增大，隆起量增加越明显的趋势，说明掌子面压力对地面的隆起量有较大影响。从监测数据来看，该监测点出现较大隆起可能是顶进过程中掌子面压力较大所致。

综合比较5种掌子面压力下的地表沉降曲线，对于宁波软土地区结合数值分析和项目经验建议取1.2倍理论土压力作为掌子面压力，既能避免造成前期的过大隆起，又能有效的控制地表的最终沉降。

4.4 管土摩阻力影响

管土摩阻力是引发土体扰动和背土效应的主要诱因，在工程中常采用减阻注浆的方式，减小管土间的摩阻力，以减小对周边环境的影响。

图16为不同管土摩阻力的下D11的竖向位移变化。

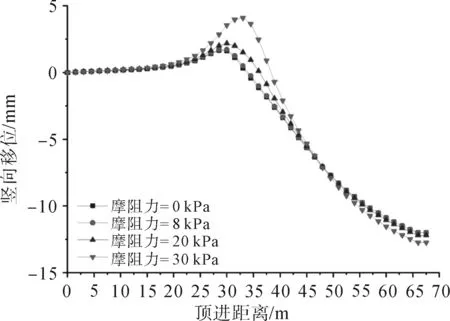
图16 不同管土摩阻力下D11沉降曲线图Fig.16 Settlement curve of D11 under the different friction between pipe joint and soil

从图16可以看出，摩阻力越大，地面前期隆起加剧，后期沉降增加。导致这种现象主要是因为管土间的摩阻力过大带动周围土体移动，顶管机后方土体随管节向前移动，从而使得前方隆起加剧；而后方土体地层损失增加，最终沉降加大。

5 结语

依托宁波市鄞州区医药学校地道顶管工程实例，通过对实测数据和数值模拟结果进行对比，并对外部因素和施工因素进行分析，得到如下几点结论：

(1)借助Midas GTS有限元软件，对多种土体本构模型进行试算并与实测结果进行比较，结果表明：土体采用修正剑桥本构或Drucker-Prager本构模型所计算出的结果与实际相比较更为合理。其中土体采用Drucker-Prager本构模型与实测结果对比，两者拟合程度较好，数值模拟能够较好地反映实际施工过程中的地表变形；

(2)地表沉降主要发生在顶管中轴线两侧各2(为管片长边尺寸)范围内，其余区域无明显沉降。故在软土地区类似工程项目中，应加强对顶管轴线两侧各2范围内地面的变形监测；

(3)顶管掌子面压力是引起地表隆起的主要原因，对于宁波软土地区的顶管施工，建议掌子面压力取1.2倍理论土压力。此外当泥浆套不理想的情况下，管土之间摩阻力较大，对于浅埋顶管易于发生背土效应加剧地表的隆起，施工中应采取有效的减摩措施。