融合PCA的改进ICP激光点云配准算法

王太学，江智，江德港，李柏林，郭彩玲

(1.西南交通大学 唐山研究生院，河北 唐山 063000；2.西南交通大学 机械工程学院，成都 610031；3.唐山学院 河北省智能装备数字化设计及过程仿真重点实验室，河北 唐山 063000)

0 引言

点云配准是将不同视角下获得的点云数据经过一定的旋转平移变换到同一坐标系下的过程，广泛应用于计算机视觉[1]、三维重建[2]等领域。

目前国内外学者已经对点云配准进行了大量研究。最经典的点云配准算法是Besl等[3]提出的迭代最近点(iterative closest point，ICP)算法，该算法的配准前提是要求输入点云有较好的初始位置，才能实现精确配准，但是算法本身需要多次迭代，收敛速率较慢，并且容易陷入局部最优。针对经典ICP算法的缺点，相关学者对ICP算法进行了改进。赵夫群等[4]将三维点云转换成二维方位角，通过二维图像和三维点的映射关系进行坐标变换，最后基于奇异值分解完成了ICP算法的精配准；严剑锋等[5]基于点云的几何特征利用点云的曲率提取特征点，通过匹配特征点对完成粗匹配，为ICP算法提供较好的初值，提高了配准精度和可靠性。点特征直方图(point feature histogram，PFH)和快速点特征直方图(fast point feature histogram，FPFH)[6-7]虽然在点云配准的过程中也能提高点云配准的精度，但是当点云体积密度较大时，点云配准效率会大大降低。马伟丽等[8]通过随机抽样一致性算法结合四元数法计算配准参数，完成了全局最优参数的点云精确配准，配准效率却有待提高；He等[9]提出一种基于PointNet++与ICP算法相结合的点云配准算法，同时提取多个点云特征，实现了点云的快速鲁棒配准，但是对于稀疏点云的适应性较差；Magnusson等[10]提出了3D-NDT(three-dimensional normal distributions transform)算法，把三维体素内的点云数据集转换成连续可微的概率分布函数，通过得分法实现点云的配准；Aiger等[11]提出了4PCS(4-points congruent sets)算法，算法无需初始位置和滤波去噪，并允许存在离群值；在4PCS算法的基础上，Mellado等[12]提出了super4PCS(super three-dimensional normal distributions transform)算法，运用仿射变换不变性，利用共面四点完成点云匹配；Chetverikov等[13]提出一种trimmed ICP(TrICP)算法，通过寻找最小重叠参数实现点云的精确匹配，但是需要具有良好的初始位置估计值。

基于以上学者的研究现状，为了改进ICP算法需要较好的初值和收敛速度较慢的问题，本文提出一种基于主轴基向量间的关系进行主轴校正的方法，利用两组点云的三个点云主成分坐标轴对应基向量间的关系进行主轴校正，为ICP算法输入较好的初值，接着针对具有部分重叠的点云提出一种改进ICP算法，利用最近邻算法搜索重叠点云部分的有效对应点对，利用有效点对进行求解最优变换参数完成点云的精确配准。

1 点云粗配准

1.1 主轴方向分析

PCA(principal component analysis)算法[14]是一种用于降维的统计方法，主要的作用是用来简化数据集，通过线性变换求取数据集的主成分，从而实现降维。两组点云数据经过PCA算法处理后得到了初始的旋转和平移矩阵。虽然其主轴基本共线，但仍然存在主轴方向相反的可能性[15]，需要对主轴方向校正才能为精配准提供较好的初值。

设两组点云P和Q经过PCA变换后得到的坐标轴分别为upvpwp、uqvqwq，原点分别为Op和Oq，其中u、v、w分别表示第一坐标轴、第二坐标轴和第三坐标轴。当对点云进行旋转和平移变换后，主轴方向出现相反的情况有7种，如表1所示，定义类别Ci(i=1，2，…，7)。其中“1”表示两组点云的两个对应坐标轴方向相同，“-1”表示两组点云的两个对应坐标轴方向相反。

表1 主轴方向相反情况

经过PCA后以两组点云的质心为原点建立相对坐标系，可能出现的点云坐标系情况如图1所示，其中图1(a)为点云Q的坐标系，图1(b)至图1(h)为点云P经过PCA后可能出现坐标轴反向的类型。

图1 PCA后出现反向坐标轴的类型

1.2 点云主轴校正

对于两组已经进行处理后的点云数据，主轴基本对齐后可能出现表1中7种类别的任何一种，主轴校正的关键就是确定出现的是哪一类别，针对这一类别进行主轴调整，得到较好的旋转和平移矩阵初值。

图2 确定主轴类别流程图

步骤1：输入两组相似点云。

步骤2：利用PCA进行点云数据处理，实现主轴对齐。

步骤3：利用SVD分解计算α、β和γ。

步骤4：计算αp·αq，若大于0，计算βp·βq，若大于0，计算γp·γq，若大于0，则主轴方向相同，若小于0，输出类别为C1；若βp·βq<0，计算γp·γq，若大于0，输出类别为C2，若小于0，输出类别为C3；若αp·αq<0，计算βp·βq，若大于0，计算γp·γq，若大于0，输出类别为C4，若小于0，输出类别为C5；若βp·βq<0，计算γp·γq，若大于0，输出类别为C6，若<0，输出类别为C7。

步骤5：根据步骤4的判断结果，对源点云P与目标点云Q主轴方向相反的坐标轴的基向量取反，即αp=-αp或βp=-βp或γp=-γp，从而完成Up校正，得到新矩阵UP0。

如图3(a)所示，为两组点云进行PCA处理后的点云配准情况。从图中可以看到，两组点云主轴已经基本对齐，但出现了主轴u和w反向的情况。经过算法初配准后的结果如图3(b)所示，实现了主轴方向的校正。

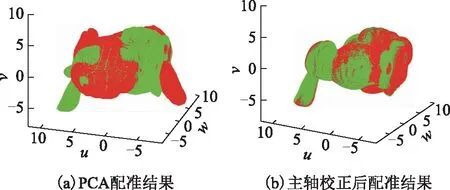
图3 点云粗配准图

2 点云精配准

两组点云在经过粗配准后，初始位置关系已经基本相近，运用经典ICP算法进行迭代，最小化目标函数求解最优变换参数R和T即可完成精配准。但是在实际点云数据获取过程中，不同视角下的两组点云在同一个坐标系下会有一定重叠度但是并不会完全重合[16]，使得ICP算法在应用时受限。

在点云配准的过程中，并不是所有点对对配准的贡献都相同[17]，非重叠区域的点在配准的过程中只会找到错误点对[18]，因此要剔除错误点对的影响。

针对具有部分重叠的点云配准问题，本文提出了改进ICP算法，先将两组点云进行粗配准，之后利用最近邻搜索算法寻找最近邻点组成有效点对，基于有效点对迭代求解最优变换参数完成配准。

2.1 改进ICP算法描述

2.2 改进ICP算法步骤

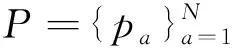
步骤2：建立两组点云的点对关系，表达如式(1)所示。

(1)

式中：ck代表一组点对关系；得到两组点云的有效点对，记为Dl{l=1，2，3，…，s}，s为有效点对的个数，l为一组有效点对，s≤N且s≤M。

(2)

其中，将粗配准得到的结果作为第一次迭代的初值，通过以上迭代步骤来获得最优解。

3 实验实例与分析

为验证本文算法性能，选取斯坦福大学点云数据库中Bunny模型为实验对象，其中源点云的数量为31 797(图4紫红色点云)，目标点云的数量为35 947(图4蓝色点云)。实验从初始位置和重叠度两个方面对点云数据进行配准实验，分别验证算法在粗配准和精配准过程的性能。实验环境为Intel Xeon Silver 4110 2.10 GHz CPU，运行平台为MATLAB R2016a。

3.1 粗配准

为检验本文粗配准算法性能，选取基于局部特征的配准算法FPFH、4PCS、PFH和改进PCA算法进行对比分析。图4(a)为点云的初始位置，图4(b)～图4(e)分别为FPFH、4PCS、PFH和改进PCA算法对点云进行粗配准后的结果，四种算法的均方根误差RMSE和所用时间如表2所示。

图4 粗配准测试

表2 粗配准算法结果对比

从实验结果可以看出，本文算法在配准时间和误差上优于其他三种算法。FPFH算法在配准时没有完全考虑中心点周围邻域的所有点对关系，使周围的一些几何信息丢失导致匹配误差较大；4PCS算法精度有所提高，但每次需要随机采样，并且点云重叠率低也会导致其配准时间增长；PFH算法需要计算邻域点所有组合的特征值，使算法复杂度增高，导致算法的配准时间较长且其平移误差较大。

3.2 精配准

为验证本文算法在不同重叠度下点云的配准性能，选取三组具有不同重叠度的点云与三种精配准算法TrICP、super4PCS、3D-NDT进行对比分析。本文算法能够自动计算出点云的重叠度，重叠度参数如表3所示(ε根据粗配准的结果设定为0.8)，配准后的结果如图5、图6和图7所示，不同重叠度下的配准误差和时间如表3所示。

图5 重叠度=0.092算法配准结果

图6 重叠度=0.684算法配准结果

图7 重叠度=0.671算法配准结果

表3 配准算法的效果比较

根据配准结果得出，对于不同重叠度的点云，本文算法在配准的时间和收敛误差上都明显低于其他三种算法，经过改进的PCA算法粗配准后，利用KD-tree寻找最近点，并利用欧式距离较大的有效点对进行精配准，缩短了配准时间和提高了配准的精度。TrICP算法对点云的初始位置要求较高，在寻找最佳重叠时需多次迭代配准，计算时间较长，并且在初始位置不好的情况下容易陷入局部最优得到错误匹配结果。super4PCS算法是对4PCS算法的改进，利用共面四点的仿射不变性进行点云配准。虽然其配准性能较高，但是需要人工选取样本点，当点云密度增大后算法配准效率会降低。3D-NDT算法对参数设置较敏感，需要多次手动进行参数的调整，而手动调参的过程也增加了算法时间的开销。

对比同一算法，从实验数据可以看出，重叠度相差较大的两组点云，重叠度越大，配准效率越高，而对于重叠度近似的两组点云，在保证良好初始位置的情况下，其配准效率也会越高。而本文算法在重叠率较低和初始位置相差较大的情况下收敛速度较快，配准精度较高，证明了本文算法的鲁棒性。

3.3 牵引座支座点云配准

为验证算法在实测数据上的性能，用FARO Design ScanArm扫描仪从不同方位获取了汽车牵引座点云数据，利用TrICP算法、super4PCS算法、3D-NDT算法和本文算法对实测点云数据进行配准，配准结果如图8所示，其中图8(a)为点云数据的获取过程，图8(b)为获取两组点云的初始位置，图8(c)～图8(f)分别为四种算法的配准图，并对局部的配准效果进行了放大，算法的均方根误差和耗时如表4所示。

图8 支座点云配准结果

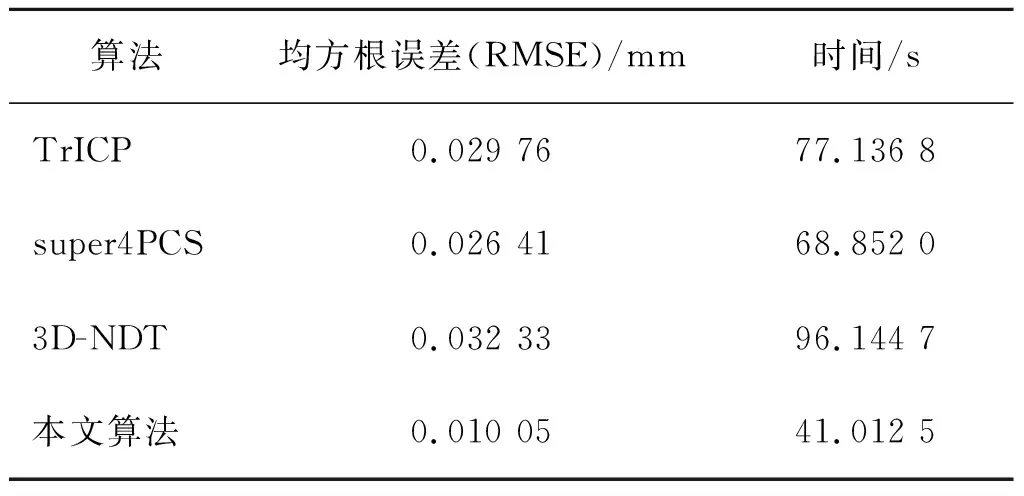
表4 不同算法对支座点云的配准结果

从配准结果和表中所得数据可以看出：3D-NDT算法表现最差，由于数据为实测数据，噪声不可避免，算法在参数选取过程中难度增加，误差增大；TrICP算法较3D-NDT算法在性能上有所提升，但受初始位置影响配准效果仍不理想；super4PCS算法虽然配准误差较3D-NDT算法和TrICP算法稍有提高，但是随着点云数量的增加，导致其选取样本点的效率降低而匹配时间增加；本文算法在利用欧式距离较大的有效点对配准过程中减少了配准时间并增加了配准精度，配准精度为0.010 05 mm，配准时间为41.012 5 s，配准性能优于其他三种对比算法，证明了本文算法的可行性。

4 结束语

针对ICP算法对点云配准过程中需要输入较好初值和收敛速度慢的问题，本文提出了一种融合PCA的改进ICP算法。首先利用PCA算法对点云数据进行处理实现两组点云主轴对齐，定义主轴基向量，利用主轴基向量间的关系实现了主轴方向的校正，获得点云配准的初始位姿。对比FPFH、4PCS、PFH算法，本文粗配准算法所用时间分别提高了20.2%、50.5%、44.4%，配准精度分别提高了66.9%、48.5%、79.4%。在部分重叠区域的点云配准中，粗配准为精配准提供了较好的初值，本文提出一种利用重叠区域的有效点对进行ICP配准算法，通过计算有效点对中欧式距离较大的点对来求解最优变换参数，完成精配准。通过在Bunny点云和支座点云配准的实验表明，在重叠度较低和初始位置相差较大的情况下，本文算法在收敛精度和配准时间上都优于对比算法，同时弥补了传统ICP算法收敛速度慢的不足，并为ICP算法提供了较好初值。但文本算法在点云较稠密或点云数量较多时，配准误差较大，之后将着重于研究大数据点云的配准准确性。