高效UKF相位解缠算法

刘媛媛，谢先明，田宪辉，李春，曾庆宁

(1.桂林电子科技大学 信息与通信学院，广西 桂林 541004；2.广西科技大学 电气与信息工程学院，广西 柳州 545006)

0 引言

相位解缠是干涉合成孔径雷达测量(interferometric synthetic aperture radar，InSAR)、光学干涉测量、合成孔径声呐(interferometric synthetic aperture sonar，InSAS)以及核磁共振成像等数据处理过程中的重要步骤之一[1]。由于三角函数的周期性，从干涉测量中获取的表征目标参数的干涉相位被限制在其相位主值(-π，π]区间，俗称缠绕相位；从缠绕相位中恢复反应目标参数的真实干涉相位，即为所谓的相位解缠[2]。在理想情况下，通过对缠绕相位加上2π的整数倍即可实现相位解缠。然而，干涉测量过程中的相位跳变、相位噪声、雷达阴影等干扰因素均会显著增加相位解缠的难度，为此研究者们相继提出了各种各样方法，来解决干涉图的相位解缠问题。

干涉图相位解缠算法研究至今大致可分为以下三类：路径跟踪法、最小范数法、基于非线性滤波的状态估计法。路径跟踪法重要代表有枝切法(branch-cut,BUT)[3]、质量引导法(quality guidance phase unwrapping，QGPU)[4]、网络流方法[5]等算法。枝切法通过识别残差点以及建立相应的枝切线，积分时避开枝切线来实现相位解缠，在干涉图相位噪声较小、残差点较少的情况下解缠速度快、精度高。然而，当干涉图噪声过大、残差点较多且分布较密集时，会产生“孤岛”现象。质量引导法则是在相位质量图的指导下沿高质量到低质量像元的积分路径进行解缠，在相位噪声较小时可获得较为稳健的解缠结果；而当干涉图相位噪声较大时，相位解缠过程中的误差将难以避免地沿着解缠路径传递，从而降低相位解缠精度。网络流算法的典型代表为最小费用流算法，该算法将相位解缠问题转化为网络费用最小化问题，通常能从干涉相位噪声较小的干涉图中获得较为稳健的相位解缠结果，但当干涉图信噪比较低或相位残差点较多时，该方法相位解缠精度与效率下降严重。最小范数法中的典型代表有基于快速傅里叶变换的无权重最小二乘法[6]、加权最小二乘法[7]等算法。这类方法将相位解缠问题转换成了数学上的最小范数问题，通过在缠绕相位微分与解缠相位微分之间建立合适代价函数来求解解缠相位的估计值，这类方法通常能连续与平滑地解缠相位，但易降低解缠相位的动态范围，导致干涉图条纹细节信息失真严重。基于非线性滤波的状态估计法因其特有的抗相位噪声能力而引起人们越来越多的关注，这类方法降低了干涉图前置滤波对相位解缠的限制，包括扩展卡尔曼滤波相位解缠算法[8-9]、无味卡尔曼滤波相位解缠算法(unscented Kalman filter phase unwrapping，UKFPU)[10-11]，以及粒子滤波类相位解缠算法[12-13]。其中，无味卡尔曼滤波相位解缠算法使用基于无味变换的sigma点来捕获状态变量的均值和方差，能够减少非线性系统模型线性化造成的相位信息丢失，且利用路径跟踪策略来指导相位解缠程序沿高质量区域到低质量区域解缠干涉图，在许多干涉图相位解缠实例中都获得了较好的解缠结果。然而该相位解缠算法需要在相位解缠过程不断地搜索最佳待解缠像元，其时间耗费较大，不利于实时性要求较高的一些应用场景，因此如何保持相位解缠精度(亦或是提高相位解缠精度)的同时提高解缠效率成为亟待解决的问题。Xie等[14]提出一种改进的无味卡尔曼滤波相位解缠算法，是将量化路径引导策略、基于相位质量信息的像素分类策略与无味卡尔曼滤波相结合的结果，多种干涉图相位解缠实例表明该方法在保持较好解缠精度的同时解缠效率有所提升；Xie[15]提出一种迭代无味卡尔曼滤波相位解缠算法，是将迭代无味卡尔曼滤波器、基于修正矩阵束的相位梯度估计器和基于堆排序的高效质量引导策略相结合的结果，干涉图相位解缠实例表明该方法相位解缠精度以及解缠效率都有所提升。除上述相位解缠方法外，最近有一些基于可靠性掩模的加权最小二乘相位解缠算法[16]、相位解缠的CKF(cubature Kalman filter，CKF)局部多项式系数递推估计法[17]、深度学习算法[18-19]被提出对干涉图进行相位解缠，这些方法通常是有效的，在一些干涉图相位解缠实例中获得了较好的解缠结果，这些方法有利于拓展相位解缠技术的应用领域。

把可靠性掩模图、像元扩散策略以及无味卡尔曼滤波算法结合起来，本文提出一种高效UKF相位解缠算法。首先，根据干涉图生成相应的枝切线分布图；其次，利用二阶差分函数计算干涉图中各像元的质量权值，并设置阈值将质量权值二值化为“0”和“1”；再次，由枝切线分布图以及二值化质量权值矩阵生成可靠性掩模图，该可靠性掩模图将干涉图分为权值为“1”的高质量像元(非枝切线上的二值化质量权值为“1”的像元)、权值为“0”的低质量像元(枝切线上的像元、二值化质量权值为“0”的像元以及枝切线围成的闭环区域中的像元)两部分；然后，由可靠性掩模图确定解缠路径，先利用UKF相位解缠程序按照像元扩散策略解缠高质量像元，余下未解缠像元根据已解缠像元信息，利用UKF相位解缠程序按照行(或列)的方式进行解缠。实验结果表明，高效UKF相位解缠算法能够高效与稳健地处理干涉图的相位解缠问题。

1 UKF相位解缠程序方法和技术流程

利用干涉图相邻像元干涉相位之间的关系，干涉图相位解缠系统方程可参见文献[11]。文献[11]提出的无味卡尔曼滤波相位解缠算法是UKF相位解缠程序与路径跟踪策略相结合的结果。无味卡尔曼滤波相位解缠算法利用路径跟踪策略来指导UKF相位解缠程序沿高质量区域到低质量区域解缠干涉图，具有较高相位解缠精度的同时时间耗费较大。

2 高效UKF相位解缠算法

把可靠性掩模图、像元扩散策略以及无味卡尔曼滤波算法相结合，本文提出一种高效UKF相位解缠算法。该方法主要包括以下4个步骤。

步骤1：根据枝切线生成原理生成干涉图的枝切线分布图。

1)识别干涉图中的残差点，利用最小回路积分进行判断并标记位置，生成残差点矩阵。

2)按照从左至右、从上至下的原则，以搜索到的第一个残差点为中心。

3)首先在3×3的窗口中搜索其他残差点，如果搜索到极性相反的点，连接两点生成枝切线，并标记该枝切线极性为0。

4)如果搜索到极性相同的点，连接两点生成枝切线，并将极性值标记为该枝切线极性值，并以当前的残差点为中心继续搜索。

5)若在邻域内没有搜索到残差点，则扩大搜索范围为5×5、7×7、……，直到图像边界，连接最近的边界点，生成枝切线。

6)重复以上过程，直至枝切线连接并平衡所有残差点为止。值得注意的是，在残差点连接过程中，已达到“电荷”平衡的残差点不用重复连接，可减少枝切线数量。

步骤2：利用二阶差分函数计算干涉图中各像元的权值[16]，并设置阈值将该权值二值化为“0”和“1”，0表示低质量像元，1表示高质量像元。

(1)

(2)

式中：W为缠绕算子，将相位差值限制于(-π，π]之间；φi，j表示干涉图(i，j)像元缠绕相位；Ri，j表示(i，j)像元的可信度。二值化质量权值表示如式(3)所示。

(3)

式中：θ表示可信度阈值；qi，j表示(i，j)像元二值化质量权值。

步骤3：由枝切线分布图以及干涉图二值化质量权值矩阵生成可靠性掩模图，非枝切线上的二值化质量权值为“1”的像元为权值为“1”的高质量像元，枝切线上的像元、二值化质量权值为“0”的像元以及枝切线围成的闭环区域中的像元等像元为权值为“0”的低质量像元。

步骤4：把可靠性掩模图、像元扩散策略以及UKF相位解缠程序结合起来，按以下步骤对干涉图进行解缠。

1)首先选取非枝切线上可信度最高的像元为起点，其缠绕相位作为解缠相位估计值，其估计误差方差预设为0.6；利用UKF相位解缠程序解缠4个邻接像元中的高质量像元，随后将已解缠像元邻接像元中的未解缠高质量像元依次存储在“邻接列”中。

2)按顺序取出“邻接列”中的待解缠像元，利用UKF相位解缠程序对该像元进行解缠，随后将解缠像元邻接像元中的未解缠高质量像元依次存储在“邻接列”中。

3)若“邻接列”不为空，回到步骤2)，若为空，则转步骤4)。

4)根据已解缠像元信息，利用UKF相位解缠程序按行(或列)的方式逐一解缠余下的未解缠像元。

图1进一步给出了本文算法解缠步骤示意图。图1(a)中“黄色”像元(非枝切线上可信度最高的像元)为起始像元，“绿色”像元为高质量像元，“红色”像元为低质量像元，先利用UKF相位解缠程序进行解缠“绿色”像元；“红色”像元将在步骤4)中进行解缠。图1(b)给出了执行步骤1)之后的结果，其中，“黑色”像元为已解缠像元，“蓝色”像元为存储在“邻接列”的待解缠像元，其余像元为未处理的像元。需要注意的是，若干涉图条纹十分密集，无法利用UKF相位解缠程序从选择的起点进行解缠时，可以选择可信度次高的像元为起点，按照图1(b)方式进行解缠。

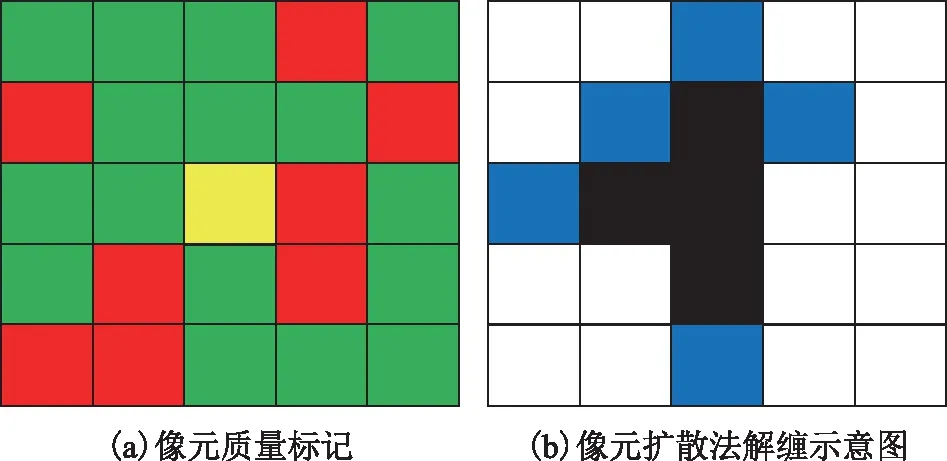
图1 像元扩散法解缠示意图

3 实验结果与分析

为了验证本文算法性能，利用不同算法包括BUT、非加权迭代最小二乘法(unweighted iterative least squares，ILS)、QGPU、UKFPU，以及本文算法，在同一MATLAB软件环境(Intel i7-6700U@3.40 GB CPU+8 GB RAM)下解缠不同的模拟干涉图和实测干涉图，并对各算法解缠结果进行比较分析。

3.1 模拟数据实验

图2为两幅不同模拟干涉图(256像素×256像素)。图3(a)～图3(b)分别为图2(a)～图2(b)含噪声的缠绕相位图，其信噪比依次为3.01 dB、2.18 dB。依次用BUT、ILS、QGPU、UKFPU以及本文算法对上述两幅干涉图进行解缠，解缠结果分别如图4～图8、图9～图13所示。

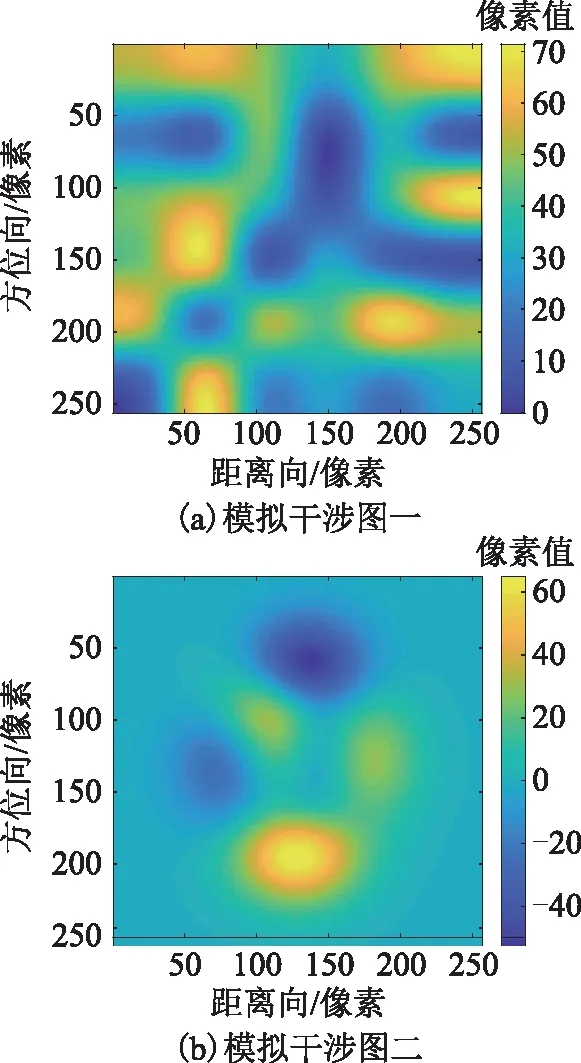
图2 模拟干涉图

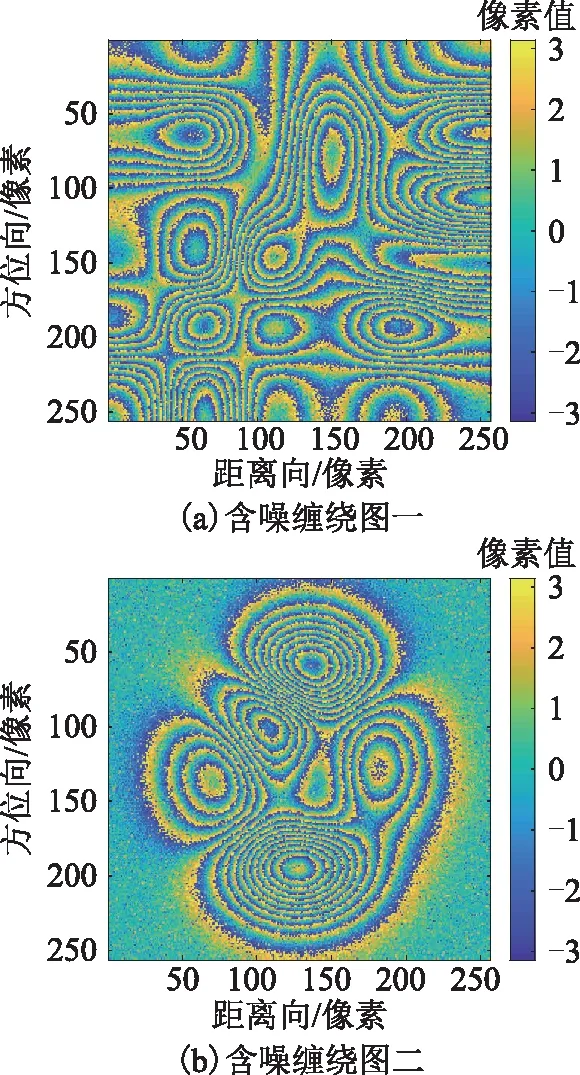
图3 含噪缠绕相位图

图4 BUT算法解缠相关处理结果

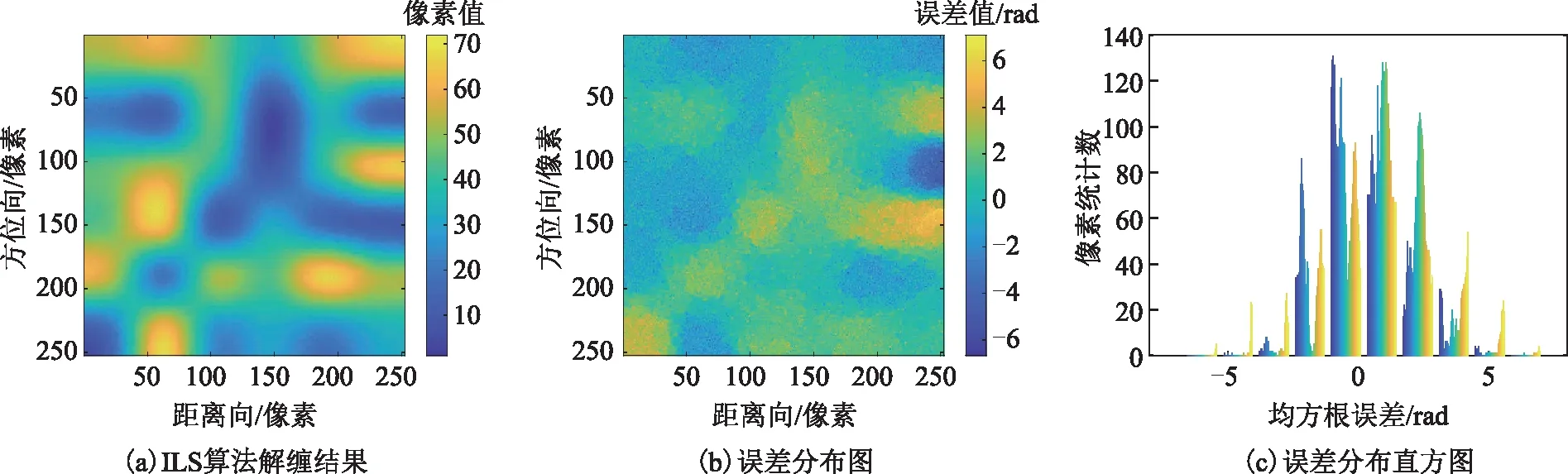
图5 ILS算法解缠结果

图6 QGPU算法解缠结果

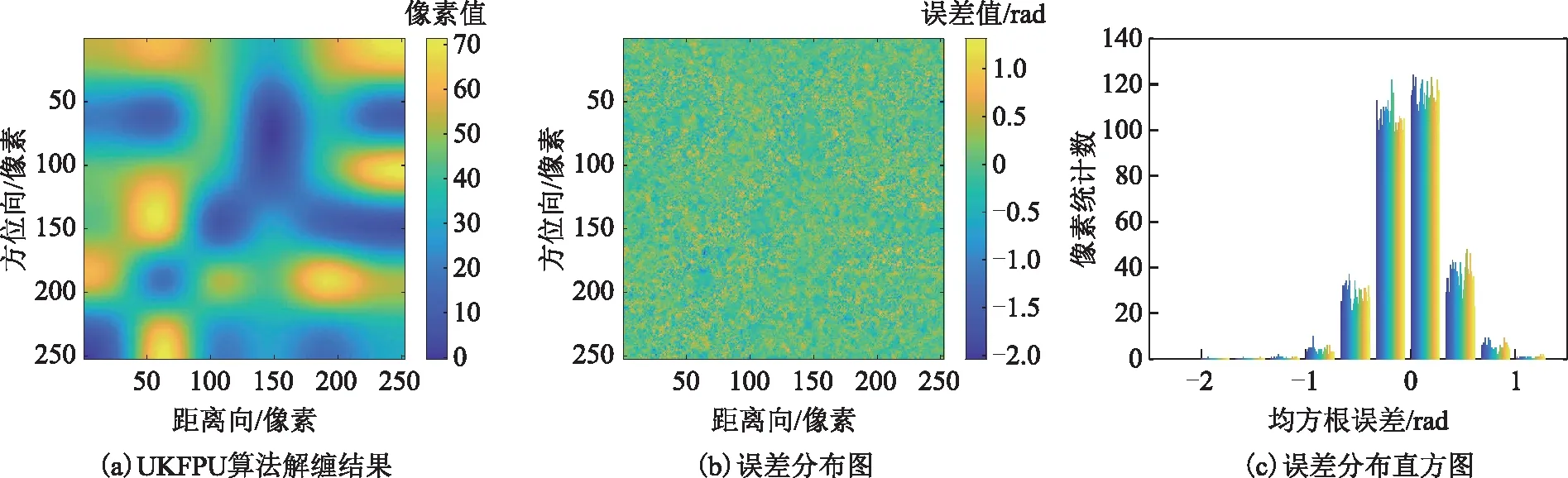
图7 UKFPU算法解缠结果

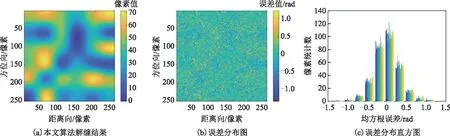
图8 本文算法解缠结果

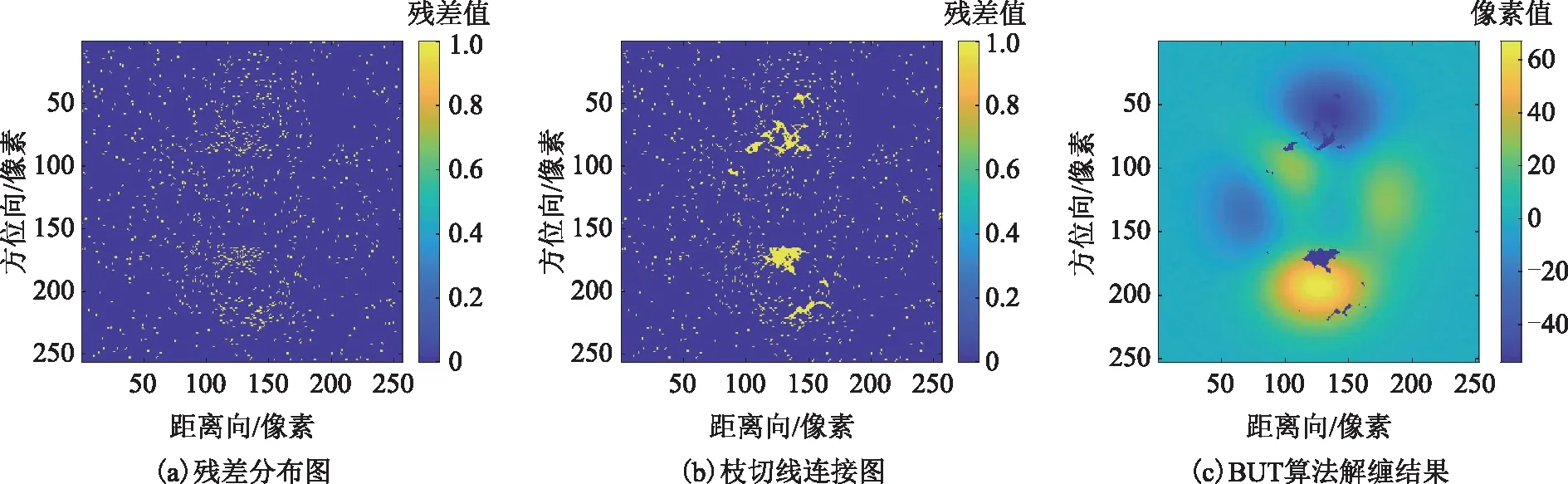
图9 BUT算法解缠相关处理结果

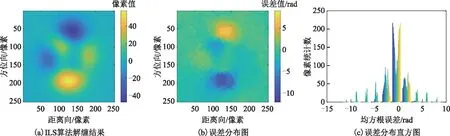
图10 ILS算法解缠结果

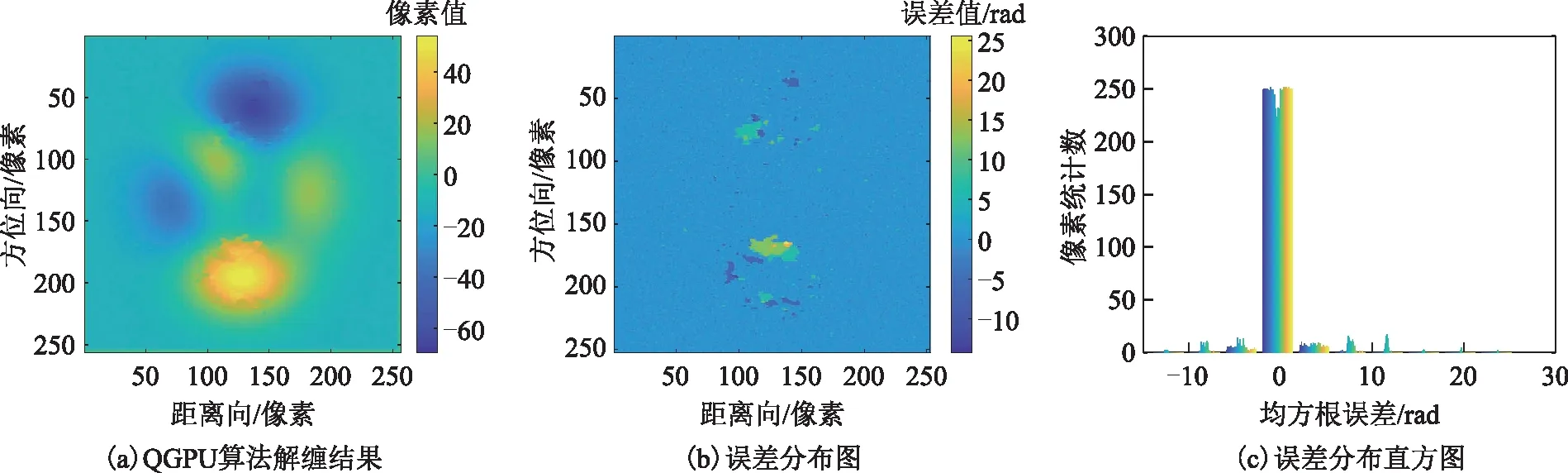
图11 QGPU算法解缠结果

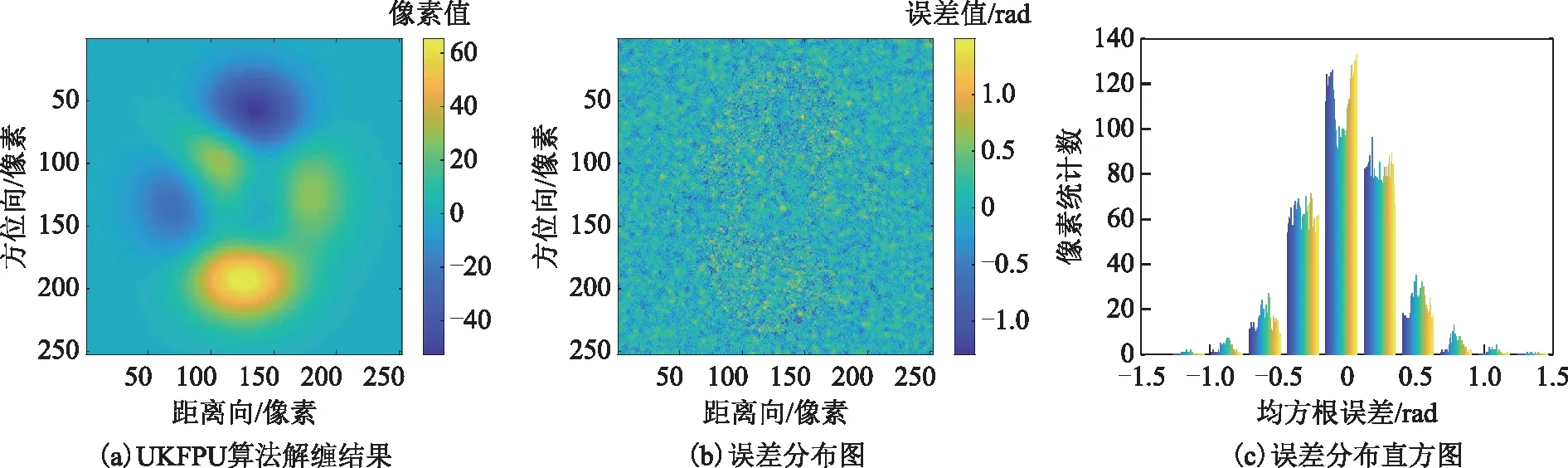
图12 UKFPU算法解缠结果

图13 本文算法解缠结果

图4、图9第一行从左至右分别代表图3(a)～图3(b)的缠绕相位图的残差点、枝切线、枝切法解缠结果，图5～图8、图10～图13的左列、中间列和右列分别表示ILS、QGPU、UKFPU、本文算法解缠相位结果、解缠相位误差和解缠相位误差直方图。表1为各算法解缠不同信噪比干涉图的均方根误差。表1中的“-”表示随着噪声增大，枝切法形成一些闭环区域，这些闭环区域无法解缠，因此无法统计均方根误差。由图4～图8及图9～图13可以看出：由于干涉图信噪比较低，BUT算法解缠相位中存在部分无法解缠的区域；ILS算法虽然解缠结果较为平滑，由其解缠相位误差图、解缠相位误差直方图以及表1可知其解缠误差较大；QGPU算法解缠过程中误差沿着积分路径传递，导致部分区域误差较大；而UKFPU以及本文算法相较于BUT、ILS、QGPU算法具有更稳健的相位解缠能力，且UKFPU与本文算法解缠精度相当。表2列出了上述算法解缠上述干涉图的平均运行时间。可以看出，本文算法解缠时间远小于QGPU、UKFPU算法。因此，本文算法在保持稳健的相位解缠能力的同时，其时间消耗亦是可以接受的。

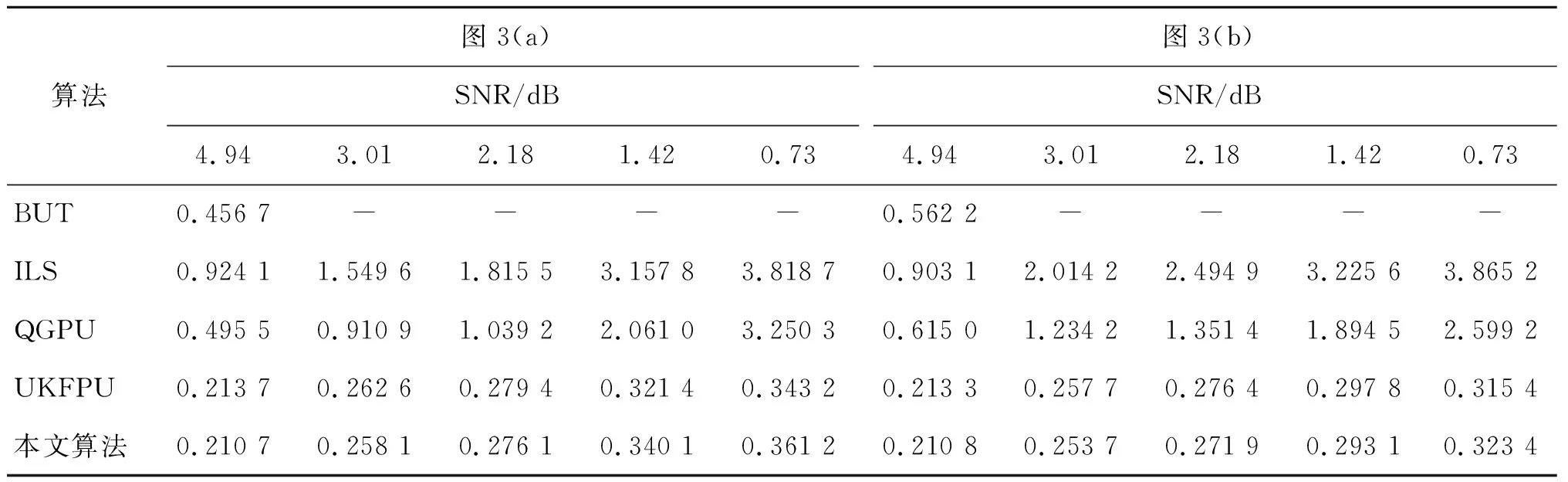
表1 不同信噪比下不同算法均方根误差

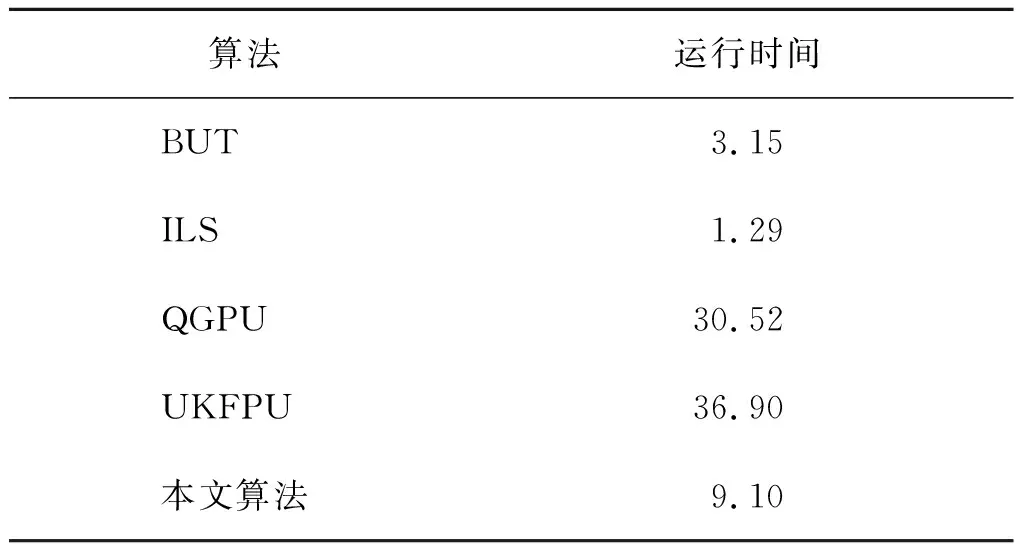
表2 各算法解缠时间 s

3.2 实测数据实验

图14为经中值滤波处理过后截取的部分Enta火山干涉图，各算法解缠结果如图15所示，其解缠相位重缠绕结果如图16所示。

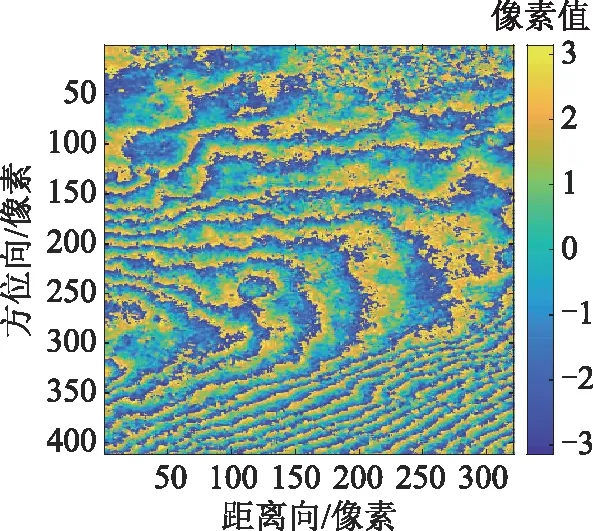
图14 局部Enta火山干涉图

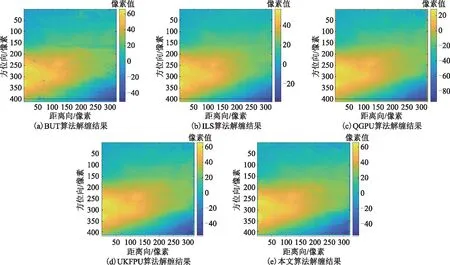
图15 各算法解缠结果

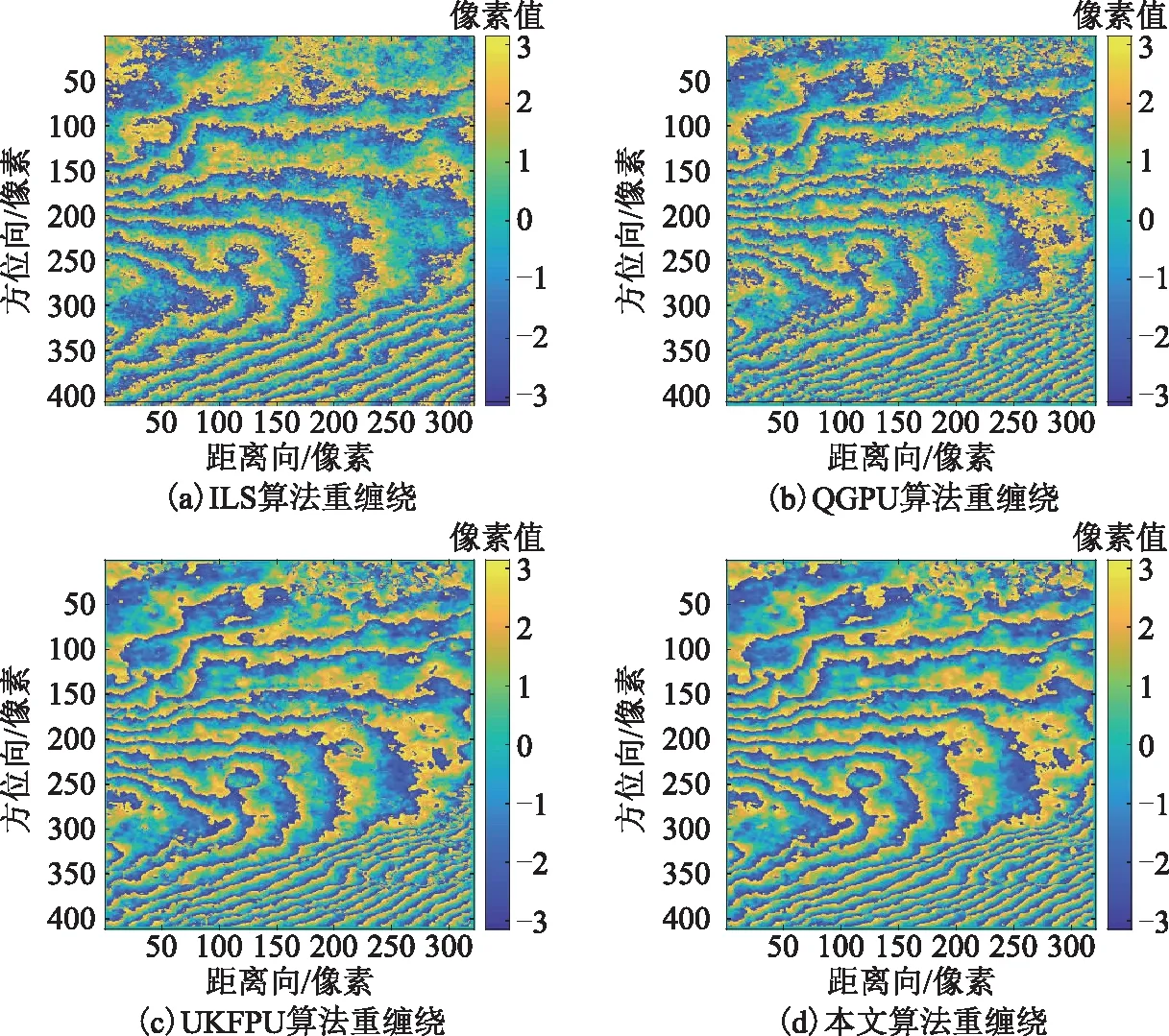
图16 各算法解缠相位重缠绕结果

图17为三峡实测干涉图，各算法解缠结果如图18所示，解缠相位重缠绕结果如图19所示。

由图15(a)以及图18(a)可以看出，BUT算法解缠相位图存在部分无法解缠以及明显不一致的区域。由图15(b)以及图18(b)可见，ILS算法解缠结果较为光滑，但根据图16(a)以及图19(a)可以发现，ILS算法重缠绕结果相较于图14以及图17原始干涉图条纹差别较大，大量干涉条纹细节信息丢

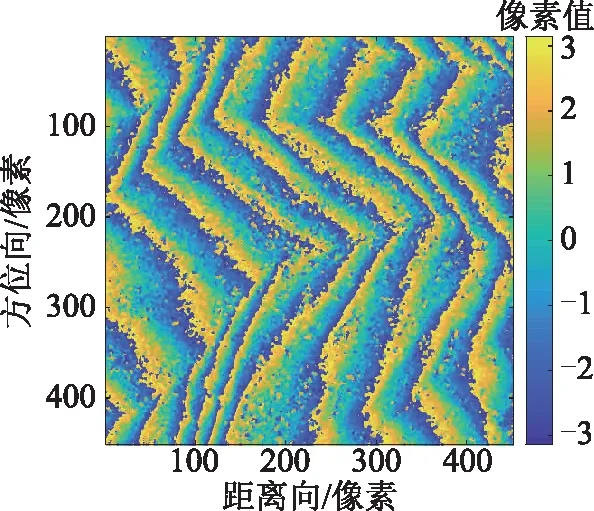
图17 三峡实测干涉图

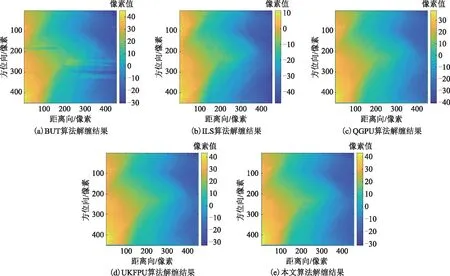
图18 各算法解缠结果

图19 各算法解缠相位重缠绕结果

失，故该方法解缠结果精度有限。而由图15(c)～图15(e)以及图18(c)～图18(e)可知，QGPU、UKFPU、本文算法解缠结果较好，且由图16(b)～图16(d)以及图19(b)～图19(d)可见，其重缠绕干涉图条纹与原始干涉图条纹基本一致。与此同时，不同于QGPU算法，UKFPU算法以及本文算法重缠绕相位图中残留散斑噪声较少，这表明这两种算法能在相位解缠的同时有效去除干涉图中相位噪声，有利于获得更高的解缠精度。表3给出了上述算法的运行时间，可知本文算法解缠时间远小于QGPU、UKFPU算法。

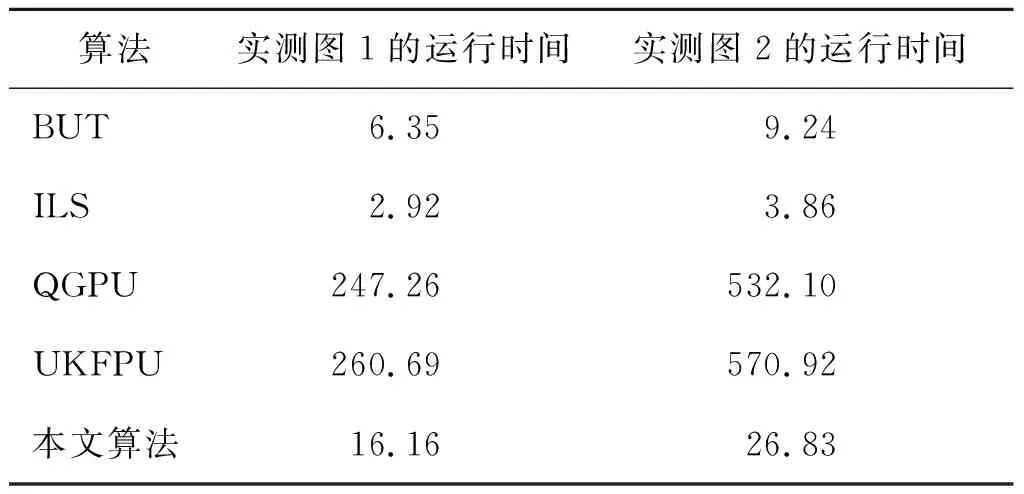
表3 各算法解缠时间 s

4 结束语

本文提出一种高效UKF相位解缠算法，该算法是可靠性掩模图、像元扩散策略以及无味卡尔曼滤波算法相结合的结果。模拟数据实验以及实测数据实验结果证明了高效UKF相位解缠算法有效性，相对于传统算法如BUT、ILS以及QGPU，具有更稳健的相位解缠能力，且在时间耗费较少的同时其解缠精度与UKFPU算法相当。然而，所提出的方法处理复杂地形仍有改进空间，且相位解缠时间消耗还有优化的空间。努力寻找高效稳健的相位解缠技术是我们未来努力的目标。