稀疏表示噪声抑制算法提升BOTDR系统信噪比的研究*

崔 宁刘 丽王清琳白 清王 宇刘 盺靳宝全*

(1.太原理工大学新型传感器与智能控制教育部与山西省重点实验室，山西 太原 030024；2.山西省交通科技研发有限公司，山西 太原 030024)

布里渊光时域反射仪(Brillouin optical time domain reflectometer，BOTDR)[1]是一种分布式光纤传感系统，其原理是利用光纤自身性质随周围环境改变进行温度或应变测量[2-3]。因其单端注入、抗电磁干扰[4]等优点，近些年来广泛应用于灾害预警、安全监测等众多领域中[5-7]。然而，系统单端泵浦、探测自发后向散射光的特性使光纤中的信号较为微弱。而实际工程应用中系统常铺设于野外环境恶劣的地区也会对信噪比造成严重的损耗。因此信噪比成为限制BOTDR系统整体性能的重要因素。

在布里渊系统的信噪比提升领域，传统的方法有累加平均，小波去噪，脉冲编码等。1985年，Dakin等在拉曼光时域反射仪(Raman optical time domain reflectometer，ROTDR)的实验中对系统施加了400000次平均，有效消除了数据中的高斯噪声；2016年，电子科技大学的王子南等[8]采用基于BayesShrink的离散小波算法提升了布里渊光时域分 析 仪(Brillouin optical time domain analyzer，BOTDA)系统的信噪比并降低了系统的测量不确定度；2018年，华中科技大学的唐明团队[9]将信道估计算法与互补编码相结合，提高了BOTDR系统的信噪比并降低了测量的不确定度。以上方法均能有效提升系统的信噪比，但会一定程度上对系统的实时性造成影响，并且上述方法对信号在多维域(时域、频域、距离域)的冗余性和相关性没有做到很好的利用，限制了其信噪比的提升能力[10]。

近些年来，国内外许多专家学者提出在分布式光纤传感领域引入数字图像处理算法[11]，利用测得数据在空间域的相关性进行噪声抑制工作。2013年，Zhu等人[12]利用数字图像处理领域的二维边缘检测方法，实现了8.4 dB的信噪比提升。2016年，瑞士洛桑联邦理工学院的Soto团队[13]使用图像处理领域的非局部均值算法，在拉曼分布式传感领域获得了13.6 dB的信噪比提升。以上方法都实现了信噪比提升，验证了使用数字图像处理算法进行信噪比提升的有效性。为BOTDR系统中的噪声抑制工作提供了传统去噪算法之外的思路。

在本文中将三维布里渊增益谱(Three dimensional Brillouin gain spectrum，3D-BGS)中的某点与数字图像中的一个像素点进行对应，提出基于稀疏表示的BOTDR系统信噪比提升算法。利用高斯白噪声随机而无法被复现的特性，以重构信号为手段分离噪声，进而提升系统的信噪比。经过对算法的仿真分析可得，该方法可以有效提升BOTDR系统的信噪比，当添加10 dBm噪声时，信噪比可提升5.26 dB。

1 降噪原理

1.1 稀疏表示基本原理

由稀疏表示[14-16]的理论可知，有效信号具有不同于噪声的内在规律性，能够被字典中部分原子的线性组合稀疏表达(在本文中，将BOTDR系统中采集得到的3D-BGS视为有效频移信息和随机噪声的组合)。

在BOTDR系统布里渊增益谱(Brillouin gain spectrum，BGS)的测量过程中，对于不同位置BGS的测量是相似的，仅在周围环境中温度或应变信息发生改变时局部中心频率发生改变。因此将BGS曲线叠加后，3D-BGS矩阵具有相似性及冗余性，利用这些性质，能够做到对信号的稀疏表示。而系统的电域链路在光电转换及后续放大过程中引入的热噪声及散粒噪声属于高斯白噪声，具有随机性，无法被字典原子稀疏表示。因此在信号重构的过程中，3D-BGS矩阵能够被字典原子的线性组合稀疏表示，而电域链路引入的高斯白噪声信号在矩阵重构的过程中作为原始3D-BGS与重构信号之间的残差丢弃，从而达到分离噪声，提升系统信噪比的目的。

稀疏表示的基本原理如图1所示。在图1中使用色块矩阵表示文中待进行降噪处理的3D-BGS，色块对应数字，颜色越浅对应数值越小，白色块对应数值为0。图1中使用矩阵Y∈Rm×n表示测得的3DBGS，其中m对应不同的频率，n对应沿光纤的不同距离，y i(i＝1，2，…，n)对应三维BGS矩阵Y的某一列向量，即沿光纤某位置处的BGS曲线；D∈Rm×m对应设计生成的字典矩阵，di(i＝1，2，…，m)表示字典的列向量；X∈Rm×n表示提取的系数矩阵，xi(i＝1，2，…，m)表示系数矩阵的行向量。选取字典中的列向量进行线性组合，即可完成对矩阵Y中对应列y i的重构。沿光纤逐点完成对BGS的重构，即完成了对整个3D-BGS的重构去噪工作。

图1 稀疏表示基本原理

可由图1提取使用稀疏表示进行降噪的优化目标:在足够稀疏的前提下，为满足重构精确性的同时进行降噪处理。

数学化上述过程即为:

式(1)由两部分组成，左式中ε指迭代过程中的目标误差，‖·‖2指l2范数，左式保证了重构BGS的精确度。右式中xi(i＝1，2，…，m)指系数矩阵的行向量，‖·‖0指l0范数。l0范数能够保证系数向量的稀疏度。因此求解式(1)就能得到对原始3D-BGS满足稀疏性、精确性及噪声抑制需求的重构。式(1)中有2个变量D、xi需要优化求解，这里采取固定其中一个交替优化的方式反复迭代，直到达到目标阈值。

1.2 算法流程

稀疏表示算法的具体流程如图2所示。

①建立离散余弦变换(Discrete cosine transform，DCT)初始字典D0。如图2(a)(Ⅰ)所示，输入原始3D-BGS矩阵Y，固定字典D0，利用正交匹配追踪(Orthogonal matching pursuit，OMP)算法[17]求解，得到图(Ⅱ)中的初始系数矩阵X0及残差；

图2 稀疏表示算法流程图

②如图2(b)所示，利用生成的系数矩阵及原始3D-BGS矩阵Y，使用K-奇异值分解(k-singular value decomposition，K-SVD)算法[18]逐列更新初始字典Dk及系数矩阵Xk，最终得到在一次迭代过程中更新完成的字典矩阵Dk+1及系数矩阵Xk+1。图2(Ⅰ)中di，xi为字典某次更新中待更新的列向量(i＝1，2，…，m)。该列更新完成后，即可得到图(Ⅱ)中。全部列向量更新完成后，即可得到图(Ⅲ)中更新完毕的字典矩阵Dk+1及系数矩阵Xk+1；

以上两步迭代反复交替进行，直到得到的结果满足目标阈值。图中Dk及Xk表示某次迭代过程中待更新的字典及系数矩阵。

③如图2(c)所示，利用迭代完成的字典及系数矩阵输出重构的3D-BGS。

2 仿真与结果分析

2.1 仿真数据构建

进行仿真实验对上述理论进行验证。在10.635 GHz~10.805 GHz的范围内以5 MHz为步进进行仿真扫频。设置模拟传感光纤总长度为10.15 km，中心频率为10.721 GHz。在9.156 km~9.295 km处将中心频率移动到10.752 GHz，设置模拟变温区，以模拟在外界环境发生变化时布里渊频移曲线(Brillouin frequency shift，BFS)发生的突变情况。仿真理想数据如图3所示。

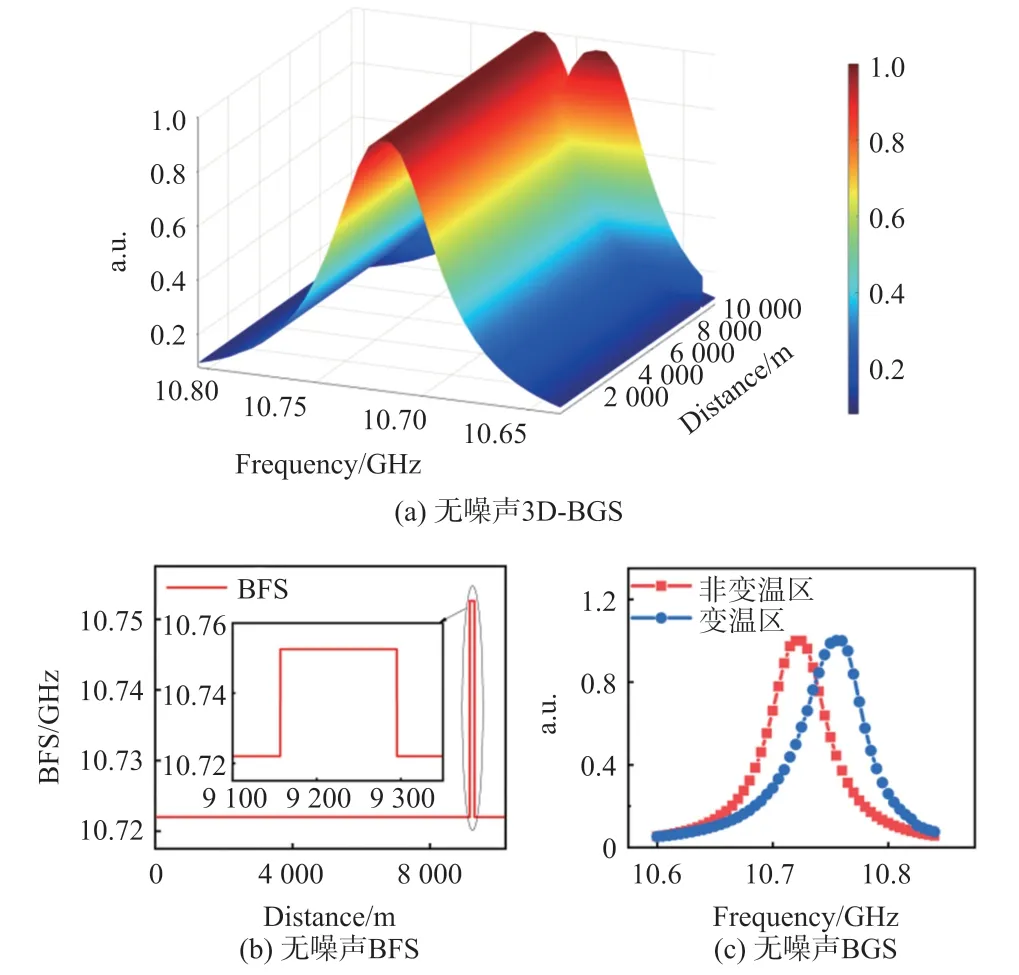
图3 无噪声理想数据

图3(a)为未添加噪声的理想3D-BGS。图3(b)为图3(a)中理想3D-BGS对应的全局BFS分布以及模拟变温区的局部放大图。从图3(b)中可以看出中心频率为10.721 GHz的模拟非变温区以及中心频率为10.752 GHz的模拟变温区；图3(c)为理想3D-BGS对应的单频BGS，其中左侧曲线表示非变温区的BGS，右侧曲线表示变温区某位置处的BGS，由图3(c)可以看出理想扫频数据在模拟变温区产生的频移。

BOTDR系统的电域链路在光电转换及后续放大过程中引入了高斯白噪声。在本文中，通过在无噪声理想数据中加入高斯白噪声对上述过程进行仿真模拟。

2.2 算法效果分析

在无噪理想数据中添加10 dBm的噪声，并应用稀疏表示算法进行去噪处理，降噪前后的3D-BGS如图4所示。

图4 噪声功率为10dBm时降噪前后3D-BGS对比

图4(a)为对图3(a)中理想3D-BGS数据添加10 dBm噪声的3D-BGS图；图4(b)为使用文中引用的稀疏表示去噪算法对图4(a)进行去噪处理后的3D-BGS图。由图4可得，经过算法处理，与图4(a)相比，图4(b)中的随机噪声明显减少，同时图中曲线平滑度得到了提升。由图4中降噪前后3D-BGS的对比可以验证稀疏表示算法的去噪能力。

将稀疏表示算法降噪处理前后变温区与非变温区的数据分别绘制单频BGS曲线。降噪前后的对比结果如图5所示。图5(a)表示算法处理前后非变温区的单频BGS；图5(b)表示算法处理前后变温区的单频BGS。从图5可以看到，经过算法处理，单频BGS曲线的波动情况得到明显抑制。因此可以从单频BGS的角度验证稀疏表示算法的降噪能力。

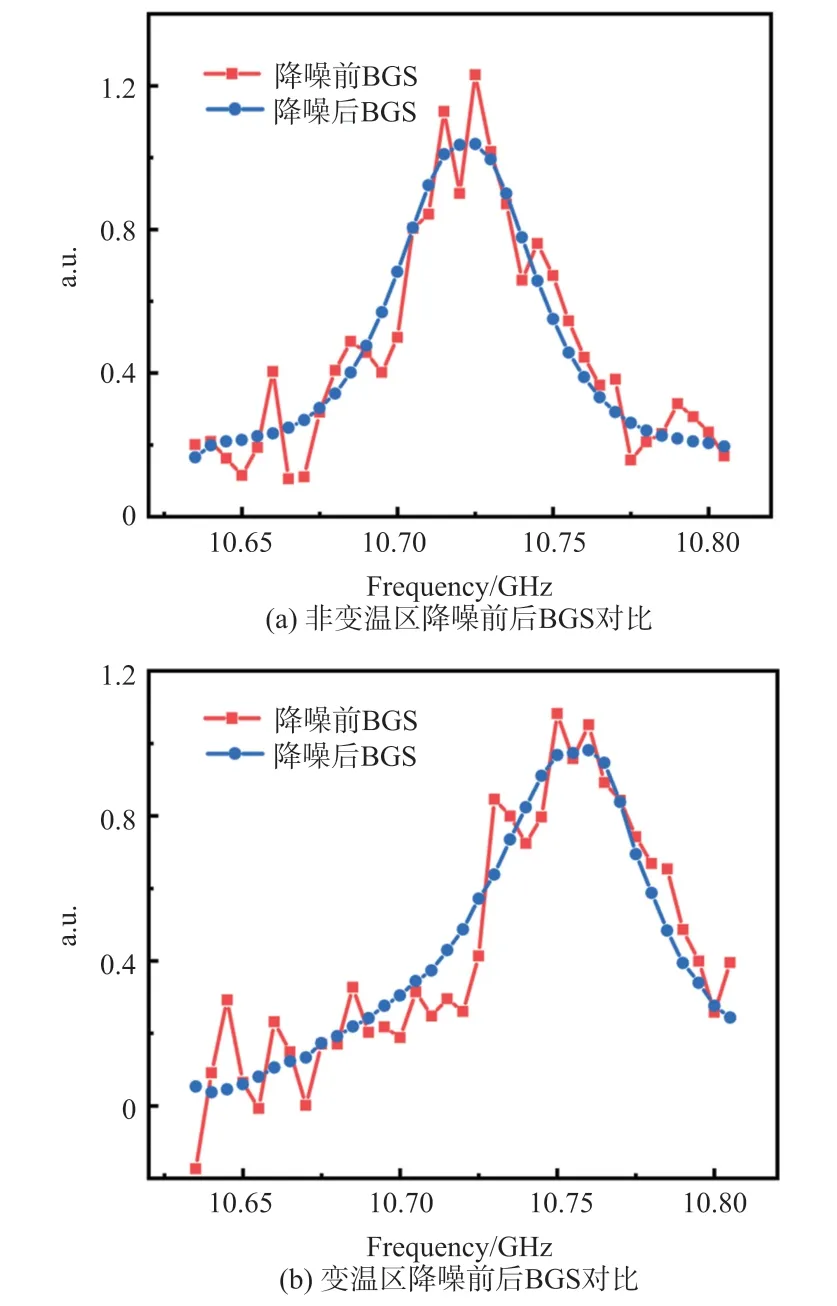
图5 降噪前后非变温区与变温区单频BGS对比

将稀疏表示算法降噪前后的3D-BGS分别提取BFS曲线进行对比，得到的降噪前后的BFS曲线及其局部放大图如图6所示。

由图6可得，经过稀疏表示算法进行降噪处理，整条BFS曲线的噪声波动均得到了有效抑制。可以看到，降噪前非变温区和变温区的均方根误差(Root mean square error，RMSE)分别为1.35 MHz和1.43 MHz，经过算法降噪进行处理，这两个部分的RMSE值分别降至0.404 MHz和0.395 MHz。由此可得，本文所引入的算法可以有效地降低3D-BGS中的随机噪声。

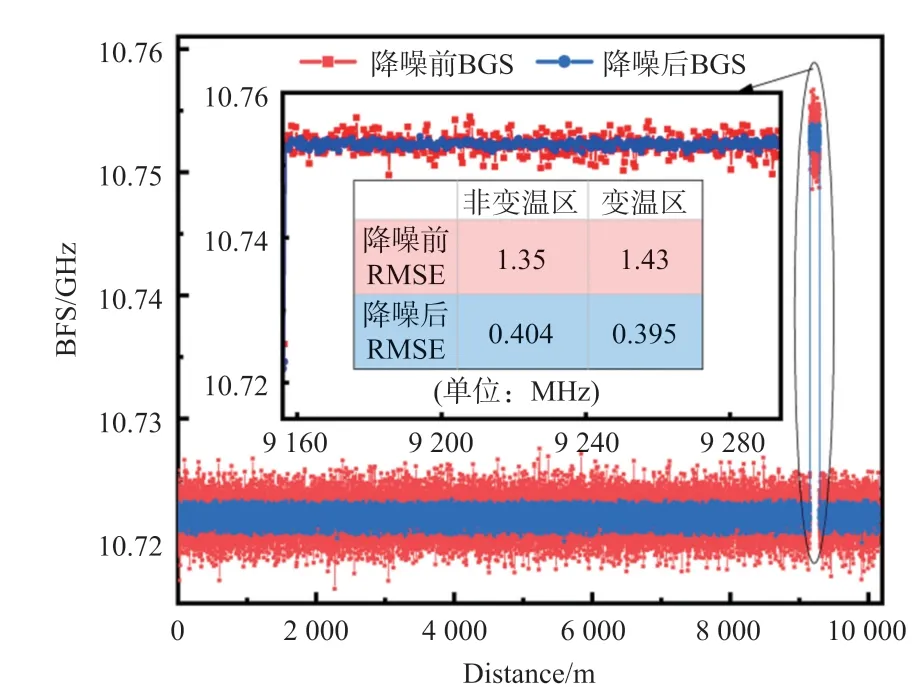
图6 降噪前后BFS曲线对比

对稀疏表示算法降噪处理前后的3D-BGS分别提取BFS曲线，并分组计算RMSE后，得到的结果如图7所示。

图7 降噪前后RMSE对比

将信号功率与噪声功率的比值定义为信噪比SNR，如式(2)所示:

式中:Ps为信号功率，PN为噪声功率。在降噪处理过程中信号功率不变，因此信噪比的提升SNRIm如式(3)所示:

式中:SNRBe和SNRAf分别为降噪前后的信噪比，PN-Be和PN-Af分别表示降噪前后的噪声功率，即为降噪前后BFS曲线计算RMSE的均值得到的结果，如图7所示。

由图7可得，降噪前后功率PN-Be和PN-Af分别为1.31 MHz和0.39 MHz，代入式(3)计算可得，本文算法对于信噪比的提升为5.26 dB。可以得出结论，本文提出的BOTDR去噪算法可以有效抑制3D-BGS中的噪声，提升数据的信噪比。

由图7可得，与算法处理前相比，3D-BGS谱的RMSE值有明显的下降。

3 实验结论与展望

本文将图像处理领域的稀疏表示算法应用于BOTDR系统进行噪声抑制研究。利用3D-BGS信号自身存在的冗余性和相关性对信号进行了稀疏表示，由于高斯噪声的随机性，在信号重构过程中作为残差丢弃，因此可以有效降低随机噪声。文中基于稀疏表示去噪算法建立了3D-BGS仿真模型，进行了算法去噪性能验证仿真分析。当高斯噪声为10 dBm时，能够实现5.26 dB的信噪比提升。研究证明，稀疏表示算法为应用图像处理方法提高BOTDR系统信噪比供了新的思路及理论依据。

此外，本文仅针对BOTDR信号处理中的随机噪声进行了降噪模拟分析。在实际实验中，BOTDR系统仍存在其他噪声。如何提取这部分噪声的数据特征，并对降噪算法做出针对性优化，进而提升系统的信噪比，是下一步的工作重点。